Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T05:00:21.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic properties of the equilibrium probability of identity in a geographically structured population

Published online by Cambridge University Press:  01 July 2016

Stanley Sawyer
Stanley Sawyer*
Affiliation:
Yeshiva University, New York
Get access Rights & Permissions [Opens in a new window]

Abstract

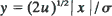Let I(x, u) be the probability that two genes found a vector distance x apart are the same type in an infinite-allele selectively-neutral migration model with mutation rate u. The creatures involved inhabit an infinite of colonies, are diploid and are held at N per colony. Set in one dimension and 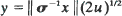in higher dimensions, where σ2 is the covariance matrix of the migration law (which is assumed to have finite fifth moments). Then 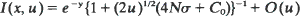in one dimension, 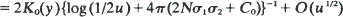in two dimensions, and 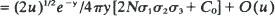in three dimensions uniformly for 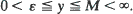Here C0 is a constant depending on the migration law, K0(y) is the Bessel function of the second kind of order zero, and 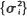are the eigenvalues of σ2. For symmetric nearest-neighbor migrations, 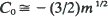in one dimension and 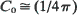log mi in two. For 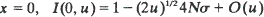is known in one dimension and C0 does not appear. In two dimensions, 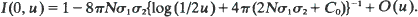These results extend and make more precise earlier work of Malécot, Weiss and Kimura and Nagylaki.

Keywords

MIGRATIONSTEPPING-STONE MODELPOPULATION STRUCTUREPOPULATION GENETICSSELECTIVE NEUTRALITY
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 2 , June 1977 , pp. 268 - 282
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cavalli-Sforza, L. and Bodmer, W. (1971) The Genetics of Human Populations. W. H. Freeman, San Francisco.Google Scholar
Fleming, W. and Su, C. (1974) Some one-dimensional migration models in population genetics theory. Theoret. Pop. Biol. 5, 431–449.Google Scholar
Kimura, M. and Ohta, T. (1971) Theoretical Aspects of Population Genetics. Monographs in Population Biology 4, Princeton University Press, Princeton, N.J. Google Scholar
Kimura, M. and Weiss, G. (1964) The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 49, 561–576.Google Scholar
Magnus, W., Oberhettinger, F. and Soni, R. (1966) Formulas and Theorems for the Special Functions of Mathematical Physics. Grundlehren der Math. Wiss. 52, Springer-Verlag, New York.Google Scholar
Malécot, G. (1948) Mathématiques de l'Hérédité. Masson, Paris. English translation with added appendix: The Mathematics of Heredity (1969), W. H. Freeman, San Francisco.Google Scholar
Malécot, G. (1959) Les modèles stochastiques en génétique de population. Publ. Inst. Statist. Univ. Paris. 8, 173–210.Google Scholar
Malécot, G. (1967) Identical loci and relationship. Proc. 5th Berkeley Symp. Math. Stat. Prob. 4, 317–332.Google Scholar
Malécot, G. (1976) Heterozygosity and relationship in regularly subdivided populations. Theoret. Pop. Biol. 8, 212–241.CrossRefGoogle Scholar
Maruyama, T. (1972) The rate of decrease of genetic variability in a two-dimensional population of finite size. Genetics 70, 639–651. See also other papers cited in his bibliography.Google Scholar
Nagylaki, T. (1974a) The decay of genetic variability in geographically structured populations. Proc. Natn. Acad. Sci. U.S.A. 71, 2932–2936.Google Scholar
Nagylaki, T. (1974b) Genetic structure of a population occupying a circular habitat. Genetics 78, 777–790.Google Scholar
Nagylaki, T. (1976a) The relation between distant individuals in geographically structured populations. Math. Biosci. 28, 73–80.Google Scholar
Nagylaki, T. (1976b) The geographic structure of populations. MAA Studies in Mathematical Biology, to appear.Google Scholar
Sawyer, S. (1975) An application of branching random fields to genetics. Probabilistic methods in differential equations. In Springer Lecture Notes in Mathematics 451, 100–112, Springer-Verlag, New York.Google Scholar
Sawyer, S. (1976a) Results for the Stepping Stone model for migration in population genetics. Ann. Prob. 4, 699–728.Google Scholar
Sawyer, S. (1976b) Branching diffusion processes in population genetics. Adv. Appl. Prob. 8, 659–689.Google Scholar
Sawyer, S. (1977) Rates of consolidation in a selectively neutral migration model. Ann. Prob. To appear.Google Scholar
Spitzer, F. (1964) Principles of Random Walk. Van Nostrand, New York.Google Scholar
Weiss, G. and Kimura, M. (1965) A mathematical analysis of the stepping stone model of genetic correlation. J. Appl. Prob. 2, 129–149.Google Scholar
Yasuda, N. (1975) The random walk model of human migration. Theoretic. Pop. Biol. 7, 156–167.Google Scholar