Article contents
Effects of blowing upon dynamic stability of blunt nosed re entry vehicles pitching in hypersonic flow
Published online by Cambridge University Press: 22 August 2023
Abstract
Blowing is often used to alleviate the intense heating rates on blunt noses of hypersonic vehicles. This flow efflux at the leading edge transforms the flow field in the blunt-nose regions with implications on the dynamic stability of the vehicles. As a demonstrative exercise, the flow fields past blunt-nosed and truncated-nosed conical bodies under blowing and no-blowing conditions were perturbed to obtain the unsteady effects using the shock expansion method to recover the unsteady pressure coefficient. Static and pitching moment derivatives were then duly obtained by integrating the differential of the unsteady pressure coefficient with respect to the pitch angle (α) or the pitch rate (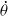 $\dot \theta $) together with the moment arm with reference to the centre of gravity. The results obtained for blunt-nose and truncated conical bodies show a noticeable drop in dynamic stability. Even when the flow is transformed from a tangential blowing at the shoulder of the blunt-nosed vehicle shows some degradation in dynamic stability.
$\dot \theta $) together with the moment arm with reference to the centre of gravity. The results obtained for blunt-nose and truncated conical bodies show a noticeable drop in dynamic stability. Even when the flow is transformed from a tangential blowing at the shoulder of the blunt-nosed vehicle shows some degradation in dynamic stability.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Royal Aeronautical Society
References
- 1
- Cited by


