Sell now or later? A decision-making model for feeder cattle selling

Abstract

Given the relatively small industry scale of cow-calf operations in New York to other regions of the country, little is known about differences in determinant values for feeder cattle. Using auction prices and quality characteristics over 7 years, differences in market, lot, and quality parameters suggest opportunities for improved marketing performance. A delta profit model is constructed to inform timing of marketing decisions for producers. The results indicate a relatively high potential for producers to increase farm returns by delaying sales of lighter-weight feeder cattle from the fall to spring auction months, given sufficient rates of gain and reasonable overwintering costs.

Introduction

Considerable research has examined the market forces and cattle characteristics affecting cattle prices in the United States. Preferences necessarily vary by cattle production system (e.g., purebred breeders, cow-calf producers, cattle feeders) reflecting differential benefits to different segments of producers (Sy et al. 1997). Cattle feeders face high levels of variability in economic returns due, in part, to the variability in feed costs and fed cattle sales prices. In addition to spatial, temporal, grade, and varietal distinctions inherent in most agricultural commodities, buyers differentially value animals on the basis of weight, age, sex, and other characteristics as they relate to feedlot performance (Buccola 1980, Anderson and Trapp 2000). Assuming a fixed supply at a given market, demand for a feeder is based on how its characteristics influence aggregate beef production efficiencies and quality attributes demanded by consumers (Faminow and Gum 1986).

Feeder cattle are heterogeneous with prices that vary in economically important ways across animal and lot characteristics. Evolving market structures, consumer preferences, and production systems influence the relative values of various market and cattle characteristics on feeder cattle prices and, thus, require renewing attention. Buccola (1980) and Brorsen et al. (2001) provide enduring conceptual frameworks for the existence of price differentials by weight, sex, and important supply and demand factors. Empirically, hedonic pricing models are commonly used to assess these and other characteristics influencing feeder cattle prices (e.g., Faminow and Gum 1986; Schroeder et al. 1988; Lambert et al. 1989; Bailey, Peterson, and Brosen 1991; Coatney, Menkhaus, and Schmitz 1996; Dhuyvetter and Schroeder 2000; Blank et al. 2006; Barham and Troxel 2007; Troxel and Barham 2007; Blank, Forero, and Nader 2009; Leupp et al 2009; Schulz et al. 2010; Schulz, Boetel, and Dhuyvetter 2018).

Important cattle characteristics (beyond sex and weight) vary across study but generally include attention to lot size, breed, frame size, muscling, presence of horns, thriftiness, and utilization of preconditioning programs that prepare calves coming off pasture for a feedlot environment. ¹ Additional characteristics have emerged over time in alignment with evolving supplier demands, traceability concerns, and other consumer preferences, for example, third-party certifications (Bulut and Lawrence 2007) or specific vaccinations, implants for origin tracing, and disease testing (Zimmerman et al. 2012). Factors such as buyer competition and seller reputation have also been considered (e.g., Schulz, Dhuyvetter, and Doran 2015).

Similarly motivated hedonic models have been used in feeder cattle markets to examine local basis behavior (Mallory et al. 2016) and optimal hedge ratios (Elam and Davis 1990; Bina, Schroeder, and Tonsor 2021). Matching methods (e.g., nearest neighbor, propensity score matching) have received less attention but with a similar goal of estimating premiums of alternative “value-added” management practices (Williams et al. 2014a, 2014b). Hedonic pricing models in beef production systems extend beyond feeder cattle markets. For example, Jones et al. (2008) evaluate Angus bull prices using expected progeny carcass characteristics, and Smith et al. (2021) consider bred heifer and bred beef cow prices with emphases on cow characteristics important to successful calf production and expected finished cattle carcass characteristics.

Relative to dairy, fruits, and vegetable production in New York State (NYS), beef farming (cow-calf operations) generates considerably less in agricultural output; however, relatively large cattle feeders exist in NYS and nearby Northeast and Mid-Atlantic states due, in part, to their proximity to large consumer markets and demand for meat products. Feeder cattle sales represent the primary driver of farm profitability for cow-calf operations in NYS; however, little attention in the literature exists to the primary factors beyond those focused on the main cattle producing areas of the United States. This focus is understandable given enduring beef cow inventories over time and the industry’s importance to overall agricultural economic activity in those states. Of the top 10 beef production states, Texas ranks first in beef cow inventories (4,572,742 head) and Montana ranks first in average farm size (145 cows per farm) (USDA 2019). By comparison, NYS ranks 38^th in inventories (109,914 head) and 39^th in average farm size (15 cows per farm) (USDA 2019). Some production and marketing practices are likely indifferent to location and farm size, while others may vary based on agronomic, weather, and local market conditions (e.g., forage utilization, breed selection, and professional support services). To the degree that preferences for cattle and lot characteristics by feedlot buyers and regional market structures vary, more refined evidence-based recommendations for NYS producers can provide opportunities for improved returns.

While much of the hedonic and related literature identifies premiums associated with various management and marketing factors to improve feeder cattle prices, a more limited literature takes the next step to compare the levels of those premiums to their associated farm costs. Doing so requires additional farm-level data, assumptions, and/or estimation of implementation costs. For example, Anderson and Trapp (2000) conduct a breakeven price analysis for cattle feeders in response to corn price changes by simulating prices based on weight and incorporating ration costs, while Wang et al. (2001) consider the costs and returns of alternative marketing strategies (e.g., cash, futures, and options). Most common applications relate to the costs and returns of alternative quality and health management programs implementable by producers (e.g., Avent, Ward, and Lalman 2004, Williams et al. 2014b; Schulz, Dhuyvetter, and Doran 2015; Lalman and Mourer 2017).

The timing that producers bring their feeders to market can affect net farm returns and seasonal variation in feeder cattle prices is well known nationwide (i.e., lower in the fall than in the spring, all else constant). White et al. (2007) identify factor price disparity due to price risk over the feeding period suggesting that producers with known carcass potential may be better off retaining ownership through finishing or marketing their feeders in a way that better communicates their value. Schulz, Dhuyvetter, and Doran (2015) evaluate seasonality effects at Iowa auction markets for producers that, in part, might consider extending ownership of feeders from December to February. Tonsor and Mollohan (2017) consider producer timing of sales by examining price spread behavior between calves (500 pound) and yearlings (700 pound). In a NYS context, seasonality influences may provide an opportunity for producers to retain ownership of their feeders once they come off pasture in the fall, overwinter them, and then sell them the following spring.

The contributions of this research are twofold. First, we estimate a price-dependent, risk-responsive input demand model for feeder cattle based on auction prices at a NYS livestock exchange over the course of 7 years. The data encompass nearly 12,000 lots of feeder cattle over 54 auction dates. The pricing model considers a series of covariates, including market conditions, seasonality, lot size, and cattle quality characteristics (e.g., frame size, muscling, thriftiness, and the presence of horns). ² The pricing model provides for direct calculation of expected market prices for feeder cattle under differing weights, market conditions, and quality characteristics – something necessary as a decision aid when making production decisions and price forecasts.

Our second contribution applies forecasting from the pricing model to a seasonal delta profit model to inform cow-calf operators on the preferred timing of their feeders for sale, conditional on information available as animals come off pasture, and the expected feeding and management costs for overwintering. The delta profit model outputs the expected profit gain (or loss) for cow-calf operators to retain ownership of feeders in the fall and sell them the following spring relative to selling them in the near-term fall, explicitly accounting for price-weight slides (Dhuyvetter and Schroeder 2000). Transactions in the sample data indicating benefit to delayed sales are summarized to provide information to cow-calf operators on the conditions and cattle characteristics that present opportunities for improved farm returns.

We continue with a summary of the conceptual framework and the empirical pricing and seasonal profit models. The data are then described and empirical results presented. We close with some implications of our results and directions for future research.

Pricing model

Following Dhuyvetter and Schroeder (2000), a risk-averse cattle feeder (i.e., buyers of feeder cattle that feed to finishing) maximizes expected utility following equation (1):

(1) $$\max {\rm{E}}\left[ {U\left( \pi \right)} \right] = {\rm{E}}\left[ {U\left( {{p_L}{q_L} - {p_F}{q_F} - {p_C}{q_C} - Z} \right)} \right]$$

where U(π) represent the cattle feeders utility function, p _L and q _L are the finished (fed) cattle price and quantity, p _F and q _F are the feeder cattle price and quantity, p _C and q _C are the price and quantity of corn fed over the feeding period, and Z represents other costs. Maximizing (1) with respect to q _F and solving for p _F yields the buyer’s input demand function for feeder cattle. Since forthcoming corn and fed cattle prices are unknown at the time of feeder purchase, futures prices, $p_C^*$ and $p_L^*$ , are used as proxies for expected prices, with second moments σ _C and σ _L , respectively. Accordingly, the risk-responsive input demand is specified in price-dependent form as:

(2) $${p_F} = f\left( {p_L^*,{q_F},p_C^*,{\sigma _L},{\sigma _C},Z} \right)$$

Aggregating individual input demands for feeder cattle to an industry level and allowing for different production functions by weight and cattle characteristics gives the empirical input demand model for feeder cattle as:

(3) $$\matrix{ {P{F_{it}} = {\beta _0} + {\beta _{LCF}}LC{F_{it}} + {\beta _{LCFW}}LC{F_{it}}W{T_i} + \;{\beta _{CF}}C{F_{it}} + \;{\beta _{CFW}}C{F_{it}}W{T_i} + {\beta _{LCF}}{\sigma _{LC{F_t}}}} \cr { + {\beta _{CF}}{\sigma _{C{F_t}}} + {\beta _{MAR}}Margi{n_{t - 1}} + {\beta _{WT}}W{T_i} + {\beta _{WT2}}WT_i^2 + \;{\beta _L}LOTSIZ{E_i}} \cr \hskip15pt{ + {\beta _{L2}}LOTSIZE_i^2 + {\beta _S}Se{x_i} + {\beta _{SW}}Se{x_i}W{T_i} + {\beta _P}PreCo{n_i} + {\beta _{PW}}PreCo{n_i}W{T_i}} \cr \hskip-25pt{ + {\beta _M}Muscl{e_i} + {\beta _{MW}}Muscl{e_i}W{T_i} + {\beta _F}Fram{e_i} + {\beta _{FW}}Fram{e_i}W{T_i}} \cr \hskip-28pt{ + {\beta _T}Thrift{y_i} + {\beta _{TW}}Thrift{y_i}W{T_i} + {\beta _H}Horn{s_i} + {\beta _{HW}}Horn{s_i}W{T_i}} \cr \hskip-85pt{ + {\beta _C}COLO{R_C} + \;{\beta _M}MONT{H_M} + {\beta _Y}Yea{r_Y} + {\varepsilon _{it}},} \cr } $$

where PF _it is the feeder cattle price for lot i in time t, LCF _it is the live (finished) cattle futures contract price corresponding to the month feeder cattle in lot i are expected to be sold as finished, ³ CF _it is the average of corn futures contract prices relevant over the feeding period for feeder cattle in lot i, ⁴ and σ _LCF , and σ _CF are coefficients of variation of daily live cattle and corn futures prices for the previous 21 weeks. ⁵ Margin _t-1 is the computed 21-week cattle-feeding margin for fed cattle marketed the previous week. ⁶ In terms of lot characteristics, WT _i is the average weight of feeder cattle in lot i and LOTSIZE _i is the number of head in lot i, both included in level and quadratic forms to allow for nonlinear price response (Dhuyvetter and Schroeder 2000). LCF _it and CF _it are also interacted with WT _i and allow for differential hedge ratios across feeder weights (e.g., Bina, Schroeder, and Tonsor 2021). Dummy variables are included for animal sex (Sex = steers [omitted], heifers, bulls, or stags), preconditioning status (PreCon = yes or no [omitted]), muscling level (Muscle = light, medium [omitted], or heavy), frame size (Frame = large, medium [ommitted], or small), thriftiness (Thrifty = thrifty [omitted], unthrifty), the presence of horns (Horns = yes or no [omitted]), and hide color (Color = black [omitted], red, Hereford, brown, white, other, and mixed). ⁷ Finally, monthly dummy variables account for seasonality factors based on auction month (Month = March, April, May, September, October, November, or December [omitted]) and year dummy variables account for other year-fixed effects not otherwise accounted for (Year _i = 2011 [omitted] through 2017).

Weight (WT) interaction terms accommodate for differences in production functions and price slides for alternative feeder cattle characteristics. ⁸ The prior feeding margin (Margin) and monthly dummy variables (Month) are limited to their levels (no interaction effects). These model simplifications vary from Dhuyvetter and Schroeder (2000), although robustness checks (not shown) to their inclusion show little impact on marginal effects and price slide behavior for the key variables of interest. ⁹

Delta profit model

The empirical pricing model is utilized to forecast prices (PF) and per head sales (PF * WT) based on specific cattle characteristics and time of the year. In NYS, most feeder cattle are marketed in the fall (high supply) and, expectedly, receive lower prices for animals of similar weight class and quality than in the spring (low supply). Depending on expected prices in the fall relative to the following spring, it may be profit enhancing for cow-calf producers to retain ownership of their calves in the fall, overwinter them, and then sell them the following spring. ¹⁰ Understanding expected profit changes (ΔProfit) requires articulation of expected current (fall) and future (spring) sales prices (including price-weight slide behavior), overwinter feeding and management costs, and production performance (i.e., rate of gain), or:

(4) $$\Delta Profit = \left( {1 - d} \right){\rm{E}}[S{F_S}] - \left( {1 + r} \right)(E[S{F_F}] + {C_{FS}}),$$

where E[SF _F ] represents expected sales of selling in the nearby fall auction, E[SF _S ] is the same for selling the following spring, and C _FS represents feeding and management costs between the fall and spring sales dates. ¹¹ Given production risks during the feeding period, expected sales in the spring are discounted by an expected death rate of d = 0.75% (Cooper 2015). Similarly, opportunity costs of current (fall) sales and interests on feed and management costs incur a cost penalty of r = 2.5%. ¹² Defining each sales component, we have

(5) $$\Delta Profit = \left( {1 - d} \right)(P{F_S}(W{T_F} + gDAY)) - \left( {1 + r} \right)(P{F_F}W{T_F} + {C_{FS}}),$$

where PF _F and PF _S represent estimated feeder cattle prices in the current fall and following spring, respectively, using equation (3). WT _F is the current (fall) feeder cattle weight. The weight in the spring is sum of WT _F and the rate of gain per day (g) times the number of days on feed between sales dates (DAY). The rate of gain will vary depending on starting weight and farm feeding performance. For our purposes, we assume an average rate of gain of two pounds per day and a 6-month feeding period (180 days). Overwintering costs between fall and spring (CF _S ) are

(6) $${C_{FS}} = \left( {{P_C}{Q_C} + {P_H}{Q_H}} \right)DAY + FC,$$

where P _C and P _H are prices of corn and hay, respectively, over the feeding period, Q _C and Q _H are the respective quantities consumed per day, and FC are other fixed costs. We assume that feeders consume a daily quantity of corn and hay equivalent to 1.41% of their weight (Taylor 2007), accordingly the cost of gain is lower for lighter-weight animals. Given their strong historical correlation, P _H is assumed to have a positive proportional relationship with P _C , where P _C follows CF as defined above for the nearby corn futures contract and a P _H is taken from NASS (2019). ¹³

All feed inputs are assumed purchased at the beginning of the fall. Since feeder cattle weight is increasing during the feeding period, we use the average weight ( $\overline {WT} $ during the feeding period to calculate corn and hay feed input quantities. Fixed costs relate to facility and management costs (e.g., utilities, repairs, maintenance, and returns to management) during the feeding period and are assumed constant at $34 per head for a 6-month feeding period (Taylor 2007). Accordingly, C_FS is expressed as:

(7) $${C_{FS}} = 0.0141\left( {{P_C} + {P_H}} \right)\overline {WT} DAY + 34.$$

The delta profit model is a cash difference model, albeit including estimated costs to production risk, and opportunity and interest costs. It does not include the use of price risk management tools through purchasing/selling futures and/or options, or purchasing livestock revenue insurance. Doing so would necessarily augment the expected sales and costs portions of the model. We leave these adaptions to future research; however, identifying the extent of overwintering opportunities through our delta profit model does provide support to the adoption of price risk management practices during periods of retained ownership. Considerations for cash flow needs and income tax implications are also ignored and would require additional farm-level data to incorporate.

If ΔProfit > 0 , the expected net return in the spring (6 months later) is greater than the expected net return in the current fall, implying overwintering feeders is a preferred strategy based on currently available (fall) information. For each observation (sale) in our data, we compute the expected price at that point and the expected price 6 months later using equation (3). Variables that differ directly in the price forecasting of PF _F and PF _S include WT (level, quadratic, and interaction terms) and Month (via fall or spring sale). Existing cattle characteristics (e.g., preconditioning, muscling, thriftiness, frame size) are left constant. While our primary interest is on overwintering potential (from fall to spring), for completeness, we apply the delta profit model to all sales observations (i.e., in the fall and in the spring).

A strictly positive level of delta profit can be used based on producer preferences. To evaluate the sensitivity of our results, we use two delta profit thresholds: $0 and $25 per head, and consider mean and lower bound (95% confidence interval) point estimates of PF.

Data

Our analysis is based on transaction-level feeder cattle auction prices at the Finger Lakes Livestock Exchange in Canandaigua, NY, during the spring (March through May) and fall (September through December) seasons from October 2011 to April 2017. The data include transactions from 11,926 lots of cattle (3,565 in spring and 8,163 in fall) encompassing 35,703 head (10,588 in spring and 25,115 in fall) over 54 auction dates.

During the auction, the final price, number of animals, average weight, preconditioning status, sex, color, and the presence of horns are recorded for each lot. In addition, cattle are professionally evaluated by a trained enumerator for frame size, muscling, and thriftiness. Consistent with the literature, dairy breeds and dairy cross breeds are excluded from the estimation sample, as well as lots with average feeder weights less than 300 pounds or more than 900 pounds. The former bound is considered a minimum for successful feedlot transition performance (i.e., a significant price penalty occurs at auction for lower-weight animals), while the latter bound constrains lots to only those for which overwintering is feasible. The final data set includes 8,977 observations. ¹⁴

Table 1 provides descriptive statistics of our estimation sample. Feeder cattle prices averaged $139/cwt, but with considerable variation spanning $44 to $236. ¹⁵ Figure 1 depicts average auction prices by weight range compared to the nearby feeder cattle futures contract price. As expected, auction prices move similarly to the futures price (reflecting aggregate supply and demand conditions), but with noted volatility (reflecting differences in cattle characteristics to the feeder cattle futures contract) and to changes in local basis over time, particularly during 2014 and 2015. Similarly, corn and live cattle futures prices spanned relatively large ranges over the 7 years of data collection, with corn prices more than double in variation (CV) relative to live cattle futures (Table 1).

Table 1. Descriptive statistics of Finger Lakes Livestock Exchange beef feeder cattle auctions, 2011–2017, 300–900 pound average weight per head lots (N = 8,977)

Note: Auction data encompass from October 2011 to April 2017.

Figure 1. Average auction prices by weight range (lbs) and nearby futures contract prices for feeder cattle based on auction sate. Sources: Auction data from authors, CME (2021).

The average feeder weighed about 550 pounds (Table 1). While lots ranged from 1 to 61 head, there was a substantial number of smaller lots resulting in an average lot size of under 3. Nearly, 90% of lots contained five head or less. Most animals were without horns (dehorned or polled), thrifty, medium muscled, and carried a large frame size. More animals were preconditioned than not, but not by much (52%). Steers and heifers were evenly split encompassing over 80% of all animals at auction. Black animals (generally Angus) were by far the most common at auction (nearly 62%). As expected, considerably more lots were sold in the fall months (70%) relative to the spring (30%).

Empirical results – pricing model

Equation (3) is estimated using ordinary least squares (OLS) with clustered standard errors by auction date. Parameter estimates are reported in Table 2. An R-squared value of 0.736 suggests the model does well in explaining the variation in feeder cattle prices.

Table 2. Regression results for New York feeder cattle price determinants (N = 8,977)

Note: Pricing model estimated with ordinary least squares (OLS) for beef breed lots with average weight of 300 to 900 pounds per head. Model includes year-fixed effects (not shown) and clustered standard errors on auction dates. R ² = 0.736.

***, ** and * represent estimated parameters statistically different from zero at the 99%, 95%, and 90% significance levels, respectively.

Given the specification of our hedonic pricing model and the limited number of years in the data, separating the full sample into a restricted sample for price model estimation and another sample for the delta profit application is problematic. However, to consider out-of-sample model prediction accuracy broadly, we utilized a k-fold cross-validation approach where the full data set is randomly divided into k groups, or “folds,” of roughly equal size. Holding one fold out, the pricing model is fitted on the remaining k−1 folds and root mean squared error (RMSE) and R² values calculated on the observations in the holdout sample. The process is repeated k times using a different holdout sample, and the overall RMSE is the average of the k runs. The result was an average RMSE = 18.41 and R ² = 72.70. Comparing these to our full sample statistics (RMSE = 18.13, R ² = 73.50) shows only modest reductions in model performance in the restricted samples and providing confidence to the robustness of our results.

For ease of exposition and given the large number of quadratic and weight interaction terms, marginal effects (categorical variables) and elasticities (numerical variables) are also shown and discussed below (Table 3).

Table 3. Elasticities and marginal effects of New York feeder cattle price determinants

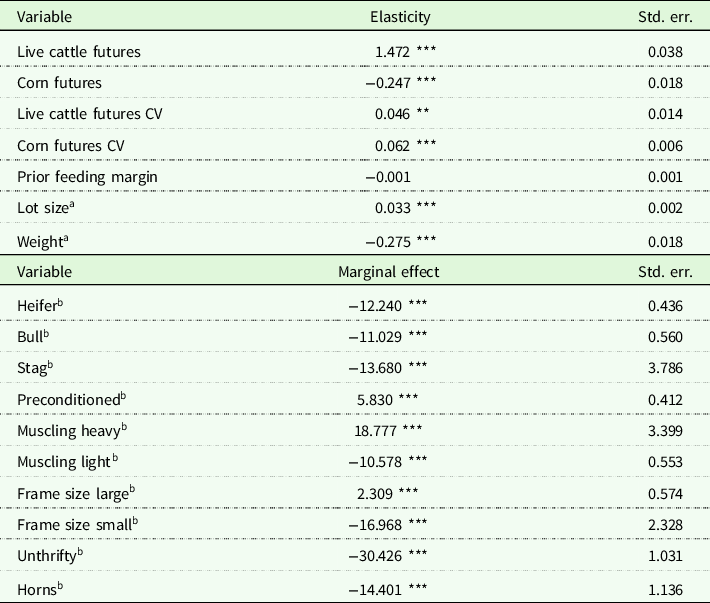
Note: Default categories for marginal effects are shown in Table 3. Elasticities and marginal effects computed at sample means.

^a Numerical variable included in level and quadratic form,

^b Categorical variable interacted with weight. Marginal effects for categorical variables not interacted with weight can be read directly from Table 3.

*** , **, and * represent estimated parameters statistically different from zero at the 99%, 95%, and 90% significance levels, respectively.

Market characteristics

As expected, live cattle futures (corn futures) is positively (negatively) associated with feeder cattle prices. The elasticities in Table 3 indicate that feeder cattle prices are considerably more responsive to changes in live cattle prices (1.472) than corn prices (−0.247). The association of volatility (CV) in corn and live cattle futures to feeder prices are positive, but relatively small (i.e., 0.062 and 0.046, respectively). Using auction data from Kansas for 1987 through 1996, Dhuyvetter and Schroeder (2000) find negative CV relationships; however, Schulz, Boetel, and Dhuyvetter (2018) using Wisconsin auction data from 2000 to 2017 find positive relationships and with an order of magnitude higher than ours. Changes in global markets over time and regional differences in feeding and finishing markets likely contribute to these differences. The prior feeding margin had a negative sign but was not statistically significant (−0.001) albeit similar in magnitude to Dhuyvetter and Schroeder (2000) (−0.004). ¹⁶

Lot characteristics

Consistent with the literature, we confirm the presence of nonlinear (quadratic) relationships between feeder cattle prices and lot size and animal weight. Price-weight slides are confirmed, whereby a 1% increase in feeder cattle weight is associated with a 0.275% decrease in price (Table 3).

Our results confirm a positive, albeit diminishing, impact of lot size on feeder cattle prices (Table 2). When computed at average weight, a 1% increase in lot size is associated with a 0.033% increase in feeder price. The results imply an optimal lot size of 27 head, far more than the average lot size exhibited in our data. The magnitude is consistent with Schulz, Boetel, and Dhuyvetter (2018) (44) and Dhuyvetter and Schroeder (2000) (219) for Wisconsin and Kansas, respectively, in the context of average beef farm and feedlot sizes, and associated trucking and related infrastructure utilized.

As expected, steers are preferred to either heifer or bulls, but with differing relationships with animal size (Table 2). For heifers, price discounts are reduced as animal weight increases. The opposite is true for bulls, where heavier bulls are increasingly penalized on price. The results are expected, heifers typically have lower daily gains, but as weight becomes higher there are fewer pounds (to finishing) impacted by this lower efficiency (Schulz, Boetel, and Dhuyvetter 2018). Lower meat quality and dressing percentages may also contribute to a price discount. Conversely, lighter-weight bulls are more conducive to castration after purchase and reductions in meat quality continue as a bull matures. Notably, at the average feeder weight (550 pounds), price discounts are comparable, even for stags (Table 3).

Quality characteristics

Accounting for changes in quality values as an animal grows is important for marketing decisions. Some management practices would appear simple and with minimal cost relative to the premium garnered. For example, a 300-pound horned feeder faces a substantial price discount of $16 per cwt (Table 2). Although decreasing with animal weight, the price discount remains over $14 per cwt at the average feeder weight (Table 3). Similarly, preconditioning a 500-pound feeder finds nearly a $6 premium. Finally, management practices promoting heavily muscled, medium to large frame sizes, and thrifty animals all return significant price premiums.

It is worth noting that these quality premiums exist irrespective of color/breed. Put differently, animal color price effects are controlled for separately in the model. While price discounts (relative to black) are modest for red, brown, and white feeders, more sizable discounts exist for Hereford (−$16) and Other (−$23) color/breeds (Table 2). Even preventing lots with mixed colors would negate a $9 per cwt price discount.

March and April sales dates, holding all else constant, garner price premiums in excess of $20 per cwt relative to December (Table 2). Relative to the October sales, those premiums are even larger. Less than seven full years of data may be insufficient for accurately estimating seasonality effects. Unfortunately, the length of our data is limited by the extent of our in-person collection of data at the sale barn over time. More data would certainly be better, although similarly motivated papers have used similar time series lengths with monthly dummy variables (e.g., 8 years: Schulz, Boetel, and Dhuyvetter 2018, 7 years: Schulz, Dhuyvetter, and Doran 2015, and 2 years: Bulut and Lawrence 2007). Coatney, Menkhaus, and Schmitz (1996) estimate quarterly seasonality variables with 1 year of auction data. Other than November (December default), the estimated coefficients on the month dummy variables are statistically significant, as is an F-test on their joint inclusion (F = 100.15, df = 6, p-value < 0.0001). Combined with nearly 9,000 sales transactions, we argue that 7 years of transaction-level data is sufficient.

Empirical results – delta profit model

The delta profit model, equation (5), includes three parts: expected sales of marketing feeders later (spring), expected sales of marketing feeders now (fall), and the feed and management costs incurred between the two points. Therefore, for a specific lot of cattle at a specific time, the delta profit model informs the timing of feeder sales based on currently available information. Based on the pricing model, weight and the related price-slide relationships are key factors. However, given quality factors are interacted with weight, the application is cattle-/lot-specific.

To provide additional context, we apply the delta profit model to all lots of feeders within the data sold during fall months. In this case, over one-half (51%) of the lots sold in the fall were expected at that time to return higher profits (ΔProfit > 0) if producers retained ownership for an additional 6 months and sold them the following spring (Table 4). When the per head threshold is increased to $25, nearly 45% of lots still qualify for overwintering. Using lower bound price estimates based on a 95% confidence interval reduces overwintering opportunities modestly to 44% and 39% for $0 and $25 per head profit thresholds, respectively.

Table 4. Percentage of observations exceeding ΔProfit thresholds, by season

Note: Includes all sales, feeder weight range 300–900 pounds. Results at the mean represent delta profit calculated at the mean (point) estimate from the pricing model; lower bound results are calculated using the lower bound price based on a 95% confidence interval.

Combined with the pricing model, a fixed rate of gain and feed costs proportional to animal size in the delta profit model increases profitable opportunities for overwintering lighter-weight cattle. So do the fixed death, opportunity, and interest cost rates. To illustrate, Table 5 breaks down the full sample fall sales results by 100-pound weight ranges. While cattle characteristics beyond weight may differ across weight ranges (and for that matter to the characteristic-weight interaction effects), the emphasis to lighter-weight cattle is clear.

Table 5. Percentage of fall observations exceeding ΔProfit thresholds, by weight

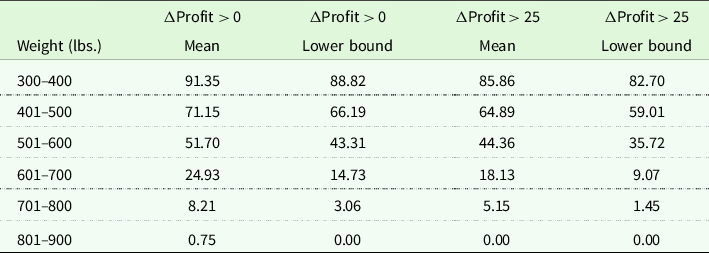
Note: Results at the mean represent delta profit calculated at the mean (point) estimate from the pricing model; lower bound results are calculated using the lower bound price based on a 95% confidence interval.

Finally, we compare descriptive statistics of the observations from the full, delta profit > 0, and delta profit > 25 samples to identify what characteristics are contributing most to overwintering beyond feeder weight. Recommended feeders for overwintering with delta profit > 0 (delta profit > 25) were 80 (90) pounds lighter, on average, than in the full fall sample. More specifically, we find that lots of cattle under lower expected feed (corn) costs (as expected) and higher market volatility (corn and live cattle futures CVs, think real options) show increased opportunity for overwintering, and particularly for lower-weight heifers with heavier muscled and smaller frame size characteristics. The level and interaction effects for market conditions and feeder characteristics in the pricing model drive these latter results.

Little opportunity exists to hold sales of feeders in the spring to the following fall. Only 4% or less (depending on threshold and price point estimate used) of spring sales were expected to generate higher net returns by holding them for an additional 6 months. Given the known seasonal variation in prices, this was expected, but other positive cattle weight interaction effects may offset price gains for spring months for feeders with particular characteristics. In general, there exist few situations where delaying spring sales to the fall make economic sense and likely only for the very lightest weight feeder calves where the cost of gain is lowest.

Conclusions

Given the relatively small industry scale of cow-calf operations in NYS in comparison to the primary cattle producing regions of the country, little is known about the differences, if any, in the primary determinants for feeder cattle prices in the state. We show that while some commonalities in the value of pricing determinants exist, for example, live cattle and corn futures prices, other conditions varied in their association with feeder prices (e.g., prior feeding margins, volatility in futures prices, and lot sizes), likely due, in part, to differences in local supply and demand conditions and industry scale effects. Furthermore, quality factors play an important role, with many within the control (and adjustment) of producers. The inclusion of 7 years of auction data for nearly 9,000 lots of cattle provides confidence in the robustness of our results.

Clear seasonality effects on feeder cattle prices may present opportunities for NYS producers to retain ownership of their feeder calves that are commonly marketed in the fall, overwinter them, and bring them to auction the following spring. Accordingly, a delta profit model was constructed using the feeder cattle pricing model as a forecasting tool, with production performance and expected feeding and management costs, to inform timing of marketing decisions for NYS producers. The results indicate a relatively high potential for producers to increase farm returns by delaying sales of lighter-weight feeder cattle from the fall to spring auction months, given sufficient rates of gain and reasonable overwintering costs, and particularly for lower-weight heifers with heavier muscled and smaller frame size characteristics.

As constructed, the delta profit model can also be used from a backgrounding program perspective. Specifically, the expected near-term sales in our delta profit model (E[SF _F ]) can be equivalently defined as a current feeder purchase cost and the 6-month delayed sales (E[SF _S ]) as expected feeder sales after backgrounding. The model can also be adapted to consider lot size effects on price, where feeders purchased are aggregated into larger, uniform lots for sale at auction later. This may be particularly appealing in NYS, where lot sizes are low (average lot size = 2.5 head) and singleton lots are not all that uncommon. Indeed, this occurs in practice, but for completeness would require consideration of additional costs in the profit model, including transportation and potentially higher health care costs of aggregating cattle from multiple farm sources.

Our delta profit model does not explicitly consider risk management tools in combination with delaying sales. Adoption of price risk management practices for the relatively small cow-calf operations in NYS is quite low, and with many operators supplementing their beef enterprises with off farm employment. Extending our baseline cash approach with price risk management scenarios for overwintering is a useful direction; however, doing so will require consideration of risk aversion coefficients of NYS farmers and the estimation of price risk distributions adaptable to our hedonic pricing model (see, e.g., Wang et al. 2001).

The average cow-calf operation in NYS has 15 cows suggesting many are part-time farming operations with additional off-farm income needed to support the farm household. Understanding differences in abilities or skill sets to address value-improving cattle quality characteristics in light of these findings is a needed direction to support industry growth and vitality. Given the potential for increasing net farm revenues through spring sales, an obvious direction for future research is to consider production costs associated with fall calving, a relatively rare practice in the state, in concert with the price analysis.

Finally, NYS is a large dairy state with more retail meat (in aggregate) produced through dairy farming than beef farming. Expanding on this analysis to consider dairy feeders similar to Schulz, Boetel, and Dhuyvetter (2018) is a needed extension to support NYS livestock industries in general, as well as to more comprehensively analyze beef–dairy–meat markets in the state in order to identify complementary and/or competing opportunities for agricultural industry growth.