Published online by Cambridge University Press: 05 October 2010
Theory that successfully explains the magnitude and range of estimates of protein retention (PR) efficiency from the cost of turnover of existing protein indicates that conventional curves for growth description are inappropriate for protein growth. A solution to this problem is found in the consideration that the rate-limiting steps for protein synthesis (PS) and breakdown are likely to be associated with the diffusion of metabolites in and between cells. The algebraic scaling of nuclear and cellular diffusion capacity with tissue or total body protein leads to a parameterization of the primal differential equation for PR (kg/day) based on two terms representing PS and breakdown, viz.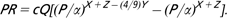 where c is an arbitrary constant, Q is the proportion of nuclei active in cell growth or division in a tissue or the whole body, α is the limit mass for protein (P, kg) in a tissue or the whole body, the power X+Z represents the rate-limiting steps in protein breakdown and Y is the power of the relationship between cell volume and the amount of tissue protein. For the whole body, the contribution of the different tissues should be weighted in proportion to their PS rates with, on average, Y = 1/2. The constant 4/9 arises from the scaling of the specific diffusion rate of DNA activator precursors from nuclear dimensions and from the relationship between nuclear and cell volume. Experimental evidence on protein breakdown rate as well as protein and body mass points of inflection indicates that the range of theoretically possible numerical values of the rate-limiting powers X+Z = (i+ 3)/9 for i = 1, 2, … ,12 seems adequate for the description of the range of observed whole body protein and body mass growth patterns for mammals. Q = 1 represents maximal protein retention, and for 0 < Q < 1, experimental evidence exists in support of a theoretical relationship between Q and food ingestion. The conclusion follows that some knowledge of the protein limit mass (α) and of the point of inflection (related to X + Z) is the main requirement for the application of the theory for description and prediction in animal nutrition and breeding.
where c is an arbitrary constant, Q is the proportion of nuclei active in cell growth or division in a tissue or the whole body, α is the limit mass for protein (P, kg) in a tissue or the whole body, the power X+Z represents the rate-limiting steps in protein breakdown and Y is the power of the relationship between cell volume and the amount of tissue protein. For the whole body, the contribution of the different tissues should be weighted in proportion to their PS rates with, on average, Y = 1/2. The constant 4/9 arises from the scaling of the specific diffusion rate of DNA activator precursors from nuclear dimensions and from the relationship between nuclear and cell volume. Experimental evidence on protein breakdown rate as well as protein and body mass points of inflection indicates that the range of theoretically possible numerical values of the rate-limiting powers X+Z = (i+ 3)/9 for i = 1, 2, … ,12 seems adequate for the description of the range of observed whole body protein and body mass growth patterns for mammals. Q = 1 represents maximal protein retention, and for 0 < Q < 1, experimental evidence exists in support of a theoretical relationship between Q and food ingestion. The conclusion follows that some knowledge of the protein limit mass (α) and of the point of inflection (related to X + Z) is the main requirement for the application of the theory for description and prediction in animal nutrition and breeding.