INTRODUCTION
In recent years, the development of seabed resources and the industrialization of cold regions have led to hydraulic structures, such as oil drilling platforms and artificial islands, being constructed in coastal and offshore areas exposed to sea ice pressure. These structures are being constructed directly on the ice sheet as well as founded on the seabed. Important in their design is estimation of the shear strength of sea ice. Shear strength is used in the calculation of the load-bearing capacity of the ice sheet as well as in estimating the horizontal pressure on structures built through the ice sheet. Testing methods to accurately estimate the shear strength of sea ice must be established, so that shear strength in various conditions can be determined.
Experiments were conducted in order to clarify the effects of the following:
-
i) the ratio of the diameter (d) to length (l) of the sea ice sample(d/l
-
ii) diameter of the sea ice sample (d)
-
iii) shear velocity

-
iv) shear stress rate (Ts)
-
v) sea ice temperature (T °C)
-
vi) vertical stress (σv) vii) growth direction of sea ice
TESTING METHOD AND APPARATUS
Experimental Apparatus
The experimental setup diagram is shown in Figure 1. The apparatus was designed to allow for the following:
-
i) use of variously sized sea ice samples
-
ii) variable vertical stress
-
iii) variable shear velocity
-
iv) variable shear stress rate
Testing Procedure
A horizontally movable shear box was used. Shear force was supplied by a hydraulic jack. The sea ice sample was placed in the circular hole in the shear box. Shear failure tests were conducted in this box. Static vertical loading was accomplished by placing weights on the sea ice sample via the steel cap. The shear velocity (thus, shear stress rate) was controlled by varying the hydraulic pressure applied to the jack.

Fig. 1. Diagram of the experimental setup.
Instrumentation
The sea ice sample was held immobile by the fixed lower half of the shear box. Shear velocity was measured using a standard displacement transducer attached to the movable upper half of the shear box. The shearing force was measured using a standard load cell connected to the movable upper half of the shear box. The vertical load was measured by weighing the added weights, steel cap and associated structure.
SEA ICE TEST SAMPLE
Cylindrical ice samples were used because they are easy to obtain using a core drill and are less likely to become damaged. Ideally, rectangular ice samples are desirable to obtain strain rates uniform over the entire shear plane; thus, directly relating the effects of strain rate to the direct shear strength of sea ice. However, in practice it is very difficult to obtain rectangular prismatic samples that properly fit the rectangular hole of the shear box.
The original ice block was sawed from the Okhotsk Sea ice field (coastal). Sample diameters were 10.0 cm and 15.0 cm, thicknesses were 3.0 cm, 5.0 cm, 10.0 cm and 15.0 cm. After a consideration of the grain size (8 - 12 mm in diameter) and ice sheet thickness (40 - 50 cm) of this sea ice, the standard sample’s dimensions were chosen: diameter 10.0 cm, thickness 15.0 cm.
Figure 2 shows the coring directions of the sea ice sample: vertical and horizontal in relation to the upper surface. The vertical core samples were tested perpendicular to the ice growth direction (GDJ-). The horizontal core samples were tested parallel to the ice growth direction (GD//).

Fig. 2. Diagram of the coring directions of the sea ice sample.

Fig. 3. The relation between Ts d/l

Fig. 4. The relation between Ts and d.
TEST RESULTS
Diameter to length ratio effects
Figure 3 shows the relation between the shear strength (TS) and the diameter (d) to length (I) ratio (d l l) of the sea ice sample. Although the test results exhibit scatter, it can be seen that the smaller the ratio (d/l) becomes, the larger the value of Ts becomes. Post experiment examinations of the fractured specimens showed two types of failure. In the case of d/l‹2, the failure was induced by shear only; with d/l›2, the failure was not caused by shear alone since the existence of a small gap between the ice sample and shear box introduced a bending moment.
Shear area effects
Figure 4 shows the effects of the shear area on shear strength; ie the larger the ice sample diameter the smaller the value of Ts became. An analogous relation exists in concrete. Future tests with larger sample diameters will have to be conducted to establish the relation between the s of a test sample and the Ts of the actual ice sheet.
Shear velocity and stress rale effects
Since ice is a visco-elastic solid, its shear strength varies with the strain rate ? and stress rate Ts.; thus, selection of the strain rate or stress rate is important when testing ice. When using cylindrical samples in direct shear tests, the strain rate over the plane of shear failure is not uniform; therefore, the authors determined the relation between Ts and shear velocity δδ.The three values, the strain rate i, stress rate TS and shear velocity 6s, are defined by the following equations:

where ∆l = strain, l = shear length, t = time to shear failure
strain rate: ![]()
Where τs = direct shear strength, t time to shear failure
Shear velocity: δs
Figure 3 shows the relation between the shear strength (τS) and the diameter (d) to length (j) ratio (d/j) of the sea ice sample. Although the test results exhibit scatter, it can be seen that the smaller the ratio
where Δ1 = strain, t = time to shear failure
Figure 5 shows the effects of shear velocity 6s on the shear strength. It can be seen that the shear strength Ts is relatively insensitive to changes in shear velocity in the range 0.01 to 1.0 mm/s; Ts broadly peaks about 0.1 mm/s.
Converting the sample’s circular cross section to an equivalent square cross section produces an equivalent shear length B, where B is derived as follows:
where d = diameter of the ice sample.

Fig. 5. Effects of shear velocity δ s on the shear strength τ s.

Fig. 6. Effects of shear stress rate T s on the shear strength
Using this shear length B in Equation 1 produces a strain rate ofof 0.001 se1at the maximum shear strength Ts. This value coincides with the rates found in compressive strength tests.
The relation between τs and shear stress rate Ts is shown in Figure 6. The shear strength Ts is relatively insensitive to changes in shear stress rate Ts in the range 0.1 x 106 to 10 x 106.N/m’.s.
Sea ice temperature effects
In general, the strength of ice depends on its temperature. The experimental relation between the shear strength and ice temperature is shown in Figure 7. Descriptively, the figure can be divided into two temperature regions: -2 C > T > -6 C and T < - 6 C. The shear strength clearly increases between -2°C and -6°C, but generally remains constant or decreases for T < -6°C. This phenomenon for T < -6°C, the remaining constant or decreasing of Ts, appears to be caused by the dilitancy of sea ice.
Vertical stress effects
The experimental relations between the shear strength Ts and vertical stress σv, as a function of ice temperature T, are shown in Figure 8(a) for 1981 and in Figure 8(b) for 1982, As can be seen,T s increases with decreasing ice temperature Ts increases linearly with increasing vertical stress σv for ice temperatures

Fig. 7. Relation of and τ s as a function of σv

Fig. 8a. Relation of τ s and σv as a function of T (1981).

Fig. 8b. Relation of τ s and σv as a function of T (1982).

Fig. 9. Relation between φ* and T.
higher than about -6°C; at lower ice temperatures (-9 C to -14°C in Figure 8(a) and -11 °C to -20°C in Figure 8(b) the relation between τs and σv is not linear. The results (at temperatures higher than about -6 C) coincide with Coulomb’s equation for direct shear strength; i.e., Ts and <r_ are linearly dependent.
Coulomb’s equation:
where C* friction, =apparent cohesion, Φ* = vertical stress.
angle of internal
Relation between φ* and T
The relation between the angle of internal friction Φ* and ice temperature T is shown in Figure 9. It can be seen that φ* increases with decreasing ice temperature when the shear force is applied perpendicular to the growth direction. With the shear force applied parallel to the growth direction, φ* tends to remain almost constant.

Fig. 10. Relation between C* and T.

Fig. 11. Application envelope of Coulomb’s equation.
Growth direction effects on C*
Figure 10 shows the results of the growth direction effect test on C*; ie, τs at σv = 0. Although the test results exhibit scatter, it can be seen that C* in shear planes perpendicular to the growth direction is generally greater than C* in planes parallel to the growth direction (at equivalent sample temperatures). With decreasing sample temperatures, the C* in planes perpendicular to the growth direction tends to increase more rapidly than in planes parallel to the growth direction.
Table 1. Results Of Five Years Of Sea Ice Experiments.

CONCLUSION
The application envelope of Coulomb’s equation
As determined from the results of five years of sea ice experiments summarized in Table I, the application envelope of Coulomb’s equation is shown in Figure 11. In region A, Coulomb’s equation is applicable for the determination of the shear strength of sea ice. The shear strength in region C is independent of vertical stress In C* region B, the relation between τs and σv is not linear because of the dilitancy of sea ice.
Ice temperature
The shear strength of sea ice increases, approaching a constant, with decreasing ice temperature (see TEST RESULTS - 4).
Shear velocity and stress rate
The shear strength is not greatly dependent on either the shear velocity or stress rate (see TEST RESULTS - 3).
Growth direction of sea ice
The shear strength in planes perpendicular to the growth direction is generally greater than in planes parallel to the growth direction (see TEST RESULTS -7).
Shear Area
The shear area experimental results (see TEST RESULTS - 2) indicate that the shear strength decreases with increasing shear area. Analogous relation exists in concrete.
Diameter to length ratio
The smaller the ratio becomes, the larger the value of τS becomes (see TEST RESULTS - 1).
ACKNOWLEDGEMENT
The authors express their appreciation to E. Suenaga for his assistance in the preparation of this paper.


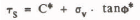
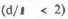 , the failure was induced by shear only. With d/
, the failure was induced by shear only. With d/












