Introduction
Numerical ice-sheet models calculate ice flow by coupling algorithms for internal-ice deformation, and basal-ice motion. Glen’s flow law for ice (Reference GlenGlen 1955) is in widespread use and different model formulations of internal ice deformation have been found to produce ice sheets which are in good agreement with one another (Reference Huybrechts and PayneHuybrechts and others, 1996). However there are various algorithms available to calculate basal ice-sheet motion (Table 1). Sensitivity tests have been carried out on the response of basal motion to variation in model parameters (Reference BentleyBentley, 1987). However, an intercomparison of ice-stream-sediment-deformation model techniques has yet to be investigated.
Table 1. Methods used to calculate basal ice-sheet motion
Reference PattynPattyn (1996) performed a flowline experiment comparing basal-motion models based on height-above-buoyancy and subglacial water flux in reconstructing the modern ice flux of the Shirase Glacier, Antarctica. However the flow-line nature of his experiment makes it difficult to generalize the results to a model of a complete ice sheet. Also, there was no long-term geological evidence available to compare the results from the models. In general, the highly multivariate nature of time-dependent ice-sheet models makes it difficult to select a simple comparison methodology to understand how sediment-deformation algorithms affect ice-sheet results. However, several authors have recently investigated the transport of sediment beneath ice sheets using numerical modelling Reference Jenson, Clark, MacAyeal, Ho and VelaJenson and others, 1995, Reference Jenson, MacAyeal, Clark, Ho and Vela1996; Reference Dowdeswell and SiegertDowdeswell and Siegert, 1999). Consequently it is increasingly important to investigate possible discrepancies between the available models for ice-sheet basal motion. This paper aims to highlight the effect of using two different methods for calculating ice-sheet basal motion. The models are applied to determine the sediment delivery to the margin of the Late Weichselian ice sheet in the Barents Sea. There are several features related to this former ice sheet which lend it to the experiment proposed here. First, a new ice-sheet reconstruction of the Late Weichselian Eurasian ice sheet has recently been conducted using the ice-sheet model, and associated environmental inputs, employed here (Howell and others, http://www.ggg.qub.ac.uk[rp05/1999]). Second, the presence of large glacigenic sedimentary fans on the margins of the Barents Sea provides a geological control on the model results. Late Weichselian sediment volumes have been measured on the Bear Island fan and the smaller Storfjorden fan (Reference LabergLaberg, 1996), along the western Barents Sea continental margin (Fig. 1). Third, the presence of the glacigenic sedimentary fans precisely locates the active ice streams which transported the sediment. Interfan margins are characterized by low sediment thicknesses, indicating that the ice sheet terminating in these regions was relatively inactive. Finally, there is currently a thick layer of soft, unconsolidated sediments throughout the Barents Sea. Thus, sediment transport during the relatively brief Late Weichselian glaciation did not strip the sediment layer from any part of the Barents Sea. Consequently, in modelling sediment deformation during this period, it can be assumed that the actual thickness of easily deformable sediments there exceeded the thickness of the shear zone within the subglacial sediments for the entire Late Weichselian glaciation. Therefore processes of sediment "creation and depletion" need not be considered, and the number of unknowns in the model is thereby reduced.

Fig. 1. Modern bathymetry of the Barents Sea (50 m contours). Transect AA′, used in experiments on sediment transfer to the western margin of the Barents Sea (Fig. 3) is shown. The current elevation of the transect AA′ is given in the inset. Bark shading is land above present sea level, light shading is the area up to 200 m below present sea level.
In summary, we have undertaken an intercomparison of two ice-stream-sediment models by applying the models to the well-documented glaciation of the Barents Sea with specific reference to a well-known glacigenic fan system. The results are valuable in themselves in the context of reconstructing the glacial and sedimentological history of the Barents Sea. The comparison of these two models also acts as an indicator that a more widespread comparison of all the basal-deformation models currently in use is needed.
The Numerical Model
The Late Weichselian Eurasian ice sheet was modelled using a topographic grid as a boundary condition, consisting of 310 (E) by 240 (N) 20 km × 20 km gridcells covering the United Kingdom, Scandinavia, northern Russia and the Barents and Kara Seas (Fig. 1). A time-dependent, vertically integrated, finite-difference, numerical ice-sheet model was used to determine ice-sheet flow, and an elastic-sheet lithosphere model used to calculate the isostatic depression caused by ice loading. In discrete experiments, the ice-sheet model was coupled to two subglacial sediment-deformation models.
Ice motion within the ice sheet was modelled by solving the continuity equation for ice flow (Reference MahaffyMahaffy, 1976);
where F(u, h) is the net flux of ice out of a cell (via internal deformation and basal motion of the ice sheet), and depends on ice-sheet thickness, h and velocity, u. The mass budget term, b, incorporates a number of processes including surface accumulation and ablation, iceberg calving and ice-shelf basal melting. Equation (1) is solved using an implicit finite-difference technique (Reference Huybrechts and PayneHuybrechts and others, 1996).
Internal ice-sheet deformation is modelled using a depth-averaged ice-velocity equation;
where
and τbx is the basal shear stress in the × direction, dependent on ice thickness, h, acceleration due to gravity (g = 9.81 m s"1), density of ice (ρi =910 kg m−3) and ice-sheet surface slope, a× (Reference PatersonPaterson, 1994). A is a flow-law parameter, here taken to be a constant (10–16 Pa−3 a−1) after (Reference Huybrechts and PayneHuybrechts and others, 1996), and the flow-law exponent used, n=3. Similar equations apply for motion in the y direction.
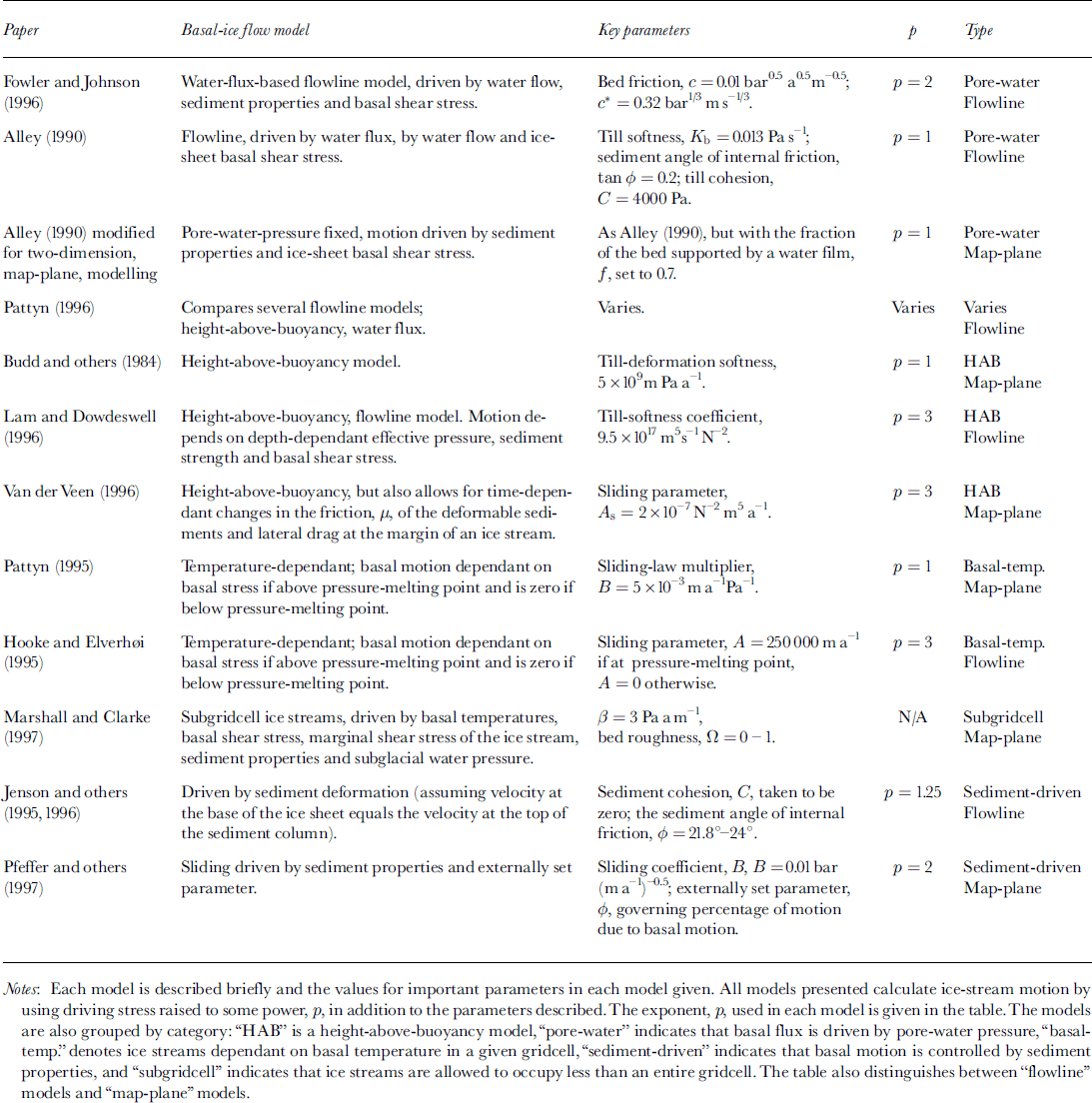
Modelling isostatic bedrock adjustment is after Reference Oerlemans and van der VeenOerlemans and Van der Veen (1984) and Reference Le Meur and HuybrechtsLe Meur and Huybrechts (1996). The Earth is modelled as a two-layer system, with an elastic lithosphere controlling the final isostatic depression and an underlying relaxed asthenosphere controlling the time taken to reach the equilibrium position. The lithosphere is modelled as an elastic sheet where an equilibrium depression caused by a discrete load at a point × = 0, is given by
where
and
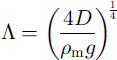
In Equations (3a)-(3c), × is the distance from the applied load, pm is the density of the mantle (3300 kg m−3), q× is the magnitude of the applied load, D is the flexural rigidity of the lithosphere, and X σ a Kelvin function of zero order. Reference FjeldskaarFjeldskaar (1994) determined that the flexural rigidity in Scandinavia was between 1 × 1024 and 1 × 1026 N m. Our study uses a flexural-rigidity value of 1 × 1025 N m. Equation (3a) is linear and, therefore, the total deflection of the lithosphere can be approximated as the sum of the deflections caused by discrete loads in each cell. The lithosphere is allowed to approach the equilibrium deflection computed in Equation (3a) by a exponential decay (Reference Le Meur and HuybrechtsLe Meur and Huybrechts, 1996):
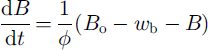
where B is the bedrock profile at time t, B0 is the original bedrock profile, wb is the bedrock depression from the original non-glaciated state, calculated from Equation (3a), and φ is a characteristic time constant governing the rate at which isostatic adjustment occurs. In each model year the lithosphere is adjusted by 1/0 times the distance to equilibrium (Equation (4)). In this paper φ is taken as 3000 years (Reference Le Meur and HuybrechtsLe Meur and Huybrechts, 1996). The value of 3000 years is compatible with that determined by Reference FjeldskaarFjeldskaar (1994) from Scandinavia, and with the raised-beach uplift data from the Barents Sea summarized by Reference LambeckLambeck (1995). This approach allows for modelling isostatic depression beneath the ice sheet, as well as more distal effects, including forebulges. The ice-sheet model described here is relatively insensitive to small changes in the environmental forcing parameters (Howell and others, ggg[rp05/1999]).
Environmental Conditions
Modelled ice-sheet growth is controlled by a number of environmental forcing functions. Spatially and temporally varying temperature and precipitation regimes have a significant effect on ice-sheet development. Global sea-level change is also influential in controlling the extent and growth of the ice sheet. These parameters are input as forcing functions into the ice-sheet model. However, in previous experiments, these inputs have been demonstrated to yield an ice sheet that is compatible with geological data relating to the extent of the last ice sheet (Howell and others, ggg[rp05/1999]).
Sea-level depression
The time-dependent change in sea level, adapted from Reference FairbanksFairbanks (1989) and Reference ShackletonShackleton (1987), is used to describe the variation in sea level during the last glacial cycle. The sea-level function has been corrected by the Reference Bard, Hamelin and FairbanksBard and others (1990) calibration so that it is in calendar years (Reference Siegert and DowdeswellSiegert and Dowdeswell, 1995). Our model therefore runs in calendar years. The sea-level curve is used to adjust bedrock heights through time, and to parameterize the transition between modern and glacial-maximum temperatures. Full-glacial conditions are assumed to coincide with maximum global sea-level depression, while modern sea level is correlated with modern climatic conditions.
Palaeoenvironmental conditions
The accumulation regime employed in this paper is identical to the one presented in Howell and others (ggg[rp05/1999]). There is a lack of data concerning the climatic regime of the Eurasian Arctic during the Late Weichselian. However, in previous experiments we employed an inverse-modelling procedure to produce an estimate of the accumulation regime throughout the Late Weichselian. Modern temperature and precipitation regimes have been established using the data presented by Reference VoseVose and others (1992). An initial estimate of the Last Glacial Maximum (LGM) temperature regime was obtained by adjusting modern values using the latitude-dependent variations proposed by Reference Manabe and BroccoliManabe and Broccoli (1985). The transition between modern and glacial-maximum conditions was parameterized using the sea-level curve of Fairbanks (1987) and Reference ShackletonShackleton (1987). The ice-sheet model was run using the initial estimate for climatic conditions, and the resulting ice-sheet limits were compared with those determined from geological observations. Changes were then made to the LGM temperature- and precipitation-regime end members to improve the correlation between the modelled and geologically determined ice-sheet limits. This process was iterated until a satisfactory match was obtained, as described in Howell and others (ggg[rp05/1999]).
Methodology
We use a time-dependent ice-sheet model, linked to a sediment-deformation model, to investigate the effect of different ice-stream models on glacigenic deposits for the Late Weichselian Barents Sea. The positioning of glacigenic sedimentary fans at the mouths of bathymetric troughs in the Eurasian High Arctic suggests that topographically controlled ice streams were the dominant factor in draining ice from the Barents Sea. Thus, any ice-stream model used in the context of the Barents Sea must locate ice-stream activity within major cross-shelf troughs. The existence of substantial glacigenic deposits also indicates that subglacial deformation was the dominant mechanism by which basal motion of the ice streams occurred and consequently basal sliding of the ice sheet is assumed to be negligible. These constraints make the glaciation of the Late Weichselian Barents Sea an ideal case study for conducting comparative tests on different ice-stream-sediment models.
The types of model available to simulate basal motion of an ice sheet are indicated in Table 1. The methods described may be broadly classified into height-above-buoyancy, subglacial-pore-water-pressure, basal-temperature and sediment-properties models. In addition, all of the models use the shear stress at the base of the ice sheet as a controlling factor on basal motion. As indicated in Table 1 some of these models are only suitable for flowline modelling (e.g. Reference AlleyAlley, 1990), and require modification to work in a map-plane reconstruction of an entire ice sheet. Furthermore, map-plane versions of models driven entirely by sediment properties (e.g. Reference Jenson, Clark, MacAyeal, Ho and VelaJenson and others, 1995, Reference Jenson, MacAyeal, Clark, Ho and Vela1996; Reference PfefferPfeffer and others, 1997) require ice-stream locations to be explicitly defined both spatially and temporally. The simple vertically integrated ice-sheet model employed here is isothermal in nature, that is, it cannot calculate basal temperature dynamically. As a consequence it is unsuitable for examining basal-motion models which rely on basal-temperature calculations (e.g. Reference PaynePayne, 1995; Reference Marshall and ClarkeMarshall and Clarke, 1997). However the ice-sheet model employed here is suitable for examining the two most widely used classes of models, where basal motion is dependant on height-above-buoyancy or pore-water pressure. In order to concentrate on the differences between the two classes of models, rather than specifics of each individual model, we have selected simple examples of each class of model for the experiments conducted here. We stress that this work should be seen as the beginning of a process of intercompanson of models, rather than an isolated exercise.
Two different experiments were designed, using independent methods for calculating basal motion beneath an ice stream: (1) using a height-above-buoyancy method (Reference Budd, Jenssen and SmithBudd and others, 1984); and (2) a modified version of Reference AlleyAlley’s (1989, Reference Alley1990) pore-water, pressure-driven, ice-stream model. In each case the basal motion was coupled with a depth-averaged sediment-deformation model. The ice-sheet model was run from the onset of glaciation until the initiation of glacial retreat, providing a calculation of the total sediment volume delivered to the edge of the continental shelf during the Late Weichselian. Sediment volumes deposited on trough mouth fans on the western margin of the Barents Sea during the Late Weichselian have been measured, indicating that approximately 4000 km3 of sediments were delivered to the Bear Island fan, and 700 km3 were deposited on the Storfjorden fan (Reference LabergLaberg, 1996). These estimates of sediment accumulation were compared with the sediment volume predicted by each model.
A full set of sensitivity tests was performed for each model to examine the effects of varying key parameters within the ice-stream and sediment models on sediment volume.
Height-above-buoyancy model
The first method for modelling basal motion of the ice sheet uses a height-above-buoyancy model to calculate effective pressure at the base of the ice sheet, and hence the basal velocity:
where
and Ne is the effective pressure, he is the height of the ice sheet above buoyancy and K is the till-deformation softness (5 × 109 m Pa a−1) (Reference Budd, Jenssen and SmithBudd and others, 1984). This basal-motion relationship is only valid for marine-based portions of the ice sheet, where buoyancy effects can operate, because height-above-buoyancy models produce basal velocities that are strongly dependent on water depth. Thus, ice streams are predicted within bathymetric submarine troughs.
Sediment transport is calculated by producing a depth-averaged sediment-deformation velocity, ![]() which is related to the velocity at the top of the sediment column by:
which is related to the velocity at the top of the sediment column by:
Where z is a depth averaging factor (0 ≤ z ≤ 1). We make a simplifying assumption that there is no significant exchange of sediment between the till layer and the basal-ice layer of the ice sheet. Consequently sediment flux can be modelled using a continuity equation, similar in form to the continuity equation for the ice sheet (Equation (1)).
It is assumed that the velocity at the top of the deforming-sediment layer is equal to the velocity at the base of the ice (i.e. all basal motion occurs through sediment deformation rather than ice-sheet sliding). At some depth, hb, within the sediment column, sediment-deformation rates will equal zero. The thickness of the layer of water-saturated sediments beneath Ice Stream B, Antarctica, has been found to be around 6 m (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986,Reference Blankenship, Bentley, Rooney and Alley1987). However modelling has suggested that, away from the margin of an ice sheet, the deforming thickness may be less than 6 m (Reference MurrayMurray, 1990). Reference Boulton and HindmarshBoulton and Hindmarsh (1987) suggested that most of the deformation within the sediment column occurs near the top of the sediment column. In order to account for this concentration of velocity at the top of the sediment column we use a deforming-sediment thickness, hb, of 5 m in the initial experiment combined with a depth-averaging factor, z, of 0.2. The combination of these values are in line with Reference Hooke and ElverhoiHooke and Elverhøi (1996) who used h b = 4 and z = 1/3, and Reference Dowdeswell and SiegertDowdeswell and Siegert (1999) who used hb = 2 and z = 0.5. The response of the sediment model to variations in hb and z are then subjected to extensive sensitivity testing.
As already noted the presence of pre-Late Weichselian soft sediments beneath subglacial till throughout the entire Barents Sea indicates a greater availability of deformable sediment than was actually mobilized during the Late Weichselian. We therefore assume that the depth of deforming sediment, hhb remained constant throughout the model run.
Pore-water-pressure model
The second method is based on that outlined by Reference AlleyAlley (1989, Reference Alley1990), where subglacial pore water is used to calculate the effective pressure, Ne, at the base of the ice sheet:
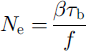
where β is a dimensionless roughness coefficient (0.45 from Reference AlleyAlley, 1990), and / is the fraction of the bed supported by a water film. For a till bed, as in the case of the Barents Sea, Reference AlleyAlley (1989) estimates fas:
where d is the thickness of the subglacial-water film in metres. Reference AlleyAlley (1989) notes that the water film beneath fast moving glaciers is likely to be on the order of 1–10 mm, giving / ≪ 0.7. Ice-sheet basal velocity is related to effective pressure by:

where Kb is a till-softness coefficient (taken as 0.013 Pa s"1, after Reference AlleyAlley, 1990), C is the till cohesion constant (4kPa), </> is the angle of internal friction (tan φ = 0.2, after Reference AlleyAlley, 1990), and hb is the deforming-till thickness. In the initial experiment we assume that ice-stream motion, within bathymetric troughs, occurs with / = 0.7. We also assume that no significant ice-sheet basal motion occurs outside the trough areas. This assumption is justified by noting that the glacially transported material at the margins of the Barents Sea is concentrated in trough-mouth fans. The effects of using different values for / and /3 are examined in sensitivity tests.
Sediment deformation is calculated using the same assumptions as for the height-above-buoyancy model. To keep the comparison between models as close as possible, the initial experiment uses a deformable sediment layer, hb, 5 m thick, with a depth-averaged velocity, z, equal to 0.2 of the ice-sheet basal velocity. The effects of variations in these parameters on sediment delivery to the continental margin are examined in sensitivity tests.
Results
Height-above-buoyancy model
The ice-sheet thickness and surface elevation produced for the Late Weichselian maximum in the Eurasian Arctic using the height-above-buoyancy model are shown in Figure 2a, b and c. The ice sheet produced in this reconstruction is the same as the one presented in Howell and others (ggg[rp05/1999]). Ice-sheet growth was initiated over Scandinavia and the High Arctic archipelagos, and is predicted to have expanded into the shallow marine Barents Sea by around 27 000 years ago. Glaciation of the Barents Sea was by means of ice flowing west from Novaya Zemlya, south from Svalbard and Franz Josef Land, and north and northeast from Scandinavia. The Barents Sea was fully covered with grounded ice by 25 000 years ago, and continued to thicken throughout the Late Weichselian. This increase in ice-sheet thickness led to the initiation of ice-stream activity in the StorfjordenTrough by 25 000 years ago, and the Bear Island Trough by 23 000 years ago. Ice-stream velocities rapidly increased to near their maximum by 21000 years ago, with the Bear Island ice stream flowing at up to 1000 ma−1, and >500 ma−1 in the StorfjordenTrough (Fig. 2c). By the glacial maximum at 18 000 years ago the entire Barents and Kara Seas were fully glaciated, with ice thicknesses of about 2000 m in the Barents Sea and 1400 m in the Kara Sea. Ice divides occurred on high areas over Svalbard (1400ma.s.L), Novaya Zemlya (1500 ma.s.l.) and Scandinavia. Ice flowed westwards from Novaya Zemlya into the Barents Sea and, subsequently, towards the continental margin. Ice flow out of the ice sheet was concentrated in the Bear Island Trough, resulting in a significant lowering of the surface elevation of the ice sheet in this region (Fig. 2a).
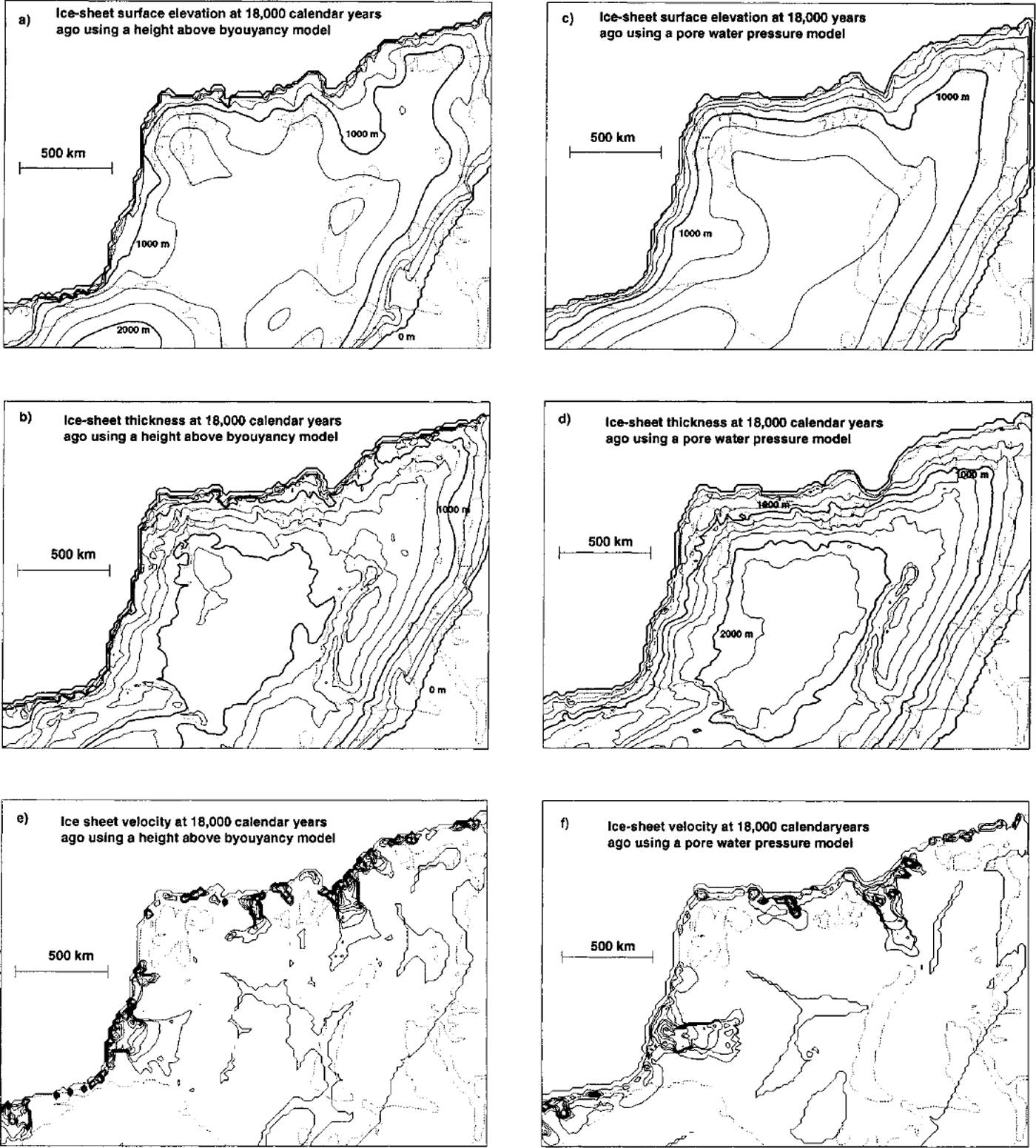
Fig. 2. The Eurasian High Arctic ice sheet modelled at the LGM. Using the height-above-buoyancy model: (a) Ice-sheet surface elevation (250 m contours); (b) ice-sheet thickness (250 m contours); (c) ice-sheet velocity (100 m a–1 contours). Using the pore-water-pressure model of Reference AlleyAlley (1990): (d) ice-sheet surface elevation (250 m contours); (e) ice-sheet thickness (250 m contours); (f) ice-sheet velocity (100 ma–1contours).
The sediment volume transported across a transect along the continental margin for the Late Weichselian is shown in Figure 3. The location of the transect is indicated in Figure 1. The mouth of the Bear Island Trough is the main region of sediment development, with 4200 km3 of sediments delivered to the continental margin during the Late Weichselian. We do not model sediment dispersal beyond the ice-sheet margin, rather it is assumed that the sediments delivered to the continental margin are then distributed over the Bear Island Trough mouth fan by a combination of gravity and current-driven processes. The Storfjorden fan is calculated to have received just over 900 km3 of sediments during the Late Weichselian.
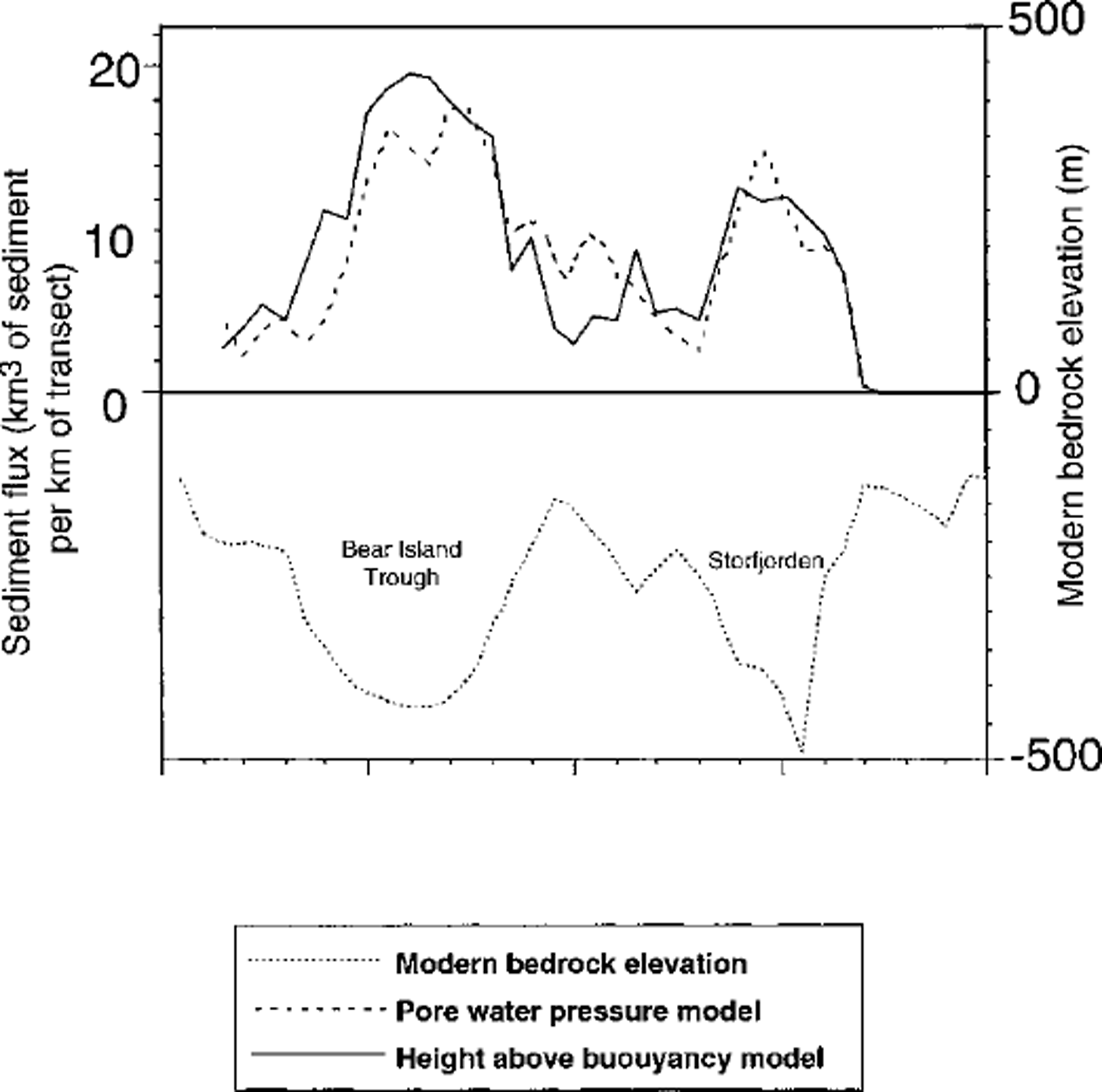
Fig. 3. Predicted sediment flux delivered across transect AA′ (Fig. 1) during the Late Weichselian ( inkm3/km) using a height-above-buoyancy model and the pore-waterfressure model of Reference AlleyAlley (1990). The modern bathymetry (m below sea level) is also shown for reference.
Sediment delivery under the height-above-buoyancy model is controlled by a number of parameters, most notably the depth-averaging function for till velocities, the thickness of the actively deforming sediment layer and the till-deformation softness, K. The sensitivity of the sediment volume to variation in these factors is shown in Figure 4. The model is pseudo-linearly sensitive to the thickness of the deforming sediment and the depth-averaging factor. This result is unsurprising, since basal motion of the ice sheet is not dependent on either factor (Equation (9a)), and consequently there is no feedback involved. The sediment volume is somewhat sensitive to the sediment-deformation softness-parameter, K, but small changes (±20%) to K do not result in the predicted sediment volumes on Bear Island lying outside realistic limits.
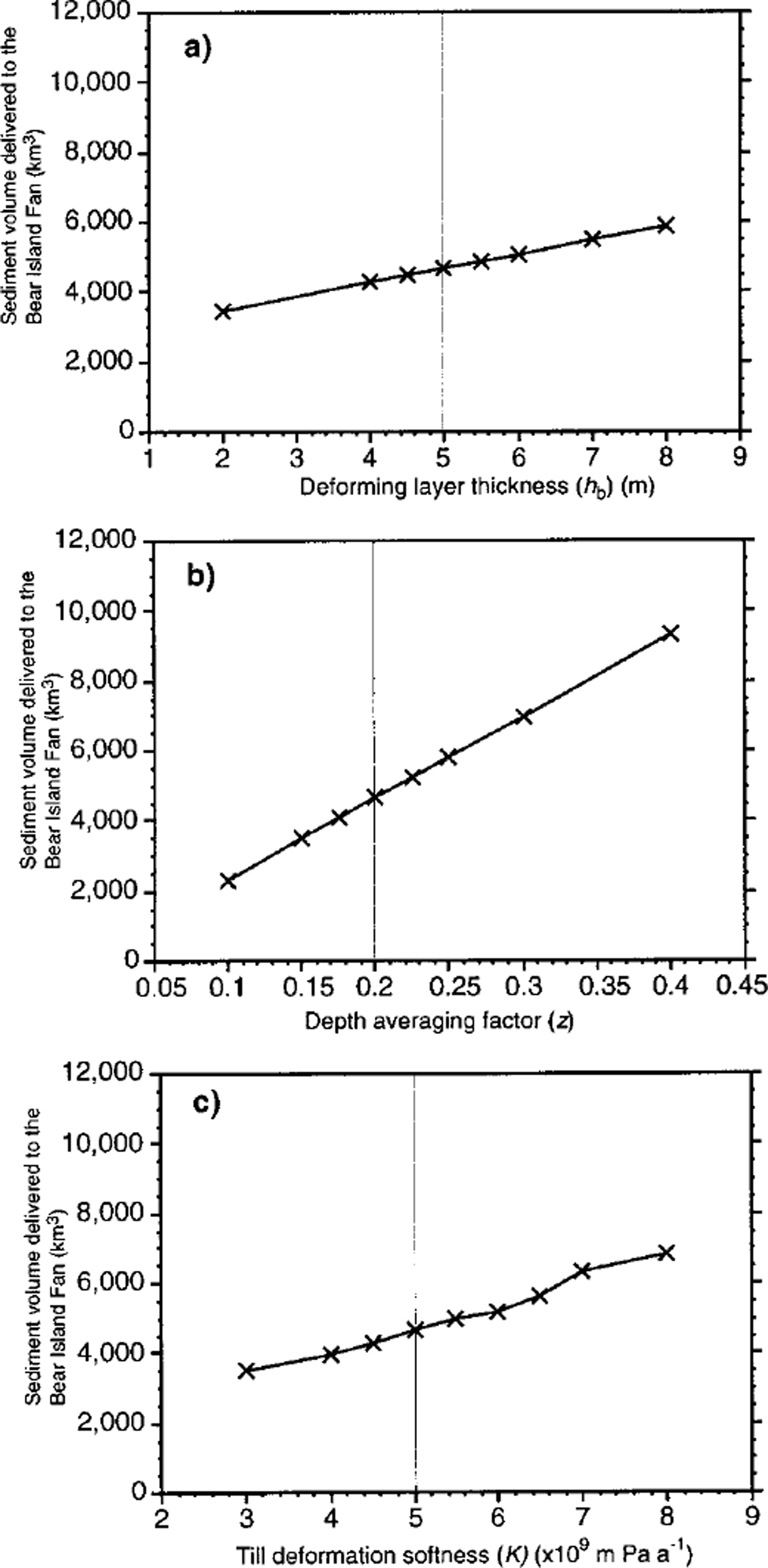
Fig. 4. Sensitivity of the volume of sediments (km3) to changes in model parameters for the height-above-buoyancy model calculated for the Bear Island fan. (a) Changes in sediment volume (km3) due to changes in the thickness of the deforming layer of sediments (m). (b) Changes in sediment volume (km3) due to changes in the depth-averaging factor used, (c) Changes in sediment volume (km3) due to changes in the till deformation softness ( mPaa1). The vertical line indicates the standard value used in these experiments.
Pore-water-pressure model
The ice-sheet thickness, surface elevations and velocity predicted for the Late Weichselian maximum in the Eurasian Arctic using the modified Reference AlleyAlley (1990) pore-water-pressure model are shown in Figure 2d, ε and f Ice-sheet growth during the Late Weichselian is similar to that predicted for the height-above-buoyancy model. By 18 000 years ago the entire Barents and Kara Seas are predicted to have been fully glaciated, with ice thicknesses of up to 2000 m in the Barents Sea and 1400 m in the Kara Sea. Note that the ice sheet produced using this basal-motion regime is broadly similar to that produced by the height-above-buoyancy model described above, with a similar depression of the surface caused by high ice fluxes from an ice stream in the Bear Island Trough. The ice sheet also exhibits spreading centres on Svalbard, Novaya Zemlya and Scandinavia, just as the height-above-buoyancy based reconstruction does, although there are small differences in the precise configuration of the two ice sheets as a result of the different basal-motion regime employed. Thus changes to the ice-stream model do not yield significantly different results.
Modelled sediment delivery to the western continental margin of the Barents Sea is summarized in Figure 3. Approximately 3800 km3 of sediment are delivered to the Bear Island fan, –10% less than the 4,200 km3 predicted under the height-above-buoyancy model. The pore-water-pressure model (Reference AlleyAlley, 1990) predicts around 1000 km3 of sediment at the margin of the Storfjorden Trough, slightly higher than for the height-above-buoyancy model. This is somewhat higher than the 700 km3 given by Reference LabergLaberg (1996), but is still in reasonably good agreement. Differences between the two models are most marked in the region between the Storfjorden and Bear Island fans, where ice velocities are lowest in both cases. The models are in reasonably close agreement in regions of high ice velocities.
The volume of sediment predicted to be delivered to the continental margin by the pore-water-pressure model is sensitive to the roughness coefficient, (3 (Fig. 5a), the till cohesion, C (Fig. 5b), the fraction of the bed supported by a water film, / (Fig. 5c), and the thickness of the actively deforming sediment layer (Fig. 5d). As with the height-above-buoyancy method, there is no feedback from the depth-averaging factor into the ice-sheet model, and consequently sediment delivered depends linearly on the depth-averaging factor used (Fig. 5). However the basal-ice velocity in the pore-water-pressure model is dependent on the thickness of the deforming layer and consequently there is a non-linear relationship between these two variables (Fig. 5). It can be seen that the model is relatively insensitive to changes (±50%) in the depth of the deforming layer. Deforming thicknesses, hb, of between 4.5 m and 6 m (combined with a depth-averaging parameter, z, of 0.2) yield sediment volumes broadly in line with the geological evidence. The sediment volume is somewhat sensitive to the till cohesion, C, where an increase of 50% results in 30% less sediment reaching the continental margin. A reduction of 50% in C produces 40% more sediment at the margin. Increases in the till cohesion beyond these ranges results in relatively little further change in sediment yield, however neglecting till cohesion entirely produces unrealistically high sediment volumes with some 6800 km3 of sediment being delivered to the Bear Island fan. The model is also sensitive to the fraction of the bed supported by a water film /, where an increase of 10% in / results in 20% more sediment yield, and a reduction of 10% in / lowers sediment yield by around 15%. Sediment yield also depends inversely on the roughness coefficient (3 (Fig. 5a). Small decreases ( φ10%) in (3 have relatively little effect on the sediment volumes, however decreasing β by more than 10% results in unrealistically easy deformation of the basal sediments, and consequent large increases in sediments transported to the continental margin (a sediment volume of 7200 km3 on the Bear Island fan for (3 = 0.2). Increasing (3 has much less of an effect on sediment yields.
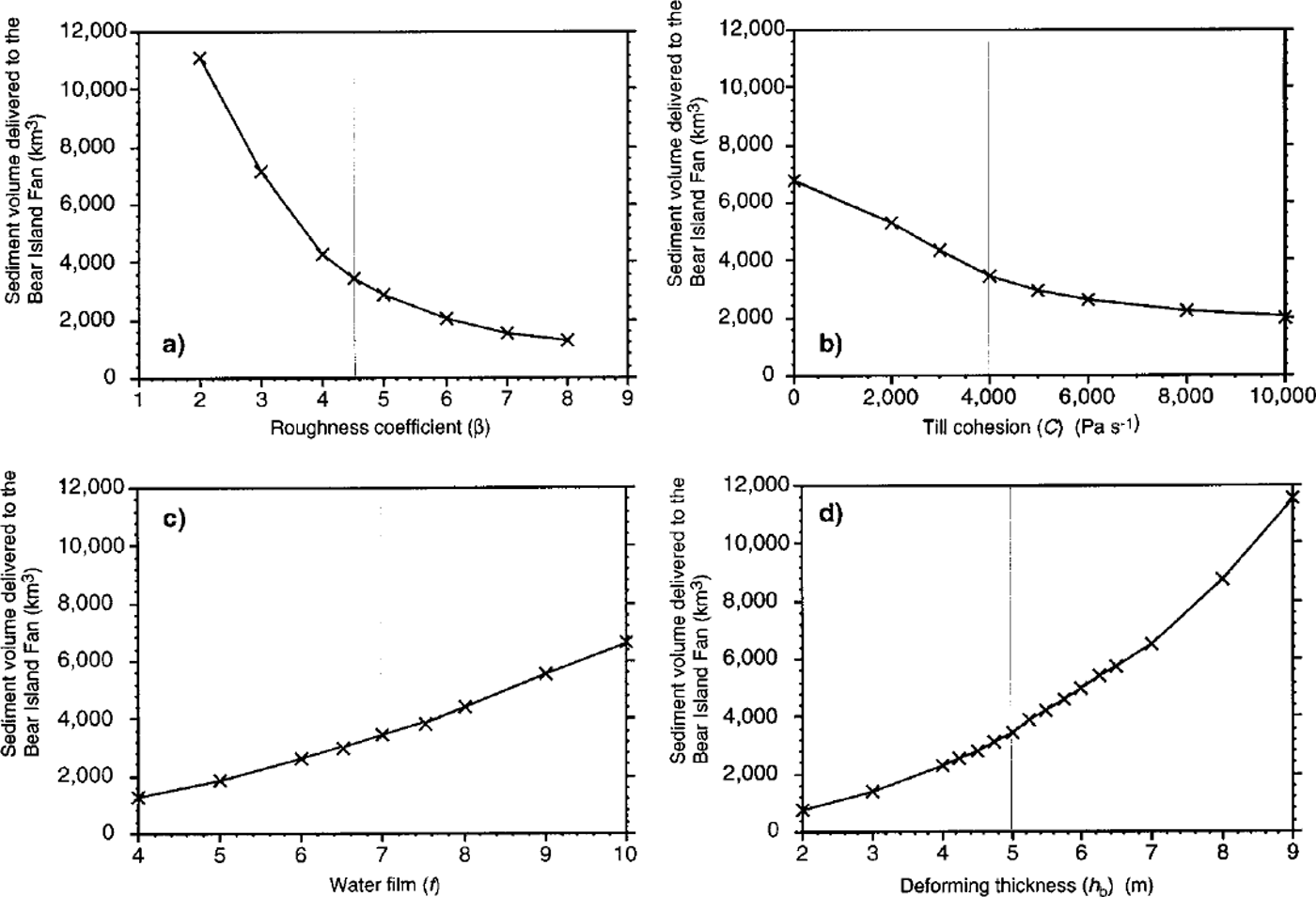
Fig. 5. Sensitivity of the volume of sediments (km3) to changes in model parameters for the Reference AlleyAlley (1990) sediment model predicted for the Bear Island fan. (a) Changes in sediment volume (km3) due to changes in the roughness coefficient, (b) Changes in sediment volume (km3) due to changes in the till-cohesion constant, (c) Changes in sediment volume (km3) due to changes in the fraction of the bed supported by a water film, ( d) Changes in sediment volume (km3) due to changes in the thickness of the deforming layer of sediments (m). The vertical line indicates the standard value used in these experiments.
Summary and Conclusions
The Late Weichselian Barents Sea ice sheet was underlain by soft deforming sediments, which were transported to the continental margins where they accumulated as large fans. A number of geophysical datasets are available from which measurements of the sediment volume over the Bear Island Trough (4000 km3) and StorfjordenTrough (700 km3) fans can be made. These measurements provide ideal geological data to test and compare models of ice-stream-sediment delivery.
We have used two different models for basal ice-sheet motion and sediment transport to reconstruct sediment delivery to the western continental margin of the Barents Sea during the Late Weichselian: (1) a height-above-buoyancy model and (2) a model based on the approach of Reference AlleyAlley (1990). These experiments allow an intercomparison of the respective models. Both are able to reproduce the observed volume of Late Weichselian sediment on the Bear Island fan accurately. The model results exhibit a degree of sensitivity to geotechnical properties of the deforming sediment, for which relatively little real-world control data exist. Both models depend on the till-deformation softness, while the Reference AlleyAlley (1990) model also incorporates the internal angle of friction. The velocity profile within the deforming sediments is also crucial to both models and is the subject of some uncertainty. However, neither model is highly sensitive to small changes in the major model parameters and, for both, changes to key parameters within a realistic range of values do not result in predictions incompatible with available geological data.
The two models presented here are dependent on different parameters, with the height-above-buoyancy model being dependent on the till softness, till depth, sediment-velocity-depth-averaging factor, basal shear stress of the driving ice sheet and topographic depth. The Reference AlleyAlley (1990) model also depends on basal shear stress, till thickness, sediment-velocity-depth-averaging factor and a till-softness coefficient. However, the angle of internal friction within the till, the sediment roughness, and the fraction of the ice-sheet bed supported by a water film also influence ice-sheet motion and sediment transport in the Reference AlleyAlley (1990) model, whereas they are not accounted for in the height-above-buoyancy model used here. Although both models incorporate a till-softness coefficient, this is formulated in different ways for the two models. The Reference AlleyAlley (1990) model defines till softness as a coefficient with units of Pas−1, while the height-above-buoyancy model defines till softness as a coefficient with units of m Pa a−1. This discrepancy arises from differences in the formulation of sediment velocity in the two models (Equations (5) and (9)). Furthermore, the way in which sediment volumes vary according to changes in key parameters differs between the models. In particular, the models exhibit different responses to changes in the thickness of the layer of actively deforming sediments, hb. The height-above-buoyancy model is linearly dependent on hb (Fig. 4a), while the Reference AlleyAlley (1990) model is non-linearly dependent on hb, and is more highly sensitive to increases in the thickness (Fig. 5d). For example, if the depth-averaging parameter, z, is held constant at 0.2, a change from hb = 2 m to hb = 4 m in the height-above-buoyancy model results in an increase in sediment volumes on the Bear Island fan of 810 km3, compared with 1518 km3 for the Reference AlleyAlley (1990) model. However a change from hb = 6 m to hb = 8 m in the height-above-buoyancy produces 818 km3 more sediment, compared with an increase of 3782 km3 for the Reference AlleyAlley (1990) model. Compared to the height-above-buoyancy the Reference AlleyAlley (1990) model is more sensitive to changes in the thickness of the deforming sediment layer, and is more sensitive at greater deforming layer thicknesses.
A number of other conclusions relating to the model intercomparison are:
-
(1) The geographical pattern of sedimentation is similar, though not identical, in the two models. Both models produce large volumes of sediment in the Bear Island and Storfjorderi Troughs, and relatively smaller amounts in the interfan region. For the Bear Island fan the height-above-buoyancy model produces 12% more sediment (4200 km3) than the Reference AlleyAlley (1990) model. The Alley model (1990) produces 10% more sediment than the height-above-buoyancy on the Storfjorden fan (1000 km3). Thus, the two models broadly agree on their predictions for sediment volume delivered to the major fan systems on the western margin of the Barents Sea.
-
(2) A higher degree of disagreement is found in regions where the sedimentation rate is lowest (i.e. small fans and interfan regions). For the region between the major Bear Island and Storfjorden fans, the Reference AlleyAlley (1990) model produces 28% more sediment than the height-above-buoyancy model, much greater than the 10% and 12% differences for the major fan systems.
-
(3) The location and ice velocities of major ice streams predicted by both models is broadly similar, with fast-flowing ice in the Bear Island Trough and the Storfjorden Trough, with slower-moving ice in between. The height-above-buoyancy model predicts ice velocities up to 1000 m a"1 in the Bear Island Trough, and 500 m a"1 in the Storfjorden Trough, with localized velocities of up to 200 m a"1 northwest of Bear Island. Much slower moving ice ( φ50 m a"1) characterized the rest of the continental margin. The Reference AlleyAlley (1990) model predicted ice flowing at around 1000 ma−1 in the Bear Island Trough, and 600 m a"1 in the StorfjordenTrough. Velocities elsewhere on the western margin were of the order of tens of metres per year, except for localized fluxes northwest of Bear Island and off northwest Svalbard.
In a small study of this kind it has obviously not been possible to compare all the available models for ice-sheet basal motion. The experiments performed here highlight the need for a large-scale review of the similarities and differences in reconstructed ice sheets produced by the different methodologies. This comparison should include more classes of models than in this preliminary study, more examples from each class, and may best be done as an analogue to the modelled internal ice-sheet dynamics testing exercises carried out as part of the European Ice Sheet Modelling Initiative (EISMINT) program (Reference Huybrechts and PayneHuybrechts and Payne, 1996).
Acknowledgements
D. H. acknowledges receipt of a PhD studentship from the University of Wales, Aberystwyth.








