1. Introduction
The propagation and diffusion of surface undulations on glaciers and ice caps have traditionally been a subject of considerable interest (e.g. Reference HutterHutter, 1983; Reference PatersonPaterson, 1994; Reference HookeHooke, 1998). The transient evolution of surface undulations is described by two time-scales: the diffusion time-scale (td) and the propagation time-scale (tρ). These time-scales are fundamental to the dynamics of large ice masses. A number of different theoretical estimates for td and tp have been put forward (e.g. Reference FinsterwalderFinsterwalder, 1907; Reference NyeNye, 1960; Reference Jόhannesson, Raymond and WaddingtonJόhannesson and others, 1989). On short to intermediate spatial scales ( ≤ 10/1, where h is the mean ice thickness), these time-scales are strongly affected by horizontal stress gradients (Reference JόhannessonJόhannesson, 1992; Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others, 1998). These theoretical concepts of the transient evolution of surface undulations have seldom been validated by a direct comparison with field measurements. This may be because surface undulations seen on glaciers are often the result of ongoing processes such as flow over bedrock bumps or differential ablation. For this reason it is often difficult to estimate accurately changes in geometry that are solely due to viscous relaxation of the ice.
An unusual event following a subglacial eruption of the volcano Gjalp (Fig. 1) in Vatnajökull, Iceland, in October 1996 unexpectedly opened the possibility of observing directly the transient response of an ice cap to sudden changes in geometry. The water created when large volumes of ice were melted during the eruption did not immediately drain away from the glacier, but accumulated in a subglacial lake, Grimsvotn, about 5 km south of the eruption site (Fig. 1). Only after the water level in Grimsvotn had reached a critical level, and about 3 km3 of water had accumulated in the lake, did water escape from the lake towards the glacier margin, resulting in a tremendous outburst flood (jokulhlaup) on 5 and 6 November 1996. The water drained out of Grimsvotn, forming an ice tunnel beneath the ice dam along the eastern flank of the nunatak Grimsfjall (Figs 1 and 2). Following the jokulhlaup, the roof of the ice tunnel collapsed, leaving behind a canyon about 100 m deep, 6 km long and 800 m wide.
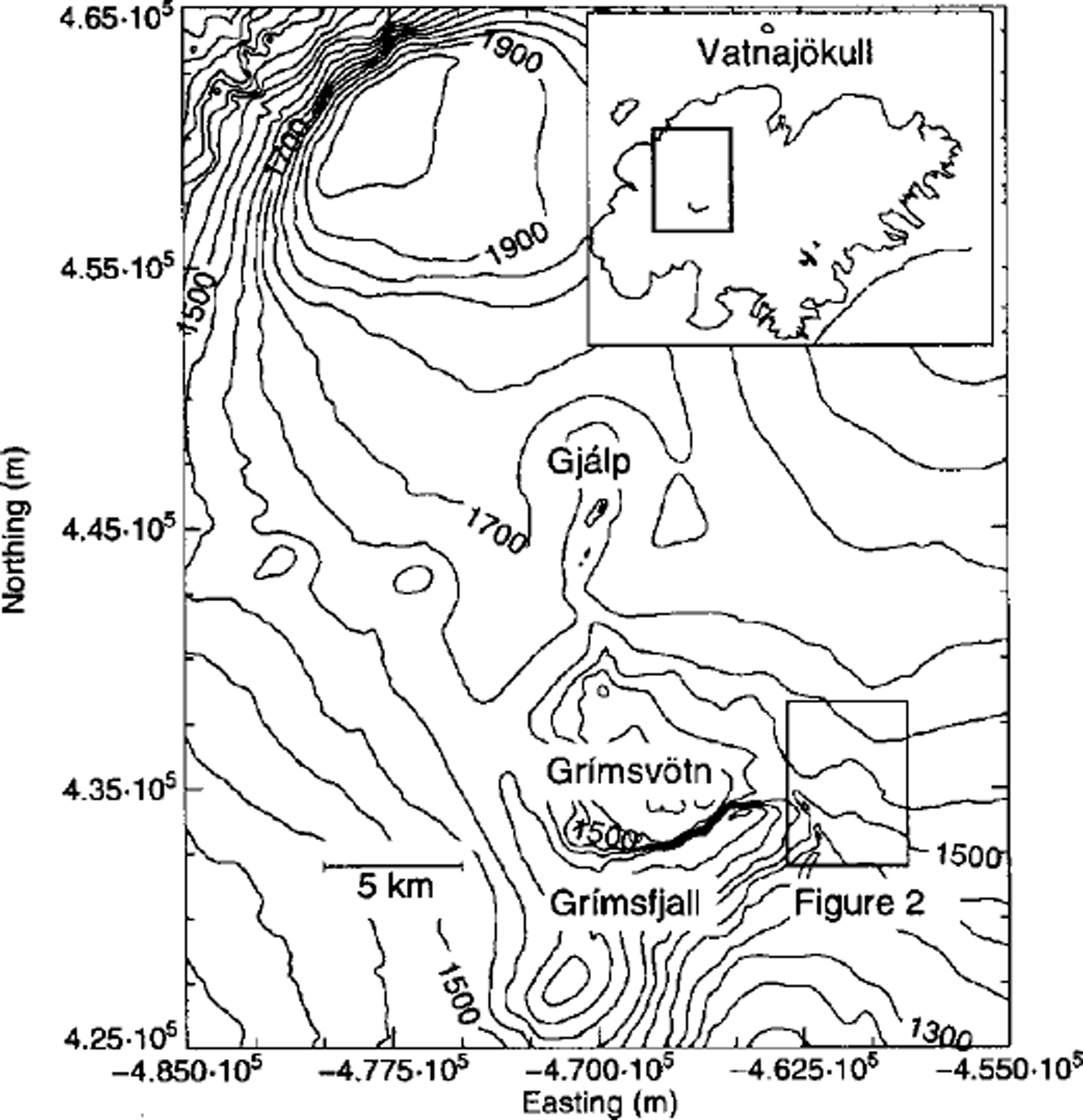
Fig. 1. Map of the northwestern part of Vatnajökull, showing the location of the 1996 eruption fissure, Gjálp, and the subglacial lake Grimsvötn. The contour labels give the ice-surface topography in meters above sea level. Inset shows the Vatnajökull icecap.
Jökulhlaups originate from Grimsvotn approximately every 5 years (Reference BjörnssonBjörnsson, 1988, Reference Björnsson1992; Reference Gudmundsson, Björnsson and PalssonGudmundsson and others, 1995). No visible surface depressions resulted from previous floods, although they and the November 1996 jokulhlaup all followed a similar subglacial route around Grimsfjall . This can be understood in light of the fact that the meltwater released in the November 1996 jokulhlaup had a temperature of about 6°C, whereas usually the water is at the melting point (Reference Gudmundsson, Sigmundsson and BjörnssonGudmundsson and others, 1997).
The purpose of this paper is threefold. First, we present measurements of changes in surface geometry and surface velocities along three transverse profiles across the canyon. Second, we discuss what kind of flow models are needed in order to estimate the closure rate of a surface depression of this type. We do so by calculating the transient surface evolution of idealized surface depressions having geometrical aspect ratios similar to the canyon’s, using two different analytical and two different numerical flow models. Essentially this discussion revolves around the question how strongly the closure rate is affected by the presence of horizontal stress gradients. Finally, we compare the results of a numerical simulation with field measurements.
2. Study Area
Vatnajökull is a temperate ice cap with an area of about 8300 km2 (Reference BjörnssonBjörnsson, 1980). Its western part covers an active volcanic zone. The Grimsvotn caldera (Fig. 1), approximately in the middle of the ice cap, is among the most active geothermal areas in Iceland, with frequent eruptions and associated jökulhlaups (Reference BjörnssonBjörnsson, 1988, Reference Björnsson1992; Reference Gudmundsson, Björnsson and PalssonGudmundsson and others, 1995). The subglacial lake Grimsvotn is sustained by geothermal activity within the Grimsvotn caldera. The fissure eruption in October 1996 of the volcano Gjalp took place about 5 km north of the Grimsvotn caldera (Reference Gudmundsson, Sigmundsson and BjörnssonGudmundsson and others, 1997).
The canyon created as a result of the 1996 jökulhlaup has an approximately north-south orientation (Fig. 2). To the west of it lies the mountain Grimsfjall. Grimsfjall is covered by ice a few tens of meters thick, except at the top which is ice-free. East of the canyon lies the glacier Skeiðarárjökull. There the ice is much thicker, around 300–400 m.
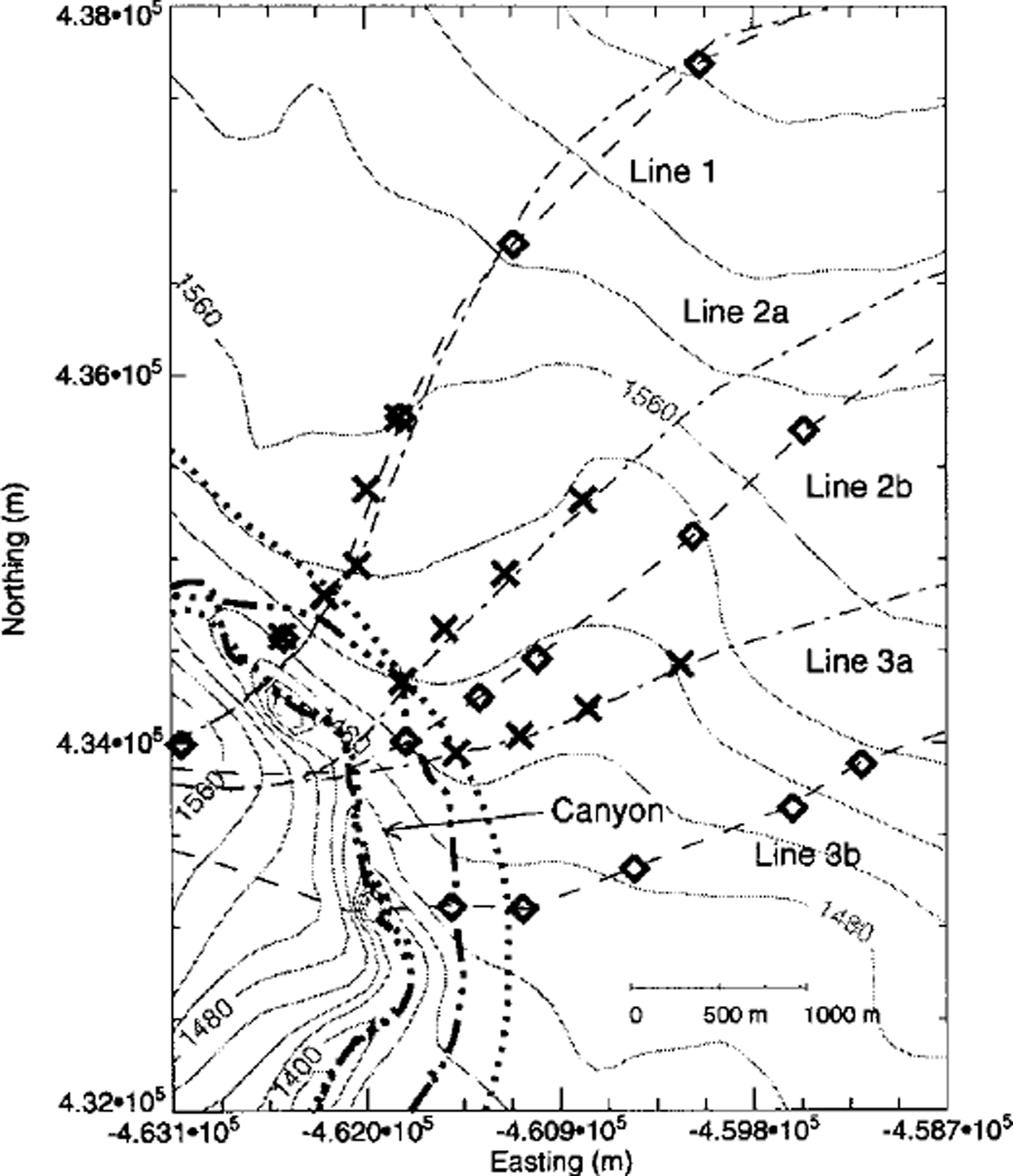
Fig. 2. Map of the study area showing the location of measurement stakes where summer surface velocities in 1997 and 1998 (crosses) and autumn velocities in 1998 (diamonds) were measured. The thin dashed and dash-dotted lines show various transverse profiles which are referred to in the text. The thicker lines mark the path of surface-elevation surveys.
3. Measurements
The surface and bed topography of northwestern Vatnajökull were surveyed prior to the eruption with radio-echo sounding methods (Reference BjörnssonBjörnsson, 1988; Reference Björnsson, Palsson and GudmundssonBjörnsson and others, 1992). The bed geometry of the area affected by the 19 96 jokulhlaup is therefore known. In June 1997 the surface elevation of the canyon and the surrounding area was surveyed using kinematic global positioning system (GPS) techniques. The measured profile is shown in Figure 2 as a heavy dash-dotted line. Three lines of stakes were drilled into the ice and surveyed in June and August 1997 with GPS equipment. Similar stake measurements were made in June and September 1998 (profiles 1, 2a and 3a in Fig. 2). In addition, velocity over a period of 29 days was measured on another set of three lines in August and September 1998 (profiles 1, 2b and 3b in Fig. 2). The surface elevation along the centre of the canyon and to the east of it was measured again in September 1998 (heavy dotted line in Fig. 2). In total there are thus two sets of elevation measurements within a time interval of 15 months, and several sets of velocity measurements along a total of six transverse profiles.
The results of the surface-elevation measurements were used together with existing topographic maps to create surface maps of the canyon and the surrounding area (database of the Science Institute, University of Iceland; personal communication from M.T. Gudmundsson, F Palsson and 5. Hognadottir, 1998). Unfortunately, no continuous transverse profiles of surface elevation could be measured in any of the field campaigns. Except for the measured position of the velocity stakes, the surface elevation along the transverse profiles is thus not known in detail. Transverse profiles of ice thickness along the measured velocity profiles were therefore generated by interpolating the surface and bedrock maps.
The measurements in 1997 and June 1998 were made with GPS equipment that has an accuracy of about 0.5 m in the horizontal direction and 1–2 m in the vertical direction. The August and September measurements in 1998 were made with instruments that have an accuracy of about 2 cm in the horizontal and about 5 cm in the vertical direction.
Figure 3 shows the results of the velocity measurements along transverse profiles 1–3. One of the objectives of the measurements was to determine if the presence of the canyon leaves a clear and unambiguous signature in the flow field along these transverse profiles. From inspection of Figure 3 it becomes clear that this is the case only for the 1997 measurements of profile 1, not for any of the other profiles. Evidently the velocity field, especially along profiles 2 and 3, is determined primarily by factors other than the presence of the canyon. Data for profiles 2 and 3 are thus not suitable for modelling purposes. The general flow direction along profiles 2 and 3 is towards the south, or the same as the overall slope direction. Since the surface slope increases somewhat in the downflow direction, going from profile 1 towards profile 3, and because the canyon is shallower along profiles 2 and 3 than along profile 1, it is not surprising that the effects of the canyon are observed most strongly along profile 1.
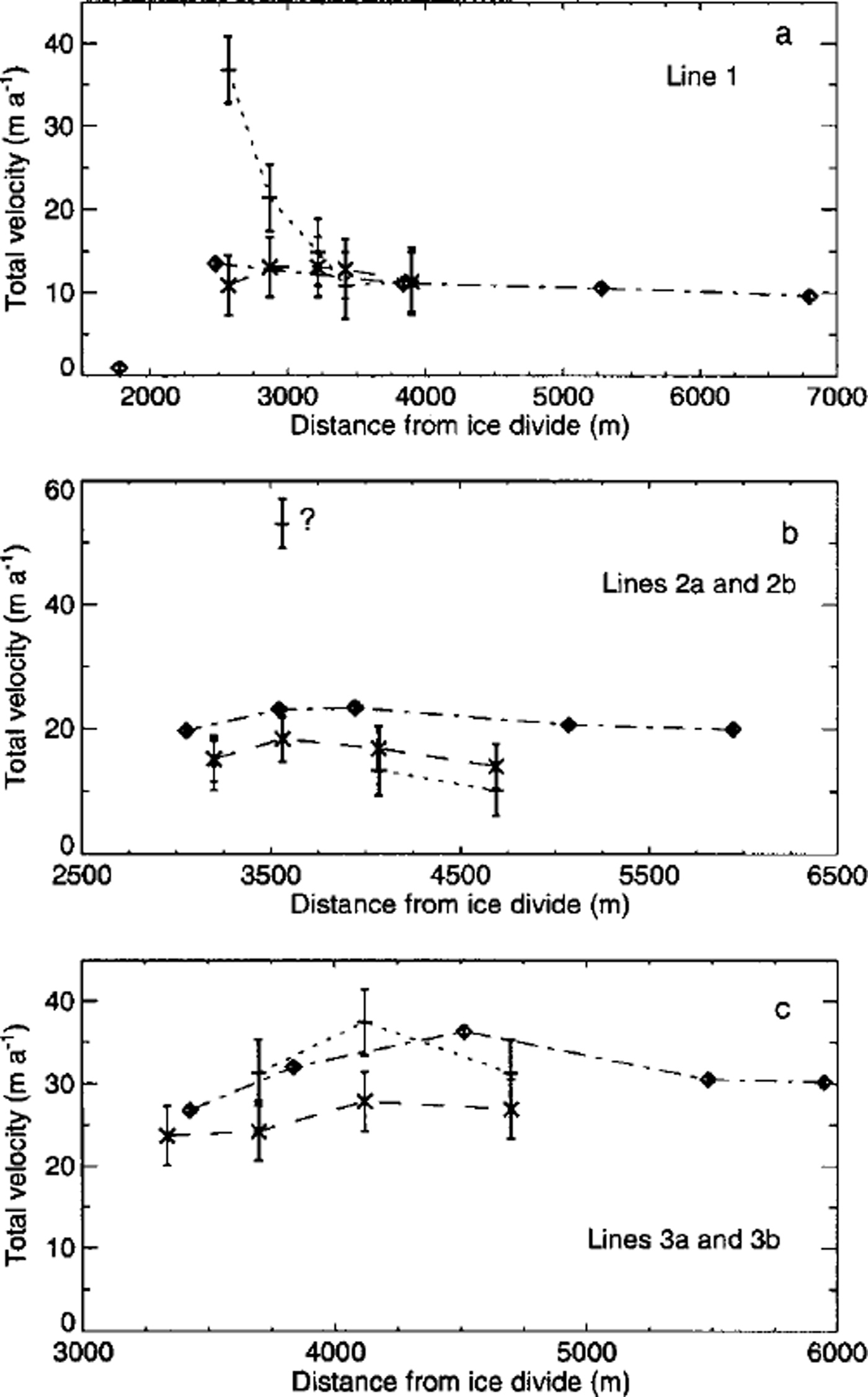
Fig. 3. Measured horizontal velocities along profiles 1,2a, 2b, 3a and 3b (Fig 2). Only the components of the horizontal velocity vector in the direction of the corresponding profiles are shown. Average velocities for June-August (summer) 1997 are shown as plus symbols, average velocities for June-August (summer) 1998 as crosses and average velocities for August-September (autumn) 1997 as diamonds.
It must be stressed that Figure 3 shows the components of the measured horizontal velocity vectors in the direction of the corresponding profiles. Directions of measured velocities are never exactly the same as the direction of the profiles. The difference between measured orientation of the velocity vector and the orientation of the profiles varies from stake to stake and with time. For profile 1 this difference is, for 13 of the 15 available velocity measurements, ≤ 20°. The two stakes where the difference was ≥ 20° were situated ≥ 5 km from the canyon.
There is no indication of a seasonal variation in measured surface velocities. It is conceivable that such changes are masked by ongoing changes in velocities due to the evolving geometry of the canyon. That would, however, be a rather unlikely and fortuitous cancellation of two effects.
4. Model Selection
We consider the closure of the canyon to be an example of a viscous relaxation process in an incompressible creeping medium. In principle, such a relaxation process can be modelled by solving the incompressibility equation
the linear and angular momentum equations
together with a constitutive law such as Glen’s flow law and a suitable set of boundary conditions. In the above equations, vi (for i = 1, 2, 3) are the components of the velocity vector, an are the components of the stress tensor and f are the components of the volume force.
In most (two-dimensional) modelling work on glaciers the starting-point is not the system of equations listed above, but the continuity equation
where h is the surface elevation, q is the ice flux and b is the mass-balance function. The flux q is then assumed to be a function of local slope and ice thickness, such that
![]() where n is a parameter in Glen’s flow law. In this approach all terms of the linear momentum equations involving horizontal stress gradients are ignored. Examples of such models are the shallow-ice approximation (SIA) (e.g. Reference HutterHutter, 1983) and the kinematic-wave equation (e.g. Reference NyeNye, 1960). These models are sometimes referred to as zeroth-order models.
where n is a parameter in Glen’s flow law. In this approach all terms of the linear momentum equations involving horizontal stress gradients are ignored. Examples of such models are the shallow-ice approximation (SIA) (e.g. Reference HutterHutter, 1983) and the kinematic-wave equation (e.g. Reference NyeNye, 1960). These models are sometimes referred to as zeroth-order models.
The kinematic-wave equation can be written as
where c 0 = ∂ x q(h(x), α(x), and D 0 = ∂ α q(h(x), α(x)), α is the surface slope, Ah is the surface perturbation with respect to some datum geometry and Ab is the accumulation function. If the datum geometry does not depend on x, this equation can be solved analytically. This leads to analytical expressions for the time-scales tp and td. We refer to the resulting zeroth-order theory of transient evolution of surface disturbances as the traditional kinematic-wave theory (TKWT).
The canyon was originally about 800 m wide, which is about twice the mean ice thickness of the surrounding region. This rather small width-to-thickness ratio suggests that only models which rigorously account for horizontal stress gradients will give accurate approximations to solutions of the full system of the field equations (Reference NyeNye, 1969; Reference Landon and RaymondLandon and Raymond, 1978; Reference Kamb and EchelmeyerKamb and Echelmeyer, 1986; Reference JόhannessonJόhannesson, 1992). The question thus arises how accurately the transient evolution of the canyon can be calculated with flow models such as the commonly used SIA. In order to answer this question, the transient evolution of a Gaussian-shaped surface depression, with geometrical aspect ratio similar to the canyon’s, was calculated using a number of different models for both a linear medium (n = 1) and a non-linear medium with n = 3.
Figure 4 shows the geometry of a Gaussian-shaped surface depression for t = 0.5 year as calculated using four different models for a linear medium. The predictions of the zeroth-order theories SIA and TKWT are almost identical, which is not surprising as the same set of assumptions underlies both theories. The only essential difference is that TKWT is a perturbation theory where the surface perturbations are assumed to be small compared to the mean ice thickness. For an initial depth at the centre of the depression of 100 m and a mean ice thickness of 400 m, the depth-to-thickness ratio is clearly not small. Reducing the depth of the depression by a factor of 10 results in an almost perfect agreement between the predictions of the SIA and of the TKWT.
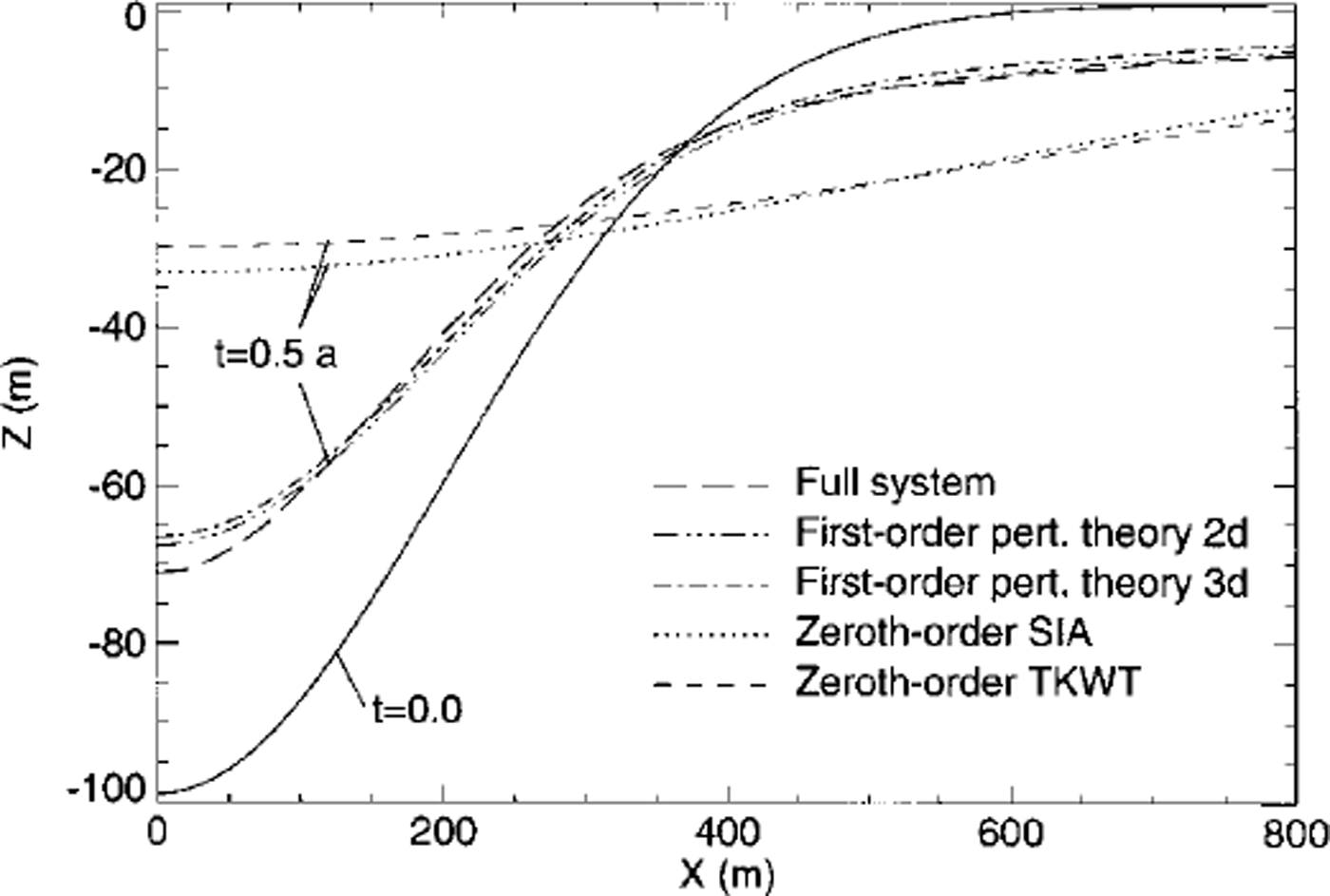
Fig. 4. Transient evolution of a Gaussian-shaped surface depression. The initial shape of the depression at t=0 is shown as a solid line. All other lines depict the shape at t=0.5year, as predicted by four different flow models. The two dash-dotted lines are based on an analytical first-order perturbation theory, for an infinity long depression (two-dimensional), and a depression having a length in y direction comparable to that of the canyon (three-dimensional). The long-dashed line follows from a numerical calculation with a transient finite-element model which solves all terms of the field equations. The dotted line is the prediction of the SIA, and the short-dashed line is based on TKWT. The flow parameters used in the calculations were n=1 and A = 1.0 × 10 –6 Pa– 1 a–1 The mean ice thickness was 400 m, the half-width (σx) was set equal to 200 m, the half-length (σy) was set equal to 3 km (relevant only for the dash-dotted curve (three-dimensional) ) and the initial depth of the surface depression was 100 m.
The dash-dotted lines in Figure 4 are calculated using a transient three-dimensional first-order perturbation theory developed by G. H. Gudmundsson (unpublished information). The relevant analytical solutions can be seen in Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others (1998) where the solution procedure is outlined. Reference JόhannessonJόhannesson (1992) worked out the transient solutions in two dimensions using different methods. The perturbation theory takes horizontal stress gradients into account.
The transient evolution of the surface depression is also calculated with a commercial finite-element model which solves the full system of the field equations in one horizontal dimension. The finite-element program was customized for ice flow by Reference GudmundssonGudmundsson (1994), and further developed by Reference LeysingerLeysinger (1998) for calculations of transient flow.
The shapes at t = 0.5 year predicted by the first-order perturbation theory (dash-dotted line) and the full-system finite-element calculation (long dashes) are almost identical, but differ strongly from the predictions of the SIA and the TKWT (Fig. 4). This demonstrates the importance of horizontal stress gradients for the transient evolution of surface depressions having geometrical aspect ratios similar to those of the canyon. Calculations using other Gaussian-shaped surface depressions having width-to-ice-thickness ratios of >20 and depth-to-ice-thickness ratios of ω0.05 resulted, on the other hand, in identical results for all four models. The exercise was repeated for n = 3 using the SIA and the full-system numerical model, with essentially identical results with regard to the importance of stress gradients at different spatial scales. It can thus be concluded that a model including stress gradients must be used for a realistic simulation of the transient evolution of the canyon.
5. Model Calculations
5.1. Numerical aspects
The numerical model used for simulating the transient evolution of the canyon is a two-dimensional finite-element model which solves Equations (1) and (2), and uses Glen’s flow law as a constitutive relation. The preceding discussion shows that commonly used approximations such as the SIA cannot be used. Basal sliding is ignored.
Quadrilateral strictly incompressible plain-strain elements are used in the model calculations. The size of the elements varies within the mesh, with widths in the range 80–90 m and heights in the range 3–60 m. The surface evolution is calculated by explicit forward integration in time of the kinematic boundary condition
(ignoring accumulation), using a two-step Lax-Wendroff scheme. The numerical model has been extensively tested by comparing it with analytical solutions based on perturbation analysis (Reference LeysingerLeysinger, 1998). The size of the time-steps must fulfil the Gourant stability condition (vΔt/Δx)2ω1, where v is ice speed, Δx is a typical elements size and At is the size of the time-step. For most of the calculations time-steps of 3 months were used.
5.2. Model tuning and verification
The use of Glen’s flow law introduces two parameters A and n. We treat the rate factor A as a freely tunable parameter which can be set to any value that will minimize differences between measurements and model calculations. The sensitivity of the model with respect to variations in n was also tested.
The model was run forward in time for a time period of 15 months, with the measured surface geometry along profile 1 in June 1997 as an initial upper boundary. Figure 5a shows the velocity along four selected vertical sections for the initial model geometry. Note the extrusion flow (increase in horizontal velocity with depth) in the east flank (to the left in the figure) of the canyon, which would not be predicted by the SIA.
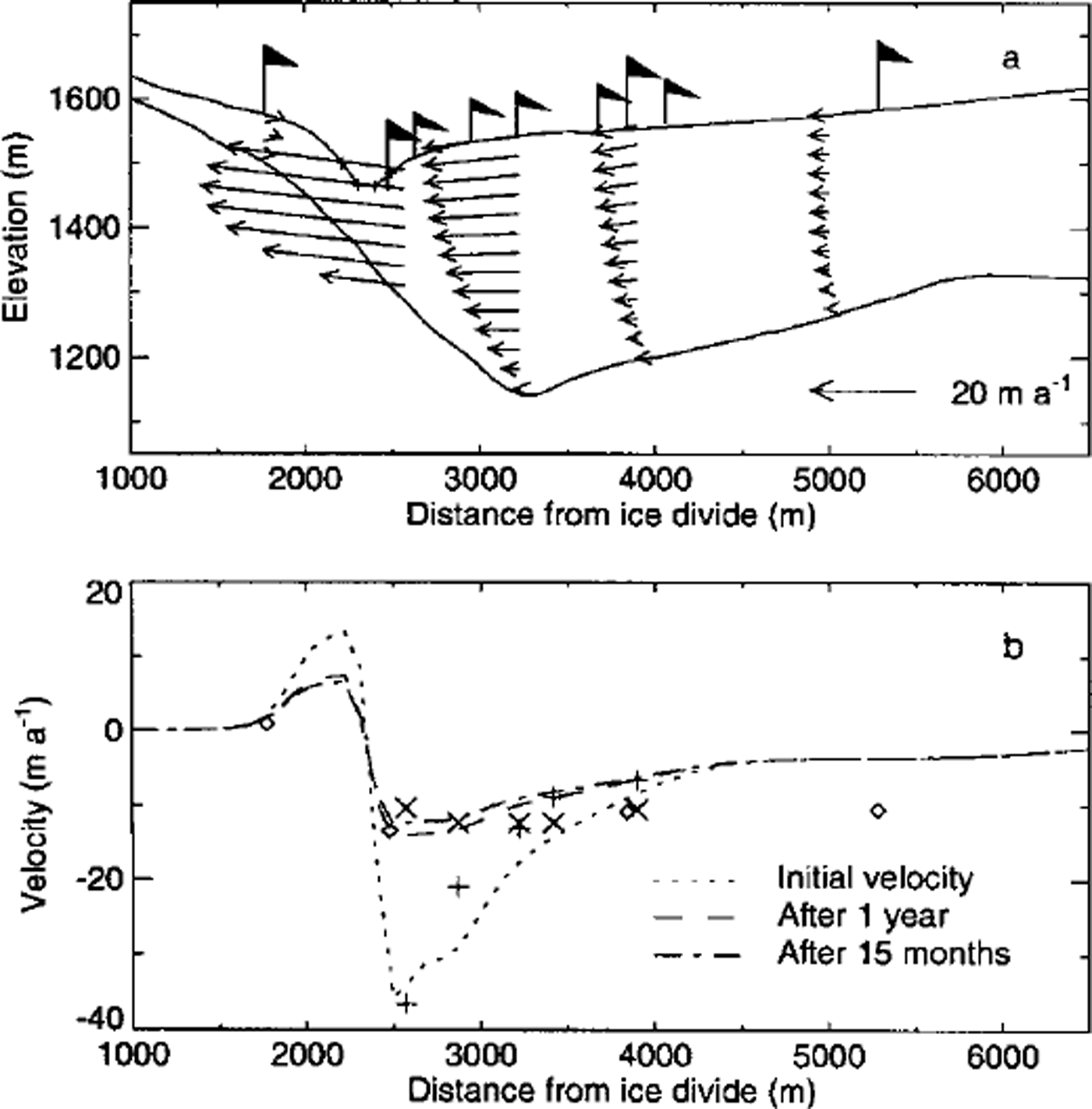
Fig. 5. (a) Calculated velocities along four vertical sections on profile 1 for the initial model geometry. The flags indicate the location of velocity measurements, (b) Calculated velocities along profile 1 for the initial model geometry (dotted lines), after 1 year (dashed line) and after 15months (dash-dotted line). Measured velocities are plotted for comparison. Plus symbols correspond to the initial velocity, crosses to the velocity after 1 year and diamonds to the velocity after I5 months.
Figure 5b shows calculated and measured velocity components along profile 1. There are three sets of velocity measurements available along this profile: summer 1997, summer 1998 and autumn 1998. The smallest root-mean-square (rms) error between calculated and measured surface velocities from these three measurement periods resulted in n = 3 and A = 23 × 10–16s–1kPσ–3 (Fig. 6). This optimal value of A is about three times smaller than the value recommended for temperate ice (Reference PatersonPaterson 1994, p. 96). It is, however, identical to the value of A = 23.7 × l0–16 s–1 KPσ–3 obtained by Reference GudmundssonGudmundsson (1999), and similar to the estimate of A = 20 × 10–16s–1kPσ–3 by Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others (1998) and the estimate of A = 22.2 × l0–16s–1kPσ–3 by Reference Albrecht, Jansson and BlatterAlbrecht and others (2000). Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others (1998), Reference GudmundssonGudmundsson (1999) and Reference Albrecht, Jansson and BlatterAlbrecht and others (2000) all arrived at their estimates for the rate factor using the same type of calibration process as is used here, i.e. by comparing measurements of surface velocities with calculations based on numerical flow models which incorporate horizontal stress gradients.
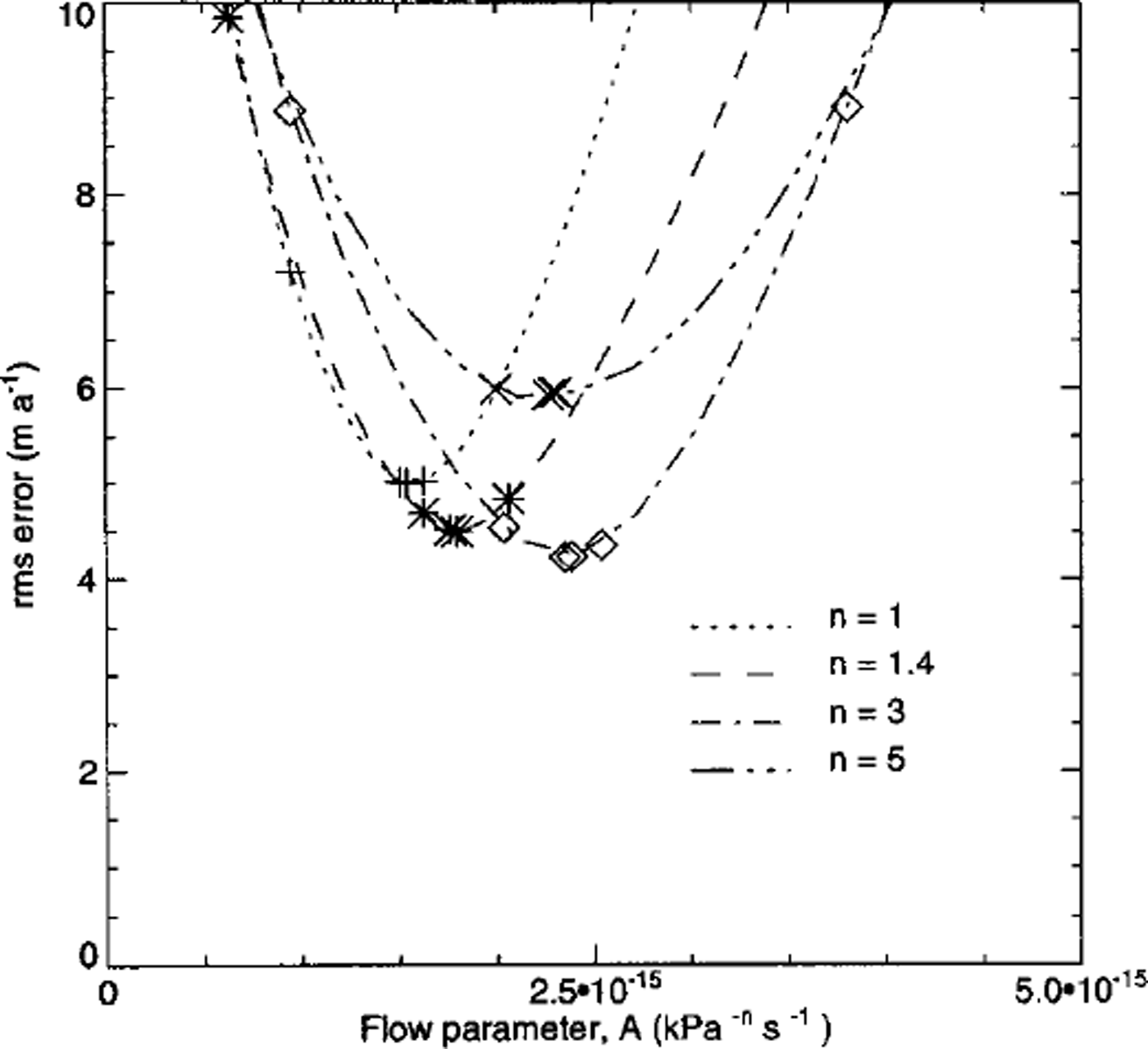
Fig. 6. The rms error between the measured and the modelled velocities for various n in the flow law, as a function of the flow parameter A.
The rms error between measured and modelled surface velocities is shown in Figure 6 as a function of A for a number of different values of n. The rms error is comparable to the measurement error in summer 1997 and summer 1998, but much larger than the errors of the measurements made in autumn 1998. Figure 7 shows modelled velocities plotted against measured stake velocities. Not all of the data points fall on a straight line with slope equal to one (shown as long dashes), indicating that there is not perfect agreement between measured and modelled velocities. The figure shows clearly that the deviations from this line are not randomly distributed. For example, modelled velocities after 12 and 15 months of forward integration are considerably smaller than measured velocities. Thus, the model is not free from systematic errors. It is difficult to pinpoint the cause for these. Some deviations are to be expected because the modelled cross-section is not exactly along a flowline.
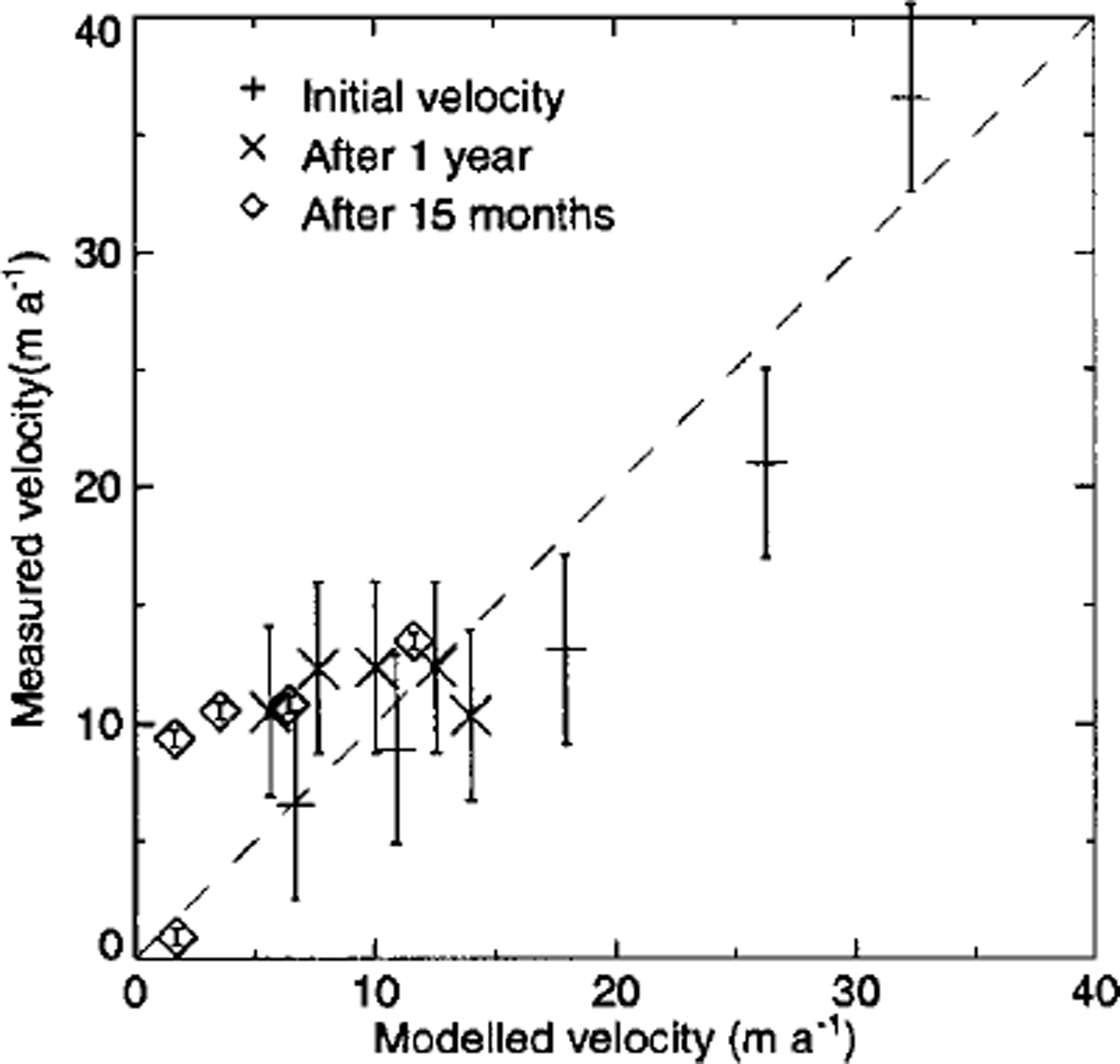
Fig. 7. The measured velocity plotted against the modelled velocity computed with n=3andA = 2.34 × 10–16 k P 6 a–3 6 S–1 .
Figure 8 shows the initial surface geometry (solid line), surface geometry after 15 months of forward integration (dotted line) and the resulting surface geometry after 15 years (dashed line). The measurements of the inital surface geometry (crosses) were not used in the tuning procedure. Therefore, the performance of the model with respect to transient changes in geometry can be judged by comparing the dotted curve with the crosses. Although not all the data points fall on the calculated curve, the depth at the centre of the canyon and the width of the canyon are reproduced with reasonable accuracy. The model performance is thus acceptable with respect to changes in geometry, but poor with respect to changes in surface velocities. This is understandable given the high sensitivity of modelled surface velocities to small variations in slope and ice thicknesses.
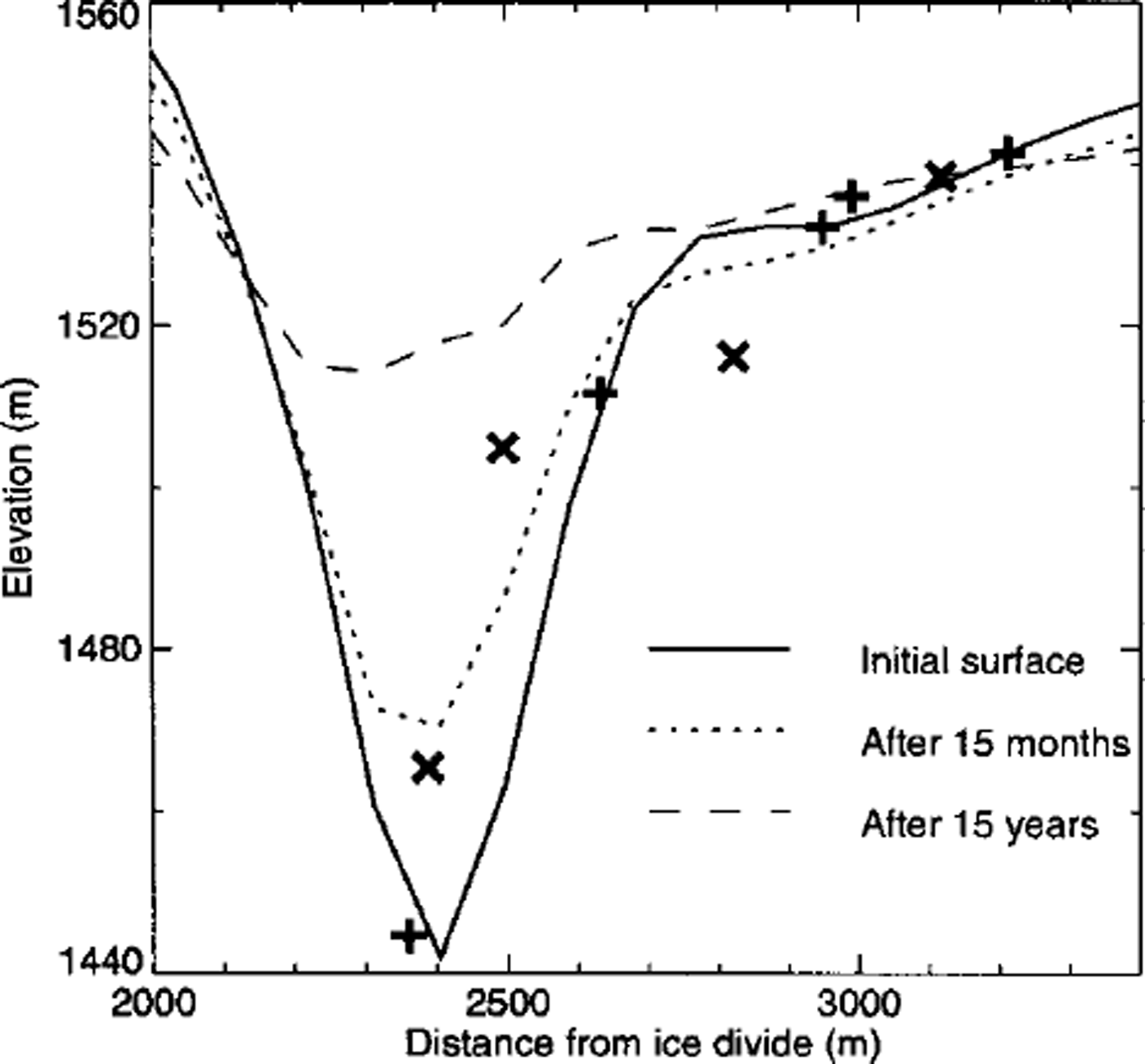
Fig. 8. Modelled andmeasured transient evolution of the surface along profilel for n = 3 and A = 2.34 × l0–16 kPa–3– S– 1 Crosses and plus symbols are measured elevations at the start of and 15 months after the start of the numerical simulation, respectively.
The initial surface geometry used in the model is not well constrained by measurements. The sensitivity of the modelled velocities and surface elevation to errors in initial surface elevation was estimated through a number of model runs. The deviation between observed and modelled quantities can be reduced significantly by adjusting the initial geometry of the model within the constraints given by measurements. It is possible that systematic errors can be largely, or even fully, eliminated in this way. Although it might improve the model performance, repeated trial-and-error adjustment of the initial surface geometry is not worthwhile and was not carried out. Further elevation measurements are needed in order to determine whether differences between measured and modelled surface velocities are caused solely by errors in surface geometry, and not by failures of some of the modelling assumptions.
5.3. Discussion of model results
The optimal value of the rate factor A is three times smaller than the value recommended by Reference PatersonPaterson (1994), but nevertheless in good agreement with results from two recently published studies (Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998; Reference GudmundssonGudmundsson, 1999). The estimated value of A would be even smaller if basal sliding, contrary to the model assumptions, significantly contributed to measured surface velocities. Changing the surface geometry of the model gives different estimates for the rate factor. Based on oblique photographs, we believe that the surface slopes of the model were underestimated. Increasing the surface slopes of the model would also lead to a smaller estimate for A
The model predicts that the depth at the centre of the canyon will be reduced to 10% of its initial depth after about 15 years. This result mainly depends on the overall magnitude of the velocities, and not on the finer details of the velocity profile along the surface. The changes in geometry are caused by diffusion of the initial thickness anomaly. The small surface slopes of the surrounding area ( ω1°), and the direction of the undisturbed flow along the axis of the canyon rather than perpendicular to it, both make the initiation of a kinematic wave impossible. This is a very different situation from that on the steeply sloped Drift Glacier, Alaska, where the 1966–68 eruptions of Mount Redoubt led to the triggering of a kinematic wave (Reference Sturm, Benson and MacKeithSturm and others, 1986).
The transient evolution of surface depressions on Vatnajökull having geometrical aspect ratios similar to those of the canyon have previously been modelled using the SIA Reference Gudmundsson, Raymond and BindschadlerQonsson and others, 1998). This modelling approach ignores the effects of horizontal stress gradients. We find that horizontal stress gradients have a very significant effect on the time evolution of the canyon. The calculated width of the canyon using the SIA after 15 months of forward integration is more than twice the measured width. Although the finite-element model did not predict surface velocities accurately, the agreement between observations and calculations is much better than for the SIA model. Surface velocities calculated with the SIA are at least one order of magnitude too large. A rough agreement with observed surface velocities can nevertheless be obtained by reducing the value of the rate parameter accordingly. The order-of-magnitude lower value for A than typically estimated for temperate ice, which Reference Jónsson, Adam and BjörnssonJónsson and others (1998) obtained, may result from the shortcomings of their SIA model.
6. Summary
Surface velocities and surface elevation along three transverse profiles with respect to the canyon were measured repeatedly over a period of about 2 years. The effect of the canyon on the flow velocities could only be clearly and unambiguously detected in one of these three profiles (profile 1). Most likely the canyon affects the flow along the other two profiles as well, but the effect is to a large extent masked by large-scale flow not related to the presence of the canyon.
The transient evolution of a Gaussian-shaped surface depression having geometrical ratios similar to those of the canyon was calculated using a series of different flow models. The transient evolution predicted by the SIA and that predicted by the kinematic-wave theory are essentially identical. Including horizontal stress gradients leads to significantly different predictions. Thus, the SIA cannot be used for modelling the diffusion of a surface disturbance with a spatial scale similar to that of the canyon. The inclusion of horizontal stress gradients is essential for obtaining a reasonably good approximation to solution of the full system.
Temporal changes in surface velocities and surface geometry along profile 1 were modelled using a two-dimensional finite-element model which solves for all the terms of the momentum equations. The model has two rheological parameters n and A which are constant in space and time. Values for these parameters were determined from a comparison between measured and modelled surface velocities. However, available measurements of elevation changes over time were not used for model calibration. For no pair of n and A could an agreement between measured and observed surface velocities be obtained which was free from systematic errors. Differences between measured and modelled surface velocities are, nevertheless, on the whole similar to estimated errors in the velocity measurements. The predicted changes in surface geometry over a 15 month period were also in reasonably good agreement with measurements. This agreement was obtained without any tuning. Estimating the sensitivity of the model with respect to changes in initial geometry revealed that further measurements of elevation changes over time are desirable for future model validation.
Acknowledgements
We acknowledge the logistical support of the Icelandic Glaciology Society (JÖRFi) during the fieldwork. We appreciate useful discussion with M.T. Gudmundsson, F. Palsson, and p. Hognadottir. G Leysinger did the finite-element calculation shown in Figure 4. Comments by T. Jόhannesson, U. H. Fischer and two anonymous reviewers significantly improved the clarity of the text. This work was supported by the National Research Council of Iceland (grant No. 10501) and the National Power Company of Iceland.










