Introduction
The influence of sea ice on the global climate has been assessed in the context of doubled CO2) experiments (e.g. Reference Spelman and ManabeSpelman and Manabe, 1984; Reference Dickinson, Meehl and WashingtonDickinson and others, 1987; Reference Washington and MeehlWashington and Meehl, 1986; Reference Ingram, Wilson and MitchellIngram and others, 1989). Simulation experiments conducted with global climate models (GCMs) generally indicate that CO2-induced warming will be amplified by the retreat and thinning of sea ice in the Arctic. As a result of these changes and concurrent changes in the snow cover on land, the magnitude of simulated global warming is enhanced considerably at high northern latitudes. Reasons for this enhanced temperature response are straightforward: ice and snow are highly reflective of solar radiation, and sea ice provides a substantial barrier to sensible and latent heat transfer between the ocean and the atmosphere. In interpreting the role of sea ice on Aritic and global climate as simulated by GCMs consideration of the physics included in sea-ice parameterizations is essential.
Presently, GCMs include a variety of different sea-ice parameterizations. While all of the models can be tuned to simulate accurately present-day sca-ice conditions, the response of each model to perturbations in forcing from the atmosphere or ocean differ substantially. To assess the possible impact of model approximations on the simulated climate, it is instructive to compare the sea-ice parameterizations used in climate simulations and sensitivity studies. In particular, a good understanding of how different ice models respond to heat- or momentum-flux perturbations at the ice atmosphere and ice-ocean interfaces is necessary.
To date, one-dimensional (1-D) slab thermodynamic sea-ice models (which do not include ice deformation) have most frequently been used in GCMs. The sensitivities of the 1-D sea-ice models to heat-flux perturbations have been explored in several studies. Reference Maykut and UntersteinerMaykut and Understeiner (1971) found that an increase of 5 W m−2 in the ice-ocean interfacial heat flux was sufficient to melt the ice completely during summer. Reference SemtnerSemtner (1984) compared the Reference Maykut and UntersteinerMaykut and Untersteiner (1971) sea-ice model to the 3 layer and 0 layer ice models presented in Reference SemtnerSemtner (1976) (see the next section). While the response of the equilibrium sea-ice thickness was the same for all three models, the phase and amplitude of the seasonal cycle of the 0 layer model was found to be in error because of its lack of storage of sensible and latent heat (e.g. brine pockets). Reference Shine and Henderson-SellersShine and Henderson-Sellers (1985) and Reference Curry, Schramm and EbertCurry and others (1993) conducted sensitivity studies that varied cloud properties, and found a large sensitivity of sea-ice thickness to cloud characteristics.
Several sensitivity studies to surface heat-flux perturbations have also been conducted using two-dimensional (2-D) dynamic-thermodynamic sea-ice models. Reference HiblerHibler (1984) found that, in terms of areal ice extent, thermodynamics-only and dynamic-thermodynamic models were equally sensitive to warming perturbations. However, in terms of changes in the ice thickness, the dynamic-thermodynamic model showed less sensitivity than the thermodynamic-only model. This was due in part to the negative feedback of leads in the dynamic model, as more winter freezing occurs when the lead fraction is higher, resulting in higher average ice thickness. Also, mechanical buildup of ice was found to dominate over thermodynamic considerations for regions of high ice convergence. Additional sensitivity studies using 2-D dynamic-thermodynamic models have been performed by Reference Holland, Mysak, Manak and OberhuberHolland and others (1993), Reference Maslanik and SilcoxMaslanik and Silcox (1993), Reference Chapman, Welch, Bowman, Sacks and WalshChapman and others (1994) and Reference Fischer, Lemke, Jo-hanncssen, Muench and OverlandFischer and Lemke (1994).
Previous sensitivity studies have been conducted using very different experimental designs, and it is difficult to draw conclusions based upon these results, particularly concerning the differences in the physics included in the different models. In the present study, the sensitivities of a variety of sea-ice models to external heat-flux perturbations are examined in a systematic way, following the general experimental design used by Reference Curry, Schramm and EbertCurry and others (1995). Separate experiments are conducted to compare the response of each model to heat fluxes applied at the atmospheric interface vs the oceanic interface. The intercomparisons of the response of different models are interpreted in the context of the physical paramcterizations used in each of the models. Recommendations are made for the parameterization of sca-ice processes in climate models; the accuracy requirements for observations and parameterization of the surface heat-flux components are also addressed.
Description of the Model
A total of six different sea-ice models are compared in this study. These models include those that are generally available (e.g. Reference SemtnerSemtner, 1976; Reference HiblerHibler, 1979; Reference Flato and HiblerFlato and Hibler, 1992; Reference Ebert and CurryEbert and Curry, 1993). Additionally, we include results from two new sea-ice models developed by our research group and described by Reference Schramm, Holland and CurrySchramm and others (in press) and Reference Hibler, Hansen and TakahashiHolland and others (1997).
Reference SemtnerSemtner (1976) developed a 1-D thermodynamic sea-ice model that simplified the formulation of Reference Maykut and UntersteinerMaykut and Untersteiner (1971). The conductivity of ice is assumed to be constant with temperature and salinity. Penetrating solar radiation for snow-free ice is stored in a heat reservoir representing internal melt water, instead of immediately melting the surface ice. In autumn, the surface temperature is not allowed to drop below freezing until this reservoir is exhausted, thus retarding surface cooling.
The Reference SemtnerSemtner (1976) 3 layer model has two internal ice temperatures and one internal snow temperature. The Reference SemtnerSemtner (1976) Olayer model has no separate snow and ice layers, although snow is still allowed to accumulate. Because the assumption of a linear temperature profile within the ice would cause the ice to become too thick, the conductivities of snow and ice are increased. To compensate for a lack of brine pockets, which would retard surface cooling, a fraction of what would be penetrating solar radiation in the 3 layer model is applied as surface energy flux while the remainder is reflected away.
Reference Ebert and CurryEbert and Curry (1993) presented a 1-D thermodynamic sea-ice model that includes 10 internal ice temperatures. New features relative to the Reference Maykut and UntersteinerMaykut and Untersteiner (1971) model include surface meltwatcr ponds of variable area and depth during the summer melt season, as well as a sophisticated treatment of leads including lateral freezing and melting. There is a specified export of ice, and the lead fraction evolves with time. Finally, the model has a more complex treatment of surface albedo that includes five surface types and four spectral intervals.
The model developed by Reference Schramm, Holland and CurrySchramm and others (in press) is a single-cell ice-thickness distribution model; it is a Lagrangian model following an aggregate ice-thickness distribution with a horizontal extent that can, in principle, range from 20 to 500 km. This model has similar thermodynamic features to the Reference Ebert and CurryEbert and Curry (1993) model. In addition, the model includes an ice-thickness distribution, ridging and export. These parameters, while similar to Reference BjórkBjórk (1992), are complicated considerably by including multiple internal layers in the ice. Sea ice is resolved by a number of classes characterized by various properties, including thickness and age. Both an open-water category and several ridged-ice categories are included in the distribution. Penetration of solar radiation is affected by the fractional area of melt ponds and the number of layers. There is enhanced absorption in the uppermost 10 cm of the ice.
In the simulations used here, a “slab” ocean mixed-layer model (Reference Holland, Curry and SchrammHolland and others, in press) is used with the Reference Maykut and McPheeMaykut and McPhee (1995) parameterization of the ice-ocean turbulent flux. The model described by Reference Hibler, Hansen and TakahashiHolland and others (1997) is similar to the Reference Schramm, Holland and CurrySchramm and others (in press) model except that it contains different parameterizations of dynamical processes. A mechanical redistribution function based on Reference Thorndike, Rothrock, Maykut and ColonyThorndike and others (1975), Reference RothrockRothrock (1975) and Reference HiblerHibler (1980) is used, which is consistent with a plastic rheology. This allows thin ice to he compressed into thick pressure ridges and open water to be produced under divergent or shearing ice conditions. The model dynamics is driven by strain-rate data obtained from the Arctic Ice Dynamics Joint Experiment (AIDJEX) (Reference ColonyColony, 1978).
The Reference HiblerHibler (1979) 2-D dynamic-thermodynamic sea-ice model includes a thermodynamic component similar to the Reference SemtnerSemtner (1976) 0 layer model. The dynamic component of the model includes a momentum balance of air stress, water stress, Coriolis force, internal ice stress, inertial force and ocean tilt. It features a constitutive law relating ice stress to strain rate. The ice is assumed to be rigid-plastic for normal deformation rates, but acts as a linear viscous fluid for small deformation rates. There is a simple ice-thickness distribution of two classes: thick ice and open water. The open-waler class also includes thin ice of <50cm. Open water is created under divergent conditions and removed under convergent conditions, but total ice mass is conserved within each grid-cell. Finally, ire strength is parameterized as a function of thickness and the fraction of open water.
Reference Flato and HiblerFlato and Hibler (1992) presented a dynamic model similar to Reference HiblerHibler (1979), but with a simpler constitutive law. Here, the ice is assumed to act as a cavitating fluid, having compressive strength but no shear strength.
Model Response to Surface Heat-Flux Perturbation
Surface heat-flux perturbations at the ice-atmosphere interface may, in principle, arise from many different sources. In a CO2 doubling scenario, the most direct surface heat-flux perturbation is in the longwave surface flux, although as a result of atmospheric feedback processes, perturbations are likely to arise in the other surface flux components as well. At the ice-occan interface, changes in the heat flux may arise from changes in the heat entrained or diffused into the ocean mixed layer from the deeper ocean. Recent observations by Reference AagaardAagaard and others (1996) found Atlantic layer temperatures 0.5-1.0°C warmer than previously measured. A temperature increase such as this might subsequently increase the heal flux at the bottom of the ice.
In this section, the responses of the different sea-ice models to surface heat-flux perturbations are examined. We attempt to use these models in a manner as close to their standard format as possible. Rather than using the same set of forcings for all of the models, each was used with its standard datascet. This results in slightly different baseline average ice thicknesses for each model (Tables 1, 2 and 3). Although sensitivity experiments are sensitive to initial conditions, it was felt that this methodology was preferable to “tuning” either the models or the forcing.
Table 1. Surface longwave and ocean heat-flux perturbations necessary to melt sea ice completely during summer for 1-D thermodynamic slab models (W m−2). Baseline mean annual thickness (cm) is also given

Table 2. Surface longwave and ocean heat-flux perturbations necessary to produce a maximum summertime open water fraction for single cell ice-thickness distribution models (W m−2). Baseline mean annual thickness (cm) is also given
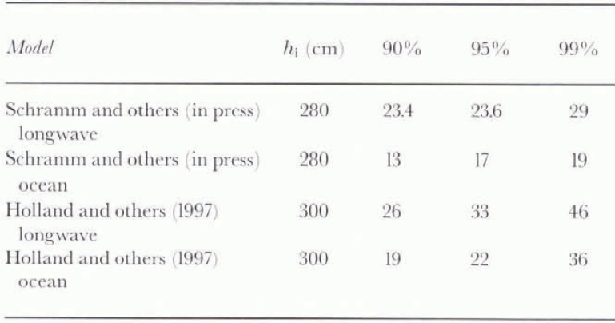
Table 3. Surface longwave and ocean heat-flux perturbations necessary to produce a maximum summertime open-water fraction for 2-D dynamic-thermodynamic models (W m−2). Baseline mean annual thickness (cm) is also given

The heat-flux perturbation at the upper ice surface is Specified to be a change in the longwave radiation flux, while the flux perturbation at the lower ice surface is specified to be a change in heat flux into the ice underside. Both are applied uniformly over the annual cycle. The heat flux is increased in sequential model runs until some threshold condition, depending on the model, is reached. The perturbations required for each model to reach these conditions are then compared.
The threshold conditions for intercomparison depend on the model type. The
simulations using 1-D slab models (i.e. Reference SemtnerSemtner, 1976; Reference Ebert and CurryEbert and Curry,
1993) are run for 100 years. Because some of the models produce a
multi-year equilibrium cycle whereby ice may disappear only once in a cycle
lasting several years, the threshold is defined as the ice having zero
thickness for a period of
![]() 1 day in at least 10 of the last 20 years of the model run.
We note that this definition is somewhat different than that used by Reference SemtnerSemtner (1976) and Reference Curry, Schramm and EbertCurry and others (1995). For the single-cell ice-thickness
distribution models and the 2-D dynamic-thermodynamic models, maximum
open-water fraction rather than ice thickness is used as the threshold, so that
the results are not biased by the very large amount of heat required to melt
the thickest ridged ice. The 1-D models consider a typical area in the central
Arctic, while the 2-D simulations consider a regional average of the central
Arctic Ocean. This region, as defined in Reference Gloersen, Campbell, Cavalieri, Comiso, Parkinson and ZwallyCloersen and others (1992), includes the Beaufort, Chukchi, and
Laptev Seas but excludes the Kara and Barents Seas and the Canadian Archipelago
(however, the model simulation includes the entire Arctic Ocean, all of the
peripheral seas, and the Greenland, Iceland and Norwegian Seas).
1 day in at least 10 of the last 20 years of the model run.
We note that this definition is somewhat different than that used by Reference SemtnerSemtner (1976) and Reference Curry, Schramm and EbertCurry and others (1995). For the single-cell ice-thickness
distribution models and the 2-D dynamic-thermodynamic models, maximum
open-water fraction rather than ice thickness is used as the threshold, so that
the results are not biased by the very large amount of heat required to melt
the thickest ridged ice. The 1-D models consider a typical area in the central
Arctic, while the 2-D simulations consider a regional average of the central
Arctic Ocean. This region, as defined in Reference Gloersen, Campbell, Cavalieri, Comiso, Parkinson and ZwallyCloersen and others (1992), includes the Beaufort, Chukchi, and
Laptev Seas but excludes the Kara and Barents Seas and the Canadian Archipelago
(however, the model simulation includes the entire Arctic Ocean, all of the
peripheral seas, and the Greenland, Iceland and Norwegian Seas).
Since the intention of these experiments is to compare the responses of different sea-ice models to surface heat-flux perturbations, it is acceptable to ignore ice atmosphere and ice ocean feedbacks as the ice conditions change. While these feedback processes are of fundamental importance to understanding and modeling the response of the coupled climate system to a heat-flux perturbation, their inclusion in the present study would unnecessarily complicate our interpretation of the first-order response of the sea ice. However, some processes are intrinsic within the model physics, and therefore cannoi be eliminated. For instance, in the models with an open-water fraction associated with leads (i.e. all but the two Semtner models), a slab ocean mixed-layer model is included. This results in the inclusion of the lead-solar flux feedback (e.g. Reference HiblerHibler. 1981; Reference Ebert and CurryEbert and Curry, 1993), whereby heat entering the ocean contributes to warming of the mixed layer and greater basal ablation. without including this feedback, energy would not be conserved in models that have leads. Also included in all except the two Semtner models is the surface turbulent flux feedback, whereby the sensible and latent heat fluxes at the atmosphere interface are calculated at each time-step as a function of ice surface temperature. Thus, changes in surface temperature due to longwave or ocean heat-flux perturbations will also affect the sensible and latent heat fluxes, resulting in a small negative feedback (e.g. Reference Ebert and CurryEbert and Curry, 1993).
Results for the various 1-D thermodynamic slab models are summarized in Table 1. Comparison of the Semtner 3 layer and 0 layer simulations shows that the approximations made to the heat conduction in the 0 layer model reduces somewhat the sensitivity of the model to a heat-flux perturbation. Relative to the Reference SemtnerSemtner (1976) models, the Reference Ebert and CurryEbert and Curry (1993) model shows a Substantially increased sensitivity. This increased sensitivity arises from the strong ice-albedo feedback mechanism in this model due to the inclusion of melt ponds (e.g. Reference Curry, Schramm and EbertCurry and others, 1995) and from the lead solar-lux feedback.
The results from the single-cell thickness-distribution models are given in Table 2 for maximum open-water fractions of 90%, 95%, and 99%. Complex feedbacks within the model give rise to an oscillatory response to heat-flux perturbations where the maximum open-water area ranges from <40% to >90%. In comparison with the 1-D thermodynamic sea-ice models, the heat-flux perturbations required by the single-cell ice-hickness distribution are an order of magnitude larger than the values for the Reference Ebert and CurryEbert and Curry (1993) model and approximately a factor of two larger than values for the Reference SemtnerSemtner (1976) models, clearly illustrating the role that ridging and the ice-thickness distribution has in decreasing the sensitivity of sea ice to a heat-flux perturbation. Ridging creates open water, resulting in increased first-year ice production in winter and a negative feedback to the decreasing ice thickness.
The Reference Hibler, Hansen and TakahashiHolland and others (1997) model shows a decrease in the sensitivity to heat-flux perturbations compared to the Schranun and others (in press) model. This is due to a combination of different ridging parameterization and different dynamical forcing, which creates a larger areal percentage of ridged ice in the Reference Hibler, Hansen and TakahashiHolland and others (1997) model than in the Reference Schramm, Holland and CurrySchramm and others (in press) model. Thus, more heat is required to melt the ice.
Table 3 presents results from the 2-D dynamic-thermodynamic models. While a direct comparison of the Reference SemtnerSemtner (1976) 0 layer results with the Reference HiblerHibler (1979) and Reference Flato and HiblerFlato and Hibler (1992) results cannot be made here because of differing experimental designs, it is apparent that inclusion of full 2-D ice dynamics decreases substantially the sensitivity of sea-ice models to heat-flux perturbations (this was also noted by Reference HiblerHibler, 1984). Prevailing winds cause a buildup of thick ice along the north Greenland coast and Canadian Archipelago (Reference HiblerHibler, 1979; Reference Flato and HiblerFlato and Hibler, 1992), and ice in the central basin melts long before the ice along these coasts. Details of the ice theology are shown to be important in the comparison between the Reference HiblerHibler (1979) and Reference Flato and HiblerFlato and Hibler (1992) models. While the necessary heat-flux perturbations for 60% and 70% open water are nearly identical, the results begin to diverge for the 80% open-water case. The viscous-plastic rheology (Reference HiblerHibler, 1979) produces a larger region of thicker ice along the Canadian Archipelago than the cavitating-fluid rheology (Reference Flato and HiblerFlato and Hibler, 1992). As was the case in the single-cell models with ridged ice, this thicker ice requires a larger heat-flux perturbation to melt.
For each model, a smaller perturbation of ocean heat flux was required to produce the same result as its corresponding longwave heat-flux perturbation (Tables 1, 2 and 3). This arises because icemelt at the ice-atmosphere interface occurs only dining the summer melt period, even in the presence of a large heat-flux perturbation, while a phase change at the ice-ocean interface can occur throughout the year if the ocean heat fluxes are large enough. The rat to of the longwave heat-flux perturbation to the ocean heat-flux perturbation is smallest for the Reference Ebert and CurryEbert and Curry (1993), Reference Schramm, Holland and CurrySchramm and others (in press) and Reference Hibler, Hansen and TakahashiHolland and others (1997) models because of the inclusion of melt ponds, which enhances the ice-albedo feedback.
Summary and Conclusions
This study has emphasized the differences among different sea-ice models in their response to surface heat-flux perturbations. As was noted by Reference HiblerHibler (1984), inclusion of ice dynamics decreases substantially the sensitivity of a sea-ice model to heat-flux perturbations. The strong ice-albedo feedback mechanism included in the Reference Ebert and CurryEbert and Curry (1993) model increases the sensitivity relative to the other 1-D models. The single-cell ice-thickness distributor models show sensitivities that are intermediate to the 1-E and 2-D models. Although this study has included only a selection of sea-ice models, it seems likely that the Reference Ebert and CurryEbert and Curry (1993) model bounds the existing models on the high-sensitivity end, while the Reference HiblerHibler (1979) model bounds the population of existing models on the low-sensitivity end. To date, most GCM simulations of a CO2 doubling scenario have used a sea-ice model similar to the Reference SemtnerSemtner (1976) 0 layer model. As the Reference HiblerHibler (1979) and Reference Flato and HiblerFlato and Hibler (1992) models and their variants are used increasingly in climate models (e.g. Reference Pollard and ThompsonPollard and Thompson, 1994; Reference Meehl and WashingtonMeehl and Washington, 1995), the simulated sensitivity of the climate in high northern latitudes to a CO2 doubling will undoubtedly decrease significantly.
It remains a major challenge in sea-ice modeling to reconcile the complex physics involved in ice dynamics and thermodynamics in a single model that can realistically determine the response of sea ice to a climate-change scenario. An optimal model to reproduce the actual response of sea ice to a surface heat-flux perturbation, based upon our present understanding of sea-ice dynamics and thermodynamics, would include the dynamics of the Reference HiblerHibler (1979) model plus the effects of an ice-thickness distribution (Reference Flato and HiblerFlato and Hibler, 1995; Reference Hibler, Hansen and TakahashiHolland and others, 1997), along with the thermodynamics described by Reference Schramm, Holland and CurrySchramm and others (in press). Because of the non-linear processes that occur within sea-ice models, the sensitivity of such a combined model cannot be anticipated from the results presented here. Additionally, there are uncertainties in our understanding of some aspects of sea-ice processes, notably surface processes that determine the albedo and the thermodynamics and dynamics associated with ridged ice. It is anticipated that the Surface Heat Budget of the Arctic Ocean (SHRBA) experiment will address some of these uncertainties (SHEBA Science Working Group, 1994).
The results presented here also place some bounds on observational and modeling requirements for the net heat flux at the top and bottom surfaces of the ice. It seems that, as an upper bound, the accuracy of observed net fluxes should be less than half of the modeled values required to obtain ice-free conditions. For example, if 30 W m−2 is required to melt the ice from above, a measured accuracy of 15 W m −2 would be needed. GCMs currently do not approach this accuracy for fluxes at the atmospheric interface, nor do satellite observations (e.g. Reference Curry, Pinto, Benner and TschudiCurry and others, 1997). The present study suggests that the modeling and observational requirements may be even more stringent for the ice-ocean fluxes.
Feedback processes between the sea ice, atmosphere and ocean undoubtedly influence the sensitivity of sea ice to a surface heat-flux perturbation. Until improved sea-ice para-meterizations are included in global climate models, along with accurate parameterization for the interfacial fluxes between the ice atmosphere and ice ocean, the influence of sea ice on the global climate will remain uncertain. Additional work is needed to define further the key processes and level of complexity required for sea-ice treatments in GCMs.
Acknowledgements
We wish to thank G. Flato, M. Harder, and J. Richter-Menge for their comments and suggestions while reviewing this paper. This research was supported by NSF OPP-9504261.





