Snowmelt modelling on signy island, South Orkney Islands

Abstract

The ability of the Utah energy-balance and snowmelt model (UEB) to simulate decline in snow water equivalent (SWE) at an extreme location was assessed. Field data were collected at Paternoster Valley, Signy Island, South Orkney Islands (60°43′S) during the austral summer of 1996–97. This is the first application of UEB in a maritime Antarctic site. UEB is a physically based snow melt model using a lumped snow-pack representation with primary state variables SWE and snow pack-energy content (U). Meteorological inputs are air temperature, wind speed, humidity, precipitation and total incoming solar and longwave radiation. The Paternoster Valley catchment was subdivided into eight non-contiguous terrain classes for sampling and modelling using a geographical information system (GIS). Simulations of SWE in each of these classes were compared พ with field observations. It is shown that initial U and snow-surface thermal conductance (K_s) affect model simulations. Good approximations of SWE depletion are obtained using measured incoming solar radiation to drive the model but there are shortcomings in the characterization of long wave radiation and sensible-heat fluxes.

1. Introduction

The development of distributed snowmelt modelling has seen increased use of energy-balance snowmelt models (Kirnbauer and others, 1994) which parameterize snow-surface energy fluxes with physically based equations. In most cases, snowmelt models are applied at a point and results distributed throughout the catchment (Blöschl and others, 1991a, b; Ranzi and Rosso, 1991; Flerchinger and Cooley, 1992; Sambles and Anderson, 1994; Tarboton and others, 1995a).

Model performance at any location depends upon the heterogeneity of the catchment and the choice of site for parameter calibration. The latter depends on the method of catchment subdivision employed (if any) for the spatial distribution of model results. Commonly, study areas are divided into gridcells derived from a digital elevation model (Blöschl and others, 1991a; Flerchinger and Cooley, 1992) or “homogenous” areas based upon topographic attributes (Sambles and others, 1990; Harrington and others, 1995b). Model performance can be assessed by comparing simulations with observations of snow-covered area (SCA) (Blöschl and others, 1991a, b; Harrington and others, 1995a) or snow water equivalent (SWE) (Braun, 1991; Elder and others, 1995; Rovansek and others, 1993; Tarboton and others, 1995a). However, the measurement of SWE is not straightforward (Elder and others, 1991; Rovansek and others, 1993). It is therefore appropriate to test the suitability of an Alpine-developed snowmelt model for use in extreme conditions (the maritime Antarctic) to simulate SWE decline during the thaw.

The Utah energy-balance snow accumulation and melt model (UEB) (Tarboton and Luce, 1996) was chosen in preference to other available snowmelt models such as SNTHERM (Jordan, 1991) for its simplicity and transportability. It has been field tested and validated in Alpine areas (Harrington and others, 1995a; Tarboton and others, 1995a, b) but not other climatic regimes. Its features include a lumped snowpack representation, minimal calibration requirements and readily available driving inputs. In the absence of all necessary meteorological data, components of the snow-surface energy balance are estimated from the daily air-temperature range. UEB then becomes a “hybrid” energy-balance/temperature-index model. There is at present little work on validating the effectiveness of Alpine energy-balance snowmelt models at high latitude (Rowe and Kuivinen, 1995) or sub-polar sites.

In a wider context, UEB represents the quantity component of a developing snowmelt quantity-quality modelling scheme for the maritime Antarctic, for assessing nutrient delivery during the thaw. The aims of the work are:

• (1) To test the suitability of a state-of-the-art snowmelt model (UEB) in a maritime Antarctic catchment.

• (2) To simulate SWE decline in a range of terrain classes, defined by a geographical information system (GIS) subdivision of the catchment.

• (3) To determine model response to initial parameter values and to identify those that require field calibration.

This paper presents the results of applying UEB to Paternoster Valley, Signy Island, for the 1996–97 melt season. Field and GIS methods are described, simulated and observed SWE for a scries of snow pits are compared and the choice of initial parameter values discussed.

2. Field Site

Signy Island (60°43′ S, 45°38′ W) is situated in the South Orkney Islands, maritime Antarctic (Fig. 1). The region is characterized as having a moister climate than continental Antarctica whilst still within the limit of winter sea-ice development (Smith, 1984). The study catchment, Paternoster Valley, is on the northeast side of the island and has been the subject of previous lake and stream hydrochemistry studies (Light 1976; Hawes, 1983, 1985). Total catchment area is 8.4 km², of which 6% is open water and 10% is permanent snow and ice. Elevation extends from sea level to a maximum of 204 m. The area contains terrain with a wide variety of slope (0–75°) and aspect (0–359°). Cliffs border the northern and southern margins and there is a broad, Hat col to the west. The sparse vegetation consists of patches of moss and lichen on exposed bedrock and talus.

Fig. 1. Location map for Paternoster Valley, Signy Island, showing the automatic weather station and field snow-pit locations.

Mean annual air temperature is −3°C (Appleby and others, 1995). 20 years of records indicate that mean annual precipitation (rain and snow) is 268 mm year⁻¹ falling over approximately 270 days (unpublished data from the British Antarctic Survey). Cloud cover averages 7 oktas (Rootes, 1988). The snowfall period lasts from late-March until mid-December each year, with snow depths of up to 200 cm present in Paternoster Valley in late-October (Walton, 1987). There is normally a basal ice layer 3–5 cm thick beneath the seasonal snowpack which develops each year from August onwards (personal communication from A. Caulkett, 1996). This was present throughout Paternoster Valley in late-October 1996 and promotes rapid meltwater drainage to the stream and three lakes within the catchment.

3. The Snowmelt Model

UEB is an energy-balance snowmelt model using a lumped snowpack representation (Tarboton and others, 1995b). Primary state variables are SWE (m) and snowpaek-energy content U(kJ m ⁻²), the latter relative to the reference state of ice at 0°C. U is defined as the energy content of the snowpack plus a top layer of soil with depth D_e(m). A value of U> 0 indicates an isothermal snowpack with some liquid-water content while U< 0 is used to calculate snowpack average temperature below 0°C.

Albedo is used as a third-state variable and is calculated as a function of snow-surface age (τ) and solar-illumination angle using the BATS albedo routines (Dickinson and others, 1993). F_age accounts for snow-surface ageing and is incremented at each time-step. It is defined as

(1)

where τ is the non-dimensional snow-surface age. New snowfall greater than 1 cm is assumed to return τ = 0.

An equilibrium approach to snow-surface temperature (T_s) is employed. Energy-balance equations are linearized about a reference temperature T* and an iterative method is used to solve T_s . If the final T_s < 0°C, it is used to calculate the energy fluxes at the snow surface. If T_s > 0°C, the snow-surface energy input cannot be balanced by thermal conduction into the snowpack and surface melt will occur. The infiltration of meltwater is used to balance the energy equation and T_s is set to 0°C.

Driving inputs are total incoming solar radiation, incoming longwave radiation or air temperature. If incoming solar-radiation data are unavailable, they are estimated as an extra-terrestrial radiation multiplied by an atmospheric transmission factor T_r , approximated from the diurnal air-temperature range (Bristow and Campbell, 1984). If incoming longwave radiation data are unavailable, they are estimated from air temperature, the Stefan—Boltzmann equation and a parameterization of air emissivity (Satterlund, 1979) adjusted for cloudiness with T_r . This is given as

(2)

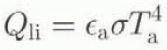
where Q_li is the incoming longwave radiation (W m ⁻²), is the air emissivity, σ is the Stefan-Boltzmann constant (5.669 × 10 ⁻⁸ W m⁻² K⁻⁴), T_a is the air temperature (K).

Outgoing longwave radiation (Q_le ) is given as

(3)

where T_s is the snow-surface temperature (K). Snow-surface thermal conductance, K_s (analogous to heat and vapour conductances), is defined as

(4)

where K is the snow thermal diffusivity (m²s⁻¹) and Z _e is the depth over which the temperature gradient acts (m).

For all model runs, a 2 hour time-step was used, precipitation inputs were ignored and ground heat flux was assumed to be zero. An initial snow surface age of 0.5, new snow albedo of 0.85 and a thermally active soil depth (D₍ ) of 0.2 m were used. The effects of varying initial snow-energy content (U₀) and K_s were investigated. Driving inputs were either total incoming solar radiation or air temperature, the latter adjusted for snow-pit elevation using a lapse rate of 1°C per 100 m. All other values were as recommended by Tarboton and Luce (1996). A summary of field inputs is given in Table 1.

Table 1. UEB field-input requirements

4. Model Application

Catchment subdivision

A digitized contour map of Signy Island was converted into a 25m digital elevation model (DEM) using the GRID module of the ARC/INFO GIS (Environmental Systems Research Institute, 1993). The watershed of Paternoster Valley was demarcated using flow-direction data obtained from the DEM. Grids of elevation, aspect and slope were combined and clustered using an isodata approach. A maximum likelihood classifier was applied to sort each cell into one of eight “homogenous”, non-contiguous terrain classes. The number of classes was constrained by fieldwork capabilities. The cell with topographic attributes closest to the class mean was chosen as a sampling site (Table 2). This allowed representative measurement of snowpack characteristics to be made for each class.

Table 2. Topographic attributes of terrain-class sites derived from the GIS (see section 4) and measured at the field location (terrain classes 2, 7 and 8 were not sampled)

Field data

The study period extended from late-October 1996 to early-January 1997. Snow cover was less than the seasonal average in late-October and large areas of the catchment were snow-free. Field-sampling sites were located using map, compass and altimeter (Fig. 1). A snow pit was dug at each (where possible) and a fresh pit face excavated on each visit. Snow pit 5 was sited on a snow patch in an otherwise snow-free terrain class, while pit 6 was at a topographic high point in an area of permanent snow. Three snow pits were not sampled. Snow pit 2 was deemed unsafe to approach while pits 7 and 8 (on the eastern slopes) were snow-free due to wind scour. It is estimated that less than 1 % of the total SWE was contained in these three classes at the beginning of the fieldwork period.

Snow density was measured for surface and basal snow, using cores taken with a metal tube (volume 1295 cm ⁻³) inserted into the snow-pit wall. Density was recorded as the mean value of three such cores. Mean surface density was 468 kg m ⁻³, mean basal density 506 kg m ⁻³ and all measurements were within 15% of the respective mean value. Overall snow density for all pits over the melt season, as required for model runs, was 484 kg m⁻³. Snow depth was measured with a metal snow probe at each pit. It was also measured at four locations 2 m away from the pit in cardinal directions (defined relative to the line of maximum slope) to minimize surface-roughness effects. Recorded depth was the mean of these five values. SWE was calculated for each pit using mean seasonal snow density and mean snow depth. Precipitation falling as snow during the sampling period was less than 3 cm. A coarse snowpack surface crust in late-October minimized wind scour. Drifting of fresh snowfall occurred only in topographic hollows and not in exposed snow-pit locations.

Meteorological measurements were made using an automatic weather station (AWS) and a Campbell 21X logger located in the centre of the catchment at 40 m a.S.l. (Fig. 1). Point measurements of air temperature, relative humidity and total incoming solar radiation were logged at 15 minute intervals. Recorded wind speed and direction were the mean of a 5 minute sample period, logged every 15 minutes. Incoming longwave radiation was not measured and no cloud-cover data were available. Another AWS was located on Jane Col, to the southwest ofthe catchment at 150 m a.S.l. Missing data from the Paternoster Valley AWS were esti-mated by applying transfer functions to the Jane Col data-set. This amounted to the first week of the modelling period only (Julian days 309–315, inclusive). During the study period, mean air temperature was + 1.07°C and mean diurnal air-temperature range was 4.65°C. Total incoming solar radiation reached a peak of 893 W m ⁻² (Fig. 2). The prevailing northwesterly wind had a mean speed of 4.1 m s⁻¹.

Fig. 2. Summary of meteorological data. Paternoster Valley, Signy Island; austral spring 1996. (a) air temperature. (b) mean diurnal air-temperature range, and (c) total incoming solar radiation.

5. Model Simulations

Results of SWE simulations are presented lot five snow pits during the 1996–97 melt period. A summary of physical variable and parameter values is given in Table 3. Figure 3 shows simulations driven by measured incoming solar radiation using U ₀ and K_s values of 5000 kJ m₋₂ and 2.8 × 10⁻⁶ m s ⁻¹, respectively. In the absence of field calibration of these parameters, values were obtained by fitting model simulations to observed SWE. U₀ was checked to ensure that a melt rate was produced within the seasonal range of values. This is acknowledged as a poor method of initializing physical parameters and they do not represent optimized values. As such, the simulations are no indication of model performance and merely illustrate UEB as being capable of SWE simulation.

Table 3. Parameters and physical variable values for UEB application in Paternoster Valley, Signy Island

Fig. 3. Simulated and observed SWE for Paternoster Valley, Signy Island; austral spring 1996, using solar radiation as the driving input. Solid lines represent simulated SWE; dots denote observed SWE.

Predictions closely approximate field observations at four of the five sites but SWE decline was underestimated at snow pit 6. A better simulation for this pit was obtained using air-temperature-derived radiation fluxes to drive the model (Fig. 4). The absence of field data for the incoming longwave radiation component ofthe energy balance resulted in UEB estimating this from air temperature as described in section 3. In such eases, the model takes on a “hybrid” form using both energy-balance and temperature-index methods. This accounts for differences in model simulations with driving input.

Fig. 4. Comparison of simulated SWE (solid lines) and observed SWE (dots) for snow pit 6, using measured total incoming solar radiation and air-temperature estimated radiation as driving meteorological inputs.

Longwave radiation is a key energy-balance component at sub-polar sites, line to cloud cover and advection influences (Hodson and others, in press). The estimation method may therefore have significant impact on the ability of UEB to simulate SWE, decline in the maritime Antarctic. Temperature-based estimates are not particularly applicable to such sites but are the best available option. The small areal variability in observed ablation (approximately 25–30 cm SWE front Julian days 309–339) suggests that longwave radiation is a more important influence than solar radiation in the surface-energy balance.

Sensible-heat flux may also be difficult to estimate if a strong temperature gradient exists near the snow surface. UEB uses neutral turbulent-transfer coefficients which may poorly characterize surface-buoyancy effects. The high elevation of snow pit 6 (with greater wind exposure) and improved simulations obtained using a temperature-index approach could indicate a better characterization of sensible-heat transfer with this method at that site.

The value of U₀ determines the snowpack liquid-water content, since the liquid fraction is derived from the snow-pack-energy content. U₀ = 5000 kJ m⁻² equates to a snow liquid-water content of between 1.7% and 5.5%, depending on snow depth. UEB defines the snowpack liquid-water holding capacity as 5%. It is possible to measure U₀ but this was not done during the field season. However, the calculated values would indicate no melt water outflow in late-October 1996, which corresponds with observations. Results were also sensitive to snow-surface thermal conductance (K_s) designed to be used as a “tuning parameter” (Tarboton and Luce, 1996). Approximating K_s as 2.8 × 10⁻⁶ m s^-1 gave the best SWE simulations. This low value can be attributed to coarse surface snow (grain-size 2–3 mm) evident at the start of the melt period.

Snow-surface age increased from its initial value of 0.5–9.3 (dimensionless), reflecting the exclusion of new snow accumulation in model runs realistically. It should be returned to zero after each new snowfall. This affected calculations of snow-surface albedo which declined from 0.85 to 0.50. However, these two variables did not affect simulated SWF, decline.

UEB does not lend itself to detailed simulation ofintra-snowpack processes. However, it requires minimum recalibration for application in any catchment. Simplicity and transportability are its major features but are also accompanied by low snowpack resolution. As the quantity component of a developing quantity-quality modelling scheme, this is not a critical factor.

6. Conclusions

• (1) In general the Utah energy-balance snow accumulation and melt model (UEB) has been successfully transferred to a maritime Antarctic catchment. This is a location where no snowmelt model has been specifically designed to operate. The simulation of SWE at four of the five sample sites illustrates useful application to Paternoster Valley, Signy Island.

• (2) A geographic information system (GIS) aided catchment subdivision and the selection of field-sampling sites. This resulted in eight “homogenous”, spatially non-contiguous terrain classes.

• (3) More specifically, model simulations driven by measured incoming solar radiation were generally better than those using temperature-index estimates. Poor performance at one site highlights inadequate parameterization of longwave radiation using temperature-index methods. This is an important energy-balance component in the maritime Antarctic, If full meteorological inputs are not available, the model uses “hybrid” energy-balance/temperature-index calculations for the surface-energy balance. Problems may also exist in characterizing sensible-heat fluxes.

• (4) The model is sensitive to values of snow-surface thermal conductance and initial snowpack-energy content. These physical variables should be measured in the field. In their absence, fitting of observed and simulated SWE data provide a means of assigning values. However, this method gives no indication of overall model performance.

We have demonstrated that UEB is capable of transfer to, and SWE simulation in, a maritime Antarctic catchment. Future comparisons of observed and simulated catchment melt rates will give a better assessment of model performance.