Published online by Cambridge University Press: 29 August 2014
The question of large claims in insurance is, evidently, a very important one, chiefly if we consider it in relation with reinsurance. To a statistician it seems that it can be approached, essentially, in two different ways.
The first one can be the study of overpassing of a large bound, considered to be a critical one. If N(t) is the Poisson process of events (claims) of intensity v, each claim having amounts Yi, independent and identically distributed with distribution function F(x), the compound Poisson process
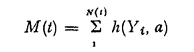
where a denotes the critical level, can describe the behaviour of some problems connected with the overpassing of the critical level. For instance, if h(Y, a) = H(Y − a), where H(x) denotes the Heavside jump function (H(x) = o if x < o, H(x) = 1 if x ≥ o), M(t) is then the number of claims overpassing a; if h(Y, a) = Y H(Y − a), M(t) denotes the total amount of claims exceeding the critical level; if h(Y, a) = (Y − a) H(Y − a), M(t) denotes the total claims reinsured for some reinsurance policy, etc.
Taking the year as unit of time, the random variables M(1), M(2) − M(1), … are evidently independent and identically distributed; its distribution function is easy to obtain through the computation of the characteristic function of M(1). For details see Parzen (1964) and the papers on The ASTIN Bulletin on compound processes; for the use of distribution functions F(x), it seems that the ones developed recently by Pickands III (1975) can be useful, as they are, in some way, pre-asymptotic forms associated with tails, leading easily to the asymptotic distributions of extremes.