The Chairman (Mr P. Fulcher, F.I.A.): This is a sessional meeting of the Institute and Faculty of Actuaries (IFoA) to discuss the interim report of the Equity Release Working Party. I would stress that the report, which was posted on the website on Friday, is an interim report. It is still going through the peer review process, but given the topicality of this subject matter we were keen to expose it to a sessional meeting at a relatively early stage.
Raj Saundh is EY’s head of actuarial in the south-west of Wales. He has worked with ERM and various associated solutions across his career with both HSBC and EY since 2007.
So why is equity release important? Well, first and foremost, equity release is a socially important product that enables asset-rich, cash-poor retirees to use their housing wealth to supplement their retirement income. There is a lot of it, about £1.8tn of £2.6tn of homeowner equity is owned by the over 55s in the UK, so there is a lot of housing wealth available.
Tom Kenny is the chair of the working party. He is also the chair of the Life Research Committee, a member of the Life Board, and of the Research and Thought Leadership Board. He co-authored a sessional paper in 2016 on: “The future of social care, who pays?” His day job is director of actuarial underwriting at Just and given the retirement lending business there, is therefore very heavily involved in the equity release space.
Charles Golding is the deputy chair of the working party. He is managing director of Golding Smith & Partners, a consultancy he founded in 2002, and he has been advising clients in the equity release market for the last 15 years.
Alex Mockridge is capital management actuary at Legal & General Retirement. He has worked on ERM since 2013, all the way from pricing to assumption setting, restructuring and valuation.
Lastly, Scott Robertson. He is the head of the financial management group at Phoenix, one of the UK’s largest consolidators. His particular responsibility is the group’s investment strategy for shareholder business and direct sourcing of assets. His team have sourced £2 billion of private assets over the last 24 months, ranging from local authority loans to ERMs.
Mr T. P. J. Kenny, F.I.A.: I will give you the background to the paper. I will talk about why equity release is important and the regulatory background to this paper.
Charles (Golding) is going to talk about the no-negative equity guarantee (NNEG). He is going to talk about existing findings on academic research in relation to equity release and explain how firms currently model the NNEG, what are the issues and touch on possible solutions.
Alex (Mockridge) is going to talk about the valuation of ERM section of the paper, drawing out the key points from the paper.
Raj (Saundh) is going to talk about structuring and securitisation of ERM.
Then, Scott (Robertson) is going to talk about their credit rating.
The working party has about 12–13 members from across the insurance sector representing investors in ERM, consultants to their clients that are investing in ERM, a whole range. So we have broad representation, as Paul (Fulcher) suggested before. We were set up towards the end of 2016. The working party has been predominantly working on the draft of this paper, but at the same time it has been a very busy period responding to consultations from the Prudential Regulation Authority (PRA).
We have also helped to set up the independent academic research that the IFoA and the Association of British Insurers (ABI) have commissioned, and is currently underway. There is an independent review group that is project managing that with the Actuarial Research Centre (ARC).
There are plenty of examples where equity release is making a real difference to people’s lives and I could have drawn examples from other providers in the market. Legal & General is one of them, obviously.
You are probably thinking there must be more to equity release than the customer side of things, and you are right. Clearly, ERMs are an attractive illiquid asset to investors. There is approximately £4bn forecast to be invested in equity release in 2018, earning an average gross yield of 5.2% with a duration, typically, in the range of 15–20 years and it is estimated by the PRA that the additional matching adjustment (MA) above corporate bonds is 75 basis points, as at the end of December 2016. So you can see why ERMs are a popular investment, particularly for annuity providers.
So who are the investors in equity release? There are only six retail annuity providers. They are writing premiums of about £4bn in 2018. Then there are eight bulk annuity providers who are estimated to complete about £35bn in 2018. There are also reinsurers, pension funds and fund managers investing in equity release and the list of investors in the UK is growing all the time.
Turning to the regulatory context to the paper. Earlier this year, David Rule from the Bank of England gave a speech entitled: “An annuity is a very serious business.” Some of the key points he made were that the Bank of England’s priority was to ensure that insurers capture the compensation for the risks they are exposed to in the fundamental spread so that the MA is not overstated and insurers hold appropriate capital against these risks. This would appear to summarise the essence of what the PRA was aiming to achieve through the regulatory changes they were consulting on in CP13/18 and has been confirmed in PS31/18.
These aims do not, on the face of it, appear to be unreasonable, but the key question that the ERM working party is trying to answer through its research and independent academic research is to establish what is the correct way to calculate the cost of the risk embedded within ERM.
There is also a debate within the profession about whether or not the approach proposed by the PRA is too prudent.
SS3/17 is a supervisory statement published in July 2017 and now updated and introduced many of the points clarified in CP13/18. Within SS3/17, and subsequently in CP13/18, there is the concept of an effective value test which is used by the PRA to determine if the MA benefit claimed by a firm is too high. The effective value test (EVT) has four key principles, which when considered in isolation seem perfectly reasonable. The four principles are: there is no reduction in risk if the securitised notes are held by the same entity; the economic value of the ERM must be less than the present value of the deferred possession of the property acting as security for the mortgage; the present value of deferred possession is the price that would be paid and settled today to take ownership of an asset in the future so the value must be less than the value of immediate possession; and the compensation for risks retained must be greater than the best estimate cost of the NNEG. The PRA argues that this is consistent with the fundamental spread allowing for the expected cost of defaults as well as the cost of downgrades a rational investor would require above and beyond the average outcome based on their best estimates and assumptions.
It is important to note that the economic value as referenced in the second principle refers to the bars in Figure 1 where the PRA expect the asset value of restructured ERM plus the MA benefits to be less than the economic value, and that the economic value is calculated in a way that is consistent with the principles already stated.
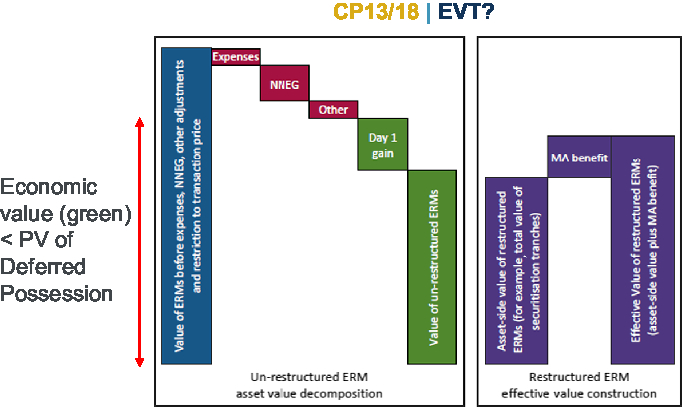
Figure 1. CP13/18 Effective Value Test?
Mr C. B. Golding, F.I.A.: Tom (Kenny) has given you an overview of the market both from a customer and an investor perspective, and he has also given you some insight into some of the PRA’s recent statements. I am going to look at the NNEG, which is one of the key features of ERM.
I am going to start with where we are currently. Most firms currently model the NNEG using Black–Scholes, using a closed-form solution. Black–Scholes, of course, has an underlying assumption of Geometric Brownian Motion, effectively a random walk with drift and that is one of the key features of Black–Scholes and one of the issues, possibly, in terms of the modelling of the NNEG. Effectively, firms model it as a put option and then model the decrements deterministically. So, effectively, you have a sum of all these put options multiplied by a probability of death or moving to long-term care or redemption.
Some firms, and it is a minority, use stochastic models for their valuation. Quite a few firms use stochastic models for validation of the Black–Scholes, so it is not necessarily fair to say Black–Scholes is the only thing they do to test whether the Black–Scholes numbers look reasonable in terms of stochastic models. Stochastic models do have advantages, which I will come onto.
Now, academic research, and we reviewed quite a lot of literature showing various features of the housing market and those features do not necessarily fit with Geometric Brownian Motion. They show that house prices exhibit autocorrelation or serial correlation. So, effectively, if you look at different time periods, you can look at a lag and you will find there is a correlation between house prices over different time periods. Serial correlation is something you often see in markets where there is seasonality, but here it is more to do with the second point: momentum effects. Effectively, if the market is going up, house prices tend to go up, and if the market is going down, they tend to go down as well. These are momentum effects.
The market also shows mean reversion so that, if you are looking at average house price inflation (HPI), you find that it moves around a long-term average and that might be a real long-term average, if you like, adjusted for constant prices rather than necessarily a nominal average.
The market also shows something that is a bit of a tongue-twister, conditional heteroscedasticity, and that basically is stochastic volatility. Volatility is not constant, unlike the assumption made in Black–Scholes. Volatility also varies by different types of property groups so you might have regional house price variations or types of properties (e.g. differences between terraced houses, semi-detached houses and detached houses). One of the more interesting features of the market is a bit like the equity market, if you like, in that it does not necessarily follow a random walk. Sometimes there are discontinuities: there can be jumps. So if you look at the 2007/2008 financial crisis, the market plummeted quite rapidly.
Figures 2–6 show annual HPI in various ways: nominal (Figure 2); real (Figure 3); moving average real (Figure 4); and by property type (Figure 6). There is a table of volatility and autocorrelation by region in Figure 5. In Figure 4, the top red line is London and London has clearly over long periods of time performed a lot better than other parts of the country. The green line at the bottom which started going up at the end was Northern Ireland. Recently, it has been doing better.
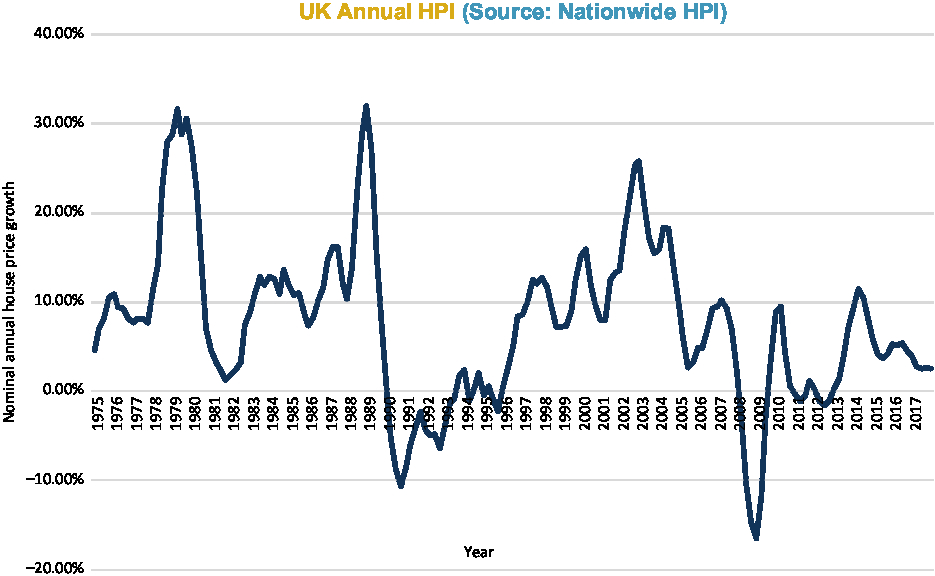
Figure 2. UK annual HPI (nom).
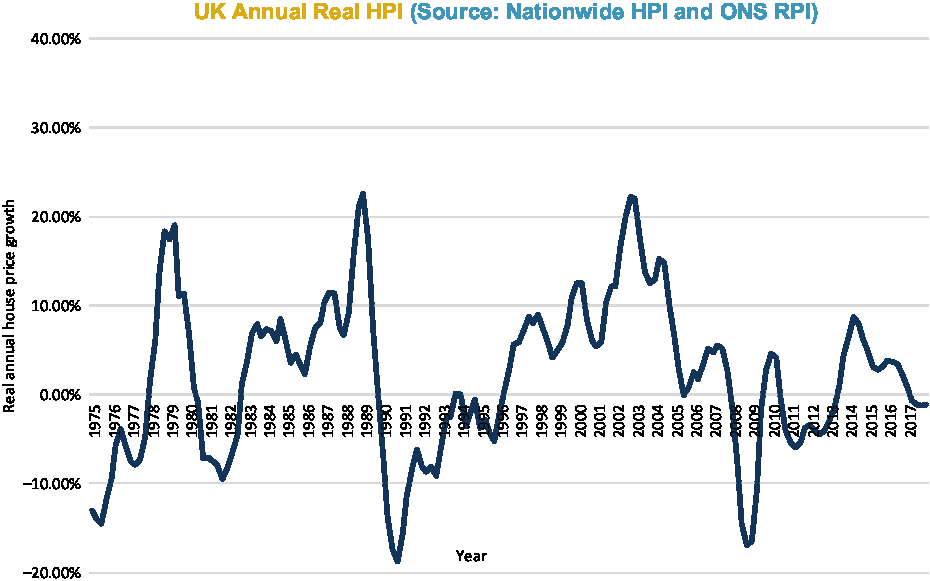
Figure 3. UK annual real HPI.
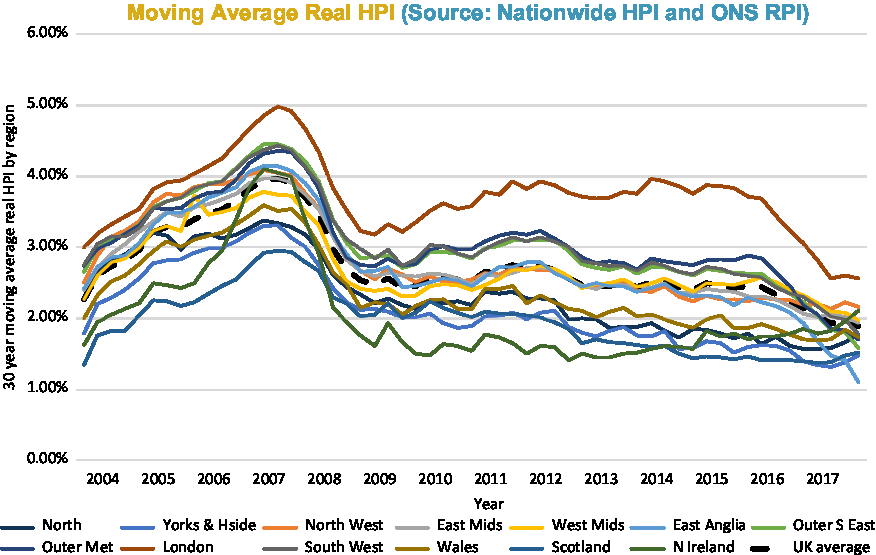
Figure 4. Moving average real HPI (by region).
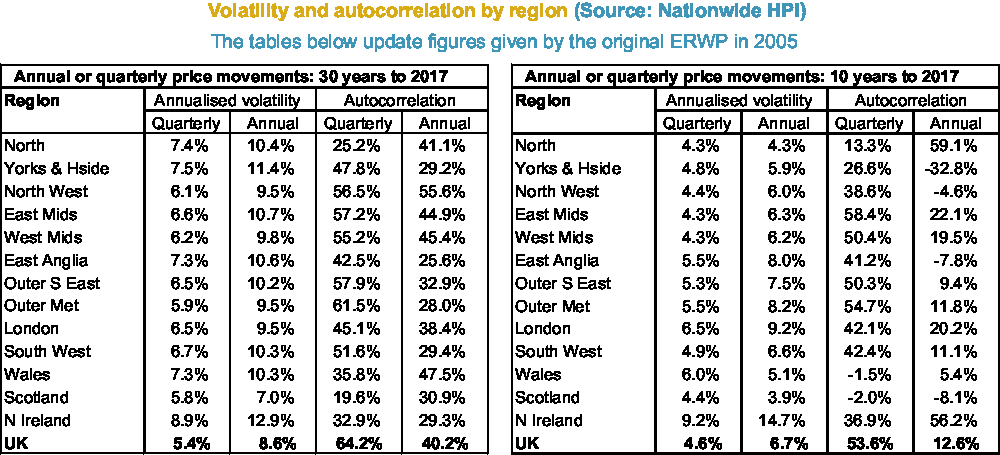
Figure 5. Volatility and autocorrelation by region.
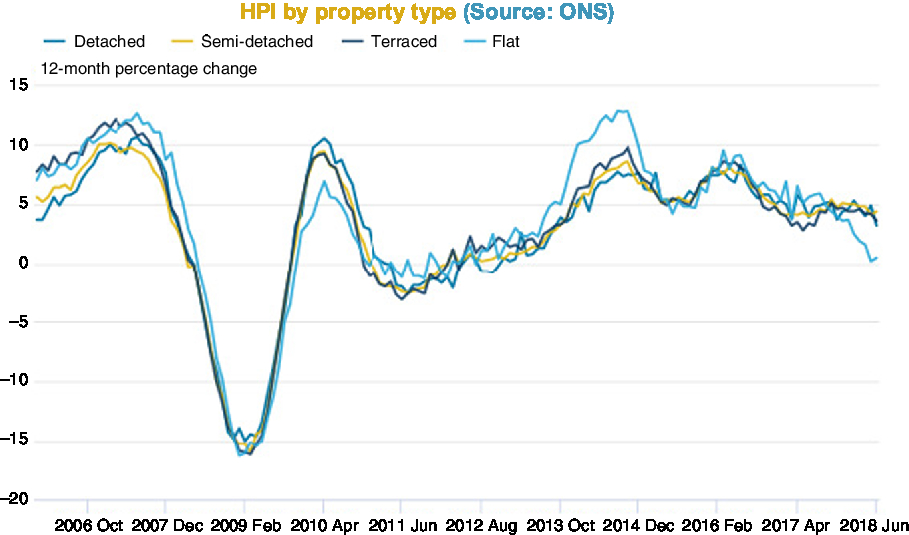
Figure 6. HPI by property type.
There are also some interesting features if you look at the 10 years since the credit crisis, probably too short to calibrate your model, but it is interesting that the volatility appears to have gone down, so has autocorrelation (Figure 5).
Looking at a one-period lag, the annual correlation seems to have reduced and there is not much correlation between 1 year and the next, although there is more correlation between one-quarter and the next.
So what are the issues? The issues clearly are whether you should be using a stochastic simulation, Monte Carlo approaches or whether you should be using closed-form solutions. The market at the moment tends to use closed-form solutions, but we did a poll at the Life Conference and everybody voted for stochastic simulation, for Monte Carlo methods, to allow for correlations between different factors.
There are issues about how you calibrate and estimate your parameters in a model and there are lots of different ways of doing it. If you are using Black–Scholes at the moment, where you make an adjustment for autocorrelation, you change your volatility rate to allow for an autocorrelation rate using de-smoothing. If you are using other types of models, you do not necessarily need to use de-smoothing because actually they are intrinsic to the model. So there are issues about calibration and estimation parameters, and they may be different for different types of models. There are lots of methods that the academics use to calibrate their models such as maximum likelihood, method of moments and generalised methods of movements.
There is the issue about real world or risk neutral or whether you could have some sort of halfway house. Clearly, if you are trying to model cash flows and you are looking at your annuity liabilities then real world seems quite reasonable. Risk neutral per se seems reasonable because that is what investment bankers use and it is a way of pricing options. The difficulty is because there is no real market in terms of what you are trying to assess. There is also the possibility of a halfway house solution, and maybe that is where the academic research is heading, but you could allow for, say, mean reversion or autocorrelation in your modelling.
There is also the issue about the deferment rate or rental yield assumption. The PRA opined on different things in this area, for example, looking at freehold and leasehold differentials, looking at rental yields and how those rental yields would have to be adjusted for costs of renting. So there are lots of issues about deferment rents or rental yields and how you calibrate them.
I do not think there is any one particular answer although the PRA have a number.
The choice of discount rate, on a risk-neutral basis, is clearly a risk-free type assumption: a swap rate if you are looking at what we currently do. But if you are evaluating it more generally, you could use a stochastic model for interest rates.
There is also the overall consistency of the valuation of the NNEG with the overall valuation of the equity release asset. So, there are lots of issues.
We have looked at what the literature had in terms of possible solutions. The most favoured were AR(I)MA, (E)GARCH, and so on. They also go from, effectively, a real-world predictive distribution to a mathematical way of converting it into a risk-free and arbitrage-free type of no-arbitrage solution. There are some quite interesting ideas out there in academic papers.
I mentioned two ways that you could do risk neutralisation. There are also issues if you want to use a closed form because the closed form clearly has an advantage if you are the regulator. If everyone uses a closed-form solution that looks very similar, then it is easy to see whether one firm is stronger than another. But a more complicated type of modelling requires compromise and suitable calibration. Even what we do at the moment, Black–Scholes, is a compromise in that we up the volatility rate to allow for autocorrelation.
Having looked at all this academic literature, we decided we did not really know what the solution was. There are lots of possible solutions out there and we did not come to a conclusion. So we realised we needed some independent academic research. The IFoA, in conjunction with the ABI, has commissioned research, and this research is under the oversight of the ARC. The research is being carried out by the Kent Business School. Professor Radu Turanu is leading the research.
There is a joint ABI–IFoA review group with Professor Johnny Li as the chair. Johnny has written a number of papers on the equity release market as has Professor Radu Turanu. Radu has been mentioned in some of the PRA papers. The review group is split 50/50 between the ABI and the IFoA. We have already had some interim results and we are expecting a second set of interim results. The first set has been shared with stakeholders within the IFoA and ABI, and we are hoping to have published results sometime early next year – the final results. A lot of work has already been done, but there is still a lot more work to be done.
Mr A. Mockridge, F.I.A.: I am going to talk about some general topics in ERM valuation that we covered in our paper. I think it is fair to say the methodology for valuing ERM has been in a lot of focus in recent years and it was the original Hosty et al. (Reference Hosty, Groves, Murray and Shah2007) paper that laid the framework for where we are today. In our paper, we aim to provide a guide to current market practice and we also aim to stimulate a bit of debate on some topics, such as International Financial Reporting Standard 17 (IFRS 17) and Solvency II.
The key question on IFRS 17 is whether an ERM is an insurance contract. Our research and conversations with practitioners indicate that the current market practice is to treat ERM as investment contracts. However, the wording of IFRS 17 – “a contract is an insurance contract only if it transfers significant insurance risk” – means that it can be argued that a NNEG is an insurance feature. If that was the case and ERM were to be in scope of IFRS 17, then this would be a significant departure from the current market practice.
Although we have not gone as far as to explore how you would value, theoretically, an ERM under IFRS 17, we anticipate that it would involve grouping contracts and setting up things like contractual service margins and risk adjustments. This issue has been picked up by the International Accounting Standards Board (IASB) and it was one of 25 issues in their recent staff paper “IFRS 17, Concerns and Implementation Challenges.”
Under Solvency II, there has been a history of regulation, starting pretty much from the beginning of Solvency II itself. I think it is fair to say there has been a continued regulatory focus, especially around points on the MA and, as Tom (Kenny) was mentioning earlier, the four principles of SS3/17 have now been consolidated into the effective value test in PS31/18.
We built a simplified model to run the effective value test and I have two examples here (Figure 7).
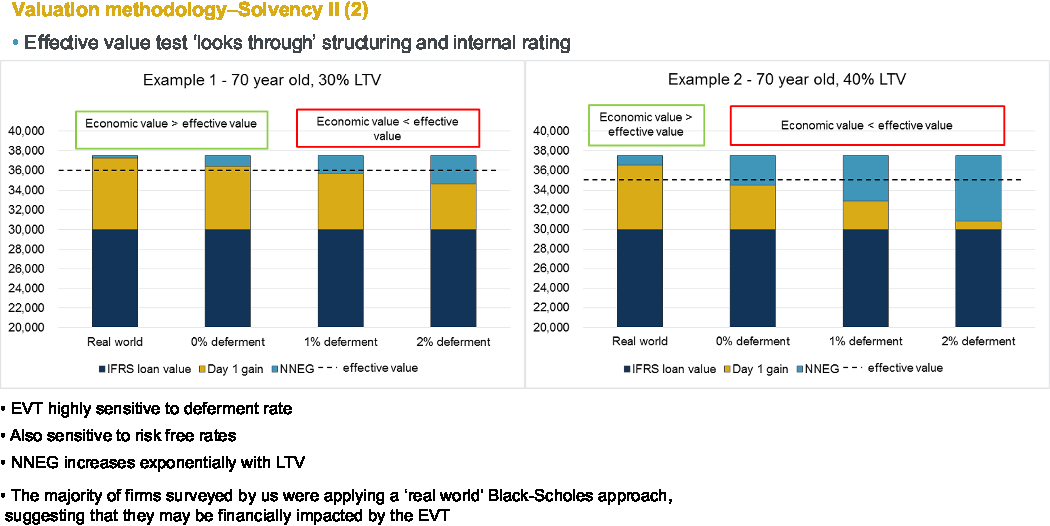
Figure 7. Valuation methodology – Solvency II (2).
Example one on the left is a typical 70-year-old customer with 30% Loan to Value (LTV), and example two on the right is an identical customer with 40% LTV. The dotted line represents the notional effective value and if the real NNEG is too high, then the effective value test fails and the company would not be able to claim that level of MA.
So, we can see clearly that the current market practice of using a real-world technique to value NNEG places a much lower value than using the risk-neutral approach set out in the recent PRA guidance and that is true even for a 0% deferment rate, which the PRA said is the minimum possible deferment rate to use. It is interesting to see that for the higher end of the LTV market the amount of MA claimable, or the maximum amount claimable, is quite significantly lower than something more in the medium LTV range.
Finally, there were a couple of topics that we would probably have liked to include in the paper, but came just too recently off the press. PS31/18 has really solidified the effective value test from CP13/18 and it is also signposting to further consultation activity early next year. And the IASB has proposed delaying IFRS 17 implementation by 1 year and, potentially, this could give the industry more time to engage on ERM and whether or not they could be de-scoped.
Mr R. S. Saundh, F.I.A.: So, structuring, where has it come from and why securitise? If we look to a few years ago, there were very few securitisations in the market. I think everyone is well aware that Solvency II regulations changed the landscape for ERM providers and the requirement to have fixed cash flows in MA portfolios meant that a solution was needed.
Securitisation is one of the range of options that is available and from the survey that we conducted with various market participants, and to the working party’s knowledge at the minute, it is the only solution that is actively out there and being used by annuity providers in the UK.
So what do they look like? In a nutshell, insurers write the ERM within their insurance company. They are passed into a securitisation structure, a special purpose vehicle. That structure issues some notes. We are going to call them senior or rated notes. These are bought by the company’s MA portfolio. There is also a junior layer, which is typically unrated, which may or may not be held by that firm. There is one example where that has been bought by another company outside of that insurer.
So we have portfolios of ERM and have had them in the market for a long time and there is a lot of discussion around securitisation. Why is there so much discussion?
Figure 8 sets out a few of the additional risk implications of having securitisation. The dark blue line represents a series of cash flows from a portfolio of ERM. The gold line is a securitised note, and the two dotted lines represent two different scenarios which present the potential variability in the cash flows. This tells us two things. The first is in the scenario where my portfolio is providing less money than my rated note, which I put in the MA portfolio. I need liquidity and I need money, to be able to find money from somewhere outside my portfolio of mortgages to meet that fixed cash flow requirement. The second is shortfalls. There I have to save up money now to meet future needs or find money in the event where I am falling short in the future. The green line is where I have surpluses emerging in the future.
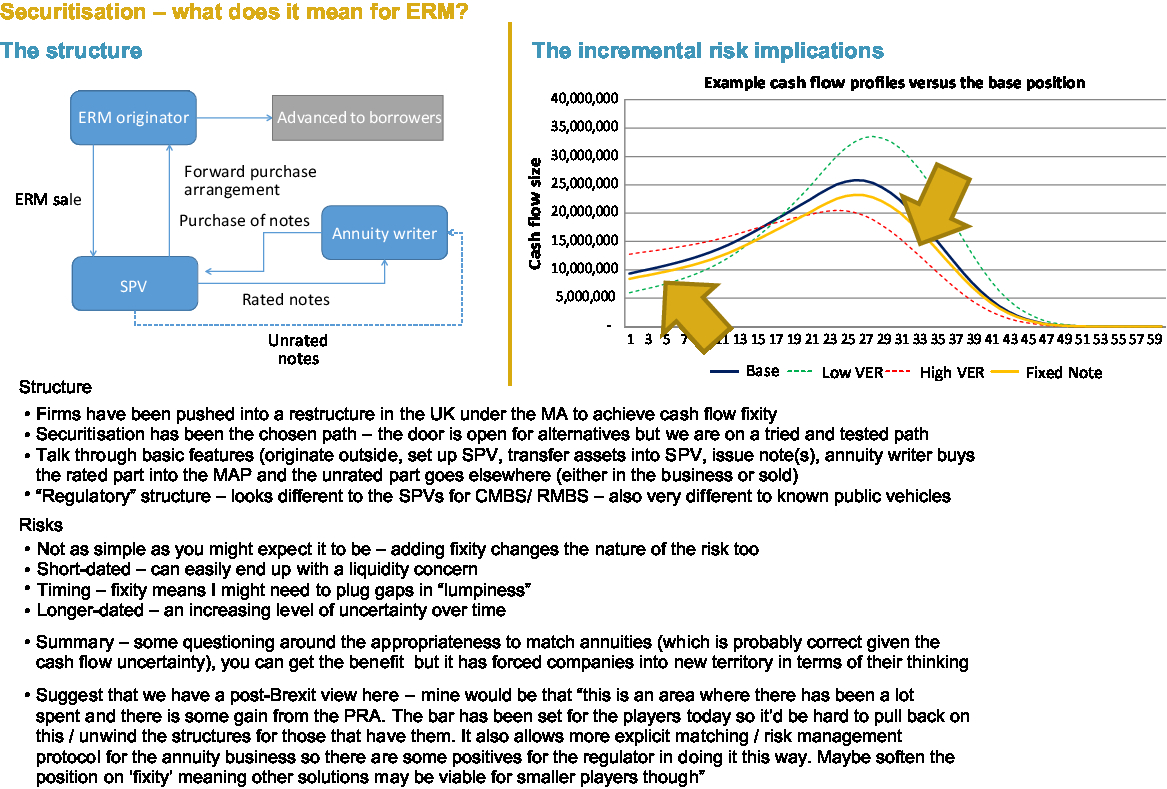
Figure 8. Securitisation – what does it mean for ERM?
So, different risks. What issues do firms have to balance against one another? Yes, securitisation has a series of notes. Yes, they may be of different sizes, and I have talked about liquidity and potential cash traps as well. Most firms are writing new business. Therefore, I want, and need, a vehicle that is flexible or that in some way allows me to get the benefit from writing new assets into my annuity portfolio in as slick a way as possible.
So, where is the market today? I think the answer in every single one of those example dimensions is in a quite different place. I think that reflects the need for different firms to look to optimise different things. Some look at financials, some look at complexity. Cost is also really important because it is clear that it is not cheap to achieve compliance.
So, the message here is that there is no one-size-fits-all solution in the market. I think the other message that we took away from our survey is that this is a regulatory construct and not a market-based construct, which mean very different things. There are advantages to keeping life simple for yourself, if you can. Alex (Mockridge) touched on valuation and that is the final piece that I will touch on.
So, there are valuation methodologies in place for underlying portfolios, but now I have separated those portfolios into a series of notes and issued them to potentially two different places. So where have firms reached with that valuation?
Well, first is the principle of retention of value. I have a portfolio of ERM. I structure them. I issue some notes from that portfolio of ERM and you would hope that what I issue is equal to the sum of its parts. There are learnings to be taken here for I will have some rated notes from that securitisation. There is a junior note from that securitisation as well and there are issuances in the market. I guess the question really is: which one do I value first?
If I look at the rated notes, we see firms within our survey who look at valuing that first, look at equivalent assets that might look and feel like that rated note. If we look at the junior note, then perhaps look at something that is more equity like. I think the one consensus we did obtain was whilst there were different starting methodologies, most firms then use an alternative approach to test whether the answer that they produced is reasonable or not.
Valuation in stress on the asset side is typically a mechanical application of the valuation in base, so I will not touch on that any further. The valuation in stress on the liability side – we have talked about the MA in the policy statement issued in the update of SS3/17. In principle, and I have quoted the SS8/18 there, firms cannot just consider a mechanistic application, which is of the matched adjustment in stress. A mechanistic application in this sense is to revalue the underlying portfolio, revalue the notes and then re-rate the notes from that securitisation and apply my fundamental spread parameters to that calculation. Now, over and above that, there is a requirement in that same supervisory statement to consider the fundamental spread and stress. Within the working party that will be something we will consider further and will be an area of further research. What I will just dwell on though is that what it does is place a lot of onus on rating. It is the quality of the rating and the ability to re-rate the issuances on a frequent basis within capital models that is important.
Mr S. A. Robertson, F.F.A.: I am going to look at the approach to assigning internal credit ratings to restructured ERM. I am going to begin by looking at the need for such a rating and then I am going to consider the approaches actuaries might wish to take to determine an internal credit rating.
So first of all the rationale; it is a regulatory requirement in Solvency II. Solvency II requires insurers to assign internal ratings to their senior notes of our ERM restructure for the following reasons. Number one: the internal rating is required for any large or complex exposure. Even if you have an external rating, you still need to do an internal rating. Now restructured ERMs are likely to be both a large and complex exposure. Typically, the securitisations are large as they are in the hundreds of millions, and also likely to fit into the category of being complex because, as Raj (Saundh) has just talked about, we need to tranche the underlying cash flows of ERM. We have to apply waterfall payment structures and we may have to add other structural features like liquidity facilities and contingent reserves in order to satisfy the eligibility criteria.
Second, in order to apply the MA to our senior notes, which is the whole reason we are doing it, we need to map the internal rating to a credit quality step in order to select the appropriate fundamental spread from the published by EIOPA in the Solvency II delegated acts.
Finally, the internal rating process can provide evidence to support compliance with the Solvency II prudent person principle. These principles require the insurer to demonstrate that it can properly identify, measure, monitor, manage, control and report the asset risks to which the firm is exposed.
So, the requirement for an internal rating is clear from a regulatory requirement. I believe in the prudent person principle, as insurance companies handling other people’s money should know what they are doing and be able to meet those principles.
What is less clear is how an insurer should go about assigning such an internal rating. In the PRA’s supervisory statement of SS3/17, it stated that: “The internal rating should lie within a plausible range that could have resulted given by an external rating agency” or, as we have come to know them, External Credit Assessment Institutions (ECAI). The supervisory statement went on to say that: “The internal ratings should be broadly consistent with the ECAI approach.” So, given these regulatory requirements, in the next section I am going to look at how insurers can demonstrate this broad consistency. In preparing the paper, we have spoken to ECAIs, namely Fitch and Moody’s, to look at how they rate notes issued by ERM securitisations.
Our initial discussions led quickly to the following conclusion. There is no single defined approach to rating ERM notes. But wider than that, there is no defined approach to rating any debt instrument, which was a bit disappointing. The ECAIs apply different methodologies, assumptions and expert judgement in determining rating decisions, and as a result, this can lead to a different ECAI rating for the same exposure. This is a common occurrence with corporate debt. You can have one ECAI that will rate your debt single-A. You will have another ECAI that will rate exactly the same debt triple-B. Therefore, we came to the conclusion that consistency does not mean exactly the same approach or rating as an ECAI. If we are clear on what consistency does not mean, can we be as prescriptive on what a consistent internal approach should look like?
We can make the following observations. First, the analysis should model the asset cash flows of the underlying ERM portfolio, under a range of individual and combined stress scenarios. That is a consistent approach. The analysis should also consider non-market risks. Those include due diligence of the legal risks, operational risks and regulatory and compliance conduct risks to which you are exposed. On the other side of securitisation, you need to be able to analyse the resilience of the structure of the senior notes that you have produced to meet those debt obligations. Finally, for the rating analysis, you should apply expert judgement in determining that rating decision, taking into consideration the results of your scenarios. But also, when you are assigning the weight you are going to place on those results, you need to take into account the plausibility and the materiality of those results.
So, scenario modelling is an important part of the rating process. I now want to consider how such scenarios might be derived.
The general observations we made from discussions with ECAIs was, first of all, we have the usual letter ratings – triple-A, double-A, single-A, all the way down to single-B. Speaking to the ECAIs, it was clear that the triple-A scenario is designed to cover something they have never seen before. That prompted the question about how you determine the bounds if you have never seen it before. You must have to bound it, or else you could just assume a 100% house price fall. You could assume that all the policy holders die tomorrow, or pre-pay. So, asking the ECAIs about that, they were clear to say: “Well, we employ expert judgement to determine what those bounds are,” which comes back to my point – plausibility, or the feasibility analysis.
At the bottom end of the scale, single-B is a good proxy for what the best estimate-based scenario might be. For house price stress scenarios, we concluded that the scenarios that firms should use should be those that have been published by ECAIs. The rationale for that was that the ECAIs, for their ERM ratings, will generally rely on other products that they have already rated that are similar, have similar house price-type risk factors, like residential mortgage-backed securities (RMBS). So, there is a much greater wealth of experience the ECAIs have on house prices.
When it comes to other risk categories, like mortality, longevity and morbidity, those are more bespoke and much more related to the specific portfolio that they are rating.
The ECAIs made clear that they would seek to utilise data that the client or the insurer had, to support their rating scenarios. They were clear on one point, which was the data, and how much data is material? They did say that the data should cover at least one full economic cycle, in order to give them a breadth and depth of data to support their analysis.
The other thing the ECAIs have told us is that when they rate triple-A and double-A, they look at the timing and the amount, so you have to pay the amount you promised to pay, at the time you said you would pay it. When you go to single-A and triple-B, what they are now rating is not the timeliness of the payment, but over the full maturity of the instrument, will you get your money back? Will the debt holder be fully paid?
This was a subtle, but important, difference in how a rating agency looks at it, compared to how an insurer might look at it under the MA-type world of timeliness, as well as amount. We are trying to be consistent with an ECAI, not with Solvency II.
One of our other key conclusions is that expert judgement plays a fundamental part of an ECAI’s rating approach. Importantly for actuaries, rating decisions are not purely a statistical exercise. The computer will not give you the answer, because if it does, you are not being consistent with an ECAI. The scenarios will inform your decision, but it is not the end of the process.
I would stress that, if you spend as much time considering the result as you do doing your modelling, then that will give you in a much more consistent approach with the way an ECAI would look at rating an ERM, or for that matter, any other debt instrument. As I said at the beginning, consistency does not mean the same.
The Chairman: We will now open to questions from the floor.
Mrs J. K. Hicks: I did my dissertation on whether house prices in the UK have a unit root. So, for those that do not remember from CT6, that is whether they have a random walk, if you take the first difference, if it is an AR1. And that is what I found, that it was an AR1. It was not entirely conclusive, but it was fairly clear.
Also, my diagrams look slightly different from yours. I used Nationwide quarterly house prices. I saw you used Nationwide. There is quite a lot of research on regional differences, and I did not look into that. However, the academic research I looked into on the UK in general, a couple of sources just stated that the house prices do have one unit root, so that was almost taken for granted. It is interesting to see slightly different results, and I would be interested to ask later, or see in the report, what was different in your methodology?
Mr Golding: I think it was not really our methodology. It was the methodology in various academic and professional papers, and so we were looking at that. If you like, that is what we have reported. The papers primarily covered the UK, but some were on overseas markets, so there are lots of interesting things in there. So, it is academic research, not our research, and we decided, having looked at it, that we needed some academics to help us out.
Mr S. Lazzari, F.I.A.: In the survey of academic research that you looked at, did you find any research that agreed with the apparent view of 50% of the people in this room, that using a very basic risk-neutral valuation approach with something like a normal distribution underlying it, is prudent?
Mr Golding: I do not think we really found that. I think there are some papers that suggested Black–Scholes might be an appropriate methodology, but most papers go for much more complicated models, and not necessarily closed-form solutions. If you were a regulator, you might prefer closed-form solutions.
Everyone is saying they want Monte Carlo modelling, stochastic modelling. As a regulator, you might like something to benchmark people by, and with stochastic methods everyone will do their own thing and it would be very difficult to compare one firm against another. So, I can see benefits of closed-form solutions, which the audience does not necessarily see.
Mr Lazzari: Yes. I note in the paper you say that we should take a step back and think about adding in all these extra features that you can with stochastic models.
Mr Golding: Yes, but then also look at whether we can actually still use Black–Scholes with suitable calibration. So, we want to look at the ideal, and then say, from a practical point of view, is there something else that we really need? Can we still use Black–Scholes, and if so, how do you actually calibrate it? We make adjustments for autocorrelation at the moment. We de-smooth. House prices are actual real sold house prices in the Nationwide index, they are not like commercial properties. There is a lot of correlation from one peer to the next. People, when they decide on their house price, get their estate agent to tell them the price based on representative properties.
I do not want to pre-empt the academic research, because I have seen the interim paper, but effectively, we are looking at the best fit in terms of models. Geometric Brownian Motion rather than Black–Scholes does not necessarily give the best fit if you are trying to project forward, or even back test. So, other models are better, but can you still use something else?
Mr Lazzari: The point I am making is that I would imagine that any more refined, sophisticated model, based on risk-neutral principles, is going to increase the value of these options. My concern is that such approaches are going to have limited uptake given the results of the survey that has been conducted of the people in this room.
Mr Golding: I do not necessarily think that is the case. If you look at Black–Scholes, it assumes constant volatility, and volatility over a long period will be based on the square root of time. If there is mean reversion, the volatility, using a constant volatility, could under or overestimate, depending on the time period. So, I think you have got to be careful about thinking that Black–Scholes gives you the correct answer, because it might give you an answer in the mid-point. But you could be either be under or overvaluing, using Black–Scholes. The whole point is we are trying to get something that fits house prices better.
Mr M. W. Barnard, F.I.A.: Just a couple of thoughts. I think the policy statement talked about reviewing deferment rates, and looking at these relative to real yields. It is something I have been thinking about a bit, because that gap, R minus D, is something that does appear in the Black–Scholes model. That is in CP13/18. Just thinking about this in a real-world analogy, you know, if you were looking at an equity that had a very high yield, you would probably expect no dividend growth from it, and you would maybe expect not to have much left of it after a few years, whereas if you looked at a stock which had a very, very low dividend yield, you would be buying it on the anticipation of growth. I think that is relevant in thinking about the NNEG, that if you are buying dilapidated, old properties with high yields, then you are going to expect to lose money on them. If you are buying something with a very low yield with expected growth, you should expect to make money. I am interested if you had thoughts on that.
Mr Golding: If you look at the data, some of what you say may be true, but not necessarily as much as you think. So, if you are looking at some regions, some rental yields might be quite high. The growth necessary has not been impaired that much. That is one of the issues for the academic research, if you like. I am not going to give an answer to that one, but it is not necessarily clear.
Mr Z. Galyo: The rating agencies generally have a timely payment of interest, and automate payment of principal in the structured finance world. By doing this, the triple-A and double-A, is the most senior-rated tranche. So, that is why they go for a timely and soft payment of interest, but their pass-through rating is always ultimate payment of principal. They are extremely uncomfortable to move away from that ultimate payment of principal concept, because we are asking them, basically, to rate liquidity, and that is just uncomfortable for them. So, when it comes to our conversation with the agencies, to try to get them into this timely payment of principal conversation, they go into judgement credit committee panels, where they actually discuss, “How did we calibrate, properly, the stresses around timing of cash flows which are prepayment, and recovery speed?” Everything that is not really credit in the past few contexts.
Our experience is that they are becoming extremely conservative. At that point in time, the rating exercise typically falls over because it comes to a very difficult rating that does not make economic sense anymore. So, I am a bit worried that if, suddenly, there are all these experts in-house across the insurers, what is a level playing field, and who will be judging the right level of calibration, if the agencies themselves are uncomfortable?
My second point is when you mentioned that on the junior note there is a deferral allowed. Again, in the context of a mezzanine (or junior) note, that is their normal practice.
You said that we comply with rating agencies, rather than MA requirements. Does it mean that you would be happy to put that bond into your annuity portfolio and allowing an extension of the notes, rather than a default, which I think is technically a requirement under the MA?
Mr Robertson: Yes. I think there could be consistency with corporate bonds, because the single-A or triple-B corporate bond is in the MA portfolio. What these guys are saying is that when we look at that rating, it is the timeliness of the payment that is important, but it is not fundamental to obtaining that rating. It is about being paid.
I think insurers should take that into account, in terms of their internal rating, if they are comfortable with that risk. It applies to rating more generally, not just ERM. Rating is across all of the instruments.
I think, on the triple-A, what we found is there is a wide dispersion of views about what is a triple-A scenario. Rating is an opinion, not a fact. As Raj (Saundh) was saying, we have some securitised notes that are rated highly.
I think it is difficult for one insurance company to look at another insurance company and say, you know, “We are different. You are double-A, we are triple-A. Oh, that means you must be wrong.”
As shown by the split ratings you find in a normal corporate bond, for example, single-A or triple-B, a one letter difference is not unusual. I think what we were looking to see is whether there can be a consistent approach, not just with ERM, but an approach which can be applied to all assets?
Just in principle, across any insurance company’s portfolio, whether it be a MA portfolio or a non-MA portfolio, that approach can be different. So, your experiences might be different from my experiences, or somebody else on the panel’s experiences. What we are saying is being different is not wrong.
The danger we have is from a regulation that says, “If you differ from me then you are somehow wrong,” means that there would be a herd mentality, and that is what I am concerned about.
Mr Galyo: I agree that this is a rating opinion. They are regulated anyway, and they cannot state otherwise. The point is, though, all insurers would be motivated to be the most aggressive on the rating, because that will have an economic impact in driving the market. So who will make sure that there is a level playing field, because whoever takes the most aggressive view will potentially be the most successful in the business?
Question from a member of the audience: Obviously, there has been a lot of debate about what sort of modelling approaches you should use. Have there been any studies that give some order of materiality in terms of model risk and basis risk? Are the panels seeing some convergence, in terms of market practitioners and the regulators coming to some consensus as to how we should really evaluate these instruments?
Mr Mockridge: Yes. I think what we saw in our survey is actually a very wide range of different market practices for valuing ERM. That goes for Solvency II, as well as IFRS. So, you can see that one of the PRA’s main concerns in implementing the effective value test was to try and achieve more consistency, especially across internal ratings and MA. I think that is why we really want this research to happen. We want to help provide some sort of thought leadership and to continue to develop actuarial knowledge on how to value a NNEG. Then gradually, since ERMs are a relatively new product type, and we do not have the same kind of history that we have with annuities and term insurance, for example, we will see more and more convergence as ERM becomes more mature as a product and as more thoughts and opinions are added to the professional debate.
Mr Saundh: I think, whilst there is limited convergence in the valuation methodology that is used, we probably have seen and observed how structuring has become an issue for firms, and there has been an element of fixity introduced to cash flows – the increased need for validation, and using, trying to use, or looking to use alternative approaches. As I mentioned, there are different risks that do crystallise and come to light, and therefore for some firms, who potentially are using a deterministic model for particular uses, whether it be for valuation or for rating, are also thinking about a stochastic model to test the overall appropriateness of that, using a range of solutions rather than a single solution, to come up with their valuation of potentially the asset, potentially the NNEG, potentially the MA or even the rating. There is no synergy at the moment, in the use of different techniques across each of those components.
Mr D. Land: I was surprised that you were arguing about the differences between option models, when you have not yet fixed the right method of calculating the forward. That seemed like a pretty major source of possible error. I do not really understand why there is much dispute about what the forward should be.
An interview question that I have asked for 20 odd years is how do you calculate the price of a house that you want to exchange the money for in a year’s time? The candidates who get the job are the ones who understand that it is the difference between the financing rate for the house and the rental yield on the house. The candidates who do not get the job are the ones who think it has something to do with what house prices are going to do over the intervening year. Yet, of the people here, half of them seem to think it is a good idea to think about what house prices are going to do over the period of the option. I wondered if somebody can help me understand that.
Mr Golding: I will make one observation. It depends what you are using the modelling for. If you are trying to model cash flows, and you have annuity liabilities, then some sort of option pricing is not necessarily what you want. You want to project forward what is going to occur from your mortgages, how they are going to be redeemed and what the sort of known negative equity cost will be. So, you have to do that on top of various scenarios, but it is more of a cash flow-type thing, it is not an option pricing thing. I am not sure that is answering what you are saying, and I can see what you are saying.
Mr Kenny: I think the debate has been around whether or not option pricing for the cash flow modelling is what you should be using. So, that is a debate that we have been having.
Mr Golding: Yes, and I think there is another thing about option pricing. Investment bankers have not typically been valuing 30-year options, which they could be on these things. So, we are trying to extend and extrapolate something investment bankers have used for shorter term options into something that is long term. Is that right?
Mr Land: I do not disagree that it is difficult to come up with an actual number, and that there is a large range of possible funding rates you could think about. So, I think the PRA thinks you can probably fund a house at LIBOR flat, which seems remarkably difficult. Some sort of estimate of long-term rental yield is also very difficult to come up with.
Mr Golding: Also, if you are looking at a Black–Scholes, and you are using a risk-free rate, and you are assuming some sort of constant rental yield, current risk-free rates may be artificially low, because of quantitative easing and things like that. So, the effect we have is that the put option is pretty much in the money. There is a question about whether that is right or wrong, so there are lots of issues, and I agree with you. I do not know the answer.
The Chairman: I think the working party probably have not had a chance to digest it in full because it came out yesterday, but there is quite a debate in the PRA paper. That included comments about the cost of funding. Is it really, as you say, risk-free? It is not even LIBOR flat. It is LIBOR minus a credit risk adjustment. Is the MA a real-world calculation? People made the analogy to corporate bonds, and if we valued the corporate bonds market consistently, we would knock off the credit default swap spread. Again, that would be a fairly obvious question to ask one of your interview candidates, but that is not the way the MA works.
Now, to be fair, the PRA, in their paper, gave quite robust push backs on those push backs. I think digesting what is in there and maybe thinking about that, and feeding that into the academic research that is being done will hopefully leave us in a better place. They are all very valid points.
Mr Golding: We have passed a copy of the PRA’s latest papers to the academics, so they are definitely going to look at those points, although they have parameters in terms of what that should cover. It does not necessarily cover everything that the PRA talks about, because that is not what we have commissioned him to do.
The Chairman: If people have not read it, the PRA paper is definitely worth a read. Not just the end outcome, but the rationale for how they got there. It does raise a lot of these issues and debate the points in a way that I think is worthy of reflection and maybe challenge, maybe acceptance. I think it is a very valuable contribution to the debate.
Mr G. J. Mehta, F.I.A.: Let us consider the issue around internal securitisation, with the PRA, or any regulator, having a problem of making sure that the approach is consistently applied. Why not solve the problem by requiring all the firms not using internal securitisation to avoid biases or repeated expert judgement application, to use external securitisation to transfer the risk in a market-driven manner. That would solve the race for obtaining a good rating on senior notes and junior notes, and thereby needing more MA.
Mr Saundh: I completely see that. Is internal securitisation the only solution that is available? No. Could firms, if there is the right solution available in the market, use that and bring the notes back into the MA portfolio? Absolutely.
At this stage in time, maybe because we are early on the journey, maybe because the solutions are not quite there yet, such solutions are not prevalent in the market today. Would that solve all of the issues? It probably comes down to firm specifics, does it not? About A, the economics and B, some of the potential issues around external securitisation and transferring these assets to someone else, in some way, shape, or form, which will give rise to its own issues as well.
The purpose of what they are trying to achieve here is not access to capital markets, as you are with other securitisation vehicles, but in achieving a regulatory construct. So, absolutely, it is not off the table. Absolutely, there is potential for there to be a viable option in what you suggest. I think we are seeing the start of the journey, which is 2 years down the line. The market is just not there yet.
Mr Robertson: It was done, because there are external securitisations of ERM, but those were done in a private market. You are buying private assets, be it ERM or anything else. You can have all the theory in the world, but it is the same as buying a house. I do not look at my LIBOR curve and work out the option price. You want it, and if you do not get it, there might not be anything else. You have to take the opportunity cost of the risk of what else you are going to invest in?
I think for external securitisation, they were originally done for people wanting much shorter investments. They wanted to give the money for 5 years, and get it back in 5 years, so it is like a usual 7-year with 5-year call, kind of, structure. That did not work very well in a crisis, because you have a mismatch between the duration of what the investor wants, and what the asset can provide.
I think, from the insurance industry perspective, we are long-term patient investors. We have long-term liabilities, and therefore, we have patience and want to invest. So, with external securitisation risk transfer, you have to find the right audience. As Raj (Saundh) said, that audience is quite small. It tends to be, well, you tend to look in the mirror, and you will see yourself.
That is why I think equity release helps people. It is a way an insurance company can look over the long term to find long-term financing. I certainly think external securitisation could catch on. I think there are quite numerous hurdles and I do not think that, just by creating an ECAI, you are just passing from one expert judgement to another expert judgement.
That will not solve the fundamental question of what you think is going to happen in the future? It will always be expert judgement, so you just outsource it to somebody else. As we said, you still have to do your own internal analysis, so I think the market is not there, but I think with any evolution, it could move on.
It would require a step change in other investors, not just insurance companies, but sovereign wealth funds, hedge funds, etc., to say to their clients, “I am going to put your money away for twenty years,” and develop that market.
The RMBS market that grew up before the crisis was not funded by people that wanted to put their money away for 20 years. They looked at it almost like a deposit account. They were looking at one, 2-year notes, and getting the money back. So, that is why that market was so successful, because it is just a vast universe of people all around the world, who said, “Oh, I will put my money in that for a couple of years,” and it is very liquid. They treated it, before the financial crisis as it were, as if it were a bank account. That is why the interest rates on those instruments dropped to virtually LIBOR flat.
Equity release is a long-term illiquid asset, because the householder will be alive for hopefully many, many years, and therefore to liquidate that asset is not an option. So, you need to seek, like any market, a market that brings investors and borrowers together. That is certainly, I believe, somewhere that can grow, but it is going to be a long road, I think. That is my personal opinion.
Mr Mockridge: Yes. I think it is quite interesting to think about that, with the new regulations published yesterday, and so on. Yes, if the general view of the 52% of people in the room is that it is more prudent than other regulation elsewhere, then it is certainly something that we could see more of in the future. Offshoring, or regulatory arbitrage, if you like, where counter-parties who are not regulated by the PRA would take on this risk from insurers, perhaps, who are. So, yes, although there do not seem to be a lot of examples of this in our research, it is certainly something that is interesting to think about for the future.
The Chairman: Thank you very much for all of your contributions. This is an interim paper, and it will be revised, so watch out for the final paper, and also hopefully, February-ish, we will have another event to present the results of the academic research that has been commissioned. I think that may well be the place to debate some of the questions that have been raised on some of the more fundamental aspects of valuing a NNEG, which is the specific focus of that research.










