Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T08:25:44.940Z Has data issue: false hasContentIssue false
  • English
  • Français

INTUITIONISTIC ANALYSIS AT THE END OF TIME

Published online by Cambridge University Press:  04 December 2017

JOAN RAND MOSCHOVAKIS
JOAN RAND MOSCHOVAKIS*
Affiliation:
DEPARTMENT OF MATHEMATICS OCCIDENTAL COLLEGE LOS ANGELES, CA90041, USAE-mail: joan.rand@gmail.comURL: http://www.math.ucla.edu/∼joan/
Get access Rights & Permissions [Opens in a new window]

Abstract

Kripke recently suggested viewing the intuitionistic continuum as an expansion in time of a definite classical continuum. We prove the classical consistency of a three-sorted intuitionistic formal system IC, simultaneously extending Kleene’s intuitionistic analysis I and a negative copy C° of the classically correct part of I, with an “end of time” axiom ET asserting that no choice sequence can be guaranteed not to be pointwise equal to a definite (classical or lawlike) sequence. “Not every sequence is pointwise equal to a definite sequence” is independent of IC. The proofs are by Crealizability interpretations based on classical ω-models 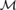${\cal M}$ = 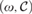$\left( {\omega ,{\cal C}} \right)$ of C°.

Keywords

03F2503F5003F55intuitionistic analysiscountable choicenegative interpretationreadabilityomega-modelclassical analysisconsistency proof
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 23 , Issue 3 , September 2017 , pp. 279 - 295
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Birkedal, L. and van Oosten, J., Relative and modified relative realizability . Annals of Pure and Applied Logic, vol. 118 (2002), pp. 115–132.CrossRefGoogle Scholar
Kleene, S. C., Introduction to Metamathematics, D. van Nostrand Company, Princeton, 1952.Google Scholar
Kleene, S. C., Formalized Recursive Functionals and Formalized Realizability, Memoirs, no. 89, American Mathematical Society, Providence, RI, 1969.CrossRefGoogle Scholar
Kleene, S. C. and Vesley, R. E., The Foundations of Intuitionistic Mathematics, Especially in Relation to Recursive Functions, North Holland, Amsterdam, 1965.Google Scholar
Lifschitz, V., Constructive assertions in an extension of classical mathematics . The Journal of Symbolic Logic, vol. 47 (1982), pp. 359–387.CrossRefGoogle Scholar
Moschovakis, J. R., Can there be no nonrecursive functions . The Journal of Symbolic Logic, vol. 36 (1971), pp. 309–315.CrossRefGoogle Scholar
Troelstra, A. S., Choice Sequences: A Chapter of Intuitionistic Mathematics, Oxford Logic Guides, Clarendon Press, Oxford, 1977.Google Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction, vol. I and II, North-Holland, Amsterdam, 1988.Google Scholar
Vesley, R. E., A palatable substitute for Kripke’s Schema , Intuitionism and Proof Theory: Proceedings of the Summer Conference at Buffalo N.Y. 1968 (Kino, A., Myhill, J., and Vesley, R. E., editors), North-Holland, 1970, pp. 197–207.CrossRefGoogle Scholar