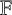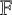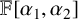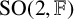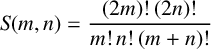1 Introduction
This is the second of our series of papers building an integration theory of polynomials over unit circles over a general field
![]() $\mathbb {F}$
. The first paper [Reference Limanta9] deals with the case where
$\mathbb {F}$
. The first paper [Reference Limanta9] deals with the case where
![]() $\mathbb {F}$
is finite of odd characteristic; the family of integers
$\mathbb {F}$
is finite of odd characteristic; the family of integers
![]() $S(m,n)$
called the super Catalan numbers and their closely related family of rational numbers
$S(m,n)$
called the super Catalan numbers and their closely related family of rational numbers
![]() $\Omega (m,n)$
called the circular super Catalan numbers play a prominent role. These numbers are defined by
$\Omega (m,n)$
called the circular super Catalan numbers play a prominent role. These numbers are defined by
and are indexed by two elements in
![]() $\mathbb {N}$
(the nonnegative integers including
$\mathbb {N}$
(the nonnegative integers including
![]() $0$
).
$0$
).
The super Catalan numbers were first introduced by Catalan [Reference Catalan3] in 1874 and the first modern study of these numbers was initiated by Gessel [Reference Gessel7] in 1992. They generalise the Catalan numbers
![]() $c_n$
since
$c_n$
since
![]() $S(1,n) = 2c_n$
. The integrality of
$S(1,n) = 2c_n$
. The integrality of
![]() $S(m,n)$
can be observed from the relation
$S(m,n)$
can be observed from the relation
![]() $4S(m,n) = S(m+1,n) + S(m,n+1)$
which yields the Pascal-like property
$4S(m,n) = S(m+1,n) + S(m,n+1)$
which yields the Pascal-like property
![]() $\Omega (m,n) = \Omega (m+1,n) + \Omega (m,n+1)$
.
$\Omega (m,n) = \Omega (m+1,n) + \Omega (m,n+1)$
.
No combinatorial interpretation of
![]() $S(m,n)$
is known for general m and n, in contrast to over
$S(m,n)$
is known for general m and n, in contrast to over
![]() $200$
interpretations of the Catalan numbers [Reference Stanley12]. However, for
$200$
interpretations of the Catalan numbers [Reference Stanley12]. However, for
![]() $m = 2$
, there are some interpretations in terms of cubic trees by Pippenger and Schleich [Reference Pippenger and Schleich10] and blossom trees by Schaeffer [Reference Schaeffer11], and when
$m = 2$
, there are some interpretations in terms of cubic trees by Pippenger and Schleich [Reference Pippenger and Schleich10] and blossom trees by Schaeffer [Reference Schaeffer11], and when
![]() $m = 2, 3$
, as pairs of Dyck paths with restricted heights by Gessel and Xin [Reference Gessel and Xin8]. When
$m = 2, 3$
, as pairs of Dyck paths with restricted heights by Gessel and Xin [Reference Gessel and Xin8]. When
![]() $n = m+s$
for
$n = m+s$
for
![]() $0\leq s\leq 3$
, Chen and Wang showed that there is an interpretation in terms of restricted lattice paths [Reference Chen and Wang4]. There is also a weighted interpretation of
$0\leq s\leq 3$
, Chen and Wang showed that there is an interpretation in terms of restricted lattice paths [Reference Chen and Wang4]. There is also a weighted interpretation of
![]() $S(m,n)$
as a certain value of Krawtchouk polynomials by the work of Georgiadis et al. [Reference Georgiadis, Munemasa and Tanaka6], and another in terms of positive and negative
$S(m,n)$
as a certain value of Krawtchouk polynomials by the work of Georgiadis et al. [Reference Georgiadis, Munemasa and Tanaka6], and another in terms of positive and negative
![]() $2$
-Motzkin paths by Allen and Gheorghiciuc [Reference Allen and Gheorghiciuc1].
$2$
-Motzkin paths by Allen and Gheorghiciuc [Reference Allen and Gheorghiciuc1].
The aim of this paper is twofold. The first is to build, in a rather elementary way, a polynomial integration theory over circles in the Euclidean geometry over general fields of characteristic zero without recourse to the usual Riemann integral and limiting processes. We shall see that this allows us to give the super Catalan numbers a purely algebraic interpretation, which is our second objective.
Here and throughout,
![]() $\mathbb {F}$
is a general field of characteristic zero with multiplicative identity
$\mathbb {F}$
is a general field of characteristic zero with multiplicative identity
![]() $1_{\mathbb {F}}$
or sometimes just
$1_{\mathbb {F}}$
or sometimes just
![]() $1$
if the context is clear. We denote by
$1$
if the context is clear. We denote by
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
the algebra of polynomials in
$\mathbb {F}[\alpha _1, \alpha _2]$
the algebra of polynomials in
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
over
$\alpha _2$
over
![]() $\mathbb {F}$
with multiplicative identity
$\mathbb {F}$
with multiplicative identity
![]() $\mathbf {1}$
. Our algebraic integral over a circle C is a linear functional
$\mathbf {1}$
. Our algebraic integral over a circle C is a linear functional
![]() $\phi $
on
$\phi $
on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
, called a circular integral functional with respect to C, which satisfies three conditions:
$\mathbb {F}[\alpha _1, \alpha _2]$
, called a circular integral functional with respect to C, which satisfies three conditions:
![]() $\phi (\mathbf {1}) = 1_{\mathbb {F}}$
(Normalisation),
$\phi (\mathbf {1}) = 1_{\mathbb {F}}$
(Normalisation),
![]() $\phi (\pi ) = 0$
whenever
$\phi (\pi ) = 0$
whenever
![]() $\pi $
evaluates to the zero function on C (Locality) and
$\pi $
evaluates to the zero function on C (Locality) and
![]() $\phi $
is rotationally invariant (Invariance).
$\phi $
is rotationally invariant (Invariance).
When
![]() $\mathbb {F} = \mathbb {R}$
, there is a well-known formula for the integral of polynomials on the unit sphere
$\mathbb {F} = \mathbb {R}$
, there is a well-known formula for the integral of polynomials on the unit sphere
![]() $S^{n-1}$
(see [Reference Baker2] or [Reference Folland5]).
$S^{n-1}$
(see [Reference Baker2] or [Reference Folland5]).
Theorem 1.1. Let
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $S^{n-1}$
denote the
$S^{n-1}$
denote the
![]() $(n-1)$
-dimensional unit sphere in
$(n-1)$
-dimensional unit sphere in
![]() $\mathbb {R}^{n}$
. If
$\mathbb {R}^{n}$
. If
![]() $\mu $
is the usual rotationally invariant measure on
$\mu $
is the usual rotationally invariant measure on
![]() $S^{n-1}$
, then by writing
$S^{n-1}$
, then by writing
![]() $b_i = \tfrac 12(d_i + 1)$
,
$b_i = \tfrac 12(d_i + 1)$
,
 $$ \begin{align*} \int_{S^{n-1}} x_{1}^{d_1} x_{2}^{d_2} \cdots x_n^{d_n}\, d\mu = \begin{cases} \dfrac{2}{\Gamma(b_1 + b_2 + \cdots + b_n )}{\displaystyle\prod\limits_{i=1}^{n}} \Gamma(b_i) &\text{if each } d_i \text{ is even}, \\ 0 &\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \int_{S^{n-1}} x_{1}^{d_1} x_{2}^{d_2} \cdots x_n^{d_n}\, d\mu = \begin{cases} \dfrac{2}{\Gamma(b_1 + b_2 + \cdots + b_n )}{\displaystyle\prod\limits_{i=1}^{n}} \Gamma(b_i) &\text{if each } d_i \text{ is even}, \\ 0 &\text{otherwise.} \end{cases} \end{align*} $$
We may obtain from Theorem 1.1, when
![]() $n = 2$
,
$n = 2$
,
![]() $d_1 = 2m$
and
$d_1 = 2m$
and
![]() $d_2 = 2n$
, that
$d_2 = 2n$
, that
 $$ \begin{align*} \frac{2\Gamma(b_1)\Gamma(b_2)}{\Gamma(b_1 + b_2)} = \frac{2\Gamma\big(m+\frac{1}{2}\big)\Gamma\big(n+\frac{1}{2}\big)}{\Gamma(m+n+1)} = 2\pi \frac{(2m)!(2n)!}{4^{m+n}m!n!(m+n)!} = 2\pi \Omega(m,n). \end{align*} $$
$$ \begin{align*} \frac{2\Gamma(b_1)\Gamma(b_2)}{\Gamma(b_1 + b_2)} = \frac{2\Gamma\big(m+\frac{1}{2}\big)\Gamma\big(n+\frac{1}{2}\big)}{\Gamma(m+n+1)} = 2\pi \frac{(2m)!(2n)!}{4^{m+n}m!n!(m+n)!} = 2\pi \Omega(m,n). \end{align*} $$
So if the integral is normalised, we get just the circular super Catalan numbers.
In [Reference Limanta9], we showed that the polynomial integration theory over a finite field of odd characteristic is analogous to the
![]() $\mathbb {F} = \mathbb {R}$
case, which we summarise in the next theorem.
$\mathbb {F} = \mathbb {R}$
case, which we summarise in the next theorem.
Theorem 1.2. Let
![]() $p>2$
be a prime and
$p>2$
be a prime and
![]() $q = p^r$
for some
$q = p^r$
for some
![]() $r \in \mathbb {N}$
. In the Euclidean geometry over
$r \in \mathbb {N}$
. In the Euclidean geometry over
![]() $\mathbb {F}_{q}$
with multiplicative identity
$\mathbb {F}_{q}$
with multiplicative identity
![]() $1_q$
, the unit circle is defined by
$1_q$
, the unit circle is defined by
![]() ${S^1 = \{(x_1,x_2) \in \mathbb {F}_q^2 \ \colon x_1^2 + x_2^2 = 1_q\}}$
. Let k and
${S^1 = \{(x_1,x_2) \in \mathbb {F}_q^2 \ \colon x_1^2 + x_2^2 = 1_q\}}$
. Let k and
![]() $\ell $
be any natural numbers for which
$\ell $
be any natural numbers for which
![]() $0 \leq k+\ell < q-1$
. Then the functional
$0 \leq k+\ell < q-1$
. Then the functional
![]() $\psi _{b,q}$
on
$\psi _{b,q}$
on
![]() $\mathbb {F}_q[\alpha _1, \alpha _2]$
given by
$\mathbb {F}_q[\alpha _1, \alpha _2]$
given by
 $$ \begin{align*} \psi_{b,q}(\alpha_1^{k}\alpha_2^{\ell}) = -\bigg(\frac{-1}{p}\bigg)^r \sum_{(x_1,x_2) \in S^1} x_1^k x_2^\ell = \begin{cases} \Omega(m,n) \bmod p &\mbox{if } k=2m \mbox{ and } \ell=2n, \\ 0 & \mbox{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} \psi_{b,q}(\alpha_1^{k}\alpha_2^{\ell}) = -\bigg(\frac{-1}{p}\bigg)^r \sum_{(x_1,x_2) \in S^1} x_1^k x_2^\ell = \begin{cases} \Omega(m,n) \bmod p &\mbox{if } k=2m \mbox{ and } \ell=2n, \\ 0 & \mbox{otherwise}, \end{cases} \end{align*} $$
is the unique circular integral functional with respect to
![]() $S^1$
. Here
$S^1$
. Here
![]() $(\frac {-1}{p})$
is the usual Legendre symbol.
$(\frac {-1}{p})$
is the usual Legendre symbol.
Now we present our main result. For
![]() $a \in \mathbb {Q}$
, we denote by
$a \in \mathbb {Q}$
, we denote by
![]() $a1_{\mathbb {F}}$
the embedding of a in
$a1_{\mathbb {F}}$
the embedding of a in
![]() $\mathbb {F}$
. The unit circle
$\mathbb {F}$
. The unit circle
![]() $S^1$
in this setting will be defined in the next section.
$S^1$
in this setting will be defined in the next section.
Theorem 1.3. For any
![]() $k, l \in \mathbb {N}$
, the linear functional
$k, l \in \mathbb {N}$
, the linear functional
![]() $\psi $
on
$\psi $
on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
defined by
$\mathbb {F}[\alpha _1, \alpha _2]$
defined by
 $$ \begin{align*} \psi(\alpha_1^k \alpha_2^\ell) = \begin{cases} \Omega(m,n) 1_{\mathbb{F}} & \mbox{if}\ k = 2m\ \mbox{and}\ \ell = 2n, \\ 0 & \mbox{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} \psi(\alpha_1^k \alpha_2^\ell) = \begin{cases} \Omega(m,n) 1_{\mathbb{F}} & \mbox{if}\ k = 2m\ \mbox{and}\ \ell = 2n, \\ 0 & \mbox{otherwise}, \end{cases} \end{align*} $$
is the unique circular integral functional with respect to
![]() $S^1$
.
$S^1$
.
2 Circular integral functional
Denote by
![]() $\mathbb {A} = \mathbb {A}(\mathbb {F})$
the two-dimensional affine plane
$\mathbb {A} = \mathbb {A}(\mathbb {F})$
the two-dimensional affine plane
![]() $\{(x_1,x_2) : x,y \in \mathbb {F} \}$
, with the objects
$\{(x_1,x_2) : x,y \in \mathbb {F} \}$
, with the objects
![]() $(x_1,x_2)$
called points. The space
$(x_1,x_2)$
called points. The space
![]() $\mathbb {F}^{\mathbb {A}}$
consists of functions from
$\mathbb {F}^{\mathbb {A}}$
consists of functions from
![]() $\mathbb {A}$
to
$\mathbb {A}$
to
![]() $\mathbb {F}$
, and is an
$\mathbb {F}$
, and is an
![]() $\mathbb {F}$
-algebra under pointwise addition and multiplication and with the evaluation map
$\mathbb {F}$
-algebra under pointwise addition and multiplication and with the evaluation map
![]() $\varepsilon \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}^{\mathbb {A}}$
which is an algebra homomorphism. Clearly we may regard
$\varepsilon \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}^{\mathbb {A}}$
which is an algebra homomorphism. Clearly we may regard
![]() $\mathbb {F}[\alpha _1]$
as a subalgebra of
$\mathbb {F}[\alpha _1]$
as a subalgebra of
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
. Recall that any nonzero polynomial in
$\mathbb {F}[\alpha _1, \alpha _2]$
. Recall that any nonzero polynomial in
![]() $\mathbb {F}[\alpha _1]$
of degree d has at most d roots.
$\mathbb {F}[\alpha _1]$
of degree d has at most d roots.
The group
![]() $\mathrm {GL}(2,\mathbb {F})$
of invertible
$\mathrm {GL}(2,\mathbb {F})$
of invertible
![]() $2 \times 2$
matrices with entries in
$2 \times 2$
matrices with entries in
![]() $\mathbb {F}$
left-acts on
$\mathbb {F}$
left-acts on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
as follows: if
$\mathbb {F}[\alpha _1, \alpha _2]$
as follows: if
![]() $\pi = \pi (\alpha _1, \alpha _2)$
, then
$\pi = \pi (\alpha _1, \alpha _2)$
, then
 $$ \begin{align} h \cdot \pi = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}\cdot \pi := \pi ( h_{11}\alpha_1 +h_{21}\alpha_2 , h_{12}\alpha_1 + h_{22}\alpha_2 ). \end{align} $$
$$ \begin{align} h \cdot \pi = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}\cdot \pi := \pi ( h_{11}\alpha_1 +h_{21}\alpha_2 , h_{12}\alpha_1 + h_{22}\alpha_2 ). \end{align} $$
Additionally,
![]() $\mathrm {GL}(2,\mathbb {F})$
right-acts on
$\mathrm {GL}(2,\mathbb {F})$
right-acts on
![]() $\mathbb {A}$
and left-acts on
$\mathbb {A}$
and left-acts on
![]() $\mathbb {F}^{\mathbb {A}}$
as follows:
$\mathbb {F}^{\mathbb {A}}$
as follows:
 $$ \begin{align*} (x_1, x_2) \cdot h &:= (h_{11}x_1 + h_{21} x_2, h_{12}x_1 + h_{22} x_2), \\ (h \cdot f)(x_1, x_2) &:= f((x_1,x_2) \cdot h) = f(h_{11}x_1 + h_{21} x_2, h_{12}x_1 + h_{22} x_2). \end{align*} $$
$$ \begin{align*} (x_1, x_2) \cdot h &:= (h_{11}x_1 + h_{21} x_2, h_{12}x_1 + h_{22} x_2), \\ (h \cdot f)(x_1, x_2) &:= f((x_1,x_2) \cdot h) = f(h_{11}x_1 + h_{21} x_2, h_{12}x_1 + h_{22} x_2). \end{align*} $$
The group
![]() $\mathrm {SO}(2,\mathbb {F})$
of matrices h that satisfy
$\mathrm {SO}(2,\mathbb {F})$
of matrices h that satisfy
![]() $h^{-1} = h^{T}$
of determinant
$h^{-1} = h^{T}$
of determinant
![]() $1_{\mathbb {F}}$
is a subgroup of
$1_{\mathbb {F}}$
is a subgroup of
![]() $\mathrm {GL}(2,\mathbb {F})$
and is called the rotation group. The action of
$\mathrm {GL}(2,\mathbb {F})$
and is called the rotation group. The action of
![]() $\mathrm {SO}(2,\mathbb {F})$
on
$\mathrm {SO}(2,\mathbb {F})$
on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
is induced as the restriction of the action of
$\mathbb {F}[\alpha _1, \alpha _2]$
is induced as the restriction of the action of
![]() $\mathrm {GL}(2,\mathbb {F})$
on
$\mathrm {GL}(2,\mathbb {F})$
on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
. This action respects evaluation: for any
$\mathbb {F}[\alpha _1, \alpha _2]$
. This action respects evaluation: for any
![]() $h \in \mathrm {SO}(2,\mathbb {F})$
and
$h \in \mathrm {SO}(2,\mathbb {F})$
and
![]() $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
,
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
,
In a similar manner, we also get an action of
![]() $\mathrm {SO}(2,\mathbb {F})$
on
$\mathrm {SO}(2,\mathbb {F})$
on
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {F}^{\mathbb {A}}$
.
$\mathbb {F}^{\mathbb {A}}$
.
We define a symmetric bilinear form on
![]() $\mathbb {A}$
, given by
$\mathbb {A}$
, given by
![]() $(x_1, x_2) \cdot (y_1, y_2) := x_1y_1 + x_2y_2$
. The associated quadratic form gives rise to the (Euclidean) unit circle
$(x_1, x_2) \cdot (y_1, y_2) := x_1y_1 + x_2y_2$
. The associated quadratic form gives rise to the (Euclidean) unit circle
Lemma 2.1. Each point on
![]() $S^1$
except
$S^1$
except
![]() $(-1,0)$
can be written as
$(-1,0)$
can be written as
 $$ \begin{align*}\bigg(\frac{1-u^{2}}{1+u^{2}},\frac{2u}{1+u^{2}}\bigg)\end{align*} $$
$$ \begin{align*}\bigg(\frac{1-u^{2}}{1+u^{2}},\frac{2u}{1+u^{2}}\bigg)\end{align*} $$
for some
![]() $u\in \mathbb {F}$
such that
$u\in \mathbb {F}$
such that
![]() $1+u^2 \neq 0$
. Consequently,
$1+u^2 \neq 0$
. Consequently,
![]() $S^1$
is an infinite set.
$S^1$
is an infinite set.
Proof. The identity
![]() $({(1-u^{2})}/{(1+u^{2})})^{2} + ({2u}/{(1+u^{2})})^{2}=1_{\mathbb {F}}$
holds for all
$({(1-u^{2})}/{(1+u^{2})})^{2} + ({2u}/{(1+u^{2})})^{2}=1_{\mathbb {F}}$
holds for all
![]() $u \in \mathbb {F}$
for which
$u \in \mathbb {F}$
for which
![]() $u^2 \neq -1$
. The line
$u^2 \neq -1$
. The line
![]() $x_2=ux_1+u$
through the points
$x_2=ux_1+u$
through the points
![]() $(-1,0)$
and
$(-1,0)$
and
![]() $(0,u)$
intersects
$(0,u)$
intersects
![]() $S^1$
at exactly two points,
$S^1$
at exactly two points,
![]() $(-1,0)$
and
$(-1,0)$
and
![]() $({(1-u^{2})}/{(1+u^{2})}, {2u}/{(1+u^{2})})$
. Hence, every point on
$({(1-u^{2})}/{(1+u^{2})}, {2u}/{(1+u^{2})})$
. Hence, every point on
![]() $S^1$
except
$S^1$
except
![]() $(-1,0)$
corresponds to exactly one
$(-1,0)$
corresponds to exactly one
![]() $u \in \mathbb {F}$
for which
$u \in \mathbb {F}$
for which
![]() $u^2 \neq -1$
. Since there are infinitely many
$u^2 \neq -1$
. Since there are infinitely many
![]() $u \in \mathbb {F}$
for which
$u \in \mathbb {F}$
for which
![]() $u^2 \neq -1$
,
$u^2 \neq -1$
,
![]() $S^1$
is an infinite set.
$S^1$
is an infinite set.
Corollary 2.2. The rotation group
![]() $\mathrm {SO}(2,\mathbb {F})$
admits a parametrisation
$\mathrm {SO}(2,\mathbb {F})$
admits a parametrisation
 $$ \begin{align*} \mathrm{SO}(2,\mathbb{F}) =\left\{h_u = \frac{1}{1+u^{2}} \begin{pmatrix} 1-u^{2} & -2u \\ 2u & 1-u^{2} \end{pmatrix} \colon \ u \in \mathbb{F}, u^2 \neq -1\right\} \cup \{-I\}. \end{align*} $$
$$ \begin{align*} \mathrm{SO}(2,\mathbb{F}) =\left\{h_u = \frac{1}{1+u^{2}} \begin{pmatrix} 1-u^{2} & -2u \\ 2u & 1-u^{2} \end{pmatrix} \colon \ u \in \mathbb{F}, u^2 \neq -1\right\} \cup \{-I\}. \end{align*} $$
We now introduce the central object of this paper: a linear functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
that generalises normalised integration over the Euclidean unit circle over
$\mathbb {F}[\alpha _1, \alpha _2]$
that generalises normalised integration over the Euclidean unit circle over
![]() $\mathbb {R}$
. We say that a linear functional
$\mathbb {R}$
. We say that a linear functional
![]() $\phi \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}$
is a circular integral functional on
$\phi \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}$
is a circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1$
precisely when it satisfies the following three conditions.
$S^1$
precisely when it satisfies the following three conditions.
-
(Normalisation) For the multiplicative identity
 $\mathbf {1}$
of
$\mathbf {1}$
of
 $\mathbb {F}[\alpha _1, \alpha _2]$
, we have
$\mathbb {F}[\alpha _1, \alpha _2]$
, we have
 $\phi (\mathbf {1}) = 1_{\mathbb {F}}$
.
$\phi (\mathbf {1}) = 1_{\mathbb {F}}$
. -
(Locality) If
 $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
such that
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
such that
 $\varepsilon (\pi )$
is the zero function on
$\varepsilon (\pi )$
is the zero function on
 $S^1$
, then
$S^1$
, then
 $\phi (\pi ) = 0$
.
$\phi (\pi ) = 0$
. -
(Invariance) The functional
 $\phi $
is
$\phi $
is
 $\mathrm {SO}(2,\mathbb {F})$
-invariant:
$\mathrm {SO}(2,\mathbb {F})$
-invariant:
 $\phi (h \cdot \pi ) = \phi (\pi )$
holds for any
$\phi (h \cdot \pi ) = \phi (\pi )$
holds for any
 $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
and
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
and
 $h \in \mathrm {SO}(2,\mathbb {F})$
.
$h \in \mathrm {SO}(2,\mathbb {F})$
.
3 Existence and uniqueness
Our strategy to prove Theorem 1.3 is divided into two main steps. First, we show that
![]() $\psi $
satisfies the Normalisation, Locality and Invariance conditions. Next, we demonstrate that if such a circular integral functional
$\psi $
satisfies the Normalisation, Locality and Invariance conditions. Next, we demonstrate that if such a circular integral functional
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1$
exists, it is uniquely determined.
$S^1$
exists, it is uniquely determined.
It is easy to see that the Normalisation condition holds. The next two lemmas are needed to prove the Locality of
![]() $\psi $
.
$\psi $
.
Lemma 3.1. Both
![]() $S^1_{x_1} = \{x_2 \in \mathbb {F} : (x_1,x_2) \in S^1\}$
and
$S^1_{x_1} = \{x_2 \in \mathbb {F} : (x_1,x_2) \in S^1\}$
and
![]() $S^1_{x_2} = \{x_1 \in \mathbb {F} : (x_1,x_2) \in S^1\}$
have infinitely many elements.
$S^1_{x_2} = \{x_1 \in \mathbb {F} : (x_1,x_2) \in S^1\}$
have infinitely many elements.
Proof. For any
![]() $(x_1,x_2) \in S^1$
, we have that
$(x_1,x_2) \in S^1$
, we have that
![]() $(x_2,x_1) \in S^1$
, so
$(x_2,x_1) \in S^1$
, so
![]() $S^1_{x_1} = S^1_{x_2}$
. If
$S^1_{x_1} = S^1_{x_2}$
. If
![]() $S^1_{x_1} = S^1_{x_2}$
is finite, then so is
$S^1_{x_1} = S^1_{x_2}$
is finite, then so is
![]() $S^1_{x_1} \times S^1_{x_2}$
and consequently
$S^1_{x_1} \times S^1_{x_2}$
and consequently
![]() $S^1$
. This contradicts the fact that
$S^1$
. This contradicts the fact that
![]() $S^1$
is infinite from Lemma 2.1.
$S^1$
is infinite from Lemma 2.1.
The crucial property of polynomials in
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
that evaluate to the zero function on
$\mathbb {F}[\alpha _1, \alpha _2]$
that evaluate to the zero function on
![]() $S^1$
is that they must lie in
$S^1$
is that they must lie in
![]() $\langle \alpha _1^2 + \alpha _2^2 -1\rangle $
, the ideal generated by
$\langle \alpha _1^2 + \alpha _2^2 -1\rangle $
, the ideal generated by
![]() $\alpha _1^2 + \alpha _2^2 -1$
. We offer an elementary proof below by using the multivariate polynomial division which requires a choice of monomial ordering. This has a flavour of Hilbert’s Nullstellensatz which usually works over algebraically closed fields, although our argument does not assume that
$\alpha _1^2 + \alpha _2^2 -1$
. We offer an elementary proof below by using the multivariate polynomial division which requires a choice of monomial ordering. This has a flavour of Hilbert’s Nullstellensatz which usually works over algebraically closed fields, although our argument does not assume that
![]() $\mathbb {F}$
is an algebraically closed field.
$\mathbb {F}$
is an algebraically closed field.
Lemma 3.2. If
![]() $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
satisfies
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
satisfies
![]() $\varepsilon (\pi ) = 0$
on
$\varepsilon (\pi ) = 0$
on
![]() $S^1$
, then
$S^1$
, then
![]() $\pi \in \langle \alpha _1^2+\alpha _2^2-1\rangle $
.
$\pi \in \langle \alpha _1^2+\alpha _2^2-1\rangle $
.
Proof. Fix a monomial ordering
![]() $\preccurlyeq $
such that
$\preccurlyeq $
such that
![]() $\alpha _1^{k_1}\alpha _2^{\ell _1} \preccurlyeq \alpha _1^{k_2}\alpha _2^{\ell _2}$
if either
$\alpha _1^{k_1}\alpha _2^{\ell _1} \preccurlyeq \alpha _1^{k_2}\alpha _2^{\ell _2}$
if either
![]() $k_1 < k_2$
or
$k_1 < k_2$
or
![]() ${k_1 = k_2}$
and
${k_1 = k_2}$
and
![]() $\ell _1 < \ell _2$
. With respect to this ordering, any
$\ell _1 < \ell _2$
. With respect to this ordering, any
![]() $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
can be written as
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
can be written as
![]() $\pi = (\alpha _1^2 + \alpha _2^2 - 1) \pi _{0} + \alpha _2 \omega + \rho $
for some
$\pi = (\alpha _1^2 + \alpha _2^2 - 1) \pi _{0} + \alpha _2 \omega + \rho $
for some
![]() $\pi _{0} \in \mathbb {F}[\alpha _1, \alpha _2]$
and
$\pi _{0} \in \mathbb {F}[\alpha _1, \alpha _2]$
and
![]() $\omega , \rho \in \mathbb {F}[\alpha _1]$
.
$\omega , \rho \in \mathbb {F}[\alpha _1]$
.
Since
![]() $\pi $
evaluates to the zero function on
$\pi $
evaluates to the zero function on
![]() $S^1$
,
$S^1$
,
for all
![]() $(x_1,x_2) \in S^1$
, where the last equation holds because
$(x_1,x_2) \in S^1$
, where the last equation holds because
![]() $\omega , \rho \in \mathbb {F}[\alpha _1]$
. Now consider the set
$\omega , \rho \in \mathbb {F}[\alpha _1]$
. Now consider the set
![]() $S^1_\ast = \{(x_1,x_2) \in S^1 \, \colon x_2 \neq 0\}$
which is nonempty since
$S^1_\ast = \{(x_1,x_2) \in S^1 \, \colon x_2 \neq 0\}$
which is nonempty since
![]() $(0,1) \in S^1_\ast $
. For any
$(0,1) \in S^1_\ast $
. For any
![]() $(x_1,x_2) \in S^1_\ast $
, the point
$(x_1,x_2) \in S^1_\ast $
, the point
![]() $(x_1,-x_2) \in S^1_\ast $
is different from
$(x_1,-x_2) \in S^1_\ast $
is different from
![]() $(x_1,x_2)$
so (3.1) forces
$(x_1,x_2)$
so (3.1) forces
![]() $\varepsilon (\omega )(x_1, 0) = \varepsilon (\rho )(x_1, 0) = 0$
for all
$\varepsilon (\omega )(x_1, 0) = \varepsilon (\rho )(x_1, 0) = 0$
for all
![]() $(x_1, x_2) \in S^1$
. By Lemma 3.1,
$(x_1, x_2) \in S^1$
. By Lemma 3.1,
![]() $\omega $
and
$\omega $
and
![]() $\rho $
have infinitely many roots, so they must be the zero polynomial.
$\rho $
have infinitely many roots, so they must be the zero polynomial.
Theorem 3.3 (Locality of
 $ \psi $
).
$ \psi $
).
The linear functional
![]() $\psi $
satisfies the Locality condition.
$\psi $
satisfies the Locality condition.
Proof. If
![]() $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
evaluates to the zero function on
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
evaluates to the zero function on
![]() $S^1$
, then
$S^1$
, then
![]() $\pi \in \langle \alpha _1^{2} + \alpha _2^{2}-1\rangle $
from Lemma 3.2. By linearity, it suffices to show that
$\pi \in \langle \alpha _1^{2} + \alpha _2^{2}-1\rangle $
from Lemma 3.2. By linearity, it suffices to show that
vanishes. Clearly it does if either k or
![]() $\ell $
is odd, and if
$\ell $
is odd, and if
![]() $k = 2m$
and
$k = 2m$
and
![]() $\ell = 2n$
, the right- hand side simplifies to
$\ell = 2n$
, the right- hand side simplifies to
![]() $\Omega (m+1,n) + \Omega (m,n+1) - \Omega (m,n) = 0$
by the Pascal-like property.
$\Omega (m+1,n) + \Omega (m,n+1) - \Omega (m,n) = 0$
by the Pascal-like property.
Finally, to prove the Invariance of
![]() $\psi $
, we need the following three lemmas.
$\psi $
, we need the following three lemmas.
Lemma 3.4. For any
![]() $h \in \mathrm {SO}(2,\mathbb {F})$
and natural numbers
$h \in \mathrm {SO}(2,\mathbb {F})$
and natural numbers
![]() $k, \ell $
, each term of
$k, \ell $
, each term of
![]() $h \cdot \alpha _1^k\alpha _2^\ell $
has degree
$h \cdot \alpha _1^k\alpha _2^\ell $
has degree
![]() $k+\ell $
.
$k+\ell $
.
Proof. By using (2.1),
![]() $h \cdot \alpha _1^k \alpha _2^\ell = (h_{11} \alpha _1 + h_{21} \alpha _2)^k (h_{12} \alpha _1 + h_{22} \alpha _2)^\ell $
. Expanding this using the binomial theorem, we see that the degree of each term is always
$h \cdot \alpha _1^k \alpha _2^\ell = (h_{11} \alpha _1 + h_{21} \alpha _2)^k (h_{12} \alpha _1 + h_{22} \alpha _2)^\ell $
. Expanding this using the binomial theorem, we see that the degree of each term is always
![]() $k+\ell $
.
$k+\ell $
.
Lemma 3.5. For any natural numbers m and
![]() $h \in \mathrm {SO}(2,\mathbb {F})$
, we have
$h \in \mathrm {SO}(2,\mathbb {F})$
, we have
![]() $\psi (h \cdot \alpha _1^{2m}) = \psi (\alpha _1^{2m})$
and
$\psi (h \cdot \alpha _1^{2m}) = \psi (\alpha _1^{2m})$
and
![]() $\psi (h \cdot \alpha _1^{2m-1}\alpha _2) = \psi (\alpha ^{2m-1}\alpha _2)$
.
$\psi (h \cdot \alpha _1^{2m-1}\alpha _2) = \psi (\alpha ^{2m-1}\alpha _2)$
.
Proof. The statement is obviously true for
![]() $h = -I$
. Now for
$h = -I$
. Now for
![]() $h = h_u$
defined in Corollary 2.2,
$h = h_u$
defined in Corollary 2.2,
 $$ \begin{align*} \psi(h_{u} \cdot \alpha_1^{2m}) = \sum_{s=0}^{2m} \binom{2m}{s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-s} \psi(\alpha_1^{s} \alpha_2^{2m-s}). \end{align*} $$
$$ \begin{align*} \psi(h_{u} \cdot \alpha_1^{2m}) = \sum_{s=0}^{2m} \binom{2m}{s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-s} \psi(\alpha_1^{s} \alpha_2^{2m-s}). \end{align*} $$
However, since the odd indices do not contribute to the sum, we just need to consider the even indices:
 $$ \begin{align} \psi(h_{u} \cdot \alpha_1^{2m}) &= \sum_{s=0}^{m} \binom{2m}{2s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} \psi(\alpha_1^{2s}\alpha_2^{2m-2s}) \nonumber \\ &= \sum_{s=0}^{m} \binom{2m}{2s} \Omega(s,m-s) \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} 1_{\mathbb{F}} \nonumber \\ & =\frac{(2m)!}{4^{m}m!m!} \sum_{s=0}^{m} \binom{m}{s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s}\bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} 1_{\mathbb{F}}. \end{align} $$
$$ \begin{align} \psi(h_{u} \cdot \alpha_1^{2m}) &= \sum_{s=0}^{m} \binom{2m}{2s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} \psi(\alpha_1^{2s}\alpha_2^{2m-2s}) \nonumber \\ &= \sum_{s=0}^{m} \binom{2m}{2s} \Omega(s,m-s) \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s} \bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} 1_{\mathbb{F}} \nonumber \\ & =\frac{(2m)!}{4^{m}m!m!} \sum_{s=0}^{m} \binom{m}{s} \bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2s}\bigg(\frac{2u}{1+u^{2}}\bigg)^{2m-2s} 1_{\mathbb{F}}. \end{align} $$
Using the binomial theorem, (3.2) simplifies to
 $$ \begin{align*} \psi(\alpha_1^{2m}) \bigg(\bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2} + \bigg(\frac{2u}{1+u^{2}}\bigg)^{2}\bigg)^{m} = \psi(\alpha_1^{2m})1_{\mathbb{F}}. \end{align*} $$
$$ \begin{align*} \psi(\alpha_1^{2m}) \bigg(\bigg(\frac{1-u^{2}}{1+u^{2}}\bigg)^{2} + \bigg(\frac{2u}{1+u^{2}}\bigg)^{2}\bigg)^{m} = \psi(\alpha_1^{2m})1_{\mathbb{F}}. \end{align*} $$
The proof that
![]() $\psi (h_{u} \cdot \alpha _1^{2m-1}\alpha _2) = \psi (\alpha _1^{2m-1}\alpha _2)$
is more involved but done similarly.
$\psi (h_{u} \cdot \alpha _1^{2m-1}\alpha _2) = \psi (\alpha _1^{2m-1}\alpha _2)$
is more involved but done similarly.
Lemma 3.6. If
![]() $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
evaluates to the zero function on
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
evaluates to the zero function on
![]() $S^1$
, then so does
$S^1$
, then so does
![]() $h \cdot \pi $
for any
$h \cdot \pi $
for any
![]() $h \in \mathrm {SO}(2,\mathbb {F})$
.
$h \in \mathrm {SO}(2,\mathbb {F})$
.
Proof. For an arbitrary
![]() $h \in \mathrm {SO}(2,\mathbb {F})$
, the map
$h \in \mathrm {SO}(2,\mathbb {F})$
, the map
![]() $(x_1, x_2) \mapsto (x_1,x_2) \cdot h$
is a bijection on
$(x_1, x_2) \mapsto (x_1,x_2) \cdot h$
is a bijection on
![]() $S^1$
. Choose any
$S^1$
. Choose any
![]() $(x_1, x_2) \in S^1$
. Then
$(x_1, x_2) \in S^1$
. Then
![]() $(x_1,x_2) = (u_1,u_2) \cdot h^{-1}$
for some
$(x_1,x_2) = (u_1,u_2) \cdot h^{-1}$
for some
![]() $(u_1,u_2) \in S^1$
. Using (2.2),
$(u_1,u_2) \in S^1$
. Using (2.2),
where the last equality follows from the assumption on
![]() $\pi $
. Consequently,
$\pi $
. Consequently,
![]() $h \cdot \pi $
evaluates to the zero function on
$h \cdot \pi $
evaluates to the zero function on
![]() $S^1$
.
$S^1$
.
Theorem 3.7 (Invariance of
 $ \psi $
).
$ \psi $
).
The linear functional
![]() $\psi $
satisfies the Invariance condition.
$\psi $
satisfies the Invariance condition.
Proof. It is sufficient to show that
![]() $\psi (h \cdot \alpha _1^{k}\alpha _2^{\ell }) = \psi (\alpha _1^{k}\alpha _2^{\ell })$
for any
$\psi (h \cdot \alpha _1^{k}\alpha _2^{\ell }) = \psi (\alpha _1^{k}\alpha _2^{\ell })$
for any
![]() $k,\ell \in \mathbb {N}$
and
$k,\ell \in \mathbb {N}$
and
![]() ${h \in \mathrm {SO}(2,\mathbb {F})}$
. As before, the statement is obviously true for
${h \in \mathrm {SO}(2,\mathbb {F})}$
. As before, the statement is obviously true for
![]() $h=-I$
, so we will only show that
$h=-I$
, so we will only show that
![]() $\psi (h_{u} \cdot \alpha _1^{k}\alpha _2^{\ell }) = \psi (\alpha _1^{k} \alpha _2^{\ell })$
. If
$\psi (h_{u} \cdot \alpha _1^{k}\alpha _2^{\ell }) = \psi (\alpha _1^{k} \alpha _2^{\ell })$
. If
![]() $k+\ell $
is odd, then by Lemma 3.4, each term of
$k+\ell $
is odd, then by Lemma 3.4, each term of
![]() $h_u \cdot \alpha _1^k \alpha _2^\ell $
has an odd degree and therefore
$h_u \cdot \alpha _1^k \alpha _2^\ell $
has an odd degree and therefore
![]() $\psi (h_{u} \cdot \alpha _1^{k} \alpha _2^{\ell }) = 0 = \psi (\alpha _1^{k}\alpha _2^{\ell })$
.
$\psi (h_{u} \cdot \alpha _1^{k} \alpha _2^{\ell }) = 0 = \psi (\alpha _1^{k}\alpha _2^{\ell })$
.
The polynomial
![]() $\pi = \alpha _1^{2m}\alpha _2^{2n} - \alpha _1^{2m} (1-\alpha _1^{2})^{n}$
evaluates to the zero function on
$\pi = \alpha _1^{2m}\alpha _2^{2n} - \alpha _1^{2m} (1-\alpha _1^{2})^{n}$
evaluates to the zero function on
![]() $S^1$
and therefore by Lemma 3.6,
$S^1$
and therefore by Lemma 3.6,
 $$ \begin{align*} \psi( h_{u} \cdot \alpha_1^{2m}\alpha_2^{2n}) =& \psi(h_{u}\cdot \alpha_1^{2m} (1-\alpha_1^{2})^{n}) = \sum_{s=0}^{n} (-1)^{s} \binom{n}{s} \psi (h_{u} \cdot \alpha_1^{2m+2s}). \end{align*} $$
$$ \begin{align*} \psi( h_{u} \cdot \alpha_1^{2m}\alpha_2^{2n}) =& \psi(h_{u}\cdot \alpha_1^{2m} (1-\alpha_1^{2})^{n}) = \sum_{s=0}^{n} (-1)^{s} \binom{n}{s} \psi (h_{u} \cdot \alpha_1^{2m+2s}). \end{align*} $$
Now by Lemma 3.5,
![]() $\psi (h_{u} \cdot \alpha _1^{2m+2s}) = \psi (\alpha _1^{2m+2s})$
and therefore this lets us retrace the steps:
$\psi (h_{u} \cdot \alpha _1^{2m+2s}) = \psi (\alpha _1^{2m+2s})$
and therefore this lets us retrace the steps:
 $$ \begin{align*} \psi(h_{u} \cdot \alpha_1^{2m} \alpha_2^{2n}) = \sum_{s=0}^{n} (-1)^{s} \binom{n}{s} \psi(\alpha_1^{2m+2s}) = \psi(\alpha_1^{2m} (1-\alpha_1^{2})^{n}) = \psi(\alpha_1^{2m}\alpha_2^{2n}), \end{align*} $$
$$ \begin{align*} \psi(h_{u} \cdot \alpha_1^{2m} \alpha_2^{2n}) = \sum_{s=0}^{n} (-1)^{s} \binom{n}{s} \psi(\alpha_1^{2m+2s}) = \psi(\alpha_1^{2m} (1-\alpha_1^{2})^{n}) = \psi(\alpha_1^{2m}\alpha_2^{2n}), \end{align*} $$
where in the last equality, we used the Locality of
![]() $\pi $
again. The case when k and
$\pi $
again. The case when k and
![]() $\ell $
are both odd is treated similarly. The conclusion thus follows by the linearity of
$\ell $
are both odd is treated similarly. The conclusion thus follows by the linearity of
![]() $\psi $
.
$\psi $
.
Next, we proceed to show that
![]() $\psi $
is the only circular integral functional on
$\psi $
is the only circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1$
.
$S^1$
.
Theorem 3.8 (Existence implies uniqueness).
If
![]() $\phi $
is any circular integral functional on
$\phi $
is any circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1$
, then
$S^1$
, then
![]() $\phi $
is uniquely determined.
$\phi $
is uniquely determined.
Proof. By linearity, it suffices to show that
![]() $\phi (\alpha _1^{k} \alpha _2^{\ell })$
is uniquely determined for any
$\phi (\alpha _1^{k} \alpha _2^{\ell })$
is uniquely determined for any
![]() $k,\ell \in \mathbb {N}$
. Using the Invariance property with
$k,\ell \in \mathbb {N}$
. Using the Invariance property with
![]() $h=-I$
, we obtain
$h=-I$
, we obtain
![]() $\phi (\alpha _1^{k}\alpha _2^{\ell }) = \phi (-I \cdot \alpha _1^{k}\alpha _2^{\ell }) = (-1)^{k+\ell }\phi (\alpha _1^{k} \alpha _2^{\ell })$
, so
$\phi (\alpha _1^{k}\alpha _2^{\ell }) = \phi (-I \cdot \alpha _1^{k}\alpha _2^{\ell }) = (-1)^{k+\ell }\phi (\alpha _1^{k} \alpha _2^{\ell })$
, so
![]() $\phi (\alpha _1^{k}\alpha _2^{\ell }) =0$
whenever
$\phi (\alpha _1^{k}\alpha _2^{\ell }) =0$
whenever
![]() $k+\ell $
is odd.
$k+\ell $
is odd.
For
![]() $m \ge 1$
, another application of the Invariance property with
$m \ge 1$
, another application of the Invariance property with
![]() $h = h_u$
from Corollary 2.2 gives
$h = h_u$
from Corollary 2.2 gives
 $$ \begin{align*} \phi(\alpha_1^{2m}) = \phi( h_{u} \cdot \alpha_1^{2m}) = \frac{1}{(1+u^{2})^{2m}} \sum_{s=0}^{2m} \binom{2m}{s} (1-u^{2})^{s} (2u)^{2m-s} \phi(\alpha_1^{s} \alpha_2^{2m-s}). \end{align*} $$
$$ \begin{align*} \phi(\alpha_1^{2m}) = \phi( h_{u} \cdot \alpha_1^{2m}) = \frac{1}{(1+u^{2})^{2m}} \sum_{s=0}^{2m} \binom{2m}{s} (1-u^{2})^{s} (2u)^{2m-s} \phi(\alpha_1^{s} \alpha_2^{2m-s}). \end{align*} $$
We multiply both sides by
![]() $(1+u^{2})^{2m}$
and split the summation depending on the parity of s to obtain
$(1+u^{2})^{2m}$
and split the summation depending on the parity of s to obtain
 $$ \begin{align} (1+u^{2})^{2m} \phi(\alpha_1^{2m}) &= \sum_{s=0}^{m} \binom{2m}{2s} (1-u^{2})^{2s} (2u)^{2m-2s} \phi(\alpha_1^{2s} \alpha_2^{2m-2s}) \notag \\ & \quad + \sum_{s=1}^{m} \binom{2m}{2s-1} (1-u^{2})^{2s-1} (2u)^{2m-2s+1} \phi(\alpha_1^{2s-1} \alpha_2^{2m-2s+1}). \end{align} $$
$$ \begin{align} (1+u^{2})^{2m} \phi(\alpha_1^{2m}) &= \sum_{s=0}^{m} \binom{2m}{2s} (1-u^{2})^{2s} (2u)^{2m-2s} \phi(\alpha_1^{2s} \alpha_2^{2m-2s}) \notag \\ & \quad + \sum_{s=1}^{m} \binom{2m}{2s-1} (1-u^{2})^{2s-1} (2u)^{2m-2s+1} \phi(\alpha_1^{2s-1} \alpha_2^{2m-2s+1}). \end{align} $$
The two polynomials
![]() $\pi _{1} = \alpha _1^{2s} \alpha _2^{2m-2s} - \alpha _1^{2s} (1-\alpha _1^{2})^{m-s}$
and
$\pi _{1} = \alpha _1^{2s} \alpha _2^{2m-2s} - \alpha _1^{2s} (1-\alpha _1^{2})^{m-s}$
and
![]() $\pi _{2} = \alpha _1^{2s-1}\alpha _2^{2m-2s+1} - \alpha _1^{2s-1} (1-\alpha _1^{2})^{m-s} \alpha _2$
both evaluate to the zero function on
$\pi _{2} = \alpha _1^{2s-1}\alpha _2^{2m-2s+1} - \alpha _1^{2s-1} (1-\alpha _1^{2})^{m-s} \alpha _2$
both evaluate to the zero function on
![]() $S^1$
so by Locality,
$S^1$
so by Locality,
 $$ \begin{align} \kern2pt\phi(\alpha_1^{2s}\alpha_2^{2m-2s}) &= \phi(\alpha_1^{2s}(1-\alpha_1^{2})^{m-s}) = \sum_{t=0}^{m-s} (-1)^{t} \binom{m-s}{t} \phi(\alpha_1^{2s+2t}),\qquad\ \end{align} $$
$$ \begin{align} \kern2pt\phi(\alpha_1^{2s}\alpha_2^{2m-2s}) &= \phi(\alpha_1^{2s}(1-\alpha_1^{2})^{m-s}) = \sum_{t=0}^{m-s} (-1)^{t} \binom{m-s}{t} \phi(\alpha_1^{2s+2t}),\qquad\ \end{align} $$
 $$ \begin{align} \phi(\alpha_1^{2s-1} \alpha_2^{2m-2s+1}) &= \phi(\alpha_1^{2s-1} (1 - \alpha_1^{2})^{m-s}\alpha_2) = \sum_{t=0}^{m-s} (-1)^{t} \binom{m-s}{t} \phi(\alpha_1^{2s+2t-1}\alpha_2), \end{align} $$
$$ \begin{align} \phi(\alpha_1^{2s-1} \alpha_2^{2m-2s+1}) &= \phi(\alpha_1^{2s-1} (1 - \alpha_1^{2})^{m-s}\alpha_2) = \sum_{t=0}^{m-s} (-1)^{t} \binom{m-s}{t} \phi(\alpha_1^{2s+2t-1}\alpha_2), \end{align} $$
respectively. By (3.4) and (3.5), (3.3) becomes
 $$ \begin{align*} &(1+u^{2})^{2m} \phi(\alpha_1^{2m}) \\ &\quad = \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s} \binom{m-s}{t} (1-u^{2})^{2s} (2u)^{2m-2s} \phi(\alpha_1^{2s+2t}) \\ &\qquad + \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s-1} \binom{m-s}{t} (1-u^{2})^{2s-1} (2u)^{2m-2s+1} \phi(\alpha_1^{2s+2t-1}\alpha_2). \end{align*} $$
$$ \begin{align*} &(1+u^{2})^{2m} \phi(\alpha_1^{2m}) \\ &\quad = \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s} \binom{m-s}{t} (1-u^{2})^{2s} (2u)^{2m-2s} \phi(\alpha_1^{2s+2t}) \\ &\qquad + \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s-1} \binom{m-s}{t} (1-u^{2})^{2s-1} (2u)^{2m-2s+1} \phi(\alpha_1^{2s+2t-1}\alpha_2). \end{align*} $$
Now the following polynomial of degree at most
![]() $4m$
in
$4m$
in
![]() $\mathbb {F}[\beta ]$
, namely
$\mathbb {F}[\beta ]$
, namely
 $$ \begin{align*} \pi &= (1+\beta^{2})^{2m} \phi(\alpha_1^{2m}) - \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s} \binom{m-s}{t} (1-\beta ^{2})^{2s} (2\beta)^{2m-2s} \phi(\alpha_1^{2s+2t}) \\ &\quad - \sum_{s=0}^{m}\sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s-1} \binom{m-s}{t} (1-\beta^{2})^{2s-1} (2\beta)^{2m-2s+1} \phi(\alpha_1^{2s+2t-1}\alpha_2), \end{align*} $$
$$ \begin{align*} \pi &= (1+\beta^{2})^{2m} \phi(\alpha_1^{2m}) - \sum_{s=0}^{m} \sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s} \binom{m-s}{t} (1-\beta ^{2})^{2s} (2\beta)^{2m-2s} \phi(\alpha_1^{2s+2t}) \\ &\quad - \sum_{s=0}^{m}\sum_{t=0}^{m-s} (-1)^{t} \binom{2m}{2s-1} \binom{m-s}{t} (1-\beta^{2})^{2s-1} (2\beta)^{2m-2s+1} \phi(\alpha_1^{2s+2t-1}\alpha_2), \end{align*} $$
has infinitely many roots, so
![]() $\pi $
is identically zero. By extracting the coefficient of
$\pi $
is identically zero. By extracting the coefficient of
![]() $\beta $
and
$\beta $
and
![]() $\beta ^2$
, respectively we get
$\beta ^2$
, respectively we get
![]() $4m\phi (\alpha _1^{2m-1}\alpha _2) = 0$
and
$4m\phi (\alpha _1^{2m-1}\alpha _2) = 0$
and
![]() $8m^{2}\phi (\alpha _1^{2m}) - 4m(2m-1) \phi (\alpha _1^{2m-2}) = 0$
.
$8m^{2}\phi (\alpha _1^{2m}) - 4m(2m-1) \phi (\alpha _1^{2m-2}) = 0$
.
Since m is arbitrary, for any
![]() $m \ge 1$
, we must have
$m \ge 1$
, we must have
![]() $\phi (\alpha _1^{2m-1} \alpha _2) = 0$
and the first-order recurrence relation
$\phi (\alpha _1^{2m-1} \alpha _2) = 0$
and the first-order recurrence relation
![]() $2m \phi (\alpha _1^{2m}) = (2m-1) \phi (\alpha _1^{2m-2})$
with the initial condition
$2m \phi (\alpha _1^{2m}) = (2m-1) \phi (\alpha _1^{2m-2})$
with the initial condition
![]() $\phi (\mathbf {1}) = 1_{\mathbb {F}}$
. Thus, we see that
$\phi (\mathbf {1}) = 1_{\mathbb {F}}$
. Thus, we see that
![]() $\phi (\alpha _1^{2m})$
and
$\phi (\alpha _1^{2m})$
and
![]() $\phi (\alpha _1^{2m-1}\alpha _2)$
are uniquely determined for all
$\phi (\alpha _1^{2m-1}\alpha _2)$
are uniquely determined for all
![]() $m \ge 1$
.
$m \ge 1$
.
Finally, by using the Locality condition again, both
![]() $\phi (\alpha _1^{2m+1}\alpha _2^{2n+1})$
and
$\phi (\alpha _1^{2m+1}\alpha _2^{2n+1})$
and
![]() $\phi (\alpha _1^{2m}\alpha _2^{2n})$
are uniquely determined since
$\phi (\alpha _1^{2m}\alpha _2^{2n})$
are uniquely determined since
 $$ \begin{align*} \phi(\alpha_1^{2m+1}\alpha_2^{2n+1}) &= \phi(\alpha_1^{2m+1}(1-\alpha_1^{2})^{n}\alpha_2 ) = \sum_{s=0}^{n} (-1)^{n} \binom{n}{s} \phi(\alpha_1^{2m+2s+1}\alpha_2), \\ \phi(\alpha_1^{2m}\alpha_2^{2n}) &= \phi(\alpha_1^{2m} (1-\alpha_1^{2})^{n} ) = \sum_{s=0}^{n} (-1)^{n} \binom{n}{s} \phi(\alpha_1^{2m+2s}). \end{align*} $$
$$ \begin{align*} \phi(\alpha_1^{2m+1}\alpha_2^{2n+1}) &= \phi(\alpha_1^{2m+1}(1-\alpha_1^{2})^{n}\alpha_2 ) = \sum_{s=0}^{n} (-1)^{n} \binom{n}{s} \phi(\alpha_1^{2m+2s+1}\alpha_2), \\ \phi(\alpha_1^{2m}\alpha_2^{2n}) &= \phi(\alpha_1^{2m} (1-\alpha_1^{2})^{n} ) = \sum_{s=0}^{n} (-1)^{n} \binom{n}{s} \phi(\alpha_1^{2m+2s}). \end{align*} $$
This concludes the proof.
4 Generalisation to arbitrary circles
Fix a point
![]() $(a,b) \in \mathbb {A}$
and a nonzero
$(a,b) \in \mathbb {A}$
and a nonzero
![]() $r\in \mathbb {F}$
. We define
$r\in \mathbb {F}$
. We define
![]() $S^1_{r,(a,b)}$
to be the collection of points
$S^1_{r,(a,b)}$
to be the collection of points
![]() $(x_1,x_2) \in \mathbb {A}$
such that
$(x_1,x_2) \in \mathbb {A}$
such that
![]() $(x-a)^2 + (y-b)^2 = r^2$
. A linear functional
$(x-a)^2 + (y-b)^2 = r^2$
. A linear functional
![]() $\phi _{r,(a,b)} \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}$
is a circular integral functional on
$\phi _{r,(a,b)} \colon \mathbb {F}[\alpha _1, \alpha _2] \rightarrow \mathbb {F}$
is a circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1_{r,(a,b)}$
if the following conditions are satisfied.
$S^1_{r,(a,b)}$
if the following conditions are satisfied.
-
(Normalisation) For the multiplicative identity
 $\mathbf {1}$
of
$\mathbf {1}$
of
 $\mathbb {F}[\alpha _1, \alpha _2]$
, we have
$\mathbb {F}[\alpha _1, \alpha _2]$
, we have
 $\phi _{r,(a,b)}(\mathbf {1}) = r$
.
$\phi _{r,(a,b)}(\mathbf {1}) = r$
. -
(Locality) If
 $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
such that
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
such that
 $\varepsilon (\pi ) = 0$
on
$\varepsilon (\pi ) = 0$
on
 $S^1_{r,(a,b)}$
, we have
$S^1_{r,(a,b)}$
, we have
 $\phi _{r,(a,b)}(\pi ) = 0$
.
$\phi _{r,(a,b)}(\pi ) = 0$
. -
(Invariance) For any
 $\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
and
$\pi \in \mathbb {F}[\alpha _1, \alpha _2]$
and
 $h \in \mathrm {SO}(2,\mathbb {F})$
,
$h \in \mathrm {SO}(2,\mathbb {F})$
,
 $\phi _{r,(a,b)} (h \cdot \pi ) = \phi _{r,(a,b)}(\pi )$
.
$\phi _{r,(a,b)} (h \cdot \pi ) = \phi _{r,(a,b)}(\pi )$
.
By employing the same analysis, the existence and uniqueness of a circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1_{r,(a,b)}$
can be derived from that of
$S^1_{r,(a,b)}$
can be derived from that of
![]() $\psi $
.
$\psi $
.
Theorem 4.1. There is one and only one circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1_{r,(a,b)}$
, given by
$S^1_{r,(a,b)}$
, given by
where
![]() $\psi $
is the circular integral functional on
$\psi $
is the circular integral functional on
![]() $\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
$\mathbb {F}[\alpha _1, \alpha _2]$
with respect to
![]() $S^1$
.
$S^1$
.
Now we are finally able to give an algebraic interpretation of the super Catalan numbers
![]() $S(m,n)$
.
$S(m,n)$
.
Theorem 4.2 (An algebraic interpretation of
 $S(m,n)$
).
$S(m,n)$
).
Over
![]() $\mathbb {Q}$
, for any
$\mathbb {Q}$
, for any
![]() $m, n \in \mathbb {N}$
, we have
$m, n \in \mathbb {N}$
, we have
![]() $2S(m,n) = \psi _{2,(0,0)}(\alpha _1^{2m} \alpha _2^{2n})$
.
$2S(m,n) = \psi _{2,(0,0)}(\alpha _1^{2m} \alpha _2^{2n})$
.
Proof. The result follows immediately from Theorem 4.1 since
Acknowledgement
The author thanks Hopein Christofen Tang for helpful discussions.