Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T21:13:21.550Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXACT FORMULA FOR THE HARMONIC CONTINUED FRACTION

Part of: Elementary number theory Diophantine approximation, transcendental number theory Computational number theory

Published online by Cambridge University Press:  10 June 2020

MARTIN BUNDER ,
PETER NICKOLAS Open the ORCID record for PETER NICKOLAS [Opens in a new window]  and
JOSEPH TONIEN Open the ORCID record for JOSEPH TONIEN [Opens in a new window]
MARTIN BUNDER
Affiliation:
School of Mathematics and Applied Statistics,University of Wollongong, New South Wales2522, Australia email martin.bunder@uow.edu.au
PETER NICKOLAS
Affiliation:
School of Mathematics and Applied Statistics,University of Wollongong, New South Wales2522, Australia email peter.nickolas@uow.edu.au
JOSEPH TONIEN*
Affiliation:
School of Computing and Information Technology,University of Wollongong, New South Wales2522, Australia email joseph.tonien@uow.edu.au
*
✉joseph.tonien@uow.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

For a positive real number $t$, define the harmonic continued fraction

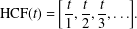$$\begin{eqnarray}\text{HCF}(t)=\biggl[\frac{t}{1},\frac{t}{2},\frac{t}{3},\ldots \biggr].\end{eqnarray}$$
We prove that
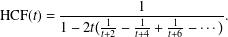$$\begin{eqnarray}\text{HCF}(t)=\frac{1}{1-2t(\frac{1}{t+2}-\frac{1}{t+4}+\frac{1}{t+6}-\cdots \,)}.\end{eqnarray}$$

Keywords

continued fractionharmonic continued fractionSeidel–Stern theorem

MSC classification

Primary: 11A55: Continued fractions
Secondary: 11J70: Continued fractions and generalizations 11Y65: Continued fraction calculations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 11 - 21
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beardon, A. F. and Short, I., ‘The Seidel, Stern, Stolz and Van Vleck theorems on continued fractions’, Bull. Lond. Math. Soc. 42 (2010), 457–466.10.1112/blms/bdq006CrossRefGoogle Scholar
Bunder, M., Nickolas, P. and Tonien, J., ‘On the harmonic continued fractions’, Ramanujan J. 49 (2019), 669–697.CrossRefGoogle Scholar
Bunder, M. and Tonien, J., ‘Closed form expressions for two harmonic continued fractions’, Math. Gaz. 101 (2017), 439–448.CrossRefGoogle Scholar
Euler, L., ‘De fractionibus continuis observationes’, Comment. Acad. Sci. Imp. Petropol. 11 (1750), 32–81.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 6th edn (Oxford University Press, Oxford, 2008).Google Scholar
Lorentzen, L. and Waadeland, H., Continued Fractions with Applications, Studies in Computational Mathematics, 3 (North-Holland, Amsterdam, 1992).Google Scholar
Seidel, L., Untersuchungen über die Konvergenz und Divergenz der Kettenbrüche, Habilschrift, München, 1846.Google Scholar
Stern, M. A., ‘Über die Kennzeichen der Konvergenz eines Kettenbruchs’, J. reine angew. Math. 37 (1848), 255–272.Google Scholar