No CrossRef data available.
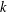 $k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
$k$-HESSIAN IN FRACTIONAL SOBOLEV SPACESPublished online by Cambridge University Press: 23 October 2019
We introduce the notion of a distributional 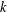 $k$-Hessian (
$k$-Hessian (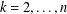 $k=2,\ldots ,n$) associated with fractional Sobolev functions on
$k=2,\ldots ,n$) associated with fractional Sobolev functions on  $\unicode[STIX]{x1D6FA}$, a smooth bounded open subset in
$\unicode[STIX]{x1D6FA}$, a smooth bounded open subset in 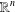 $\mathbb{R}^{n}$. We show that the distributional
$\mathbb{R}^{n}$. We show that the distributional 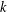 $k$-Hessian is weakly continuous on the fractional Sobolev space
$k$-Hessian is weakly continuous on the fractional Sobolev space 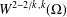 $W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$ and that the weak continuity result is optimal, that is, the distributional
$W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$ and that the weak continuity result is optimal, that is, the distributional 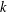 $k$-Hessian is well defined in
$k$-Hessian is well defined in 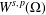 $W^{s,p}(\unicode[STIX]{x1D6FA})$ if and only if
$W^{s,p}(\unicode[STIX]{x1D6FA})$ if and only if 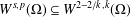 $W^{s,p}(\unicode[STIX]{x1D6FA})\subseteq W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$.
$W^{s,p}(\unicode[STIX]{x1D6FA})\subseteq W^{2-2/k,k}(\unicode[STIX]{x1D6FA})$.
This work is supported by Hubei Key Laboratory of Applied Mathematics, Hubei University.