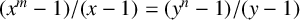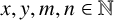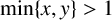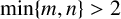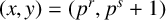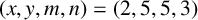1 Introduction
Let
![]() ${\mathbb {N}}$
be the set of all positive integers. One hundred years ago, Ratat [Reference Ratat27] and Rose and Goormaghtigh [Reference Rose and Goormaghtigh28] conjectured that the equation
${\mathbb {N}}$
be the set of all positive integers. One hundred years ago, Ratat [Reference Ratat27] and Rose and Goormaghtigh [Reference Rose and Goormaghtigh28] conjectured that the equation
 $$ \begin{align} \frac{x^m-1}{x-1}=\frac{y^n-1}{y-1} \quad \mbox{for all } x,y,m,n \in {\mathbb{N}}, x \ne y, \min\{x,y\}>1, \min\{m,n\}>2, \end{align} $$
$$ \begin{align} \frac{x^m-1}{x-1}=\frac{y^n-1}{y-1} \quad \mbox{for all } x,y,m,n \in {\mathbb{N}}, x \ne y, \min\{x,y\}>1, \min\{m,n\}>2, \end{align} $$
has only two solutions
![]() $(x,y,m,n)=(2,5,5,3)$
and
$(x,y,m,n)=(2,5,5,3)$
and
![]() $(2,90,13,3)$
with
$(2,90,13,3)$
with
![]() $x<y$
. Equation (1.1) is usually called the Goormaghtigh equation. The above conjecture is a very difficult problem in Diophantine equations. It was solved for some special cases (see [Reference Balasubramanian and Shorey3, Reference Bennett, Garbuz and Marten5, Reference Bennett, Gherga and Kreso6, Reference Bugeaud and Shorey9, Reference Davenport, Lewis and Schinzel10, Reference He12, Reference Karanikolov14–Reference Le18, Reference Makowski and Schinzel22, Reference Makowski and Schinzel23, Reference Nesterenko and Shorey26, Reference Saradha29–Reference Yuan37]). But, in general, the problem is far from solved. The solution of (1.1) is closely related to some problems in number theory, combinatorics and algebra (see [Reference Abdollahi and Mohammadi Hassanabadi1, Reference Bateman and Stemmler4, Reference He and Togbé13, Reference Leung, Ma and Schmidt19, Reference Luca21]). For example, while discussing the partial geometries admitting Singer groups in combinatorics, Leung et al. [Reference Leung, Ma and Schmidt19] found that the existence of partial difference sets in an elementary abelian
$x<y$
. Equation (1.1) is usually called the Goormaghtigh equation. The above conjecture is a very difficult problem in Diophantine equations. It was solved for some special cases (see [Reference Balasubramanian and Shorey3, Reference Bennett, Garbuz and Marten5, Reference Bennett, Gherga and Kreso6, Reference Bugeaud and Shorey9, Reference Davenport, Lewis and Schinzel10, Reference He12, Reference Karanikolov14–Reference Le18, Reference Makowski and Schinzel22, Reference Makowski and Schinzel23, Reference Nesterenko and Shorey26, Reference Saradha29–Reference Yuan37]). But, in general, the problem is far from solved. The solution of (1.1) is closely related to some problems in number theory, combinatorics and algebra (see [Reference Abdollahi and Mohammadi Hassanabadi1, Reference Bateman and Stemmler4, Reference He and Togbé13, Reference Leung, Ma and Schmidt19, Reference Luca21]). For example, while discussing the partial geometries admitting Singer groups in combinatorics, Leung et al. [Reference Leung, Ma and Schmidt19] found that the existence of partial difference sets in an elementary abelian
![]() $3$
-group is related to the solutions
$3$
-group is related to the solutions
![]() $(x,y,m,n)$
of (1.1) with
$(x,y,m,n)$
of (1.1) with
where r is a positive integer. In [Reference Leung, Ma and Schmidt19], they proved that (1.1) has no solutions
![]() $(x,y,m,n)$
satisfying (1.2).
$(x,y,m,n)$
satisfying (1.2).
Let p be a prime and let r, s be positive integers. In this paper, we discuss the solutions
![]() $(x,y,m,n)$
of (1.1) with
$(x,y,m,n)$
of (1.1) with
Thus, we generalise the above-mentioned result in [Reference Leung, Ma and Schmidt19] to prove the following theorem.
Combining Theorem 1.1 and [Reference Leung, Ma and Schmidt19, Corollary 37] with
![]() $q=\alpha +1=2^s+1$
, we immediately obtain the following corollary which may be regarded as a generalisation of [Reference Leung, Ma and Schmidt19, Corollary 44].
$q=\alpha +1=2^s+1$
, we immediately obtain the following corollary which may be regarded as a generalisation of [Reference Leung, Ma and Schmidt19, Corollary 44].
Corollary 1.2. Suppose that a proper partial geometry
![]() $\varPi $
has at least two subgroup lines and that the parameters of the corresponding partial difference set have the form in [Reference Leung, Ma and Schmidt19, (34)]. Then,
$\varPi $
has at least two subgroup lines and that the parameters of the corresponding partial difference set have the form in [Reference Leung, Ma and Schmidt19, (34)]. Then,
![]() $\varPi $
cannot be expressed as
$\varPi $
cannot be expressed as
with
![]() $r,s,t \in {\mathbb {N}}$
.
$r,s,t \in {\mathbb {N}}$
.
The organisation of the paper is as follows. In Section 2, we prove Theorem 1.1 in the case where
![]() $r \le s$
using an upper bound for the number of solutions of the generalised Ramanujan–Nagell equations due to Bugeaud and Shorey [Reference Bugeaud and Shorey8]. In Section 3, using a lower bound for linear forms in three logarithms due to Matveev [Reference Matveev24], we show that if
$r \le s$
using an upper bound for the number of solutions of the generalised Ramanujan–Nagell equations due to Bugeaud and Shorey [Reference Bugeaud and Shorey8]. In Section 3, using a lower bound for linear forms in three logarithms due to Matveev [Reference Matveev24], we show that if
![]() $r>s$
and
$r>s$
and
![]() $p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
$p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
![]() $(x,y,m,n)$
with (1.3). Thus, the remaining case to be checked is
$(x,y,m,n)$
with (1.3). Thus, the remaining case to be checked is
![]() $r>s$
and
$r>s$
and
![]() $p^r<3.436\times 10^{15}$
. For this, we appeal to the reduction method due to Dujella and Pethő [Reference Dujella and Pethő11], based on [Reference Baker and Davenport2, Lemma] by Baker and Davenport, to complete the proof of Theorem 1.1 in Section 4.
$p^r<3.436\times 10^{15}$
. For this, we appeal to the reduction method due to Dujella and Pethő [Reference Dujella and Pethő11], based on [Reference Baker and Davenport2, Lemma] by Baker and Davenport, to complete the proof of Theorem 1.1 in Section 4.
2 The case
 $r \le s$
$r \le s$
Lemma 2.1 [Reference Ljunggren20]
The equation
has only two solutions,
![]() $(X,Y,k,l)=(3,11,5,2)$
and
$(X,Y,k,l)=(3,11,5,2)$
and
![]() $(7,20,4,2)$
with
$(7,20,4,2)$
with
![]() $2 \mid l$
.
$2 \mid l$
.
Let
![]() $D_1$
and
$D_1$
and
![]() $D_2$
be coprime positive integers and let p be a prime with
$D_2$
be coprime positive integers and let p be a prime with
![]() $p \nmid D_1D_2$
. Further, let
$p \nmid D_1D_2$
. Further, let
![]() $N(D_1,D_2,p)$
denote the number of solutions
$N(D_1,D_2,p)$
denote the number of solutions
![]() $(X,Z)$
of the equation
$(X,Z)$
of the equation
Combining the results in [Reference Bugeaud, Mignotte and Siksek7, Reference Bugeaud and Shorey8], we immediately obtain the following two lemmas.
Lemma 2.2. We have
![]() $N(D_1,D_2,2) \le 1$
, except for the following cases:
$N(D_1,D_2,2) \le 1$
, except for the following cases:
-
(i)
 $N(1,7,2)=5$
,
$N(1,7,2)=5$
,
 $(X,Z)=(1,3),(3,4),(5,5),(11,7)$
and
$(X,Z)=(1,3),(3,4),(5,5),(11,7)$
and
 $(181,15)$
;
$(181,15)$
; -
(ii)
 $N(3,5,2)=3$
,
$N(3,5,2)=3$
,
 $(X,Z)=(1,3),(3,5)$
and
$(X,Z)=(1,3),(3,5)$
and
 $(13,9)$
;
$(13,9)$
; -
(iii)
 $N(7,1,2)=2$
,
$N(7,1,2)=2$
,
 $(X,Z)=(1,3)$
and
$(X,Z)=(1,3)$
and
 $(3,6)$
;
$(3,6)$
; -
(iv)
 $N(1,2^{k+2}-1,2)=2$
,
$N(1,2^{k+2}-1,2)=2$
,
 $(X,Z)=(1,k+2)$
and
$(X,Z)=(1,k+2)$
and
 $(2^{k+1}-1,2k+2)$
, where k is a positive integer with
$(2^{k+1}-1,2k+2)$
, where k is a positive integer with
 $k>1$
;
$k>1$
; -
(v)
 $N(3,29,2)=2$
,
$N(3,29,2)=2$
,
 $(X,Z)=(1,5)$
and
$(X,Z)=(1,5)$
and
 $(209,17)$
;
$(209,17)$
; -
(vi)
 $N(5,3,2)=2$
,
$N(5,3,2)=2$
,
 $(X,Z)=(1,3)$
and
$(X,Z)=(1,3)$
and
 $(5,7)$
;
$(5,7)$
; -
(vii)
 $N(13,3,2)=2$
,
$N(13,3,2)=2$
,
 $(X,Z)=(1,4)$
and
$(X,Z)=(1,4)$
and
 $(71,16)$
;
$(71,16)$
; -
(viii)
 $N(21,11,2)=2$
,
$N(21,11,2)=2$
,
 $(X,Z)=(1,5)$
and
$(X,Z)=(1,5)$
and
 $(79,17)$
; and
$(79,17)$
; and -
(ix) if
 $D_1a^2{\kern-1pt}={\kern-1pt}2^k{\kern-1pt}-{\kern-1pt}\delta $
and
$D_1a^2{\kern-1pt}={\kern-1pt}2^k{\kern-1pt}-{\kern-1pt}\delta $
and
 $D_2=3\cdot 2^k{\kern-1pt}+{\kern-1pt}\delta $
, where a, k are positive integers with
$D_2=3\cdot 2^k{\kern-1pt}+{\kern-1pt}\delta $
, where a, k are positive integers with
 $k{\kern-1pt}>{\kern-1pt}1$
and
$k{\kern-1pt}>{\kern-1pt}1$
and
 $\delta \in \{1,-1\}$
, then
$\delta \in \{1,-1\}$
, then
 $N(D_1,D_2,2)=2$
,
$N(D_1,D_2,2)=2$
,
 $(X,Z)=(a,k+2)$
and
$(X,Z)=(a,k+2)$
and
 $((2^{k+1}+\delta )a, 3k+2)$
.
$((2^{k+1}+\delta )a, 3k+2)$
.
Lemma 2.3. If
![]() $p \ne 2$
, then
$p \ne 2$
, then
![]() $N(D_1,D_2,p)\le 1$
, except for the following cases:
$N(D_1,D_2,p)\le 1$
, except for the following cases:
-
(i)
 $N(2,1,3)=3$
,
$N(2,1,3)=3$
,
 $(X,Z)=(1,1), (2,2)$
and
$(X,Z)=(1,1), (2,2)$
and
 $(11,5)$
; and
$(11,5)$
; and -
(ii) if
 $4D_1a^2=p^k-\delta $
and
$4D_1a^2=p^k-\delta $
and
 $4D_2=3p^k+\delta $
, where a, k are positive integers and
$4D_2=3p^k+\delta $
, where a, k are positive integers and
 $\delta \in \{1,-1\}$
, then
$\delta \in \{1,-1\}$
, then
 $N(D_1,D_2,p)=2$
,
$N(D_1,D_2,p)=2$
,
 $(X,Z)=(a,k)$
and
$(X,Z)=(a,k)$
and
 $((2p^k+\delta )a,3k)$
.
$((2p^k+\delta )a,3k)$
.
Proof. We now assume that
![]() $(x,y,m,n)$
is a solution of (1.1) with (1.3). Then
$(x,y,m,n)$
is a solution of (1.1) with (1.3). Then
 $$ \begin{align} \frac{p^{rm}-1}{p^r-1}=\frac{(p^s+1)^n-1}{p^s}. \end{align} $$
$$ \begin{align} \frac{p^{rm}-1}{p^r-1}=\frac{(p^s+1)^n-1}{p^s}. \end{align} $$
When
![]() $r=s$
, by (2.3),
$r=s$
, by (2.3),
 $$ \begin{align} \frac{p^{r(m+1)}-1}{p^r-1}=(p^r+1)^n. \end{align} $$
$$ \begin{align} \frac{p^{r(m+1)}-1}{p^r-1}=(p^r+1)^n. \end{align} $$
If
![]() $2 \mid n$
, by (2.4), the equation (2.1) has a solution
$2 \mid n$
, by (2.4), the equation (2.1) has a solution
![]() $(X,Y,k,l)=(p^r,p^r+1,m+1,n)$
with
$(X,Y,k,l)=(p^r,p^r+1,m+1,n)$
with
![]() $2 \mid l$
. However, since
$2 \mid l$
. However, since
![]() $m>2$
, by Lemma 2.1, this is impossible. So
$m>2$
, by Lemma 2.1, this is impossible. So
![]() $2 \nmid n$
and
$2 \nmid n$
and
![]() $n \ge 3$
.
$n \ge 3$
.
Since
![]() $p^r+1>2$
and
$p^r+1>2$
and
![]() $p^r \equiv -1 \pmod {(p^r+1)}$
, by (2.4),
$p^r \equiv -1 \pmod {(p^r+1)}$
, by (2.4),
from which we get
![]() $2 \mid m+1$
. Hence, by (2.4),
$2 \mid m+1$
. Hence, by (2.4),
 $$ \begin{align} \frac{(p^{2r})^{(m+1)/2}-1}{p^{2r}-1}=(p^r+1)^{n-1}. \end{align} $$
$$ \begin{align} \frac{(p^{2r})^{(m+1)/2}-1}{p^{2r}-1}=(p^r+1)^{n-1}. \end{align} $$
Recall that
![]() $2 \nmid n$
and
$2 \nmid n$
and
![]() $n \ge 3$
. We see from (2.5) that if
$n \ge 3$
. We see from (2.5) that if
![]() $(m+1)/2>2$
, then (2.1) has a solution
$(m+1)/2>2$
, then (2.1) has a solution
![]() $(X,Y,k,l)=(p^{2r},p^r+1,(m+1)/2,n-1)$
with
$(X,Y,k,l)=(p^{2r},p^r+1,(m+1)/2,n-1)$
with
![]() $2 \mid l$
. But, by Lemma 2.1 again, this is impossible. Therefore, since
$2 \mid l$
. But, by Lemma 2.1 again, this is impossible. Therefore, since
![]() $2 \nmid m$
and
$2 \nmid m$
and
![]() $m \ge 3$
, we get
$m \ge 3$
, we get
![]() $m=3$
, and by (2.5),
$m=3$
, and by (2.5),
 $$ \begin{align*} \frac{(p^{2r})^{(m+1)/2}-1}{p^{2r}-1}=\frac{p^{4r}-1}{p^{2r}-1}=p^{2r}+1=(p^r+1)^{n-1} \ge (p^r+1)^2>p^{2r}+1, \end{align*} $$
$$ \begin{align*} \frac{(p^{2r})^{(m+1)/2}-1}{p^{2r}-1}=\frac{p^{4r}-1}{p^{2r}-1}=p^{2r}+1=(p^r+1)^{n-1} \ge (p^r+1)^2>p^{2r}+1, \end{align*} $$
which is a contradiction. Thus, (1.1) has no solutions
![]() $(x,y,m,n)$
with (1.3) and
$(x,y,m,n)$
with (1.3) and
![]() $r=s$
.
$r=s$
.
When
![]() $r<s$
, by (2.3),
$r<s$
, by (2.3),
Since
![]() $r<s$
,
$r<s$
,
![]() $p^r-1$
,
$p^r-1$
,
![]() $p^s+1$
and
$p^s+1$
and
![]() $p^s-p^r+1$
are positive integers satisfying
$p^s-p^r+1$
are positive integers satisfying
If
![]() $2 \mid n$
, by (2.6), the equation (2.2) has a solution
$2 \mid n$
, by (2.6), the equation (2.2) has a solution
for
![]() $(D_1,D_2)=(p^r-1,p^s-p^r+1)$
. Notice that (2.2) has another solution
$(D_1,D_2)=(p^r-1,p^s-p^r+1)$
. Notice that (2.2) has another solution
![]() $(X,Z)=(1,s)$
for
$(X,Z)=(1,s)$
for
![]() $(D_1,D_2)=(p^r-1,p^s-p^r+1)$
. So
$(D_1,D_2)=(p^r-1,p^s-p^r+1)$
. So
However, by (2.7), using Lemmas 2.2 and 2.3, (2.8) is false.
Similarly, if
![]() $2 \nmid n$
, by (2.6), the equation (2.2) has a solution
$2 \nmid n$
, by (2.6), the equation (2.2) has a solution
for
![]() $(D_1,D_2)=((p^r-1)(p^s+1),p^s-p^r+1)$
. Moreover, (2.2) has another solution
$(D_1,D_2)=((p^r-1)(p^s+1),p^s-p^r+1)$
. Moreover, (2.2) has another solution
![]() $(X,Z)=(1,r+s)$
for
$(X,Z)=(1,r+s)$
for
![]() $(D_1,D_2)=((p^r-1)(p^s+1),p^s-p^r+1)$
. So
$(D_1,D_2)=((p^r-1)(p^s+1),p^s-p^r+1)$
. So
Applying Lemmas 2.2 and 2.3 to (2.9), we can only obtain
Therefore, by (1.3) and (2.10), we get
![]() $(D_1,D_2)=(5,3)$
and
$(D_1,D_2)=(5,3)$
and
![]() $(x,y,m,n)=(2,5,5,3)$
. Thus, the proposition is proved.
$(x,y,m,n)=(2,5,5,3)$
. Thus, the proposition is proved.
3 The case
 $r>s$
$r>s$
In this section, we assume that
![]() $r>s$
and
$r>s$
and
![]() $(x,y,m,n)$
is a solution of (1.1) with (1.3).
$(x,y,m,n)$
is a solution of (1.1) with (1.3).
Lemma 3.1. If
![]() $(p,s)\ne (2,1)$
, then
$(p,s)\ne (2,1)$
, then
![]() $n> p^r$
.
$n> p^r$
.
Proof. By (2.3),
 $$ \begin{align*} \frac{p^{rm}-1}{p^r-1}=\sum_{i=0}^{m-1}p^{ri}=\sum_{j=1}^n \binom{n}{j}p^{s(j-1)}=\frac{(p^s+1)^n-1}{p^s}, \end{align*} $$
$$ \begin{align*} \frac{p^{rm}-1}{p^r-1}=\sum_{i=0}^{m-1}p^{ri}=\sum_{j=1}^n \binom{n}{j}p^{s(j-1)}=\frac{(p^s+1)^n-1}{p^s}, \end{align*} $$
from which we get
 $$ \begin{align} p^r\bigg(\frac{p^{r(m-1)}-1}{p^r-1}\bigg)=(n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
$$ \begin{align} p^r\bigg(\frac{p^{r(m-1)}-1}{p^r-1}\bigg)=(n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
Since
![]() $n>2$
and
$n>2$
and
![]() $p \nmid (p^{r(m-1)}-1)/(p^r-1)$
, we see from (3.1) that
$p \nmid (p^{r(m-1)}-1)/(p^r-1)$
, we see from (3.1) that
![]() $p \mid n-1$
and
$p \mid n-1$
and
 $$ \begin{align} p^r\, \|\, (n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
$$ \begin{align} p^r\, \|\, (n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
Let
and
where t is a positive integer and
![]() $t_j\ (j=2,\ldots ,n)$
are nonnegative integers. Then
$t_j\ (j=2,\ldots ,n)$
are nonnegative integers. Then
 $$ \begin{align} t_j \le \frac{\log j}{\log p}\le j-1 \quad \mbox{for all } j=2,\ldots,n. \end{align} $$
$$ \begin{align} t_j \le \frac{\log j}{\log p}\le j-1 \quad \mbox{for all } j=2,\ldots,n. \end{align} $$
Notice that both symbols ‘
![]() $\le $
’ in (3.5) can be taken by equal signs ‘
$\le $
’ in (3.5) can be taken by equal signs ‘
![]() $=$
’ if and only if
$=$
’ if and only if
![]() $(p,t_j,j)=(2,1,2)$
. It follows from (3.5) that if
$(p,t_j,j)=(2,1,2)$
. It follows from (3.5) that if
![]() $(p,t_j)\ne (2,1)$
, then
$(p,t_j)\ne (2,1)$
, then
Hence, since
![]() $\gcd (j,j-1)=1$
and
$\gcd (j,j-1)=1$
and
![]() $(p,s)\ne (2,1)$
, by (3.3), (3.4) and (3.6),
$(p,s)\ne (2,1)$
, by (3.3), (3.4) and (3.6),
 $$ \begin{align} \binom{n}{j}p^{s(j-1)}\equiv n(n-1)\binom{n-2}{j-2}\frac{p^{s(j-1)}}{(j-1)j}\equiv 0 \pmod{p^{t+1}} \quad \mbox{for all } j=2,\ldots,n. \end{align} $$
$$ \begin{align} \binom{n}{j}p^{s(j-1)}\equiv n(n-1)\binom{n-2}{j-2}\frac{p^{s(j-1)}}{(j-1)j}\equiv 0 \pmod{p^{t+1}} \quad \mbox{for all } j=2,\ldots,n. \end{align} $$
Therefore, by (3.3) and (3.7),
 $$ \begin{align} p^t\,\|\,(n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
$$ \begin{align} p^t\,\|\,(n-1)+\sum_{j=2}^n\binom{n}{j}p^{s(j-1)}. \end{align} $$
Further, since
![]() $n>1$
, by (3.3) and (3.9), we obtain
$n>1$
, by (3.3) and (3.9), we obtain
![]() $n-1 \ge p^r$
and
$n-1 \ge p^r$
and
![]() $n>p^r$
. The lemma is proved.
$n>p^r$
. The lemma is proved.
Let
![]() ${\mathbb {Z}}$
,
${\mathbb {Z}}$
,
![]() ${\mathbb {Q}}$
and
${\mathbb {Q}}$
and
![]() ${\mathbb {R}}$
be the sets of all integers, rational numbers and real numbers, respectively. Let
${\mathbb {R}}$
be the sets of all integers, rational numbers and real numbers, respectively. Let
![]() $\alpha $
be an algebraic number of degree d and let
$\alpha $
be an algebraic number of degree d and let
![]() $\alpha ^{(1)},\ldots ,\alpha ^{(d)}$
denote all the conjugates of
$\alpha ^{(1)},\ldots ,\alpha ^{(d)}$
denote all the conjugates of
![]() $\alpha $
. Further, let
$\alpha $
. Further, let
 $$ \begin{align*} f(X)=a\prod_{i=1}^d(X-\alpha^{(i)})\in {\mathbb{Z}}[X] \quad \mbox{for all } a \in {\mathbb{N}} \end{align*} $$
$$ \begin{align*} f(X)=a\prod_{i=1}^d(X-\alpha^{(i)})\in {\mathbb{Z}}[X] \quad \mbox{for all } a \in {\mathbb{N}} \end{align*} $$
denote the minimal polynomial of
![]() $\alpha $
. Then
$\alpha $
. Then
 $$ \begin{align*} \mathop{\mathrm{h}}\nolimits(\alpha)=\frac{1}{d}\bigg(\log a +\sum_{i=1}^d\log \max\{1,|\alpha^{(i)}|\}\bigg) \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{h}}\nolimits(\alpha)=\frac{1}{d}\bigg(\log a +\sum_{i=1}^d\log \max\{1,|\alpha^{(i)}|\}\bigg) \end{align*} $$
is called the absolute logarithmic height of
![]() $\alpha $
.
$\alpha $
.
Lemma 3.2 ([Reference Matveev24, Reference Mignotte and Voutier25])
Let
![]() $\alpha _1$
,
$\alpha _1$
,
![]() $\alpha _2$
,
$\alpha _2$
,
![]() $\alpha _3$
be three distinct real algebraic numbers with
$\alpha _3$
be three distinct real algebraic numbers with
![]() $\min \{\alpha _1,\alpha _2,\alpha _3\}>1$
and let
$\min \{\alpha _1,\alpha _2,\alpha _3\}>1$
and let
![]() $b_1$
,
$b_1$
,
![]() $b_2$
,
$b_2$
,
![]() $b_3$
be three positive integers with
$b_3$
be three positive integers with
![]() $\gcd (b_1,b_2,b_3)=1$
. Further, let
$\gcd (b_1,b_2,b_3)=1$
. Further, let
If
![]() $\varLambda \ne 0$
, then
$\varLambda \ne 0$
, then
where
Proposition 3.3. If
![]() $r>s$
and
$r>s$
and
![]() $p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
$p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
![]() $(x,y,m,n)$
with (1.3).
$(x,y,m,n)$
with (1.3).
Proof. By [Reference Leung, Ma and Schmidt19], the proposition holds for
![]() $(p,s)=(2,1)$
. We can therefore assume that
$(p,s)=(2,1)$
. We can therefore assume that
![]() $(p,s)\ne (2,1)$
. By (2.3),
$(p,s)\ne (2,1)$
. By (2.3),
Since
![]() $p^r-p^s-1>0$
, taking the logarithms of both sides of (3.14),
$p^r-p^s-1>0$
, taking the logarithms of both sides of (3.14),
 $$ \begin{align} \log(p^r-1)+n\log(p^s+1)=(rm+s)\log p+\log \bigg(1+\frac{p^r-p^s-1}{p^{rm+s}}\bigg). \end{align} $$
$$ \begin{align} \log(p^r-1)+n\log(p^s+1)=(rm+s)\log p+\log \bigg(1+\frac{p^r-p^s-1}{p^{rm+s}}\bigg). \end{align} $$
Since
![]() $\log (1+\varepsilon )<\varepsilon $
for any
$\log (1+\varepsilon )<\varepsilon $
for any
![]() $\varepsilon>0$
, by (3.15),
$\varepsilon>0$
, by (3.15),
 $$ \begin{align} \begin{array}{ll} &0 <\log(p^r-1)+n\log(p^s+1)-(rm+s)\log p\\[6pt] &\quad =\log \bigg(1+\dfrac{p^r-p^s-1}{p^{rm+s}}\bigg)<\dfrac{p^r-p^s-1}{p^{rm+s}}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} &0 <\log(p^r-1)+n\log(p^s+1)-(rm+s)\log p\\[6pt] &\quad =\log \bigg(1+\dfrac{p^r-p^s-1}{p^{rm+s}}\bigg)<\dfrac{p^r-p^s-1}{p^{rm+s}}. \end{array} \end{align} $$
Take
and
By (3.16) and (3.18), we have
![]() $\varLambda>0$
and
$\varLambda>0$
and
In order to apply Lemma 3.2, by (3.10), (3.11) and (3.17), we can choose the following parameters.
Further, by (3.12), (3.13), (3.16), (3.20) and (3.21),
 $$ \begin{align*} B=\frac{(rm+s)\log p}{\log(p^r-1)} \end{align*} $$
$$ \begin{align*} B=\frac{(rm+s)\log p}{\log(p^r-1)} \end{align*} $$
and
Applying Lemma 3.2 to (3.17) and (3.18), by (3.20)–(3.22),
 $$ \begin{align} \log \varLambda&>-1.691\times 10^{10}(\log(p^r-1))(\log(p^s+1))(\log p)\nonumber\\ &\quad\times \bigg(1.406+\log \bigg(\dfrac{(rm+s)\log p}{\log(p^r-1)}\bigg)\bigg). \end{align} $$
$$ \begin{align} \log \varLambda&>-1.691\times 10^{10}(\log(p^r-1))(\log(p^s+1))(\log p)\nonumber\\ &\quad\times \bigg(1.406+\log \bigg(\dfrac{(rm+s)\log p}{\log(p^r-1)}\bigg)\bigg). \end{align} $$
Substituting (3.23) into (3.19), we get
 $$ \begin{align} 1+1.691\times 10^{10}(\log(p^s+1))(\log p)\bigg(1.406+\log\bigg(\dfrac{(rm+s)\log p}{\log(p^r-1)}\bigg)\bigg)>\dfrac{(rm+s)\log p}{\log(p^r-1)}. \end{align} $$
$$ \begin{align} 1+1.691\times 10^{10}(\log(p^s+1))(\log p)\bigg(1.406+\log\bigg(\dfrac{(rm+s)\log p}{\log(p^r-1)}\bigg)\bigg)>\dfrac{(rm+s)\log p}{\log(p^r-1)}. \end{align} $$
Hence, since
![]() $(p,s)\ne (2,1)$
and
$(p,s)\ne (2,1)$
and
![]() $p^s+1 \ge 4$
, by (3.23), we can calculate that
$p^s+1 \ge 4$
, by (3.23), we can calculate that
 $$ \begin{align} \frac{(rm+s)\log p}{\log(p^r-1)}<1.501\times 10^{12}(\log(p^s+1))(\log p)(\log \log(p^s+1)). \end{align} $$
$$ \begin{align} \frac{(rm+s)\log p}{\log(p^r-1)}<1.501\times 10^{12}(\log(p^s+1))(\log p)(\log \log(p^s+1)). \end{align} $$
On the other hand, by (3.16),
 $$ \begin{align} \dfrac{(rm+s)\log p}{\log(p^r-1)}&>\bigg(1-\dfrac{p^r-p^s-1}{p^{rm+s}\log(p^r-1)}\bigg)+\dfrac{n\log(p^s+1)}{\log(p^r-1)}\nonumber\\ &>\dfrac{n\log(p^s+1)}{\log(p^r-1)}. \end{align} $$
$$ \begin{align} \dfrac{(rm+s)\log p}{\log(p^r-1)}&>\bigg(1-\dfrac{p^r-p^s-1}{p^{rm+s}\log(p^r-1)}\bigg)+\dfrac{n\log(p^s+1)}{\log(p^r-1)}\nonumber\\ &>\dfrac{n\log(p^s+1)}{\log(p^r-1)}. \end{align} $$
Since
![]() $\log p \le (\log p^r)/2$
for
$\log p \le (\log p^r)/2$
for
![]() $r \ge 2$
, the combination of (3.25) and (3.26) yields
$r \ge 2$
, the combination of (3.25) and (3.26) yields
 $$ \begin{align} n&<1.501\times 10^{12}(\log p)(\log(p^r-1))(\log \log(p^s+1))\nonumber\\ &<7.505\times 10^{11}( \log p^r)^2(\log \log p^r). \end{align} $$
$$ \begin{align} n&<1.501\times 10^{12}(\log p)(\log(p^r-1))(\log \log(p^s+1))\nonumber\\ &<7.505\times 10^{11}( \log p^r)^2(\log \log p^r). \end{align} $$
Further, since
![]() $(p,s)\ne (2,1)$
, by Lemma 3.1, we have
$(p,s)\ne (2,1)$
, by Lemma 3.1, we have
![]() $n>p^r$
. Hence, by (3.27),
$n>p^r$
. Hence, by (3.27),
Therefore, by (3.28), we obtain
![]() $p^r<3.436\times 10^{15}$
. Thus, if
$p^r<3.436\times 10^{15}$
. Thus, if
![]() $r>s$
and
$r>s$
and
![]() $p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
$p^r>3.436\times 10^{15}$
, then (1.1) has no solutions
![]() $(x,y,m,n)$
with (1.3). The proposition is proved.
$(x,y,m,n)$
with (1.3). The proposition is proved.
4 Proof of Theorem 1.1
We continue to assume that
![]() $r>s$
and that
$r>s$
and that
![]() $(x,y,m,n)$
is a solution of (1.1) with (1.3). Put
$(x,y,m,n)$
is a solution of (1.1) with (1.3). Put
![]() $m'=rm+s$
. By (3.25),
$m'=rm+s$
. By (3.25),
Since Proposition 3.3 implies that
![]() $p^s \le p^{r-1}<1.718\times 10^{15}$
, we see from (4.1) that
$p^s \le p^{r-1}<1.718\times 10^{15}$
, we see from (4.1) that
On the other hand, we deduce from Lemma 3.1 and (3.26) that
 $$ \begin{align} m'>\frac{n\log(p^s+1)}{\log p}>\frac{p^r \log(p^r+1)}{\log p}. \end{align} $$
$$ \begin{align} m'>\frac{n\log(p^s+1)}{\log p}>\frac{p^r \log(p^r+1)}{\log p}. \end{align} $$
Now, by (3.16),
where
 $$ \begin{align*} m'=rm+s,\quad \kappa=\frac{\log p}{\log(p^s+1)},\quad \mu=\frac{\log(p^r-1)}{\log(p^s+1)},\quad A=\frac{p^r-p^s-1}{\log(p^s+1)},\quad B=p. \end{align*} $$
$$ \begin{align*} m'=rm+s,\quad \kappa=\frac{\log p}{\log(p^s+1)},\quad \mu=\frac{\log(p^r-1)}{\log(p^s+1)},\quad A=\frac{p^r-p^s-1}{\log(p^s+1)},\quad B=p. \end{align*} $$
Lemma 4.1. Let
![]() $\kappa $
,
$\kappa $
,
![]() $\mu $
,
$\mu $
,
![]() $A>0$
and
$A>0$
and
![]() $B \ge 1$
be real numbers and let
$B \ge 1$
be real numbers and let
![]() $M'$
be a positive integer. Let
$M'$
be a positive integer. Let
![]() $p/q$
be a convergent of the continued fraction expansion of
$p/q$
be a convergent of the continued fraction expansion of
![]() $\kappa $
such that
$\kappa $
such that
![]() $q>6M'$
, and put
$q>6M'$
, and put
![]() $\varepsilon =\|\mu q\|-M'\| \kappa q\|$
, where
$\varepsilon =\|\mu q\|-M'\| \kappa q\|$
, where
![]() $\|\cdot \|$
denotes the distance from the nearest integer. If
$\|\cdot \|$
denotes the distance from the nearest integer. If
![]() $\varepsilon>0$
, then inequality (4.4) has no integer solution
$\varepsilon>0$
, then inequality (4.4) has no integer solution
![]() $(n,m')$
satisfying
$(n,m')$
satisfying
 $$ \begin{align*} \frac{\log(Aq/\varepsilon)}{\log B}\le m' \le M'. \end{align*} $$
$$ \begin{align*} \frac{\log(Aq/\varepsilon)}{\log B}\le m' \le M'. \end{align*} $$
Proof. Since the assertion is identical with that of [Reference Dujella and Pethő11, Lemma 5a] if the middle term of inequalities (4.4) is multiplied by
![]() $-1$
, the lemma is proved in the same way as [Reference Dujella and Pethő11, Lemma 5a].
$-1$
, the lemma is proved in the same way as [Reference Dujella and Pethő11, Lemma 5a].
By Proposition 3.3, (4.2) and (4.4), we may apply Lemma 4.1 with
![]() $M'=6.702\times 10^{15}$
in the ranges
$M'=6.702\times 10^{15}$
in the ranges
with
![]() $(p,s)\ne (2,1)$
, where
$(p,s)\ne (2,1)$
, where
![]() $R=3.436\times 10^{15}$
. For
$R=3.436\times 10^{15}$
. For
![]() $7 \le p <\sqrt {R}$
, the first step of reduction gives
$7 \le p <\sqrt {R}$
, the first step of reduction gives
![]() $m' \le 43$
, which contradicts (4.3) with
$m' \le 43$
, which contradicts (4.3) with
![]() $p \ge 7$
and
$p \ge 7$
and
![]() $r \ge 2$
. For
$r \ge 2$
. For
![]() $p=5$
, the first and second steps of reduction give
$p=5$
, the first and second steps of reduction give
![]() $m' \le 52$
and
$m' \le 52$
and
![]() $m' \le 30$
, respectively. The latter contradicts (4.3) with
$m' \le 30$
, respectively. The latter contradicts (4.3) with
![]() $p=5$
and
$p=5$
and
![]() $r \ge 2$
. For
$r \ge 2$
. For
![]() $p=3$
, the first and second steps of reduction give
$p=3$
, the first and second steps of reduction give
![]() $m' \le 75$
and
$m' \le 75$
and
![]() $m'\le 45$
, respectively, which, together with (4.3), yields
$m'\le 45$
, respectively, which, together with (4.3), yields
![]() $r=2$
. For
$r=2$
. For
![]() $p=2$
, the first and second steps of reduction give
$p=2$
, the first and second steps of reduction give
![]() $m' \le 126$
and
$m' \le 126$
and
![]() $m' \le 75$
, respectively, from which by (4.3) we obtain
$m' \le 75$
, respectively, from which by (4.3) we obtain
![]() $r \in \{3,4\}$
.
$r \in \{3,4\}$
.
Thus, it remains to consider the cases where
In view of the bounds for
![]() $m'=rm+s$
obtained above, it suffices to check that (3.14) with (4.5) has no solution
$m'=rm+s$
obtained above, it suffices to check that (3.14) with (4.5) has no solution
![]() $(m,n)$
in the ranges
$(m,n)$
in the ranges
![]() $m \le 24$
and
$m \le 24$
and
![]() $n \le 34$
, which can be easily done. Therefore, the theorem is proved.
$n \le 34$
, which can be easily done. Therefore, the theorem is proved.
Acknowledgement
The authors thank the anonymous referee for suggesting the addition of a connection between Theorem 1.1 and the results in [Reference Leung, Ma and Schmidt19], which led to Corollary 1.2.