No CrossRef data available.
Article contents
ON MONOTONE INCREASING REPRESENTATION FUNCTIONS
Published online by Cambridge University Press: 17 July 2023
Abstract
Let 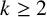 $k\ge 2$ be an integer and let A be a set of nonnegative integers. The representation function
$k\ge 2$ be an integer and let A be a set of nonnegative integers. The representation function 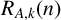 $R_{A,k}(n)$ for the set A is the number of representations of a nonnegative integer n as the sum of k terms from A. Let
$R_{A,k}(n)$ for the set A is the number of representations of a nonnegative integer n as the sum of k terms from A. Let 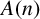 $A(n)$ denote the counting function of A. Bell and Shallit [‘Counterexamples to a conjecture of Dombi in additive number theory’, Acta Math. Hung., to appear] recently gave a counterexample for a conjecture of Dombi and proved that if
$A(n)$ denote the counting function of A. Bell and Shallit [‘Counterexamples to a conjecture of Dombi in additive number theory’, Acta Math. Hung., to appear] recently gave a counterexample for a conjecture of Dombi and proved that if 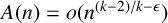 $A(n)=o(n^{{(k-2)}/{k}-\epsilon })$ for some
$A(n)=o(n^{{(k-2)}/{k}-\epsilon })$ for some 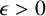 $\epsilon>0$, then
$\epsilon>0$, then 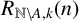 $R_{\mathbb {N}\setminus A,k}(n)$ is eventually strictly increasing. We improve this result to
$R_{\mathbb {N}\setminus A,k}(n)$ is eventually strictly increasing. We improve this result to 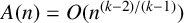 $A(n)=O(n^{{(k-2)}/{(k-1)}})$. We also give an example to show that this bound is best possible.
$A(n)=O(n^{{(k-2)}/{(k-1)}})$. We also give an example to show that this bound is best possible.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the NKFIH Grant No. K129335; the second author was supported by the NKFIH Grant No. K129335.


