No CrossRef data available.
Article contents
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
Part of:
Multiplicative number theory
Exponential sums and character sums
Algebraic number theory: global fields
Published online by Cambridge University Press: 29 June 2023
Abstract
Let 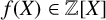 $f(X) \in {\mathbb Z}[X]$ be a polynomial of degree
$f(X) \in {\mathbb Z}[X]$ be a polynomial of degree 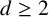 $d \ge 2$ without multiple roots and let
$d \ge 2$ without multiple roots and let 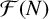 ${\mathcal F}(N)$ be the set of Farey fractions of order N. We use bounds for some new character sums and the square-sieve to obtain upper bounds, pointwise and on average, on the number of fields
${\mathcal F}(N)$ be the set of Farey fractions of order N. We use bounds for some new character sums and the square-sieve to obtain upper bounds, pointwise and on average, on the number of fields 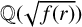 ${\mathbb Q}(\sqrt {f(r)})$ for
${\mathbb Q}(\sqrt {f(r)})$ for 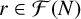 $r\in {\mathcal F}(N)$, with a given discriminant.
$r\in {\mathcal F}(N)$, with a given discriminant.
MSC classification
Primary:
11L40: Estimates on character sums
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
During the preparation of this work, the author was supported by the Australian Research Council Grant DP200100355.
References
Banks, W. D. and Shparlinski, I. E., ‘On coincidences among quadratic fields generated by the Shanks sequence’, Q. J. Math. 68 (2017), 465–484.Google Scholar
Bilu, Y., ‘Counting number fields in fibers (with an Appendix by Jean Gillibert)’, Math. Z. 288 (2018), 541–563.CrossRefGoogle Scholar
Bilu, Y. and Gillibert, J., ‘Chevalley–Weil theorem and subgroups of class groups’, Israel J. Math. 226 (2018), 927–956.CrossRefGoogle Scholar
Bilu, Y. and Luca, F., ‘Diversity in parametric families of number fields’, in: Number Theory—Diophantine Problems, Uniform Distribution and Applications (eds. Elsholtz, C. and Grabner, P.) (Springer, Cham, 2017), 169–191.CrossRefGoogle Scholar
Cutter, P., Granville, A. and Tucker, T. J., ‘The number of fields generated by the square root of values of a given polynomial’, Canad. Math. Bull. 46 (2003), 71–79.CrossRefGoogle Scholar
Dvornicich, R. and Zannier, U., ‘Fields containing values of algebraic functions’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 21 (1994), 421–443.Google Scholar
Heath-Brown, D. R., ‘The square sieve and consecutive square-free numbers’, Math. Ann. 266 (1984), 251–259.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘A mean value estimate for real character sums’, Acta Arith. 72 (1995), 235–275.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Kulkarni, K. and Levin, A., ‘Hilbert’s irreducibility theorem and ideal class groups of quadratic fields’, Acta Arith., to appear.Google Scholar
Luca, F. and Shparlinski, I. E., ‘Discriminants of complex multiplication fields of elliptic curves over finite fields’, Canad. Math. Bull. 50 (2007), 409–417.CrossRefGoogle Scholar
Luca, F. and Shparlinski, I. E., ‘Quadratic fields generated by polynomials’, Archiv Math. 91 (2008), 399–408.CrossRefGoogle Scholar
Patterson, R. D., van der Poorten, A. J. and Williams, H. C., ‘Characterization of a generalized Shanks sequence’, Pacific J. Math. 230 (2007), 185–215.CrossRefGoogle Scholar
Stewart, C. L. and Top, J., ‘On ranks of twists of elliptic curves and power-free values of binary forms’, J. Amer. Math. Soc. 8 (1995), 943–973.CrossRefGoogle Scholar
van der Poorten, A. J. and Williams, H. C., ‘On certain continued fraction expansions of fixed period length’, Acta Arith. 89 (1999), 23–35.CrossRefGoogle Scholar
Williams, H. C., ‘Some generalizations of the
 ${S}_n$
sequence of Shanks’, Acta Arith.
69 (1995), 199–215.CrossRefGoogle Scholar
${S}_n$
sequence of Shanks’, Acta Arith.
69 (1995), 199–215.CrossRefGoogle Scholar


