Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T15:51:40.248Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOME SUBCLASSES OF HARMONIC MAPPINGS

Part of: Geometric function theory

Published online by Cambridge University Press:  10 July 2019

NIRUPAM GHOSH Open the ORCID record for NIRUPAM GHOSH [Opens in a new window]  and
VASUDEVARAO ALLU Open the ORCID record for VASUDEVARAO ALLU [Opens in a new window]
NIRUPAM GHOSH
Affiliation:
Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721 302, West Bengal, India email nirupamghoshmath@gmail.com
VASUDEVARAO ALLU*
Affiliation:
School of Basic Science, Indian Institute of Technology Bhubaneswar, Bhubaneswar 752 050, Odisha, India email avrao@iitbbs.ac.in
*
✉avrao@iitbbs.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 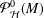${\mathcal{P}}_{{\mathcal{H}}}^{0}(M)$ denote the class of normalised harmonic mappings 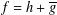$f=h+\overline{g}$ in the unit disk 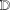$\mathbb{D}$ satisfying 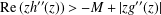$\text{Re}\,(zh^{\prime \prime }(z))>-M+|zg^{\prime \prime }(z)|$, where 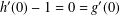$h^{\prime }(0)-1=0=g^{\prime }(0)$ and 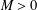$M>0$. Let 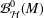${\mathcal{B}}_{{\mathcal{H}}}^{0}(M)$ denote the class of sense-preserving harmonic mappings 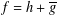$f=h+\overline{g}$ in the unit disk 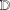$\mathbb{D}$ satisfying 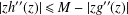$|zh^{\prime \prime }(z)|\leq M-|zg^{\prime \prime }(z)|$, where 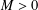$M>0$. We discuss the coefficient bound problem, the growth theorem for functions in the class 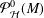${\mathcal{P}}_{{\mathcal{H}}}^{0}(M)$ and a two-point distortion property for functions in the class 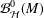${\mathcal{B}}_{{\mathcal{H}}}^{0}(M)$.

Keywords

analyticunivalentstarlikeconvexclose-to-convexharmonic mappingconvolutionright half-plane mapping

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30C50: Coefficient problems for univalent and multivalent functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 130 - 140
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleman, A. and Constantin, A., ‘Harmonic maps and ideal fluid flows’, Arch. Ration. Mech. Anal. 204 (2012), 479–513.10.1007/s00205-011-0483-2Google Scholar
Bazilevich, I. E., ‘The problem of coefficients of univalent functions’, Math. J. Aviat. Inst. (Moscow) (1945), 29–47.Google Scholar
Bshouty, D., Joshi, S. S. and Joshi, S. B., ‘On close-to-convex harmonic mappings’, Complex Var. Elliptic Equ. 58 (2013), 1195–1199.10.1080/17476933.2011.647002Google Scholar
Clunie, J. and Sheil-Small, T., ‘Harmonic univalent functions’, Ann. Acad. Sci. Fenn. Ser. A I 9 (1984), 3–25.Google Scholar
Constantin, O. and Martin, M. J., ‘A harmonic maps approach to fluid flows’, Math. Ann. 369 (2017), 1–16.10.1007/s00208-016-1435-9Google Scholar
Ghosh, N. and Vasudevarao, A., ‘Some basic properties of certain subclass of harmonic univalent functions’, Complex Var. Elliptic Equ. 63(12) (2018), 1687–1703.10.1080/17476933.2017.1403426Google Scholar
Kalaj, D., Ponnusamy, S. and Vuorinen, M., ‘Radius of close-to-convexity and full starlikeness of harmonic mappings’, Complex Var. Elliptic Equ. 59 (2014), 539–552.10.1080/17476933.2012.759565Google Scholar
Kim, S. A. and Minda, D., ‘Two-point distortion theorems for univalent functions’, Pacific J. Math. 163 (1994), 137–157.10.2140/pjm.1994.163.137Google Scholar
Nagpal, S. and Ravichandran, V., ‘Fully starlike and fully convex harmonic mappings of order 𝛼’, Ann. Polon. Math. 108 (2013), 85–107.10.4064/ap108-1-7Google Scholar
Ponnusamy, S., Sairam Kaliraj, A. and Starkov, V. V., ‘Sections of univalent harmonic mappings’, Indag. Math. 28 (2017), 527–540.10.1016/j.indag.2017.01.001Google Scholar
Ponnusamy, S., Sairam Kaliraj, A. and Starkov, V. V., ‘Coefficients of univalent harmonic mappings’, Monatsh. Math. 186(3) (2018), 453–470.10.1007/s00605-017-1038-xGoogle Scholar
Ponnusamy, S., Vasudevarao, A. and Vuorinen, M., ‘Region of variability for certain classes of univalent functions satisfying differential inequalities’, Complex Var. Elliptic Equ. 54 (2009), 899–922.10.1080/17476930802657616Google Scholar
Sairam Kaliraj, A., ‘Injectivity of sections of close-to-convex harmonic mappings with convex analytic part’, Probl. Anal. Issues Anal. 7(25, No. 2) (2018), 131–143.10.15393/j3.art.2018.5830Google Scholar
Starkov, V. V., ‘Univalence of harmonic functions, problem of Ponnusamy and Sairam, and constructions of univalent polynomials’, Probl. Anal. Issues Anal. 3(21, No. 2) (2014), 59–73.10.15393/j3.art.2014.2729Google Scholar
Wang, X.-T. and Liang, X.-Q., ‘Precise coefficient estimates for close-to-convex harmonic univalent mappings’, J. Math. Anal. Appl. 263 (2001), 501–509.Google Scholar