Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T14:10:20.825Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE FACTORISATION OF 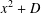$x^{2}+D$

Part of: Diophantine equations

Published online by Cambridge University Press:  27 May 2019

AMIR GHADERMARZI Open the ORCID record for AMIR GHADERMARZI [Opens in a new window]
AMIR GHADERMARZI*
Affiliation:
School of Mathematics, Statistics and Computer Science, College of Science, University of Tehran, Tehran, Iran School of Mathematics, Institute for Research in Fundamental Science (IPM), P.O. Box 19395-5746, Tehran, Iran email a.ghadermarzi@ut.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 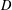$D$ be a positive nonsquare integer, 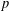$p$ a prime number with 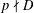$p\nmid D$ and 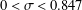$0<\unicode[STIX]{x1D70E}<0.847$. We show that there exist effectively computable constants 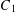$C_{1}$ and 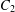$C_{2}$ such that if there is a solution to 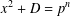$x^{2}+D=p^{n}$ with 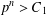$p^{n}>C_{1}$, then for every 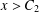$x>C_{2}$ with 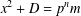$x^{2}+D=p^{n}m$ we have 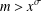$m>x^{\unicode[STIX]{x1D70E}}$. As an application, we show that for 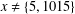$x\neq \{5,1015\}$, if the equation 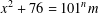$x^{2}+76=101^{n}m$ holds, then 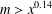$m>x^{0.14}$.

Keywords

hypergeometric methodPadé approximantRamanujan–Nagell equation

MSC classification

Primary: 11D61: Exponential equations
Secondary: 11D75: Diophantine inequalities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 206 - 215
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was in part supported by a grant from IPM (No. 95110044).

References

Bauer, M. and Bennett, M., ‘Applications of the hypergeometric method to the generalized Ramanujan–Nagell equation’, Ramanujan J. 6(2) (2002), 209–270.Google Scholar
Bennett, M., ‘Fractional parts of powers of rational numbers’, Math. Proc. Cambridge Philos. Soc. 114(2) (1993), 191–201.10.1017/S0305004100071528Google Scholar
Bennett, M. A., Filaseta, M. and Trifonov, O., ‘Yet another generalization of the Ramanujan–Nagell equation’, Acta Arith. 134(3) (2008), 211–217.Google Scholar
Bennett, M. A., Filaseta, M. and Trifonov, O., ‘On the factorization of consecutive integers’, J. reine angew. Math. 629 (2009), 171–200.Google Scholar
Beukers, F., ‘On the generalized Ramanujan–Nagell equation. I’, Acta Arith. 38(4) (1980–1981), 389–410.Google Scholar
Beukers, F., ‘On the generalized Ramanujan–Nagell equation. II’, Acta Arith. 39(2) (1981), 113–123.Google Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Classical and modular approaches to exponential Diophantine equations. II. The Lebesgue–Nagell equation’, Compos. Math. 142(1) (2006), 31–62.10.1112/S0010437X05001739Google Scholar
Gross, S. S. and Vincent, A. F., ‘On the factorization of f (n) for f (x) in ℤ[x]’, Int. J. Number Theory 9(5) (2013), 1225–1236.Google Scholar
Mahler, K., Lectures on Diophantine Approximations. Part I: G-adic Numbers and Roth’s Theorem (University of Notre Dame Press, Notre Dame, IN, 1961), prepared from the notes by R. P. Bambah of lectures given at the University of Notre Dame in the fall of 1957.Google Scholar
Stewart, C. L., ‘A note on the product of consecutive integers’, in: Topics in Classical Number Theory, Vols. I, II (Budapest, 1981), Colloquium Mathematicum Societatis János Bolyai, 34 (North-Holland, Amsterdam, 1984), 1523–1537.Google Scholar