Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T05:12:39.806Z Has data issue: false hasContentIssue false
  • English
  • Français

(ANTI)COMMUTATIVE ALGEBRAS WITH A MULTIPLICATIVE BASIS

Part of: General nonassociative rings Lie algebras and Lie superalgebras Basic linear algebra

Published online by Cambridge University Press:  15 December 2014

ANTONIO J. CALDERÓN MARTÍN
ANTONIO J. CALDERÓN MARTÍN*
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Cádiz, Campus de Puerto Real, 11510 Puerto Real, Cádiz, Spain email ajesus.calderon@uca.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A basis 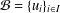${\mathcal{B}}=\{u_{i}\}_{i\in I}$ of a commutative or anticommutative algebra 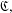$\mathfrak{C},$ over an arbitrary base field 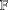$\mathbb{F}$, is called multiplicative if for any 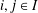$i,j\in I$ we have that 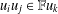$u_{i}u_{j}\in \mathbb{F}u_{k}$ for some 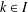$k\in I$. We show that if a commutative or anticommutative algebra 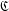$\mathfrak{C}$ admits a multiplicative basis then it decomposes as the direct sum 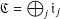$\mathfrak{C}=\bigoplus _{j}\mathfrak{i}_{j}$ of well-described ideals each one of which admits a multiplicative basis. Also the minimality of 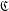$\mathfrak{C}$ is characterised in terms of the multiplicative basis and it is shown that, under a mild condition, the above direct sum is indexed by the family of its minimal ideals admitting a multiplicative basis.

Keywords

commutative algebraanticommutative algebramultiplicative basisinfinite-dimensional algebrastructure theory

MSC classification

Primary: 17A60: Structure theory
Secondary: 15A03: Vector spaces, linear dependence, rank 17B05: Structure theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 211 - 218
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abdesselam, B., ‘The twisted Heisenberg algebra U h, w(H (4))’, J. Math. Phys. 38(12) (1997), 6045–6060.CrossRefGoogle Scholar
Bautista, R., Gabriel, P., Roiter, A. V. and Salmeron, L., ‘Representation-finite algebras and multiplicative basis’, Invent. Math. 81 (1985), 217–285.Google Scholar
Bovdi, A. A., ‘Cross products of semigroups and rings’, Sibirsk. Mat. Zh. 4 (1963), 481–499 (in Russian).Google Scholar
Bovdi, V., ‘On filtered multiplicative bases of group algebras. II’, Algebr. Represent. Theory 6(3) (2003), 353–368.Google Scholar
Bovdi, V., Grishkov, A. and Siciliano, S., ‘Filtered multiplicative bases of restricted enveloping algebras’, Algebr. Represent. Theory 14(4) (2011), 601–608.Google Scholar
Calderón, A. J., ‘On split Lie algebras with a symmetric root system’, Proc. Indian Acad. Sci. Math. Sci. 118(3) (2008), 351–356.Google Scholar
Calderón, A. J., ‘On the structure of split non-commutative Poisson algebras’, Linear Multilinear Algebra 60(7) (2012), 775–785.Google Scholar
Calderón, A. J. and Sánchez, J. M., ‘On the structure of split Lie color algebras’, Linear Algebra Appl. 436(2) (2012), 307–315.CrossRefGoogle Scholar
Calderón, A. J. and Sánchez, J. M., ‘Split Leibniz algebras’, Linear Algebra Appl. 436(6) (2012), 1648–1660.Google Scholar
Elduque, A., ‘A Lie grading which is not a semigroup grading’, Linear Algebra Appl. 418 (2006), 312–314.Google Scholar
Elduque, A., ‘More non semigroup Lie gradings’, Linear Algebra Appl. 431(9) (2009), 1603–1606.Google Scholar
Kupisch, H. and Waschbusch, J., ‘On multiplicative basis in quasi-Frobenius algebras’, Math. Z. 186 (1984), 401–405.Google Scholar
Makhlouf, A., ‘Hom-alternative algebras and Hom-Jordan algebras’, Int. Electron. J. Algebra 8 (2010), 177–190.Google Scholar
Mollov, T. Z. and Nachev, N. A., ‘On the commutative twisted group algebras’, Comm. Algebra 35(10) (2007), 3064–3070.Google Scholar
Ren, B. and Ji Meng, D., ‘Some 2-step nilpotent Lie algebras I’, Linear Algebra Appl. 338 (2001), 77–98.Google Scholar
Sagle, A. A., ‘On simple extended Lie algebras over fields of characteristic zero’, Pacific J. Math. 15(2) (1965), 621–648.CrossRefGoogle Scholar
Schue, J. R., ‘Hilbert space methods in the theory of Lie algebras’, Trans. Amer. Math. Soc. 95 (1960), 69–80.Google Scholar
Smith, H. A., ‘Commutative twisted group algebras’, Trans. Amer. Math. Soc. 197 (1974), 315–326.Google Scholar
Stumme, N., ‘The structure of locally finite split Lie algebras’, J. Algebra 220 (1999), 664–693.CrossRefGoogle Scholar