Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:03:09.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcating attractors and Galerkin approximates

Published online by Cambridge University Press:  17 April 2009

R. Wells  and
J. A. Dutton
R. Wells
Affiliation:
Department of Mathematics, College of Science, The Pennsylvania State University, 215 McAllister Building, University Park, Pennsylvania, 16802, United States of America.
J. A. Dutton
Affiliation:
Department of Mathematics, College of Science, The Pennsylvania State University, 215 McAllister Building, University Park, Pennsylvania, 16802, United States of America.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let = A0u + μA1u + J (u) be a Navier-Stokes parameterized evolution equation in a Hilbert space H and let F1 ⊂ F2 ⊂ F3 ⊂ … be an increasing sequence of finite dimensional spaces such that every Fn ⊕ ℝ contains the center-unstable linear subspace Hu ⊕ ℝ ⊂ H ⊕ ℝ of the system = A0u + μA1u + J (u), = 0. Then each Fn ⊕ ℝ determines a Galerkin approximant of the original system, with the same center-unstable linear subspace Hu ⊕ ℝ The flow on the center-unstable manifold of the original system may be identified with a parameterized flow on Hu given by x = f∞ (x,μ). The flow on the center-unstable manifold of the Galerkin approximant determined by Fn ⊕ ℝ may be identified with a parameterized flow on Hu given by ẋ = fn (x,μ). It is proved that Theorem I holds: 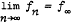in the Cktopology on a compact neighborhood of the origin in Hu ⊕ ℝ From this theorem it is concluded that Theorem 2 holds: If a certain priori bound holds relating f∞ and fn and an asymptotically stable set A of ẋ = fn (x,μ) near the origin, then ẋ = f∞ (x,μ) has an asymptotically stable set near the origin with the same Borsuk shape as A. Conversely, for each asymptotically stable set near the origin of ẋ = f∞(x,μ), there is one of the same Borsuk shape for ẋ = fn (x,μ) provided n is large enough. Informally, these results amount to the statement that asymptotically stable sets of the Navier-stokes equation, bifurcating from a steady solution, are recovered up to Borsuk shape by those of large enough Galerkin approximants.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 35 , Issue 3 , June 1987 , pp. 321 - 347
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Birkhoff, G.D., “Sur quelques courbes fermees remarquables”, Bull. Soc. Math. France 60 (1932), 1–26.Google Scholar
[2]Borsuk, K., The Theory of Shape, (Polish Scientific Publishers, Warsaw, 1975).Google Scholar
[3]Constantin, P., Foias, C., and Temam, R., “On the large time Galerkin approximation of the Navier-Stokes equations”, SIAM J. Numer. Anal. 21 (1984), 615–634.CrossRefGoogle Scholar
[4]Dutton, J.A., “Fundamental theorems of climate theory – some proved, some conjectured”, SIAM Rev. 24 (1982), 1–33.Google Scholar
[5]Dutton, J.A. and Wells, R., “Topological issues in hydrodynamic predictability”, Predictability of Fluid Motions, (AIP Proceedings No. 106, Holloway, G. and West, B.J. Eds. 1984), 11–43.Google Scholar
[6]Guckenheimer, J., and Holmes, P., Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields, (Springer Verlag, New York, 1983).Google Scholar
[7]Hirsch, M.W., and Mazur, B.C., Smoothings of Piecewiselinear Manifolds, (Annals of Mathematics Studies 80 Princeton, 1984).Google Scholar
[8]Kloeden, P.E., “Asymptotically stable attracting sets in the Navier-Stokes equations”, Bull. Austral. Math. Soc. 34 (1986), 37–52.Google Scholar
[9]Ladyshenskaya, O., The Mathematical Theory of Viscous Incompressible Flow, (Gordon and Breach, New York, 1969).Google Scholar
[10]Lorenz, E.N., “Deterministic non-periodic flow”, J. Atmospheric Sci. 20 (1963), 130–141.2.0.CO;2>CrossRefGoogle Scholar
[11]Marsden, J.E. and McCracken, M., The Hopf Bifurcation and Its Applications, (Springer Verlag, New York, 1976).CrossRefGoogle Scholar
[12]Nese, J., Lyapunov dimension in meteorological finite truncated models, (Masters Thesis, The Pennsylvania State University, 1985).Google Scholar
[13]Ostlund, S., Rand, D., Sethna, J. and Siggia, E., “Universal properties of the transition from quasi-periodicity to chaos in dissipative systems”, Physica 8D (1983), 303–342.Google Scholar
[14]Poston, T., and Stewart, I., Catastrophe Theory and Its Applications, (Pitman, London 1978).Google Scholar
[15]Pugh, C.C., and Shub, M., “Suspending subshifts”, Contributions to Analysis and Geometry, (Johns Hopkins Univ. Press, Baltimore, 1981), 265–275.Google Scholar
[16]Temam, R., Navier-Stokes Equations and Nonlinear Functional Analysis,(CBMS-NSF Regional Conference Series in Applied Mathematics 41SIAM,1983).Google Scholar
[17]Weissler, F., “Semilinear evolution equations in Banach spaces”, J. Funct. Anal. 32 (1979), 277–296.Google Scholar
[18]Williams, R., “The structure of Lorenz attractors”, Publ. Math. Inst. Hantes Etud. Sci. 50 (1979), 73–99.Google Scholar
[19]Wilson, F.W., “Smoothing derivatives of functions and applications”, Trans. Amer. Math. Soc. 139 (1969), 413–428.Google Scholar