Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T19:42:46.179Z Has data issue: false hasContentIssue false
  • English
  • Français

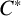$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS

Part of: Topological and differentiable algebraic systems Linear spaces and algebras of operators Selfadjoint operator algebras

Published online by Cambridge University Press:  13 January 2025

ROHIT DILIP HOLKAR Open the ORCID record for ROHIT DILIP HOLKAR [Opens in a new window]  and
MD AMIR HOSSAIN Open the ORCID record for MD AMIR HOSSAIN [Opens in a new window]
ROHIT DILIP HOLKAR
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India e-mail: rohit.d.holkar@gmail.com
MD AMIR HOSSAIN*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India Current affiliation: The Institute of Mathematical Sciences, A CI of Homi Bhabha National Institute, 4th cross street, CIT Campus, Taramani, Chennai, 600113, India
*
e-mail: mdamirhossain18@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a possibly unsaturated Fell bundle $\mathcal {A}\to G$ over a locally compact, possibly non-Hausdorff, groupoid G. We list four notions of continuity of representations of 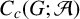$\mathit {C_c}(G;\mathcal {A})$ on a Hilbert space and prove their equivalence. This allows us to define the full $\mathit {C}^*$-algebra of the Fell bundle in different ways.

Keywords

representationsétale groupoidsFell bundlesC*-algebras

MSC classification

Primary: 47L55: Representations of (nonselfadjoint) operator algebras
Secondary: 22A22: Topological groupoids (including differentiable and Lie groupoids) 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the SERB grant MTR/2020/000198 of the first author and the CSIR grant 09/1020(0159)/2019-EMR-I of the second author.

References

Anantharaman-Delaroche, C., ‘Partial actions of groupoids’, Preprint, 2020, hal-02429386.Google Scholar
Brown, L. G., Mingo, J. A. and Shen, N.-T., ‘Quasi-multipliers and embeddings of Hilbert ${C}^{\ast }$ -bimodules’, Canad. J. Math. 46 (1994), 1150–1174.CrossRefGoogle Scholar
Clark, L. O. and Zimmerman, J., ‘A Steinberg algebra approach to étale groupoid ${C}^{\ast }$ -algebras’, J. Operator Theory 91 (2024), 349–371.Google Scholar
Connes, A., ‘A survey of foliations and operator algebras’, in: Operator Algebras and Applications, Part 1 (Kingston, ON, 1980), Proceedings of Symposia in Pure Mathematics, 38 (ed. Kadison, R. V.) (American Mathematical Society, Providence, RI, 1982), 521–628.CrossRefGoogle Scholar
Dixmier, J., ${C}^{\ast }$ -Algebras, North-Holland Mathematical Library, 15 (North-Holland Publishing Co., Amsterdam–New York–Oxford, 1977), translated from the French by F. Jellett.Google Scholar
Exel, R., ‘Twisted partial actions: a classification of regular ${C}^{\ast }$ -algebraic bundles’, Proc. Lond. Math. Soc. (3) 74 (1997), 417–443.CrossRefGoogle Scholar
Exel, R., ‘Inverse semigroups and combinatorial ${C}^{\ast }$ -algebras’, Bull. Braz. Math. Soc. (N.S.) 39 (2008), 191–313.CrossRefGoogle Scholar
Exel, R., Partial Dynamical Systems, Fell Bundles and Applications, Mathematical Surveys and Monographs, 224 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Fell, J. M. G. and Doran, R. S., Representations of ${}^{\ast }$ -Algebras, Locally Compact Groups, and Banach ${}^{\ast }$ -Algebraic Bundles, Vols. 1 and 2, Pure and Applied Mathematics (Academic Press, New York, 1988).Google Scholar
Hofmann, K. H., ‘Bundles and sheaves are equivalent in the category of Banach spaces’, in: $K$ -theory and Operator Algebras (Proc. Conf., Univ. Georgia, Athens, GA, 1975), Lecture Notes in Mathematics, 575 (eds. Morel, B. B. and Singer, I. M.) (Springer, Berlin, 1977), 53–69.Google Scholar
Kumjian, A., ‘Fell bundles over groupoids’, Proc. Amer. Math. Soc. 126 (1998), 1115–1125.CrossRefGoogle Scholar
Muhly, P. S. and Williams, D. P., ‘Equivalence and disintegration theorems for Fell bundles and their ${C}^{\ast }$ -algebras’, Dissertationes Math. (Rozprawy Mat.) 456 (2008), 1–57.CrossRefGoogle Scholar
Paterson, A. L. T., Groupoids, Inverse Semigroups, and their Operator Algebras, Progress in Mathematics, 170 (Birkhäuser Boston, Inc., Boston, MA, 1999).CrossRefGoogle Scholar
Renault, J., A Groupoid Approach to ${C}^{\ast }$ -algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin, 1980).Google Scholar
Renault, J., ‘Représentation des produits croisés d’algèbres de groupoïdes’, J. Operator Theory 18 (1987), 67–97.Google Scholar
Sims, A., Szabó, G. and Williams, D., Operator Algebras and Dynamics: Groupoids, Crossed Products and Rokhlin Dimension, Advanced Courses in Mathematics, CRM Barcelona (ed. Perera, F.) (Birkhäuser/Springer, Cham, 2020).CrossRefGoogle Scholar