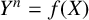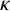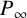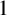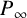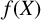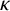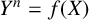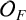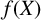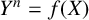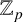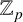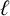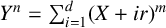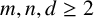DIOPHANTINE EQUATIONS OF THE FORM $Y^n=f(X)$ OVER FUNCTION FIELDS

Abstract

Let $\ell $ and p be (not necessarily distinct) prime numbers and F be a global function field of characteristic $\ell $ with field of constants $\kappa $. Assume that there exists a prime $P_\infty $ of F which has degree $1$ and let $\mathcal {O}_F$ be the subring of F consisting of functions with no poles away from $P_\infty $. Let $f(X)$ be a polynomial in X with coefficients in $\kappa $. We study solutions to Diophantine equations of the form $Y^{n}=f(X)$ which lie in $\mathcal {O}_F$ and, in particular, show that if m and $f(X)$ satisfy additional conditions, then there are no nonconstant solutions. The results apply to the study of solutions to $Y^{n}=f(X)$ in certain rings of integers in $\mathbb {Z}_{p}$-extensions of F known as constant $\mathbb {Z}_p$-extensions. We prove similar results for solutions in the polynomial ring $K[T_1, \ldots , T_r]$, where K is any field of characteristic $\ell $, showing that the only solutions must lie in K. We apply our methods to study solutions of Diophantine equations of the form $Y^n=\sum _{i=1}^d (X+ir)^m$, where $m,n, d\geq 2$ are integers.

1 Introduction

Let $n\geq 2$ be an integer and $\kappa $ be a finite field of characteristic $\ell>0$ . Let F be a global function field with field of constants $\kappa $ and assume that there exists a prime $P_\infty $ of F of degree $1$ . In other words, we assume that there is a prime $P_\infty $ which is totally inert in the composite $\bar {\kappa }\cdot F$ . The ring of integers $\mathcal {O}_F$ consists of all functions $f\in F$ with no poles away from $P_\infty $ . Given a polynomial $f(X)$ with coefficients in $\kappa $ , we study solutions to the superelliptic Diophantine equation $Y^n=f(X)$ for which both X and Y lie in $\mathcal {O}_F$ . Superelliptic equations over function fields form an important part of the modern theory of Diophantine equations. There has been significant interest in proving finiteness results, as well as in obtaining effective bounds for the number of solutions. Over algebraic number fields, the equation $Y^n=f(X)$ was shown by LeVeque in 1964 to have finitely many solutions, provided certain additional conditions are met (see [10, Theorem 1]). Brindza [6] later obtained an effective bound on the number of solutions to such superelliptic equations. For further details, we refer the reader to [16, Ch. 8]. In the function field case, effective bounds on the number of solutions were obtained by Mason and Brindza [11, page 168]. In greater detail, given a solution $(X,Y)$ to $Y^n=f(X)$ , this result provides an effective upper bound on the height of X in terms of the genus of the function field F [11, page 166, l.21].

We consider the class of superelliptic Diophantine equations $Y^n=f(X)$ , for which the coefficients of $f(X)$ lie in the field of constants. We derive conditions for there to be no nonconstant solutions. Given a natural number N, denote by $h_F[N]$ the cardinality of the N-torsion in the class group of F. The understanding here is that $h_F[1]=1$ .

Theorem 1.1 (Theorem 2.4).

Let $\ell $ be a prime number and F be a global function field of characteristic $\ell $ . Let $\mathcal {O}_F$ be the ring of integers of F. Denote by $\kappa $ the field of constants of F. Let $f(X)$ be a polynomial with coefficients in $\kappa $ . Let $q\neq \ell $ be a prime number and let $k>0$ be the least integer such that $h_F[q^k]=h_F[q^{k-1}]$ . Assume that the following conditions are satisfied:

1. (1) $f(X)$ factorises into $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$ , where $a_0\in \kappa $ , $a_1,\ldots , a_t$ are distinct elements in $\kappa $ , $n_1,\ldots , n_t$ are positive integers and $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Then any solution $(X,Y)$ to

$$ \begin{align*} Y^{q^k}=f(X) \end{align*} $$

for which $X,Y\in \mathcal {O}_F$ is constant, that is, X and Y are both in $\kappa $ .

We shall apply our analysis to study a class of Diophantine equations which involve perfect powers in arithmetic progressions. Let $m, n, d\geq 2$ be integers and let $r\geq 1$ . There has been significant interest in the classification of integral solutions to the Diophantine equation

$$ \begin{align*}Y^n=(X+r)^m+(X+2r)^m+\cdots+(X+dr)^m\end{align*} $$

(see [1–5, 7, 8, 13]).

We also explore themes motivated by the Iwasawa theory of function fields. Mazur [12] initiated the Iwasawa theory of elliptic curves over number fields, which had applications to the growth of Mordell–Weil ranks of elliptic curves in certain infinite towers of number fields. One hopes to extend such lines of investigation to curves of higher genus (see [14]) and, more generally, to study the stability and growth of solutions to any Diophantine equation in an infinite tower of global fields. We study certain function field analogues of such questions. However, instead of elliptic curves, we consider the class of superelliptic equations of the form $Y^n=f(X)$ , where $f(X)$ has constant coefficients. Let us explain our results in greater detail. Given any integer n, there is a unique extension $\kappa _n/\kappa $ such that $\operatorname {Gal}(\kappa _n/\kappa )$ is isomorphic to $\mathbb {Z}/n\mathbb {Z}$ . Given a prime p, set $\kappa _n^{(p)}$ to denote $\kappa _{p^n}$ and set $F_n^{(p)}$ to denote the composite $F\cdot \kappa _n^{(p)}$ . This gives rise to a tower of function field extensions

$$ \begin{align*}F=F_0^{(p)}\subset F_1^{(p)}\subset \cdots \subset F_n^{(p)}\subset F_{n+1}^{(p)}\subset \cdots. \end{align*} $$

Let $\mathbb {Z}_p$ denote the ring of p-adic integers, that is, the valuation ring of $\mathbb {Q}_p$ . The constant $\mathbb {Z}_p$ -extension of F is the infinite union

$$ \begin{align*}F_\infty^{(p)}:=\bigcup_{n} F_n^{(p)}.\end{align*} $$

It is easy to see that the Galois group $\operatorname {Gal}(F_\infty ^{(p)}/F)$ is isomorphic to $\mathbb {Z}_{p}$ . Let $h_F$ denote the class number of F (see [15, Ch. 5]). Note that since $P_\infty $ is assumed to have degree $1$ , it remains inert in $F_n^{(p)}$ for all p. Let $\mathcal {O}_{\infty }^{(p)}$ and $\mathcal {O}_{n}^{(p)}$ respectively be the rings of integers of $F_\infty ^{(p)}$ and $F_n^{(p)}$ , that is, the functions $f\in F_\infty $ with no poles away from $P_\infty $ . We now state our main result.

Theorem 1.2 (Theorem 3.2).

Let $\ell $ be a prime number and F be a global function field of characteristic $\ell $ . Let $\kappa $ be the field of constants of F and let p and q be prime numbers that are not necessarily distinct. Assume that $q\neq \ell $ . Let $f(X)$ be a polynomial with coefficients in $\kappa $ satisfying the following conditions:

1. (1) the polynomial $f(X)$ factorises into $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$ , where $a_0\in \kappa $ , $a_1,\ldots , a_t$ are distinct elements in $\kappa $ , $n_1,\ldots , n_t$ are positive integers and $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Then the following assertions hold.

1. (i) Suppose that p and q are distinct. Then, for all sufficiently large numbers $k>0$ , the only solutions $(X,Y)$ to $Y^{q^k}=f(X)$ that are contained in $\mathcal {O}_\infty ^{(p)}$ are constant.

2. (ii) Suppose that $p\nmid h_F$ . Then the only solutions $(X,Y)$ to $Y^p=f(X)$ that are contained in $\mathcal {O}_\infty ^{(p)}$ are constant.

As a consequence of this result, for any prime p, there are only finitely many numbers n, that are not powers of $\ell $ , for which $Y^n=f(X)$ has solutions in $F_\infty ^{(p)}$ . The methods used in proving the theorem are applied to another question of independent interest. Let K be a field of positive characteristic $\ell $ and A be the polynomial ring $K[T_1, \ldots , T_n]$ .

Theorem 1.3 (Theorem 4.1).

With the notation as above, let $f(X)$ be a polynomial with all of its coefficients and roots in K. Let $q\neq \ell $ be a prime number and assume that the following conditions are satisfied:

1. (1) $f(X)$ factorises into $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$ , where $a_0\in K$ , $a_1,\ldots , a_t$ are distinct elements in K, $n_1,\ldots , n_t$ are positive integers and $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Then any solution $(X,Y)\in A^2$ to

$$ \begin{align*} Y^{q}=f(X) \end{align*} $$

is constant, that is, X and Y are both in K.

It follows from this result that if $n>1$ is not a power of $\ell $ , then $X^n=f(X)$ does not have nonconstant solutions in A.

Organisation

In Section 2 we prove criteria for the constancy of solutions to $Y^n=f(X)$ in global function fields F. The main result in Section 2 is Theorem 2.4. In Section 3 we extend the results in Section 2 to prove the constancy of solutions to the above equation in $\mathbb {Z}_p$ -extensions of F. It is in this section that we prove the main result of the paper, that is, Theorem 3.2. In Section 4 we prove similar results for the polynomial rings over a field. Finally, in Section 5 we study the specific case where $f(X)=\sum _{i=1}^k (X+ir)^m$ .

2 Constancy of solutions to $Y^n=f(X)$ in a global function field

In this section we introduce basic notions and prove results about the solutions to certain Diophantine equations over global function fields. Throughout this section, $\ell $ is a prime number and A is an integral domain of characteristic $\ell $ with field of constants $\kappa $ . We introduce the notion of a discrete valuation on A.

Definition 2.1. A function $d:A\rightarrow \mathbb {Z}$ is said to be a discrete valuation if the following conditions are satisfied:

1. (1) the values taken by d are nonnegative;

2. (2) if $\mathbf {1}$ is the identity element of A, then $d(\mathbf {1})=0$ ;

3. (3) if $f,g\in A$ are nonzero elements, then $d(fg)=d(f)+d(g)$ ;

4. (4) $d(f+g)\leq \operatorname \max \{d(f),d(g)\}$ ,

5. (5) if $d(f)<d(g)$ , then $d(f+g)=d(f)$ .

Let $A_0$ be the subring of A consisting of all elements $a\in A$ for which $d(a)\leq 0$ . Given $f,g\in A$ , we say that f divides g if $fh=g$ for some $h\in A$ . It is clear that if f divides g then $d(f)\leq d(g)$ .

Lemma 2.2. Let q be a prime number such that $q\neq \ell $ , and A be an integral domain of characteristic $\ell $ equipped with a function d satisfying conditions (1)–(5) of Definition 2.1. Let $f,g,c\in A$ satisfy the equation

(2.1) $$ \begin{align}f^q-g^q=c.\end{align} $$

Then $d(f), d(g)\leq d(c)$ . In particular, f and g are contained in $A_0$ if c is contained in $A_0$ .

Proof. Suppose by way of contradiction that $d(f)>d(c)$ or $d(g)>d(c)$ . Assume first that $d(f)>d(c)$ . Set $e:=(g-f)$ . From (2.1), we find that e divides c. As a result, $d(e)\leq d(c)< d(f)$ . Hence by property (5) in Definition 2.1,

$$ \begin{align*}d(g)=d(f+e)=d(f).\end{align*} $$

Therefore, we have deduced that $d(g)>d(c)$ . Rewrite (2.1) as

$$ \begin{align*}(g+e)^q-g^q=c\end{align*} $$

and expand the left-hand side of this equation via the binomial expansion to give

$$ \begin{align*}qeg^{q-1}+{q\choose 2} e^2 g^{q-2}+\cdots +e^q=c.\end{align*} $$

Note that since $d(e)<d(g)$ , we find that, for all i such that $2\leq i\leq q$ ,

$$ \begin{align*}d\left({q\choose i}e^i g^{q-i}\right)< d(qeg^{q-1})\end{align*} $$

and therefore,

$$ \begin{align*}d(c)=d((g+e)^q-g^q)=d(qeg^{q-1})=(q-1)d(g).\end{align*} $$

This implies that $d(g)\leq d(c)$ , a contradiction. On the other hand, if we assume that $d(g)>d(c)$ (instead of assuming that $d(f)>d(c)$ ), the same argument applies.

We shall illustrate this result in various cases of interest. In this section we study Diophantine equations over global function fields F. Let $\ell $ be a prime number and denote by $\mathbb {F}_\ell $ the finite field with $\ell $ elements (that is, $\mathbb {Z}/\ell \mathbb {Z}$ ). Fix an algebraic closure $\bar {F}$ of F. Let $\kappa $ be the algebraic closure of $\mathbb {F}_\ell $ in F and let $\bar {\kappa }$ be the algebraic closure of $\kappa $ in $\bar {F}$ . Set $F'$ to denote the composite of F with $\bar {\kappa }$ .

Following [15, Ch. 5], a prime v of F is by definition the maximal ideal of a discrete valuation ring $\mathcal {O}_v\subset F$ with fraction field equal to F. A divisor of F is a finite linear combination $D=\sum _v n_v v$ of primes v. In this sum, the $n_v$ are all integers and the set of primes v for which $n_v\neq 0$ is referred to as the support of D. Given a function $g\in F$ , denote by $\operatorname {div}(g)$ the associated principal divisor. Note that any principal divisor has degree $0$ . Two divisors are considered equivalent if they differ by a principal divisor. The class group of F is the group of divisor classes of degree $0$ and has finite cardinality (see [15, Lemma 5.6]). Denote by $h_F$ the class number, that is, the number of elements in the class group. Given a natural number N, denote by $h_F[N]$ the cardinality of the N-torsion in the class group.

The field $F'$ is identified with the field of fractions of a projective algebraic curve $\mathfrak {X}$ over $\bar {\kappa }$ . A point $w\in \mathfrak {X}(\bar {\kappa })$ is also referred to as a prime of $F'$ , since it corresponds to a valuation ring $\mathcal {O}_w\subset F'$ with fraction field $F'$ . Given a prime w of $F'$ and a prime v of F, we say that w lies above (or divides) v if the natural inclusion of fields $F\hookrightarrow F'$ induces an inclusion of valuation rings $\mathcal {O}_v\hookrightarrow \mathcal {O}_w$ . Given a function $g\in F$ or $g\in F'$ , denote by $\operatorname {ord}_v(g)$ or $\operatorname {ord}_w(g)$ ) respectively the order of vanishing of g at v or w. We refer to $d_v(g):=-\operatorname {ord}_v(g)$ and $d_w(g):=-\operatorname {ord}_w(g)$ as the order of the pole of g at v and w, respectively. Given a finite and nonempty set of primes S of F, the ring of S-integers $\mathcal {O}_S$ consists of all functions $g\in F$ such that $d_v(g)\leq 0$ for all primes $v\notin S$ . Let $\bar {S}$ be the set of primes of $F'$ that lie above S. Let A denote the composite $\mathcal {O}_S\cdot \bar {\kappa }$ . A function $g\in A$ has the property that $d_w(g)\leq 0$ for all $w\notin \bar {S}$ . According to our conventions, $\mathcal {O}_F$ is the ring of S integers where $S:=\{P_\infty \}$ . Since $P_\infty $ is a prime of degree $1$ , it is totally inert in $F'$ . By abuse of notation, the single prime in $\bar {S}$ is also denoted by $P_\infty $ .

We list some basic properties of the function $d_w$ on A. The following result applies for any ring of $\bar {S}$ -integers.

Lemma 2.3. Let f and g be a functions in A and w be a point in $\mathfrak {X}(\bar {\kappa })$ . Then the following assertions hold:

1. (1) if $d_w(g)\leq 0$ for all $w\in \bar {S}$ , then g is a constant function;

2. (2) $d_w(fg)=d_w(f)+d_w(g)$ ;

3. (3) if $d_w(f)>d_w(g)$ , then $d_w(f+g)=d_w(f)$ .

Proof. Note that since g is contained in A, $d_w(g)\leq 0$ for all points $w\notin \bar {S}$ . Therefore, the assumption that $d_w(g)\leq 0$ implies that g has no poles and thus must be a constant function. This proves part (1).

Part (2) clearly follows from the relation $\operatorname {ord}_w(fg)=\operatorname {ord}_w(f)+\operatorname {ord}_w(g)$ .

For part (3), we note that $f+g=f(1+g/f)$ . Since it is assumed that $d_w(f)>d_w(g)$ , it follows that $g/f$ vanishes at w. As a result, $d_w(1+g/f)=0$ and thus

$$ \begin{align*}d_w(f+g)=d_w(f)+d_w(1+f/g)=d_w(f),\end{align*} $$

which proves the result.

Recall that $P_\infty $ is a prime of degree $1$ and $\mathcal {O}_F$ is the associated ring of integers in F.

Theorem 2.4. Let $\ell $ be a prime number and F be a global function field of characteristic $\ell $ . Let $\mathcal {O}_F$ be the ring of integers of F. Denote by $\kappa $ the field of constants of F. Let $f(X)$ be a polynomial with coefficients in $\kappa $ . Let $q\neq \ell $ be a prime number and let $k>0$ be the least integer such that $h_F[q^k]=h_F[q^{k-1}]$ . Assume that the following conditions are satisfied:

1. (1) $f(X)$ factorises into $f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$ where $a_0\in \kappa $ , $a_1,\ldots , a_t$ are distinct elements in $\kappa $ , $n_1,\ldots , n_t$ are positive integers and $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Then any solution $(X,Y)$ to

(2.2) $$ \begin{align} Y^{q^k}=f(X) \end{align} $$

for which $X,Y\in \mathcal {O}_F$ is constant, that is, X and Y are both in $\kappa $ .

Proof. Since the elements $a_1,\ldots , a_t$ are distinct elements of $\kappa $ , we find that for all $i, j$ such that $i\neq j$ , $(X-a_i)-(X-a_j)=a_j-a_i$ is a nonzero element of $\kappa $ . Therefore, for $i\neq j$ , the divisors $\operatorname {div}(X-a_i)$ and $\operatorname {div}(X-a_j)$ have disjoint supports.

From equation (2.2),

$$ \begin{align*} q^k \operatorname{div}(Y)=\sum_{i=1}^t n_i \operatorname{div}(X-a_i).\end{align*} $$

Since the divisors $\operatorname {div}(X-a_i)$ have disjoint supports for all i, there are divisors $D_i'$ such that $q^k D_i'=n_i\operatorname {div}(X-a_i)$ . Recall that it is assumed that there are two distinct indices i and j such that $q\nmid n_i$ and $q\nmid n_j$ . Without loss of generality, assume that $q\nmid n_1$ and $q\nmid n_2$ . Therefore, there exist divisors $D_1$ and $D_2$ such that $q^k D_i=\operatorname {div}(X-a_i)$ for $i=1,2$ . The divisor classes $[D_1]$ and $[D_2]$ in the class group are in the $q^k$ -torsion subgroup of the class group. Since $h_F[q^k]=h_F[q^{k-1}]$ , we find that $q^{k-1}D_i$ is principal for $i=1,2$ . Let f and g be functions in F such that

$$ \begin{align*}\operatorname{div}(f)=q^{k-1}D_1 \quad\text{and}\quad \operatorname{div}(g)=q^{k-1} D_2.\end{align*} $$

Thus $u_1f^q=(X-a_1)$ and $u_2 g^q=(X-a_2)$ , where $u_1$ and $u_2$ are contained in $\kappa $ . Note that since $(X-a_i)$ has no poles away from $\{P_\infty \}$ , the same is true for f and g, hence, $f,g\in \mathcal {O}_F$ . Setting $A:=\mathcal {O}_F\cdot \bar {\kappa }$ , we may replace f by $u_1^{1/q} f$ and g by $u_2^{1/q} g$ , and thus assume that $f^q=(X-a_1)$ and $g^q=(X-a_2)$ for some elements $f,g\in A$ . We find that $f^q-g^q=a_2-a_1$ is a nonzero element of $\kappa $ . The pair $(A,d_{P_\infty })$ satisfies properties (1)–(5) and therefore $d_{P_\infty }(f)=d_{P_\infty }(g)=0$ by Lemma 2.2. Therefore, by Lemma 2.3(1), f and g are both in $\kappa $ . Hence, $X=f^q+a_1$ is in $\kappa $ and thus so is Y.

Remark 2.5. We make the following observations.

• • Theorem 2.4 implies that $k=1$ if $q\nmid h_F$ .

• • If the roots $a_i$ are not contained in F, we may base-change F by an extension $\kappa '$ of $\kappa $ which is generated by the roots $a_i$ .

• • Suppose that $f(X)$ satisfies the conditions of Theorem 2.4. Since $q\nmid h_F$ for all but finitely many primes q, it follows that $Y^q=f(X)$ has no nonconstant solutions in F for all but finitely many primes q. In fact, it is easy to see that Theorem 2.4 implies that $Y^n=f(X)$ has no nonconstant solutions for all but finitely many natural numbers n.

3 Constancy of solutions to $Y^n=f(X)$ in the constant $\mathbb {Z}_p$ -extension of a function field

In this section we apply Theorem 2.4 to study questions motivated by Iwasawa theory. Given primes p and q (not necessarily distinct), let $h_n(p,q)$ denote $\# \operatorname {Cl}(F_n^{(p)})[q^\infty ]$ , the cardinality of the $q^\infty $ -torsion in the class group of $F_n^{(p)}$ .

Theorem 3.1 (Leitzel, Rosen).

Let p and q be (not necessarily distinct) prime numbers and F be a function field of characteristic $\ell $ . The following assertions hold:

1. (1) if p and q are distinct, then, as n goes to infinity, the quantity $h_n(p,q)$ is bounded;

2. (2) if p does not divide $h_F$ , then $h_n(p,p)=1$ for all n.

Proof. Part (1) follows from [15, Theorem 11.6]. For function fields of genus $1$ , the result was proved by Leitzel [9]. For part (2), see [15, Proposition 11.3].

Recall notation from the introduction. The prime $P_\infty $ is totally inert in $F_\infty ^{(p)}$ for any prime p. We set $\mathcal {O}_\infty ^{(p)}$ to denote the ring of integers of $F_\infty ^{(p)}$ , that is, the functions with no poles outside $\{P_\infty \}$ . The following is the main result of this paper.

Theorem 3.2. Let $\ell $ be a prime number and F be a global function field with field of constants $\kappa $ . Let p and q be prime numbers that are not necessarily distinct, and assume that $q\neq \ell $ . Let $f(X)$ be a polynomial with coefficients in $\kappa $ satisfying the conditions of Theorem 2.4. Then the following assertions hold.

1. (1) If p and q are distinct, then, for all sufficiently large numbers $k>0$ , the only solutions $(X,Y)$ to $Y^{q^k}=f(X)$ in $\mathcal {O}_\infty ^{(p)}$ are constant.

2. (2) If $p\nmid h_F$ , then the only solutions $(X,Y)$ to $Y^p=f(X)$ in $\mathcal {O}_\infty ^{(p)}$ are constant.

Proof. First, we consider the case where $p\ne q$ . From Theorem 3.1(1), $h_{n}(p,q)$ is bounded as n goes to infinity. Choose $k>0$ such that $q^k$ is larger than $\operatorname \max h_n(p,q)$ . From Theorem 2.4, $Y^{q^k}=f(X)$ has no nonconstant solutions in $\mathcal {O}_n^{(p)}$ for all n, and therefore, no nonconstant solutions in $\mathcal {O}_\infty ^{(p)}$ . Hence, there are no nonconstant solutions in $F_\infty $ .

Next, we consider the case where $p=q$ and $p\nmid h_F$ . Note that if $p\nmid h_F$ , then by Theorem 3.1(2), $ h_n(p,p)=1$ for all n. It follows from Theorem 2.4 that $Y^p=f(X)$ has no nonconstant solutions in $\mathcal {O}_n^{(p)}$ for all n, and therefore no nonconstant solutions in $\mathcal {O}_\infty ^{(p)}$ .

4 Constancy of solutions to $Y^n=f(X)$ in a polynomial ring in r-variables

In this section we study solutions to equations of the form $Y^n=f(X)$ in polynomial rings over a field. Let K be any field of characteristic $\ell>0$ and A be the polynomial ring $K[T_1, \ldots , T_r]$ . Given a polynomial g, let $d_i(g)$ be the degree of g viewed as a polynomial in $T_i$ over the subring $K[T_1, \ldots , T_{i-1}, T_{i+1}, \ldots , T_r]$ . The pair $(A,d_i)$ satisfies conditions (1)–(5) of Definition 2.1. The class group $\operatorname {Cl}(A)$ denotes the group of equivalence classes of Weil divisors. Since A is a unique factorisation domain, we have that $\operatorname {Cl}(A)=0$ .

Theorem 4.1. With the notation above, let $f(X)$ be a polynomial with all of its coefficients in K. Let $q\neq \ell $ be a prime number and assume that the following conditions are satisfied:

1. (1) $f(X)$ factorises into $f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$ where $a_0\in K$ , $a_1,\ldots , a_t$ are distinct elements in K, $n_1,\ldots , n_t$ are positive integers and $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Then any solution $(X,Y)\in A^2$ to

$$ \begin{align*} Y^{q}=f(X) \end{align*} $$

is constant, that is, X and Y are both in K.

Proof. Note that the algebraic closure of K in A is equal to K. We may as well replace K by its algebraic closure and assume without loss of generality that K is algebraically closed and that $q\nmid n_1$ and $q\nmid n_2$ . Since the class group of A is trivial, the same argument as in the proof of Theorem 2.4 shows that $(X-a_1)=f^q$ and $(X-a_2)=g^q$ for $f,g\in A$ . Therefore, $f^q-g^q=a_2-a_1$ , an element of K. Lemma 2.2 then implies that $d_i(f)=d_i(g)=0$ for all i, hence $f,g$ are both in K. The result follows.

5 Perfect powers that are sums of powers in arithmetic progressions

In this section we apply the results from previous sections to study the solutions of a Diophantine equation involving perfect powers in arithmetic progression:

$$ \begin{align*} Y^n=f(X):=(X+r)^m+(X+2r)^m+\cdots+ (X+dr)^m.\end{align*} $$

Here, $m, n, r, d$ are integers such that $m, n, d\geq 2$ and $r\geq 1$ . Let $\Delta $ denote the discriminant of $f(X)$ viewed as a polynomial with integral coefficients.

Theorem 5.1. Let F be a function field with characteristic $\ell \geq 5$ and field of functions $\kappa $ . Let $q\neq \ell $ be a prime. Assume that the following conditions are satisfied.

1. (1) All roots of $f(X)$ are contained in $\kappa $ .

2. (2) $\ell \nmid r$ .

3. (3) At least one of the following conditions are satisfied:

   1. (a) $\ell \nmid \Delta $ ;

   2. (b) $q>m$ and $d\not \equiv 0,\pm 1\,\mod {\ell }$ .

Let k be the minimal value such that $h_F[q^k]=h_F[q^{k-1}]$ . Then there are no nonconstant solutions $(X,Y)$ to

$$ \begin{align*}Y^{q^k}=f(X)=\sum_{i=1}^d (X+ir)^m\end{align*} $$

in $\mathcal {O}_F^2$ .

Proof. With the notation from the statement of Theorem 2.4, we write

$$ \begin{align*}f(X)=a_0\prod_{j=1}^t (X-a_i)^{n_i},\end{align*} $$

where $a_1,\ldots , a_t$ are distinct elements of $\kappa $ . The result follows from Theorem 2.4 provided that:

1. (1) $t\geq 2$ ;

2. (2) at least two of the exponents $n_i$ are not divisible by q.

Note that if $\ell \nmid \Delta $ , then all roots of $f(X)$ are distinct in $\kappa $ . Hence, $n_i=1$ for all i and $t=d\geq 2$ . In particular, both of the above conditions are satisfied.

On the other hand, assume that $q>m$ . Clearly, all values $n_i$ are less than or equal to $\operatorname {deg} f(X)\leq m$ , and since $q>m$ , it follows that $q\nmid n_i$ for all i. It suffices to check that $t\geq 2$ if $d\not \equiv 0,\pm 1 \,\mod {\ell }$ . Suppose not, then $f(X)$ is of the form $d(X+a)^m$ , for some $a\in \kappa $ . Expanding $f(X)=\sum _{i=1}^d (X+ir)^m$ ,

$$ \begin{align*}\begin{split} \sum_{i=1}^d (X+ir)^m &= \sum_{i=1}^d \sum_{j=0}^m {m\choose j} i^{j} r^{j} X^{m-j}\\ &= \sum_{j=0}^m {m\choose j}r^{j}\bigg( \sum_{i=1}^d i^{j}\bigg)X^{m-j}\\ &=d X^m+mr\bigg(\frac{d(d+1)}{2}\bigg)X^{m-1}+{m\choose 2}r^2\bigg(\frac{d(d+1)(2d+1)}{6}\bigg)X^{m-2}+\cdots. \end{split}\end{align*} $$

Since $f(X)=d(X+a)^m$ and $\ell \nmid d$ , we find that

$$ \begin{align*}a^j=r^j \bigg( \frac{1}{d}\sum_{i=1}^d i^{\,j}\bigg)\end{align*} $$

for all values of j. In particular,

$$ \begin{align*}a=r\bigg(\frac{(d+1)}{2}\bigg) \quad\text{and}\quad a^2=r^2\bigg(\frac{(d+1)(2d+1)}{6}\bigg).\end{align*} $$

We thus arrive at the relation

(5.1) $$ \begin{align}a^2=r^2\bigg(\frac{(d+1)}{2}\bigg)^2=r^2\bigg(\frac{(d+1)(2d+1)}{6}\bigg).\end{align} $$

The relation holds in $\mathbb {Z}/\ell \mathbb {Z}$ . Since $\ell \nmid r$ and $d\not \equiv -1\,\mod {\ell }$ by assumption, relation (5.1) gives

$$ \begin{align*}\frac{(d+1)}{4}=\frac{2d+1}{6}.\end{align*} $$

This is not possible since it is assumed that $d\not \equiv 1\,\mod {\ell }$ . Thus, Theorem 2.4 applies to give the result.

Theorem 5.2. Let F be a function field with characteristic $\ell \geq 5$ and field of functions $\kappa $ . Let $q\neq \ell $ be a prime. Assume that the following conditions are satisfied.

1. (1) All roots of $f(X)$ are contained in $\kappa $ .

2. (2) $\ell \nmid r$ .

3. (3) At least one of the following conditions are satisfied:

   1. (a) $\ell \nmid \Delta $ ;

   2. (b) $q>m$ and $d\not \equiv 0,\pm 1\,\mod {\ell }$ .

Let p be any prime number. Then the following assertions hold.

1. (i) If $p\neq q$ , then for all large enough values of $k>0$ , there are no nonconstant solutions to $Y^{q^k}=f(X)$ in $\mathcal {O}_\infty ^{(p)}$ .

2. (ii) If $p=q$ and $p\nmid h_F$ , then there are no nonconstant solutions to $Y^p=f(X)$ in $\mathcal {O}_\infty ^{(p)}$ .

Proof. It follows from the proof of Theorem 5.1 that the conditions of Theorem 3.2 are satisfied, and thus the result follows.

Theorem 5.3. Let K be a field of characteristic $\ell \geq 5$ and let A be the polynomial ring $K[T_1, \ldots , T_r]$ . Let $q\neq \ell $ be a prime. Assume that the following conditions are satisfied.

1. (1) All roots of $f(X)$ are contained in K.

2. (2) $\ell \nmid r$ .

3. (3) At least one of the following conditions are satisfied:

   1. (a) $\ell \nmid \Delta $ ;

   2. (b) $q>m$ and $d\not \equiv 0,\pm 1\,\mod {\ell }$ .

Then any solution $(X,Y)\in A^2$ to

$$ \begin{align*} Y^{q}=f(X) \end{align*} $$

is constant, that is, X and Y are both in K.

Proof. It follows from the proof of Theorem 5.1 that the conditions of Theorem 4.1 are satisfied. The result thus follows from Theorem 4.1.