Article contents
HEAT KERNEL METHOD FOR THE LEVI-CIVITÁ EQUATION IN DISTRIBUTIONS AND HYPERFUNCTIONS
Published online by Cambridge University Press: 04 May 2015
Abstract
Let 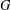 $G$ be a commutative group and
$G$ be a commutative group and 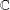 $\mathbb{C}$ the field of complex numbers,
$\mathbb{C}$ the field of complex numbers, 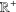 $\mathbb{R}^{+}$ the set of positive real numbers and
$\mathbb{R}^{+}$ the set of positive real numbers and 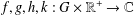 $f,g,h,k:G\times \mathbb{R}^{+}\rightarrow \mathbb{C}$. In this paper, we first consider the Levi-Civitá functional inequality
$f,g,h,k:G\times \mathbb{R}^{+}\rightarrow \mathbb{C}$. In this paper, we first consider the Levi-Civitá functional inequality 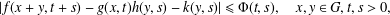 $$\begin{eqnarray}\displaystyle |f(x+y,t+s)-g(x,t)h(y,s)-k(y,s)|\leq {\rm\Phi}(t,s),\quad x,y\in G,t,s>0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |f(x+y,t+s)-g(x,t)h(y,s)-k(y,s)|\leq {\rm\Phi}(t,s),\quad x,y\in G,t,s>0, & & \displaystyle \nonumber\end{eqnarray}$$ ${\rm\Phi}:\mathbb{R}^{+}\times \mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$ is a symmetric decreasing function in the sense that
${\rm\Phi}:\mathbb{R}^{+}\times \mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$ is a symmetric decreasing function in the sense that 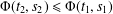 ${\rm\Phi}(t_{2},s_{2})\leq {\rm\Phi}(t_{1},s_{1})$ for all
${\rm\Phi}(t_{2},s_{2})\leq {\rm\Phi}(t_{1},s_{1})$ for all 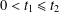 $0<t_{1}\leq t_{2}$ and
$0<t_{1}\leq t_{2}$ and 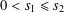 $0<s_{1}\leq s_{2}$. As an application, we solve the Hyers–Ulam stability problem of the Levi-Civitá functional equation
$0<s_{1}\leq s_{2}$. As an application, we solve the Hyers–Ulam stability problem of the Levi-Civitá functional equation 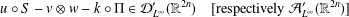 $$\begin{eqnarray}\displaystyle u\circ S-v\otimes w-k\circ {\rm\Pi}\in {\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})\quad [\text{respectively}\;{\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})] & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u\circ S-v\otimes w-k\circ {\rm\Pi}\in {\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})\quad [\text{respectively}\;{\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})] & & \displaystyle \nonumber\end{eqnarray}$$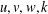 $u,v,w,k$ are Gelfand hyperfunctions,
$u,v,w,k$ are Gelfand hyperfunctions, 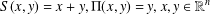 $S(x,y)=x+y,{\rm\Pi}(x,y)=y,x,y\in \mathbb{R}^{n}$, and
$S(x,y)=x+y,{\rm\Pi}(x,y)=y,x,y\in \mathbb{R}^{n}$, and  $\circ$,
$\circ$,  $\otimes$,
$\otimes$,  ${\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$ and
${\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$ and  ${\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$ denote pullback, tensor product and the spaces of bounded distributions and bounded hyperfunctions, respectively.
${\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$ denote pullback, tensor product and the spaces of bounded distributions and bounded hyperfunctions, respectively.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by


