Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Han, Q.
and
Yuan, P.
2018.
A note on Jeśmanowicz’ conjecture.
Acta Mathematica Hungarica,
Vol. 156,
Issue. 1,
p.
220.
Le, Maohua
and
Soydan, Gökhan
2020.
An application of Baker’s method to the Jeśmanowicz’ conjecture on primitive Pythagorean triples.
Periodica Mathematica Hungarica,
Vol. 80,
Issue. 1,
p.
74.
Yan, Xiao-Hui
2020.
The Diophantine equation (m2 + n2)x + (2mn)y = (m + n)2z.
International Journal of Number Theory,
Vol. 16,
Issue. 08,
p.
1701.
Alan, Murat
2020.
On the Exponential Diophantine Equation $$(m^2+m+1)^x+m^y=(m+1)^z $$.
Mediterranean Journal of Mathematics,
Vol. 17,
Issue. 6,
Dimabayao, Jerome T.
2021.
Jeśmanowicz’ conjecture for polynomials.
Periodica Mathematica Hungarica,
Vol. 82,
Issue. 1,
p.
29.
Alan, Murat
2021.
On the exponential Diophantine equation mx
+(m+1)
y
=(1+m+m
2)
z
.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 29,
Issue. 3,
p.
23.
Ghadermarzi, Amir
2022.
On the Exceptional Solutions of Jeśmanowicz’ Conjecture.
Bulletin of the Iranian Mathematical Society,
Vol. 48,
Issue. 3,
p.
933.
Yang, Hai
and
Fu, Ruiqin
2022.
A Further Note on Jeśmanowicz’ Conjecture Concerning Primitive Pythagorean Triples.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 2,
Feng, Cheng
and
Luo, Jiagui
2022.
On the exponential Diophantine equation $ \left(\frac{q^{2l}-p^{2k}}{2}n\right)^x+(p^kq^ln)^y = \left(\frac{q^{2l}+p^{2k}}{2}n\right)^z $.
AIMS Mathematics,
Vol. 7,
Issue. 5,
p.
8609.
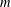 $m$ and
$m$ and  $n$ with
$n$ with 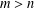 $m>n$,
$m>n$, 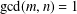 $\gcd (m,n)=1$ and
$\gcd (m,n)=1$ and 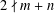 $2\nmid m+n$, the Diophantine equation
$2\nmid m+n$, the Diophantine equation  $(m^{2}-n^{2})^{x}+(2mn)^{y}=(m^{2}+n^{2})^{z}$ has only the positive integer solution
$(m^{2}-n^{2})^{x}+(2mn)^{y}=(m^{2}+n^{2})^{z}$ has only the positive integer solution  $(x,y,z)=(2,2,2)$. In this paper, we prove the conjecture if
$(x,y,z)=(2,2,2)$. In this paper, we prove the conjecture if 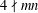 $4\nmid mn$ and
$4\nmid mn$ and 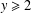 $y\geq 2$.
$y\geq 2$.