Published online by Cambridge University Press: 13 May 2015
For triangular arrays 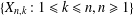 $\{X_{n,k}:1\leqslant k\leqslant n,n\geqslant 1\}$ of upper extended negatively dependent random variables weakly mean dominated by a random variable
$\{X_{n,k}:1\leqslant k\leqslant n,n\geqslant 1\}$ of upper extended negatively dependent random variables weakly mean dominated by a random variable 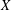 $X$ and sequences
$X$ and sequences  $\{b_{n}\}$ of positive constants, conditions are given to guarantee an almost sure finite upper bound to
$\{b_{n}\}$ of positive constants, conditions are given to guarantee an almost sure finite upper bound to 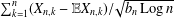 $\sum _{k=1}^{n}(X_{n,k}-\mathbb{E}X_{n,k})/\!\sqrt{b_{n}\,\text{Log}\,n}$, where
$\sum _{k=1}^{n}(X_{n,k}-\mathbb{E}X_{n,k})/\!\sqrt{b_{n}\,\text{Log}\,n}$, where 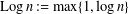 $\text{Log}\,n:=\max \{1,\log n\}$, thus getting control over the limiting rate in terms of the prescribed sequence
$\text{Log}\,n:=\max \{1,\log n\}$, thus getting control over the limiting rate in terms of the prescribed sequence 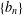 $\{b_{n}\}$ and permitting us to weaken or strengthen the assumptions on the random variables.
$\{b_{n}\}$ and permitting us to weaken or strengthen the assumptions on the random variables.