Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:04:53.596Z Has data issue: false hasContentIssue false
  • English
  • Français

NONREGULAR GRAPHS WITH MINIMAL TOTAL IRREGULARITY

Part of: Graph theory

Published online by Cambridge University Press:  29 April 2015

HOSAM ABDO  and
DARKO DIMITROV
HOSAM ABDO
Affiliation:
Department of Mathematics and Computer Science, Freie Universität Berlin, Takustraße 9, D-14195 Berlin, Germany email abdo@mi.fu-berlin.de
DARKO DIMITROV*
Affiliation:
Department of Engineering Sciences I, Hochschule für Technik und Wirtschaft Berlin, Wilhelminenhofstraße 75A, D-12459 Berlin, Germany email darko.dimitrov11@gmail.com
*
✉darko.dimitrov11@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The total irregularity of a simple undirected graph 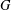$G$ is defined as 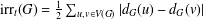$\text{irr}_{t}(G)=\frac{1}{2}\sum _{u,v\in V(G)}|d_{G}(u)-d_{G}(v)|$, where 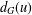$d_{G}(u)$ denotes the degree of a vertex 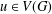$u\in V(G)$. Obviously, 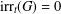$\text{irr}_{t}(G)=0$ if and only if 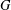$G$ is regular. Here, we characterise the nonregular graphs with minimal total irregularity and thereby resolve the recent conjecture by Zhu et al. [‘The minimal total irregularity of graphs’, Preprint, 2014, arXiv:1404.0931v1 ] about the lower bound on the minimal total irregularity of nonregular connected graphs. We show that the conjectured lower bound of 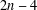$2n-4$ is attained only if nonregular connected graphs of even order are considered, while the sharp lower bound of 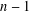$n-1$ is attained by graphs of odd order. We also characterise the nonregular graphs with the second and the third smallest total irregularity.

Keywords

total irregularityextremal graphs

MSC classification

Primary: 05C07: Vertex degrees
Secondary: 05C35: Extremal problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 1 - 10
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abdo, H., Brandt, S. and Dimitrov, D., ‘The total irregularity of a graph’, Discrete Math. Theor. Comput. Sci. 16 (2014), 201–206.Google Scholar
Abdo, H., Cohen, N. and Dimitrov, D., ‘Graphs with maximal irregularity’, Filomat 26(7) (2014), 1315–1322.CrossRefGoogle Scholar
Alavi, Y., Boals, A., Chartrand, G., Erdős, P. and Oellermann, O. R., ‘k-path irregular graphs’, Congr. Numer. 65 (1988), 201–210.Google Scholar
Alavi, Y., Chartrand, G., Chung, F. R. K., Erdős, P., Graham, R. L. and Oellermann, O. R., ‘Highly irregular graphs’, J. Graph Theory 11 (1987), 235–249.CrossRefGoogle Scholar
Albertson, M. O., ‘The irregularity of a graph’, Ars Combin. 46 (1997), 219–225.Google Scholar
Bell, F. K., ‘A note on the irregularity of graphs’, Linear Algebra Appl. 161 (1992), 45–54.CrossRefGoogle Scholar
Berge, C., Graphs and Hypergraphs, 2nd edn. (North-Holland, Amsterdam, 1976).Google Scholar
Chartrand, G., Erdős, P. and Oellermann, O. R., ‘How to define an irregular graph’, College Math. J. 19 (1988), 36–42.CrossRefGoogle Scholar
Chartrand, G., Holbert, K. S., Oellermann, O. R. and Swart, H. C., ‘F-degrees in graphs’, Ars Combin. 24 (1987), 133–148.Google Scholar
Chartrand, G., Jacobson, M. S., Lehel, J., Oellermann, O. R., Ruiz, S. and Saba, F., ‘Irregular networks’, Congr. Numer. 64 (1988), 197–210.Google Scholar
Collatz, L. and Sinogowitz, U., ‘Spektren endlicher Graphen’, Abh. Math. Semin. Univ. Hambg. 21 (1957), 63–77.Google Scholar
Dimitrov, D. and Škrekovski, R., ‘Comparing the irregularity and the total irregularity of graphs’, Ars Math. Contemp. 9 (2015), 45–50.CrossRefGoogle Scholar
Erdős, P. and Gallai, T., ‘Graphs with prescribed degrees of vertices’, Mat. Lapok (N.S.) 11 (1960), 264–274; (in Hungarian).Google Scholar
Hansen, P. and Mélot, H., ‘Variable neighborhood search for extremal graphs 9. Bounding the irregularity of a graph’, DIMACS Ser. Discrete Math. Theor. Comput. Sci. 69 (2005), 253–264.CrossRefGoogle Scholar
Henning, M. A. and Rautenbach, D., ‘On the irregularity of bipartite graphs’, Discrete Math. 307 (2007), 1467–1472.CrossRefGoogle Scholar
Tripathi, A. and Vijay, S., ‘A note on a theorem of Erdős & Gallai’, Discrete Math. 265 (2003), 417–420.CrossRefGoogle Scholar
You, L., Yang, J. and You, Z., ‘The maximal total irregularity of bicyclic graphs’, J. Appl. Math. 2014 (2014), 785084, 9 pages; doi:10.1155/2014/785084.CrossRefGoogle Scholar
You, L., Yang, J. and You, Z., ‘The maximal total irregularity of unicyclic graphs’, Ars Combin. 114 (2014), 153–160.Google Scholar
Zhu, Y., You, L. and Yang, J., ‘The minimal total irregularity of graphs’, Preprint, 2014, arXiv:1404.0931v1.CrossRefGoogle Scholar