Article contents
A NOTE ON REGULAR SETS IN CAYLEY GRAPHS
Published online by Cambridge University Press: 09 February 2023
Abstract
A subset R of the vertex set of a graph 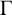 $\Gamma $ is said to be
$\Gamma $ is said to be 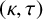 $(\kappa ,\tau )$-regular if R induces a
$(\kappa ,\tau )$-regular if R induces a 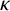 $\kappa $-regular subgraph and every vertex outside R is adjacent to exactly
$\kappa $-regular subgraph and every vertex outside R is adjacent to exactly 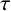 $\tau $ vertices in R. In particular, if R is a
$\tau $ vertices in R. In particular, if R is a 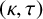 $(\kappa ,\tau )$-regular set of some Cayley graph on a finite group G, then R is called a
$(\kappa ,\tau )$-regular set of some Cayley graph on a finite group G, then R is called a 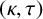 $(\kappa ,\tau )$-regular set of G. Let H be a nontrivial normal subgroup of G, and
$(\kappa ,\tau )$-regular set of G. Let H be a nontrivial normal subgroup of G, and 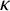 $\kappa $ and
$\kappa $ and 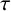 $\tau $ a pair of integers satisfying
$\tau $ a pair of integers satisfying 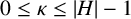 $0\leq \kappa \leq |H|-1$,
$0\leq \kappa \leq |H|-1$, 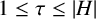 $1\leq \tau \leq |H|$ and
$1\leq \tau \leq |H|$ and 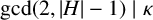 $\gcd (2,|H|-1)\mid \kappa $. It is proved that (i) if
$\gcd (2,|H|-1)\mid \kappa $. It is proved that (i) if 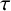 $\tau $ is even, then H is a
$\tau $ is even, then H is a 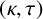 $(\kappa ,\tau )$-regular set of G; (ii) if
$(\kappa ,\tau )$-regular set of G; (ii) if 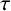 $\tau $ is odd, then H is a
$\tau $ is odd, then H is a 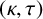 $(\kappa ,\tau )$-regular set of G if and only if it is a
$(\kappa ,\tau )$-regular set of G if and only if it is a 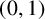 $(0,1)$-regular set of G.
$(0,1)$-regular set of G.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the Natural Science Foundation of Chongqing (CSTB2022NSCQ- MSX1054) and the Foundation of Chongqing Normal University (21XLB006).
References
- 4
- Cited by


