No CrossRef data available.
Published online by Cambridge University Press: 16 June 2015
If the centre of a group 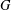 $G$ is trivial, then so is the centre of its automorphism group. We study the structure of the centre of the automorphism group of a group
$G$ is trivial, then so is the centre of its automorphism group. We study the structure of the centre of the automorphism group of a group 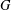 $G$ when the centre of
$G$ when the centre of 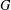 $G$ is a cyclic group. In particular, it is shown that the exponent of
$G$ is a cyclic group. In particular, it is shown that the exponent of 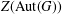 $Z(\text{Aut}(G))$ is less than or equal to the exponent of
$Z(\text{Aut}(G))$ is less than or equal to the exponent of 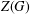 $Z(G)$ in this case.
$Z(G)$ in this case.