Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T05:55:54.615Z Has data issue: false hasContentIssue false
  • English
  • Français

REALISABLE SETS OF CATENARY DEGREES OF NUMERICAL MONOIDS

Part of: Semigroups

Published online by Cambridge University Press:  04 December 2017

CHRISTOPHER O’NEILL  and
ROBERTO PELAYO
CHRISTOPHER O’NEILL*
Affiliation:
Mathematics Department, University of California, Davis, One Shields Ave, Davis, CA 95616, USA email coneill@math.ucdavis.edu
ROBERTO PELAYO
Affiliation:
Mathematics Department, University of Hawai‘i at Hilo, Hilo, HI 96720, USA email robertop@hawaii.edu
*
✉coneill@math.ucdavis.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

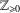The catenary degree is an invariant that measures the distance between factorisations of elements within an atomic monoid. In this paper, we classify which finite subsets of $\mathbb{Z}_{\geq 0}$ occur as the set of catenary degrees of a numerical monoid (that is, a co-finite, additive submonoid of 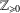$\mathbb{Z}_{\geq 0}$). In particular, we show that, with one exception, every finite subset of 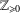$\mathbb{Z}_{\geq 0}$ that can possibly occur as the set of catenary degrees of some atomic monoid is actually achieved by a numerical monoid.

Keywords

catenary degreeatomic monoidnumerical monoidnonunique factorisation

MSC classification

Primary: 20M13: Arithmetic theory of monoids
Secondary: 20M14: Commutative semigroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 240 - 245
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Bullejos, M. and García-Sánchez, P., ‘Minimal presentations for monoids with the ascending chain condition on principal ideals’, Semigroup Forum 85(1) (2012), 185–190.Google Scholar
Chapman, S., García-Sánchez, P., Llena, D., Ponomarenko, V. and Rosales, J., ‘The catenary and tame degree in finitely generated commutative cancellative monoids’, Manuscripta Math. 120(3) (2006), 253–264.CrossRefGoogle Scholar
Colton, S. and Kaplan, N., ‘The realization problem for delta sets of numerical semigroups’, Preprint, 2015, arXiv:1503.08496.Google Scholar
Delgado, M., García-Sánchez, P. and Morais, J., ‘NumericalSgps, A package for numerical semigroups’, Version 1.1.0, 2017, GAP package, https://gap-packages.github.io/numericalsgps/.Google Scholar
Fan, Y. and Geroldinger, A., ‘Minimal relations and catenary degrees in Krull monoids’, Preprint, 2016, arXiv:1603.06356.Google Scholar
García-Sánchez, P., Llena, D. and Moscariello, A., ‘‘Delta sets for numerical semigroups with embedding dimension three’’, Forum Math. to appear, arXiv:1504.02116.Google Scholar
García-Sánchez, P., Llena, D. and Moscariello, A., ‘‘Delta sets for symmetric numerical semigroups with embedding dimension three’’, Aequationes Math. 91(3) (2017), 579–600.Google Scholar
García-Sánchez, P., Ojeda, I., Sánchez, R. and Navarro, A., ‘‘Factorization invariants in half-factorial affine semigroups’’, Internat. J. Algebra Comput. 23(1) (2013), 111–122.Google Scholar
Geroldinger, A. and Halter-Koch, F., Nonunique Factorization: Algebraic, Combinatorial and Analytic Theory, Pure and Applied Mathematics, 278 (Chapman & Hall/CRC, Boca Raton, FL, 2006).Google Scholar
Geroldinger, A. and Schmid, W., ‘A realization theorem for sets of distances’, J. Algebra 481 (2017), 188–198.Google Scholar
O’Neill, C., Ponomarenko, V., Tate, R. and Webb, G., ‘On the set of catenary degrees of finitely generated cancellative commutative monoids’, Internat. J. Algebra Comput. 26(3) (2016), 565–576.Google Scholar
Rosales, J. and García-Sánchez, P., Numerical Semigroups, Developments in Mathematics, 20 (Springer, New York, NY, 2009).Google Scholar