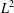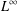Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Luan, Tran Nhat
2021.
An inverse time-fractional diffusion problem with Robin boundary condition in two layers spherical domain.
Computational and Applied Mathematics,
Vol. 40,
Issue. 8,