Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:19:26.839Z Has data issue: false hasContentIssue false
  • English
  • Français

SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT

Part of: Surfaces and higher-dimensional varieties Difference equations Difference and functional equations Birational geometry Complex dynamical systems Curves

Published online by Cambridge University Press:  05 October 2020

GIORGIO GUBBIOTTI Open the ORCID record for GIORGIO GUBBIOTTI [Opens in a new window]  and
NALINI JOSHI Open the ORCID record for NALINI JOSHI [Opens in a new window]
GIORGIO GUBBIOTTI*
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW2006, Australia
NALINI JOSHI
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW2006, Australia e-mail: nalini.joshi@sydney.edu.au
*
e-mail: giorgio.gubbiotti@sydney.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We compactify and regularise the space of initial values of a planar map with a quartic invariant and use this construction to prove its integrability in the sense of algebraic entropy. The system has certain unusual properties, including a sequence of points of indeterminacy in 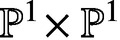$\mathbb {P}^{1}\!\times \mathbb {P}^{1}$ . These indeterminacy points lie on a singular fibre of the mapping to a corresponding QRT system and provide the existence of a one-parameter family of special solutions.

Keywords

space of initial valuesintegrabilityKahan discretisationresolution of indeterminacies

MSC classification

Primary: 14E05: Rational and birational maps
Secondary: 14E15: Global theory and resolution of singularities 14H70: Relationships with integrable systems 14J17: Singularities 37F10: Polynomials; rational maps; entire and meromorphic functions 39A10: Difference equations, additive
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 438 - 449
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research reported in this paper was supported by the Australian Laureate Fellowship #FL120100094 and Discovery Project #DP190101838 from the Australian Research Council.

References

Bellon, M. and Viallet, C.-M., ‘Algebraic entropy’, Comm. Math. Phys. 204 (1999), 425–437.CrossRefGoogle Scholar
Carstea, A. S. and Takenawa, T., ‘Space of initial conditions and geometry of two 4-dimensional discrete Painlevé equations’, J. Phys. A: Math. Theor. 52 (2019), 275201.CrossRefGoogle Scholar
Celledoni, E., McLachlan, R. I., McLaren, D. I., Owren, B. and Quispel, G. R. W., ‘Integrability properties of Kahan’s method’, J. Phys. A: Math. Theor. 47(36) (2014), 365202.CrossRefGoogle Scholar
Celledoni, E., McLachlan, R. I., McLaren, D. I., Owren, B. and Quispel, G. R. W., ‘Two classes of quadratic vector fields for which the Kahan discretization is integrable’, MI Lecture Notes 74 (2017), 60–62.Google Scholar
Diller, J. and Favre, C., ‘Dynamics of bimeromorphic maps of surfaces’, Amer. J. Math. 123(6) (2001), 1135–1169.CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer, New York, 1977).CrossRefGoogle Scholar
Hay, M., Howes, P., Nakazono, N. and Shi, Y., ‘A systematic approach to reductions of type-Q ABS equations’, J. Phys. A: Math. Theor. 48 (2015), 095201.CrossRefGoogle Scholar
Hietarinta, J., Joshi, N. and Nijhoff, F., Discrete Systems and Integrability, Cambridge Texts in Applied Mathematics, 54 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Hitchin, N. J., Manton, N. S. and Murray, M. K., ‘Symmetric monopoles’, Nonlinearity 8 (1995), 661–692.CrossRefGoogle Scholar
Joshi, N., Discrete Painlevé Equations , CBMS Regional Conference Series in Mathematics, 131 (American Mathematical Society, Providence, RI, 2019).Google Scholar
Kahan, W., ‘Unconventional numerical methods for trajectory calculations’. Unpublished lecture notes, 1993.Google Scholar
Kajiwara, K., Noumi, M. and Yamada, Y., ‘Geometric aspects of Painlevé equations’, J. Phys. A 50 (2017), 073001.CrossRefGoogle Scholar
Kimura, K. and Hirota, R., ‘Discretization of the Lagrange top’, J. Phys. Soc. Japan 69 (2000), 3193–3199.CrossRefGoogle Scholar
Petrera, M., Pfadler, A. and Suris, Yu. B., ‘On integrability of Hirota–Kimura type discretizations’, Regul. Chaot. Dyn. 16 (2011), 245–289.CrossRefGoogle Scholar
Petrera, M. and Zander, R., ‘New classes of quadratic vector fields admitting integral-preserving Kahan–Hirota–Kimura discretizations’, J. Phys. A: Math. Theor. 50 (2017), 205203.CrossRefGoogle Scholar
Quispel, G. R. W., Roberts, J. A. G. and Thompson, C. J., ‘Integrable mappings and soliton equations’, Phys. Lett. A 126 (1988), 419.CrossRefGoogle Scholar
Quispel, G. R. W., Roberts, J. A. G. and Thompson, C. J., ‘Integrable mappings and soliton equations II’, Phys. D 34(1) (1989), 183–192.CrossRefGoogle Scholar
Sakai, H., ‘Rational surfaces associated with affine root systems and geometry of the Painlevé equations’, Comm. Math. Phys. 220(1) (2001), 165–229.CrossRefGoogle Scholar
Takenawa, T., ‘Algebraic entropy and the space of initial values for discrete dynamical systems’, J. Phys. A Math. Gen. 34 (2001), 10533.CrossRefGoogle Scholar
Takenawa, T., Eguchi, M., Grammaticos, B., Ohta, Y., Ramani, A. and Satsuma, J., ‘The space of initial conditions for linearizable mappings’, Nonlinearity 16 (2003), 457–477.CrossRefGoogle Scholar
Tsuda, T., ‘Integrable mappings via rational elliptic surfaces’, J. Phys. A: Math. Gen. 37 (2004), 2721.CrossRefGoogle Scholar
van der Kamp, P. H., Celledoni, E., McLachlan, R. I., McLaren, D. I., Owren, B. and Quispel, G. R. W., ‘Three classes of quadratic vector fields for which the Kahan discretisation is the root of a generalised Manin transformation’, J. Phys. A: Math. Theor. 52 (2019), 045204.CrossRefGoogle Scholar
Zander, R., ‘On the singularity structure of Kahan discretizations of a class of quadratic vector fields’, Preprint, arXiv:2003.01659, 2020.Google Scholar