Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T21:23:59.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Automaticity and Invariant Measures of Linear Cellular Automata

Part of: Sequences and sets Topological dynamics

Published online by Cambridge University Press:  05 September 2019

Eric Rowland  and
Reem Yassawi
Eric Rowland
Affiliation:
Department of Mathematics, Hofstra University, Hempstead, NY, USA Email: eric.rowland@hofstra.edu
Reem Yassawi
Affiliation:
Institut Camille Jordan, Université Lyon-1, France School of Mathematics and Statistics, Open University, UK Email: reem.yassawi@open.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that spacetime diagrams of linear cellular automata 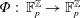$\unicode[STIX]{x1D6F7}:\,\mathbb{F}_{p}^{\mathbb{Z}}\rightarrow \mathbb{F}_{p}^{\mathbb{Z}}$ with 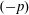$(-p)$-automatic initial conditions are automatic. This extends existing results on initial conditions that are eventually constant. Each automatic spacetime diagram defines a 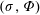$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F7})$-invariant subset of 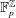$\mathbb{F}_{p}^{\mathbb{Z}}$, where $\unicode[STIX]{x1D70E}$ is the left shift map, and if the initial condition is not eventually periodic, then this invariant set is nontrivial. For the Ledrappier cellular automaton we construct a family of nontrivial $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F7})$-invariant measures on $\mathbb{F}_{3}^{\mathbb{Z}}$. Finally, given a linear cellular automaton 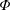$\unicode[STIX]{x1D6F7}$, we construct a nontrivial 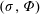$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F7})$-invariant measure on $\mathbb{F}_{p}^{\mathbb{Z}}$ for all but finitely many 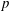$p$.

Keywords

linear cellular automatainvariant measureautomatic sequenceChristol’s theorem

MSC classification

Primary: 11B85: Automata sequences
Secondary: 37B15: Cellular automata
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1691 - 1726
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under the Grant Agreement No 648132.

References

Adamczewski, B. and Bell, J. P., Diagonalization and rationalization of algebraic Laurent series. Ann. Sci. Éc. Norm. Supér. (4) 46(2013), 963–1004. https://doi.org/10.24033/asens.2207CrossRefGoogle Scholar
Allouche, J.-P. and Berthé, V., Triangle de Pascal, complexité et automates. Journées Montoises (Mons, 1994). Bull. Belg. Math. Soc. Simon Stevin 4(1997), 1–23.CrossRefGoogle Scholar
Allouche, J.-P., Deshouillers, J.-M., Kamae, T., and Koyanagi, T., Automata, algebraicity and distribution of sequences of powers. Ann. Inst. Fourier (Grenoble) 51(2001), 687–705.CrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., Automatic sequences: Theory, applications, generalizations. Cambridge University Press, Cambridge, 2003. https://doi.org/10.1017/CBO9780511546563CrossRefGoogle Scholar
Allouche, J.-P., von Haeseler, F., Lange, E., Petersen, A., and Skordev, G., Linear cellular automata and automatic sequences. Cellular automata (Gießen, 1996). Parallel Comput. 23(1997), 1577–1592. https://doi.org/10.1016/S0167-8191(97)00074-4CrossRefGoogle Scholar
Allouche, J.-P., von Haeseler, F., Peitgen, H.-O., Petersen, A., and Skordev, G., Automaticity of double sequences generated by one-dimensional linear cellular automata. Theoret. Comput. Sci. 188(1997), 195–209. https://doi.org/10.1016/S0304-3975(96)00298-8CrossRefGoogle Scholar
Allouche, J.-P., von Haeseler, F., Peitgen, H.-O., and Skordev, G., Linear cellular automata, finite automata and Pascal’s triangle. Discrete Appl. Math. 66(1996), 1–22. https://doi.org/10.1016/0166-218X(94)00132-WCrossRefGoogle Scholar
Aparicio Monforte, A. and Kauers, M., Formal Laurent series in several variables. Expo. Math. 31(2013), 350–367. https://doi.org/10.1016/j.exmath.2013.01.004CrossRefGoogle ScholarPubMed
Arnoux, P. and Ito, S., Pisot substitutions and Rauzy fractals. Journées Montoises d’Informatique Théorique (Marne-la-Vallée, 2000), Bull. Belg. Math. Soc. Simon Stevin 8(2001), 181–207.CrossRefGoogle Scholar
Bartlett, A., Spectral theory of ℤd substitutions. Ergodic Theory Dynam. Systems 38(2018), 1289–1341. https://doi.org/10.1017/etds.2016.66CrossRefGoogle Scholar
Berthé, V., Complexité et automates cellulaires linéaires. Theor. Inform. Appl. 34(2000), 403–423. https://doi.org/10.1051/ita:2000124CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K., and Solomyak, B., Invariant measures on stationary Bratteli diagrams. Ergodic Theory Dynam. Systems 30(2010), 973–1007. https://doi.org/10.1017/S0143385709000443CrossRefGoogle Scholar
Bousquet-Mélou, M. and Petkov̌sek, M., Linear recurrences with constant coefficients: the multivariate case. Formal power series and algebraic combinatorics (Toronto, ON, 1998). Discrete Math. 225(2000), 51–75. https://doi.org/10.1016/S0012-365X(00)00147-3CrossRefGoogle Scholar
Boyle, M., Open problems in symbolic dynamics. In: Geometric and probabilistic structures in dynamics. Contemp. Math., 469, Amer. Math. Soc., Providence, RI, 2008, pp. 69–118. https://doi.org/10.1090/conm/469/09161CrossRefGoogle Scholar
Charlier, E., Rampersad, N., and Shallit, J., Enumeration and decidable properties of automatic sequences. Internat. J. Found. Comput. Sci. 23(2012), 1035–1066. https://doi.org/10.1142/S0129054112400448CrossRefGoogle Scholar
Christol, G., Ensembles presque periodiques k-reconnaissables. Theoret. Comput. Sci. 9(1979), 141–145. https://doi.org/10.1016/0304-3975(79)90011-2CrossRefGoogle Scholar
Christol, G., Kamae, T., Mendès France, M., and Rauzy, G., Suites algébriques, automates et substitutions. Bull. Soc. Math. France 108(1980), 401–419.CrossRefGoogle Scholar
Cobham, A., Uniform tag sequences. Math. Systems Theory 6(1972), 164–192. https://doi.org/10.1007/BF01706087CrossRefGoogle Scholar
Cyr, V. and Kra, B., Nonexpansive ℤ2-subdynamics and Nivat’s conjecture. Trans. Amer. Math. Soc. 367(2015), 6487–6537. https://doi.org/10.1090/S0002-9947-2015-06391-0CrossRefGoogle Scholar
Cyr, V. and Kra, B., Free ergodic ℤ2-systems and complexity. Proc. Amer. Math. Soc. 145(2017), 1163–1173. https://doi.org/10.1090/proc/13279CrossRefGoogle Scholar
Einsiedler, M., Invariant subsets and invariant measures for irreducible actions on zero-dimensional groups. Bull. London Math. Soc. 36(2004), 321–331. https://doi.org/10.1112/S0024609303003023CrossRefGoogle Scholar
Furstenberg, H., Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1(1967), 1–49. https://doi.org/10.1007/BF01692494CrossRefGoogle Scholar
Host, B., Maass, A., and Martínez, S., Uniform Bernoulli measure in dynamics of permutative cellular automata with algebraic local rules. Discrete Contin. Dyn. Syst. 9(2003), 1423–1446. https://doi.org/10.3934/dcds.2003.9.1423CrossRefGoogle Scholar
Kari, J. and Moutot, E., Nivat’s conjecture and pattern complexity in algebraic subshifts. Theoret. Comput. Sci. 777(2019), 379–386. https://doi.org/10.1016/j.tcs.2018.12.029CrossRefGoogle Scholar
Kitchens, B. and Schmidt, K., Markov subgroups of (Z/2Z)Z2. In: Symbolic dynamics and its applications (New Haven, CT, 1991), Contemp. Math., 135, Amer. Math. Soc., Providence, RI, 1992, pp. 265–283. https://doi.org/10.1090/conm/135/1185094CrossRefGoogle Scholar
Massuir, A., Peltomäki, J., and Rigo, M., Automatic sequences based on Parry or Bertrand numeration systems. Adv. in Appl. Math. 108(2019), 11–30. https://doi.org/10.1016/j.aam.2019.03.003CrossRefGoogle Scholar
Mossé, B., Puissances de mots et reconnaissabilité des points fixes d’une substitution. Theoret. Comput. Sci. 99(1992), 327–334. https://doi.org/10.1016/0304-3975(92)90357-LCrossRefGoogle Scholar
Mousavi, H., Automatic theorem proving in Walnut. https://cs.uwaterloo.ca/∼shallit/Papers/aut3.pdfGoogle Scholar
Pivato, M., Ergodic theory of cellular automata. In: Computational complexity. Vols. 1–6. Springer, New York, 2012, pp. 965–999. https://doi.org/10.1007/978-1-4614-1800-9_62CrossRefGoogle Scholar
Pivato, M. and Yassawi, R., Limit measures for affine cellular automata. Ergodic Theory Dynam. Systems 22(2002), 1269–1287. https://doi.org/10.1017/S0143385702000548CrossRefGoogle Scholar
Pivato, M. and Yassawi, R., The spatial structure of odometers in cellular automata. JAC 2008 (2009), 119–129.Google Scholar
Quas, A. and Zamboni, L., Periodicity and local complexity. Theoret. Comput. Sci. 319(2004), 229–240. https://doi.org/10.1016/j.tcs.2004.02.026CrossRefGoogle Scholar
Rigo, M., Formal languages, automata and numeration systems. 2. Applications to recognizability and decidability. Networks and Telecommunications Series. ISTE, London, John Wiley & Sons, Inc., Hoboken, NJ, 2014.Google Scholar
Rowland, E., IntegerSequences. https://github.com/ericrowland/IntegerSequencesGoogle Scholar
Rowland, E. and Yassawi, R., A characterization of p-automatic sequences as columns of linear cellular automata. Adv. in Appl. Math. 63(2015), 68–89. https://doi.org/10.1016/j.aam.2014.10.002CrossRefGoogle Scholar
Salon, O., Suites automatiques à multi-indices et algébricité. C. R. Acad. Sci. Paris Sér. I Math. 305(1987), 501–504.Google Scholar
Schmidt, K., Dynamical systems of algebraic origin. Progress in Mathematics, 128, Birkha̋user Verlag, Basel, 1995.Google Scholar
Silberger, S., Subshifts of the three dot system. Ergodic Theory Dynam. Systems 25(2005), 1673–1687. https://doi.org/10.1017/S0143385705000015CrossRefGoogle Scholar
Walters, P., An introduction to ergodic theory. Graduate Texts in Mathematics, 79, Springer-Verlag, New York, Berlin, 1982.CrossRefGoogle Scholar