Published online by Cambridge University Press: 28 October 2020
Let A be a two-dimensional abelian variety defined over a number field K. Fix a prime number 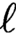 $\ell $
and suppose
$\ell $
and suppose
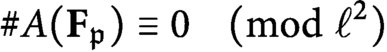 $\#A({\mathbf {F}_{\mathfrak {p}}}) \equiv 0 \pmod {\ell ^2}$
for a set of primes
$\#A({\mathbf {F}_{\mathfrak {p}}}) \equiv 0 \pmod {\ell ^2}$
for a set of primes
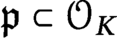 ${\mathfrak {p}} \subset {\mathcal {O}_{K}}$
of density 1. When
${\mathfrak {p}} \subset {\mathcal {O}_{K}}$
of density 1. When
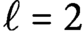 $\ell =2$
Serre has shown that there does not necessarily exist a K-isogenous
$\ell =2$
Serre has shown that there does not necessarily exist a K-isogenous
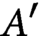 $A'$
such that
$A'$
such that
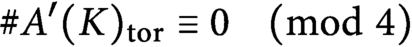 $\#A'(K)_{{tor}} \equiv 0 \pmod {4}$
. We extend those results to all odd
$\#A'(K)_{{tor}} \equiv 0 \pmod {4}$
. We extend those results to all odd
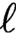 $\ell $
and classify the abelian varieties that fail this divisibility principle for torsion in terms of the image of the mod-
$\ell $
and classify the abelian varieties that fail this divisibility principle for torsion in terms of the image of the mod-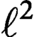 $\ell ^2$
representation.
$\ell ^2$
representation.