No CrossRef data available.
Published online by Cambridge University Press: 21 June 2019
The Peter–Weyl idempotent 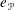 $e_{\mathscr{P}}$ of a parahoric subgroup
$e_{\mathscr{P}}$ of a parahoric subgroup 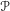 $\mathscr{P}$ is the sum of the idempotents of irreducible representations of
$\mathscr{P}$ is the sum of the idempotents of irreducible representations of 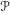 $\mathscr{P}$ that have a nonzero Iwahori fixed vector. The convolution algebra associated with
$\mathscr{P}$ that have a nonzero Iwahori fixed vector. The convolution algebra associated with 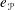 $e_{\mathscr{P}}$ is called a Peter–Weyl Iwahori algebra. We show that any Peter–Weyl Iwahori algebra is Morita equivalent to the Iwahori–Hecke algebra. Both the Iwahori–Hecke algebra and a Peter–Weyl Iwahori algebra have a natural conjugate linear anti-involution
$e_{\mathscr{P}}$ is called a Peter–Weyl Iwahori algebra. We show that any Peter–Weyl Iwahori algebra is Morita equivalent to the Iwahori–Hecke algebra. Both the Iwahori–Hecke algebra and a Peter–Weyl Iwahori algebra have a natural conjugate linear anti-involution  $\star$, and the Morita equivalence preserves irreducible hermitian and unitary modules. Both algebras have another anti-involution, denoted by
$\star$, and the Morita equivalence preserves irreducible hermitian and unitary modules. Both algebras have another anti-involution, denoted by  $\bullet$, and the Morita equivalence preserves irreducible and unitary modules for
$\bullet$, and the Morita equivalence preserves irreducible and unitary modules for  $\bullet$.
$\bullet$.
Author D.B. is partly supported by NSA grant H98230-16-1-0006. Author A.M. is partly supported by Hong Kong Research Grants Council grant CERG #16301915.