Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T10:17:58.336Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple Formulas for Constellations and Bipartite Maps with Prescribed Degrees

Part of: Quantum field theory; related classical field theories Geometric probability and stochastic geometry

Published online by Cambridge University Press:  12 November 2019

Baptiste Louf
Baptiste Louf*
Affiliation:
IRIF, Université Paris Diderot - Paris 7, Bâtiment Sophie Germain, 75205Paris Cedex 13, France Email: blouf@irif.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain simple quadratic recurrence formulas counting bipartite maps on surfaces with prescribed degrees (in particular, 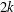$2k$-angulations) and constellations. These formulas are the fastest known way of computing these numbers.

Our work is a natural extension of previous works on integrable hierarchies (2-Toda and KP), namely, the Pandharipande recursion for Hurwitz numbers (proved by Okounkov and simplified by Dubrovin–Yang–Zagier), as well as formulas for several models of maps (Goulden–Jackson, Carrell–Chapuy, Kazarian–Zograf). As for those formulas, a bijective interpretation is still to be found. We also include a formula for monotone simple Hurwitz numbers derived in the same fashion.

These formulas also play a key role in subsequent work of the author with T. Budzinski establishing the hyperbolic local limit of random bipartite maps of large genus.

Keywords

mapHurwitz numberToda hierarchyconstellation

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 81T40: Two-dimensional field theories, conformal field theories, etc. 81T20: Quantum field theory on curved space backgrounds
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 1 , February 2021 , pp. 160 - 176
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

BL is supported by ERC-2016-STG 716083 “CombiTop”.

References

Adrianov, N. M., An analogue of the Harer–Zagier formula for unicellular two-color maps. Funktsional. Anal. i Prilozhen. 31(1997), 1–9, 95. https://doi.org/10.1007/BF02465782CrossRefGoogle Scholar
Albenque, M. and Poulalhon, D., Generic method for bijections between blossoming trees and planar maps. Electron. J. Combin. 22(2015), paper P2.38. https://doi.org/10.37236/3386CrossRefGoogle Scholar
Alexandrov, A., Chapuy, G., Eynard, B., and Harnad, J., Fermionic approach to weighted Hurwitz numbers and topological recursion. Comm. Math. Phys. 360(2018), 777–826. https://doi.org/10.1007/s00220-017-3065-9CrossRefGoogle Scholar
Bender, E. A. and Canfield, E. R., The asymptotic number of rooted maps on a surface. J. Combin. Theory Ser. A 43(1986), 244–257.CrossRefGoogle Scholar
Bernardi, O. and Fusy, E., A bijection for triangulations, quadrangulations, pentagulations, etc. J. Combin. Theory Ser. A 119(2012), 218–244. https://doi.org/10.1016/j.jcta.2011.08.006CrossRefGoogle Scholar
Bouttier, J., Di Francesco, P., and Guitter, E., Planar maps as labeled mobiles. Electron. J. Combin. 11(2004), R69.CrossRefGoogle Scholar
Budzinski, T. and Louf, B., Local limits of uniform triangulations in high genus. 2019. arxiv:abs/1902.00492.CrossRefGoogle Scholar
Carrell, S. R. and Chapuy, G., Simple recurrence formulas to count maps on orientable surfaces. J. Combin. Theory Ser. A 133(2015), 58–75. https://doi.org/10.1016/j.jcta.2015.01.005CrossRefGoogle Scholar
Chapuy, G., Asymptotic enumeration of constellations and related families of maps on orientable surfaces. Combin. Probab. Comput. 18(2009), 477–516. https://doi.org/10.1017/S0963548309009808CrossRefGoogle Scholar
Chapuy, G., A new combinatorial identity for unicellular maps, via a direct bijective approach. Adv. in Appl. Math. 47(2011), 874–893. https://doi.org/10.1016/j.aam.2011.04.004CrossRefGoogle Scholar
Chapuy, G. and Fang, W., Generating functions of bipartite maps on orientable surfaces. Electron. J. Combin. 23(2016), Paper 3.31. https://doi.org/10.37236/5511CrossRefGoogle Scholar
Chapuy, G., Féray, V., and Fusy, E., A simple model of trees for unicellular maps. J. Combin. Theory Ser. A 120(2013), 2064–2092. https://doi.org/10.1016/j.jcta.2013.08.003CrossRefGoogle Scholar
Chapuy, G., Marcus, M., and Schaeffer, G., A bijection for rooted maps on orientable surfaces. SIAM J. Discrete Math. 23(2009), 1587–1611. https://doi.org/10.1137/080720097CrossRefGoogle Scholar
Curien, N., Planar stochastic hyperbolic triangulations. Probab. Theory Related Fields 165(2016), 509–540. https://doi.org/10.1007/s00440-015-0638-4CrossRefGoogle Scholar
Dubrovin, B., Yang, Di, and Zagier, D, Classical Hurwitz numbers and related combinatorics. Mosc. Math. J. 17(2017), 601–633. https://doi.org/10.17323/1609-4514-2016-16-4-601-633CrossRefGoogle Scholar
Eynard, B., Counting surfaces. In: CRM Aisenstadt chair lectures. Progress in Mathematical Physics, 70, Birkhäuser/Springer, Cham, 2016. https://doi.org/10.1007/978-3-7643-8797-6Google Scholar
Gao, Z., The number of degree restricted maps on general surfaces. Discrete Math. 123(1993), 47–63. https://doi.org/10.1016/0012-365X(93)90006-FCrossRefGoogle Scholar
Goulden, I. P., Guay-Paquet, M., and Novak, J., Monotone Hurwitz numbers and the HCIZ integral. Ann. Math. Blaise Pascal 21(2014), 71–89.CrossRefGoogle Scholar
Goulden, I. P. and Jackson, D. M., The KP hierarchy, branched covers, and triangulations. Adv. Math. 219(2008), 932–951. https://doi.org/10.1016/j.aim.2008.06.013CrossRefGoogle Scholar
Guay-Paquet, M. and Harnad, J., 2D Toda -functions as combinatorial generating functions. Lett. Math. Phys. 105(2015), 827–852. https://doi.org/10.1007/s11005-015-0756-zCrossRefGoogle Scholar
Kazarian, M. and Zograf, P., Virasoro constraints and topological recursion for Grothendieck’s dessin counting. Lett. Math. Phys. 105(2015), 1057–1084. https://doi.org/10.1007/s11005-015-0771-0CrossRefGoogle Scholar
Lepoutre, M., Blossoming bijection for higher-genus maps. J. Combin. Theory Ser. A 165(2019), 187–224. https://doi.org/10.1016/j.jcta.2019.01.005CrossRefGoogle Scholar
Louf, B., A new family of bijections for planar maps. J. Combin. Theory Ser. A 168(2019), 374–395. https://doi.org/10.1016/j.jcta.2019.06.006CrossRefGoogle Scholar
Miwa, T., Jimbo, M., and Date, E., Solitons. Differential equations, symmetries, and infinite dimensional algebras. Cambridge Tracts in Mathematics, 135, Cambridge University Press, Cambridge, 2000.Google Scholar
Okounkov, A., Toda equations for Hurwitz numbers. Math. Res. Lett. 7(2000), 447–453. https://doi.org/10.4310/MRL.2000.v7.n4.a10CrossRefGoogle Scholar
Okounkov, A., Infinite wedge and random partitions. Selecta Math. (N. S.) 7(2001), 57–81. https://doi.org/10.1007/PL00001398CrossRefGoogle Scholar
Pandharipande, R., The Toda equations and the Gromov–Witten theory of the Riemann sphere. Lett. Math. Phys. 53(2000), 59–74. https://doi.org/10.1023/A:1026571018707CrossRefGoogle Scholar
Poulalhon, D. and Schaeffer, G., Factorizations of large cycles in the symmetric group. Discrete Math. 254(2002), 433–458. https://doi.org/10.1016/S0012-365X(01)00361-2CrossRefGoogle Scholar
Schaeffer, G., Conjugaison d’arbres et cartes combinatoires aléatoires. Thèse de doctorat, Université Bordeaux I, 1998.Google Scholar
Tutte, W. T., A census of planar maps. Canad. J. Math. 15(1963), 249–271. https://doi.org/10.4153/CJM-1963-029-xCrossRefGoogle Scholar
Walsh, T. R. S. and Lehman, A. B., Counting rooted maps by genus. I. J. Combin. Theory Ser. B 13(1972), 192–218. https://doi.org/10.1016/0095-8956(72)90056-1CrossRefGoogle Scholar