Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:00:46.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Annihilators of the Ideal Class Group of a Cyclic Extension of an Imaginary Quadratic Field

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  09 January 2019

Hugo Chapdelaine  and
Radan Kučera
Hugo Chapdelaine
Affiliation:
Faculty of Science and Engineering, Laval University, Québec G1V 0A6, Canada Email: hugo.chapdelaine@mat.ulaval.ca
Radan Kučera
Affiliation:
Faculty of Science, Masaryk University, 611 37 Brno, Czech Republic Email: kucera@math.muni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to study the group of elliptic units of a cyclic extension 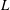$L$ of an imaginary quadratic field 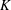$K$ such that the degree 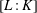$[L:K]$ is a power of an odd prime 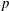$p$. We construct an explicit root of the usual top generator of this group, and we use it to obtain an annihilation result of the 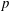$p$-Sylow subgroup of the ideal class group of 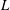$L$.

Keywords

annihilatorclass groupelliptic unit

MSC classification

Primary: 11R20: Other abelian and metabelian extensions
Secondary: 11R27: Units and factorization 11R29: Class numbers, class groups, discriminants
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1395 - 1419
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The second author was supported under Project 15-15785S of the Czech Science Foundation.

References

Bley, W., Wild Euler systems of elliptic units and the equivariant Tamagawa number conjecture . J. Reine Angew. Math. 577(2004), 117–146. https://doi.org/10.1515/crll.2004.2004.577.117.Google Scholar
Bley, W., Equivariant Tamagawa number conjecture for abelian extensions of a quadratic imaginary field . Doc. Math. 11(2006), 73–118.Google Scholar
Burns, D., Congruences between derivatives of abelian L-functions at s = 0 . Invent. Math. 169(2007), 451–499. https://doi.org/10.1007/s00222-007-0052-3.Google Scholar
Gras, G., Class field theory. From theory to practice . Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree . Acta Arith. 112(2004), 177–198. https://doi.org/10.4064/aa112-2-6.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree II . Canad. J. Math. 58(2006), 580–599. https://doi.org/10.4153/CJM-2006-024-2.Google Scholar
Greither, C. and Kučera, R., Linear forms on Sinnott’s module . J. Number Theory 141(2014), 324–342. https://doi.org/10.1016/j.jnt.2014.02.003.Google Scholar
Greither, C. and Kučera, R., Eigenspaces of the ideal class group . Ann. Inst. Fourier (Grenoble) 64(2014), 2165–2203. https://doi.org/10.5802/aif.2908.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree III . Publ. Math. Debrecen 86(2015), no. 3–4, 401–421.Google Scholar
Ohshita, T., On higher Fitting ideals of Iwasawa modules of ideal class groups over imaginary quadratic fields and Euler systems of elliptic units . Kyoto J. Math. 53(2013), 845–887. https://doi.org/10.1215/21562261-2366118.Google Scholar
Oukhaba, H., Index formulas for ramified elliptic units . Compositio Math. 137(2003), 1–22. https://doi.org/10.1023/A:1023667807218.Google Scholar
Rubin, K., Global units and ideal class groups . Invent. Math. 89(1987), 511–526. https://doi.org/10.1007/BF01388983.Google Scholar
Rubin, K., Stark units and Kolyvagin’s “Euler systems” . J. Reine Angew. Math. 425(1992), 141–154. https://doi.org/10.1515/crll.1992.425.141.Google Scholar
Sinnott, W., On the Stickelberger ideal and the circular units of an abelian field . Invent. Math. 62(1980), 181–234. https://doi.org/10.1007/BF01389158.Google Scholar
Thaine, F., On the ideal class groups of real abelian number fields . Ann. of Math. (2) 128(1988), no. 1, 1–18. https://doi.org/10.2307/1971460.Google Scholar