No CrossRef data available.
Published online by Cambridge University Press: 09 January 2025
Let 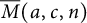 $\overline {M}(a,c,n)$ denote the number of overpartitions of n with first residual crank congruent to a modulo c with
$\overline {M}(a,c,n)$ denote the number of overpartitions of n with first residual crank congruent to a modulo c with  $c\geq 3$ being odd and
$c\geq 3$ being odd and  $0\leq a<c$. The central objective of this paper is twofold: firstly, to establish an asymptotic formula for the crank of overpartitions; and secondly, to establish several inequalities concerning
$0\leq a<c$. The central objective of this paper is twofold: firstly, to establish an asymptotic formula for the crank of overpartitions; and secondly, to establish several inequalities concerning  $\overline {M}(a,c,n)$ that encompasses crank differences, positivity, and strict log-subadditivity.
$\overline {M}(a,c,n)$ that encompasses crank differences, positivity, and strict log-subadditivity.
The first author is supported by the National Natural Science Foundation of China (Grant No. 12401432) and the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202200614). The second author is supported by the National Natural Science Foundation of China (Grant No. 12371327) and the Natural Science Foundation of Chongqing (Grant No. cstc2021jcyj-msxmX0107).