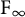1 Introduction
In this paper, we introduce and study braided versions of self-similar groups of tree automorphisms and Röver–Nekrashevych groups of tree almost-automorphisms. A subgroup of the group of automorphisms of an infinite rooted regular tree is called “self-similar” if it is “built out of copies of itself” in some sense (see Definition 2.2). The Röver–Nekrashevych group associated with a self-similar group is the group of self-homeomorphisms of the boundary of the tree that locally “look like” the self-similar group (see Definition 3.4). The first example, now called the “Röver group,” was constructed by Röver in [Reference RöverRöv99], using the Grigorchuk group constructed by Grigorchuk in [Reference GrigorchukGri80, Reference GrigorchukGri84]. In [Reference NekrashevychNek04], Nekrashevych constructed Röver–Nekrashevych groups in general, starting with an arbitrary self-similar group.
The braided variants of Röver–Nekrashevych groups we construct here were previously considered by Aroca and Cumplido [Reference AllcockAC22] in the special case when the self-similar groups are what we call “self-identical” (Definition 2.3), and these examples were also studied by the first author and Wu in [Reference Skipper and ZaremskySW]. These papers are part of a large body of recent work devoted to “braiding” groups in the extended family of Thompson’s groups. The original braided Thompson group
![]() $\operatorname {br}\!V$
was introduced independently by Brin [Reference BrinBri07] and Dehornoy [Reference DegenhardtDeh06], as a braided version of the classical Thompson group V. Thompson’s group F also has a braided counterpart
$\operatorname {br}\!V$
was introduced independently by Brin [Reference BrinBri07] and Dehornoy [Reference DegenhardtDeh06], as a braided version of the classical Thompson group V. Thompson’s group F also has a braided counterpart
![]() $\operatorname {br}\!F$
, first considered in [Reference Belk and MatucciBBCS08]. Thompson’s group T has a number of different “braidings,” found, e.g., in [Reference Fluch, Marschler, Witzel and ZaremskyFK08, Reference Funar and KapoudjianFK11, Reference WitzelWit19]. Braided versions of the Brin–Thompson groups from [Reference BrinBri04] were recently constructed by Spahn [Reference Skipper, Witzel and ZaremskySpa]. Finally, Houghton’s groups, which are related to Thompson’s groups, have braided variants due to Degenhardt [Reference de la HarpeDeg00]. The braided Houghton groups along with the braided versions of T from [Reference Fluch, Marschler, Witzel and ZaremskyFK08, Reference Funar and KapoudjianFK11] are also studied in [Reference GeogheganGLU22].
$\operatorname {br}\!F$
, first considered in [Reference Belk and MatucciBBCS08]. Thompson’s group T has a number of different “braidings,” found, e.g., in [Reference Fluch, Marschler, Witzel and ZaremskyFK08, Reference Funar and KapoudjianFK11, Reference WitzelWit19]. Braided versions of the Brin–Thompson groups from [Reference BrinBri04] were recently constructed by Spahn [Reference Skipper, Witzel and ZaremskySpa]. Finally, Houghton’s groups, which are related to Thompson’s groups, have braided variants due to Degenhardt [Reference de la HarpeDeg00]. The braided Houghton groups along with the braided versions of T from [Reference Fluch, Marschler, Witzel and ZaremskyFK08, Reference Funar and KapoudjianFK11] are also studied in [Reference GeogheganGLU22].
In this paper, we “braid” arbitrary self-similar groups and arbitrary Röver–Nekrashevych groups. In particular, we get a new group that we call the braided Röver group, which is a braided variant of the Röver group, i.e., the Röver–Nekrashevych group specifically arising from the Grigorchuk group. (A torsion-free version of the Grigorchuk group that could be called a “braided” version was previously constructed by Grigorchuk in [Reference GrigorchukGri85]; the braided Grigorchuk group we construct here is slightly different.) To construct braided self-similar groups, we work inside an infinitely iterated wreath product of braid groups, and impose conditions arising from a “braided wreath recursion” on elements (see Definition 2.5). To construct braided Röver–Nekrashevych groups, we use the framework of d-ary cloning systems, developed by the authors and Witzel in [Reference SteinSZ21, Reference Witzel and ZaremskyWZ18]: we use the braided wreath recursion to produce a d-ary cloning system associated with any braided self-similar group, and then the braided Röver–Nekrashevych group is the resulting Thompson-like group that arises from the d-ary cloning system (see Definition 3.6).
As often happens with new Thompson-like groups, for example, in many of the aforementioned references, it is of interest to understand their finiteness properties. A group is of type
![]() $F_n$
if it has a classifying space with finite n-skeleton, where a classifying space is a connected CW-complex whose fundamental group is the group in question and whose higher homotopy groups are all trivial. Thus, type
$F_n$
if it has a classifying space with finite n-skeleton, where a classifying space is a connected CW-complex whose fundamental group is the group in question and whose higher homotopy groups are all trivial. Thus, type
![]() $\operatorname {\mathrm {F}}_1$
is equivalent to finite generation and type
$\operatorname {\mathrm {F}}_1$
is equivalent to finite generation and type
![]() $\operatorname {\mathrm {F}}_2$
is equivalent to finite presentability. We say type
$\operatorname {\mathrm {F}}_2$
is equivalent to finite presentability. We say type
![]() $F_\infty $
for type
$F_\infty $
for type
![]() $\operatorname {\mathrm {F}}_n$
for all n. The classical Thompson’s groups F, T, and V, and the Brin–Thompson groups
$\operatorname {\mathrm {F}}_n$
for all n. The classical Thompson’s groups F, T, and V, and the Brin–Thompson groups
![]() $nV$
, are all of type
$nV$
, are all of type
![]() $\operatorname {\mathrm {F}}_\infty $
[Reference Berns-Zieve, Fry, Gillings, Hoganson and MathewsBG84, Reference BrothierBro87, Reference Funar and KapoudjianFMWZ13], as are all their aforementioned braided variants [Reference Benli, Grigorchuk and de la HarpeBFM+16, Reference GeogheganGLU22, Reference Skipper, Witzel and ZaremskySpa, Reference WitzelWit19. There is also a “ribbon braided” variant of V that is of type
$\operatorname {\mathrm {F}}_\infty $
[Reference Berns-Zieve, Fry, Gillings, Hoganson and MathewsBG84, Reference BrothierBro87, Reference Funar and KapoudjianFMWZ13], as are all their aforementioned braided variants [Reference Benli, Grigorchuk and de la HarpeBFM+16, Reference GeogheganGLU22, Reference Skipper, Witzel and ZaremskySpa, Reference WitzelWit19. There is also a “ribbon braided” variant of V that is of type
![]() $\operatorname {\mathrm {F}}_\infty $
[Reference ThumannThu17]. The Röver group along with some related Röver–Nekrashevych groups are of type
$\operatorname {\mathrm {F}}_\infty $
[Reference ThumannThu17]. The Röver group along with some related Röver–Nekrashevych groups are of type
![]() $\operatorname {\mathrm {F}}_\infty $
as well [Reference Brady, Burillo, Cleary and SteinBM16, Reference Farley and HughesFH15, Reference SteinSZ21]. In particular, this includes Röver–Nekrashevych groups arising from self-identical groups [Reference Farley and HughesFH15]. Röver–Nekrashevych groups also afforded the first known examples of simple groups of type
$\operatorname {\mathrm {F}}_\infty $
as well [Reference Brady, Burillo, Cleary and SteinBM16, Reference Farley and HughesFH15, Reference SteinSZ21]. In particular, this includes Röver–Nekrashevych groups arising from self-identical groups [Reference Farley and HughesFH15]. Röver–Nekrashevych groups also afforded the first known examples of simple groups of type
![]() $\operatorname {\mathrm {F}}_{n-1}$
but not
$\operatorname {\mathrm {F}}_{n-1}$
but not
![]() $\operatorname {\mathrm {F}}_n$
for arbitrary n, in [Reference SpahnSWZ19]. Here, we analyze finiteness properties of braided Röver–Nekrashevych groups, and prove two main results.
$\operatorname {\mathrm {F}}_n$
for arbitrary n, in [Reference SpahnSWZ19]. Here, we analyze finiteness properties of braided Röver–Nekrashevych groups, and prove two main results.
Theorem 4.1 Let
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
be braided self-similar. If G is of type
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
be braided self-similar. If G is of type
![]() $\operatorname {\mathrm {F}}_n$
then so is
$\operatorname {\mathrm {F}}_n$
then so is
![]() $\operatorname {br}\!V_d(G)$
.
$\operatorname {br}\!V_d(G)$
.
Theorem 5.1 The braided Röver group is of type
![]() $\operatorname {\mathrm {F}}_\infty $
.
$\operatorname {\mathrm {F}}_\infty $
.
When G is braided self-identical, Theorem 4.1 was proved by the first author and Wu in [Reference Skipper and ZaremskySW], where it was proved that the converse also holds. We prove that the braided Grigorchuk group is (like the original Grigorchuk group) not finitely presentable (Proposition 2.14), so Theorem 5.1 shows that the converse of Theorem 4.1 is not true in general. We remark that it remains an interesting problem for
![]() $n\ge 2$
to find explicit examples of G for which Theorem 4.1 applies but the results in [Reference Skipper and ZaremskySW] do not, i.e., G is braided self-similar but not braided self-identical. (For example, when
$n\ge 2$
to find explicit examples of G for which Theorem 4.1 applies but the results in [Reference Skipper and ZaremskySW] do not, i.e., G is braided self-similar but not braided self-identical. (For example, when
![]() $n=1$
, see Example 2.5 using
$n=1$
, see Example 2.5 using
![]() $\mathbb {Z}\wr \mathbb {Z}$
.) In another direction, for G a braided self-similar group and
$\mathbb {Z}\wr \mathbb {Z}$
.) In another direction, for G a braided self-similar group and
![]() $\pi (G)$
its corresponding (non-braided) self-similar group, it would be interesting to try and relate the finiteness properties of G to those of
$\pi (G)$
its corresponding (non-braided) self-similar group, it would be interesting to try and relate the finiteness properties of G to those of
![]() $\pi (G)$
, and the finiteness properties of
$\pi (G)$
, and the finiteness properties of
![]() $\operatorname {br}\!V_d(G)$
to those of
$\operatorname {br}\!V_d(G)$
to those of
![]() $V_d(\pi (G))$
; we leave this for future investigation.
$V_d(\pi (G))$
; we leave this for future investigation.
This paper also rectifies a gap in the literature, namely we construct the so-called Stein–Farley complex for a general d-ary cloning system. When
![]() $d=2$
, this was done by Witzel and the second author in the original cloning systems paper [Reference Witzel and ZaremskyWZ18], but for general d-ary cloning systems, introduced in [Reference SteinSZ21], the Stein–Farley complex was only constructed for a special case involving self-similar groups. Here, we officially construct the Stein–Farley complex for an arbitrary d-ary cloning system (Section 4.1). The construction is straightforward, and works essentially by combining the ideas from the two aforementioned special cases, but had not technically been done before. These complexes are a key tool in proving Theorem 4.1.
$d=2$
, this was done by Witzel and the second author in the original cloning systems paper [Reference Witzel and ZaremskyWZ18], but for general d-ary cloning systems, introduced in [Reference SteinSZ21], the Stein–Farley complex was only constructed for a special case involving self-similar groups. Here, we officially construct the Stein–Farley complex for an arbitrary d-ary cloning system (Section 4.1). The construction is straightforward, and works essentially by combining the ideas from the two aforementioned special cases, but had not technically been done before. These complexes are a key tool in proving Theorem 4.1.
In order to prove Theorem 5.1, we introduce a new type of complex defined on a surface, which we call the “
![]() $(2,5/2)$
-disk complex” (see Definition 5.8). A vertex of this complex is an isotopy class of an embedded disk, enclosing two marked points in its interior and either
$(2,5/2)$
-disk complex” (see Definition 5.8). A vertex of this complex is an isotopy class of an embedded disk, enclosing two marked points in its interior and either
![]() $0$
or
$0$
or
![]() $1$
marked points in its boundary, and a collection of vertices span a simplex whenever the disks are pairwise disjoint or nested. The higher connectivity properties of the descending links in the Stein–Farley complex for the braided Röver group turn out to be informed by those of the
$1$
marked points in its boundary, and a collection of vertices span a simplex whenever the disks are pairwise disjoint or nested. The higher connectivity properties of the descending links in the Stein–Farley complex for the braided Röver group turn out to be informed by those of the
![]() $(2,5/2)$
-disk complex, and this complex seems to be of interest in its own right, given its connection to (braided versions of) the Grigorchuk and Röver groups.
$(2,5/2)$
-disk complex, and this complex seems to be of interest in its own right, given its connection to (braided versions of) the Grigorchuk and Röver groups.
This paper is organized as follows: In Section 2, we recall the background on self-similar groups, and define braided self-similar groups. In Section 3, we recall the background on d-ary cloning systems and Röver–Nekrashevych groups, and define braided Röver–Nekrashevych groups, including the braided Röver group. In Section 4, we construct Stein–Farley complexes for arbitrary d-ary cloning systems (which has technically not been done before), and then focus on the case of braided Röver–Nekrashevych groups to prove Theorem 4.1. Finally, in Section 5, we prove Theorem 5.1, that the braided Röver group is of type
![]() $\operatorname {\mathrm {F}}_\infty $
.
$\operatorname {\mathrm {F}}_\infty $
.
2 Braiding groups of automorphisms of trees
Let
![]() $d\in \mathbb {N}$
with
$d\in \mathbb {N}$
with
![]() $d\ge 2$
, let X be a set with d elements, called an alphabet, and let
$d\ge 2$
, let X be a set with d elements, called an alphabet, and let
![]() $X^*$
be the set of all finite words in X (including the empty word, denoted
$X^*$
be the set of all finite words in X (including the empty word, denoted
![]() $\varnothing $
). The infinite rooted d-ary tree, denoted
$\varnothing $
). The infinite rooted d-ary tree, denoted
![]() $\mathcal {T}_d$
, naturally has
$\mathcal {T}_d$
, naturally has
![]() $X^*$
as its vertex set. The root is
$X^*$
as its vertex set. The root is
![]() $\varnothing $
, and given a vertex v, the children of v are the vertices of the form
$\varnothing $
, and given a vertex v, the children of v are the vertices of the form
![]() $vx$
for
$vx$
for
![]() $x\in X$
.
$x\in X$
.
Definition 2.1 (Automorphism)
An automorphism of
![]() $\mathcal {T}_d$
is a bijection
$\mathcal {T}_d$
is a bijection
![]() $X^*\to X^*$
that preserves incidence (and so in particular fixes
$X^*\to X^*$
that preserves incidence (and so in particular fixes
![]() $\varnothing $
). The group of all automorphisms of
$\varnothing $
). The group of all automorphisms of
![]() $\mathcal {T}_d$
is denoted
$\mathcal {T}_d$
is denoted
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
.
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
.
We will be interested in certain subgroups of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, called self-similar groups. A vast amount of information about self-similar groups can be found in [Reference NekrashevychNek05]. To define them, we need to view
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, called self-similar groups. A vast amount of information about self-similar groups can be found in [Reference NekrashevychNek05]. To define them, we need to view
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
as an infinitely iterated wreath product, namely
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
as an infinitely iterated wreath product, namely
as we will now begin to explain.
Our convention for wreath products is that
![]() , i.e., the group doing the acting is written on the left. We write the subscript X in
, i.e., the group doing the acting is written on the left. We write the subscript X in
![]() $\wr _X$
to emphasize that this is the permutation wreath product coming from
$\wr _X$
to emphasize that this is the permutation wreath product coming from
![]() acting on X. We may also sometimes identify X with
acting on X. We may also sometimes identify X with
![]() $\{1,\dots ,d\}$
so that elements of
$\{1,\dots ,d\}$
so that elements of
![]() $G^X$
can be conveniently written as tuples
$G^X$
can be conveniently written as tuples
![]() $(g_1,\dots ,g_d)$
. We will also sometimes write
$(g_1,\dots ,g_d)$
. We will also sometimes write
![]() $S_d \wr _X^\infty S_d$
for
$S_d \wr _X^\infty S_d$
for
![]() $S_d \wr _X(S_d \wr _X(S_d \wr _X\cdots ))$
.
$S_d \wr _X(S_d \wr _X(S_d \wr _X\cdots ))$
.
Now let us be more rigorous about infinitely iterated wreath products. Let
![]() $S_d \wr _X^n S_d$
be the n-times-iterated wreath product, e.g.,
$S_d \wr _X^n S_d$
be the n-times-iterated wreath product, e.g.,
 $$ \begin{align*} S_d\wr_X^0 S_d &= S_d,\\ S_d \wr_X^1 S_d &= S_d \wr_X S_d,\\ S_d \wr_X^2 S_d &= S_d \wr_X (S_d \wr_X S_d) \text{,} \end{align*} $$
$$ \begin{align*} S_d\wr_X^0 S_d &= S_d,\\ S_d \wr_X^1 S_d &= S_d \wr_X S_d,\\ S_d \wr_X^2 S_d &= S_d \wr_X (S_d \wr_X S_d) \text{,} \end{align*} $$
and so forth. For each
![]() $n\in \mathbb {N}$
, we have an epimorphism
$n\in \mathbb {N}$
, we have an epimorphism
![]() $S_d \wr _X^n S_d \to S_d \wr _X^{n-1} S_d$
given by “forgetting the rightmost factor”; for example,
$S_d \wr _X^n S_d \to S_d \wr _X^{n-1} S_d$
given by “forgetting the rightmost factor”; for example,
![]() $S_d \wr _X^2 S_d \to S_d \wr _X^1 S_d$
is the map
$S_d \wr _X^2 S_d \to S_d \wr _X^1 S_d$
is the map
This forms a projective system, and the infinitely iterated wreath product
![]() $S_d \wr _X^\infty S_d$
is the projective limit of this system. It is clear that this is isomorphic to
$S_d \wr _X^\infty S_d$
is the projective limit of this system. It is clear that this is isomorphic to
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. The point is that an automorphism of
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. The point is that an automorphism of
![]() $\mathcal {T}_d$
can be viewed as first shuffling the d many children of the root, then independently for each child of the root shuffling its d many children, then shuffling their children, and so on.
$\mathcal {T}_d$
can be viewed as first shuffling the d many children of the root, then independently for each child of the root shuffling its d many children, then shuffling their children, and so on.
Thanks to this viewpoint, we see that
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\cong S_d\wr _X\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Hence, an element
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\cong S_d\wr _X\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Hence, an element
![]() $f\in \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
can be decomposed as
$f\in \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
can be decomposed as
![]() $f=\rho (f)(f_1,\dots ,f_d)$
, where
$f=\rho (f)(f_1,\dots ,f_d)$
, where
is the natural epimorphism coming from the wreath product, and
![]() $f_i\in \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. This is called the wreath recursion. This produces a function (not a homomorphism)
$f_i\in \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. This is called the wreath recursion. This produces a function (not a homomorphism)
![]() $\psi \colon \operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
sending f to
$\psi \colon \operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
sending f to
so the wreath recursion of f is
![]() $f=\rho (f)\psi (f)$
. For any subgroup
$f=\rho (f)\psi (f)$
. For any subgroup
![]() $G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the image
$G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the image
![]() $\psi (G)$
is a subset of
$\psi (G)$
is a subset of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
, and this leads us to the definition of self-similar.
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
, and this leads us to the definition of self-similar.
Definition 2.2 (Self-similar)
A subgroup
![]() $G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called self-similar if
$G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called self-similar if
![]() $\psi (G)\subseteq G^X$
.
$\psi (G)\subseteq G^X$
.
The easiest example of a self-similar subgroup of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is given by a certain action of the symmetric group
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is given by a certain action of the symmetric group
![]() $S_d$
on
$S_d$
on
![]() $\mathcal {T}_d$
. This kind of example will come up a lot, so we will actually give it its own name.
$\mathcal {T}_d$
. This kind of example will come up a lot, so we will actually give it its own name.
Definition 2.3 (Self-identical)
A subgroup
![]() $G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called self-identical if
$G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called self-identical if
for all
![]() $g\in G$
.
$g\in G$
.
Example 2.1 (Subgroups of the symmetric group)
For
![]() $\sigma \in S_d=\operatorname {\mathrm {Symm}}(X)$
, we can define an element of
$\sigma \in S_d=\operatorname {\mathrm {Symm}}(X)$
, we can define an element of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, also denoted
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, also denoted
![]() $\sigma $
, by declaring that
$\sigma $
, by declaring that
![]() $\sigma $
sends the vertex
$\sigma $
sends the vertex
![]() $v=x_1\cdots x_k$
to the vertex
$v=x_1\cdots x_k$
to the vertex
![]() . Note that the wreath recursion of
. Note that the wreath recursion of
![]() $\sigma $
is
$\sigma $
is
![]() $\sigma =\sigma (\sigma ,\dots ,\sigma )$
. In particular,
$\sigma =\sigma (\sigma ,\dots ,\sigma )$
. In particular,
![]() $\psi (\sigma )=(\sigma ,\dots ,\sigma )$
, and so viewing
$\psi (\sigma )=(\sigma ,\dots ,\sigma )$
, and so viewing
![]() $S_d$
as a subgroup of
$S_d$
as a subgroup of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
in this way we see that
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
in this way we see that
![]() $S_d$
, and indeed any subgroup of
$S_d$
, and indeed any subgroup of
![]() $S_d$
, is self-identical (hence self-similar). Every self-identical subgroup occurs in this way.
$S_d$
, is self-identical (hence self-similar). Every self-identical subgroup occurs in this way.
Example 2.2 (Grigorchuk group)
The Grigorchuk group, introduced by Grigorchuk in [Reference GrigorchukGri80], is the subgroup
![]() $\operatorname {\mathrm {Grig}}\le \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
generated by elements
$\operatorname {\mathrm {Grig}}\le \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
generated by elements
![]() $\overline {a}$
,
$\overline {a}$
,
![]() $\overline {b}$
,
$\overline {b}$
,
![]() $\overline {c}$
, and
$\overline {c}$
, and
![]() $\overline {d}$
defined by the following wreath recursions. (These are usually denoted by a, b, c, and d, but we will be writing those for the braided version, so we will write
$\overline {d}$
defined by the following wreath recursions. (These are usually denoted by a, b, c, and d, but we will be writing those for the braided version, so we will write
![]() $\overline {a}$
,
$\overline {a}$
,
![]() $\overline {b}$
,
$\overline {b}$
,
![]() $\overline {c}$
, and
$\overline {c}$
, and
![]() $\overline {d}$
here.) First,
$\overline {d}$
here.) First,
![]() $\overline {a}=(1~2)(\operatorname {\mathrm {id}},\operatorname {\mathrm {id}})$
, where we identify X with
$\overline {a}=(1~2)(\operatorname {\mathrm {id}},\operatorname {\mathrm {id}})$
, where we identify X with
![]() $\{1,2\}$
. Next,
$\{1,2\}$
. Next,
![]() $\overline {b}=(\overline {a},\overline {c})$
,
$\overline {b}=(\overline {a},\overline {c})$
,
![]() $\overline {c}=(\overline {a},\overline {d})$
, and
$\overline {c}=(\overline {a},\overline {d})$
, and
![]() $\overline {d}=(\operatorname {\mathrm {id}},\overline {b})$
, where the lack of a symbol in front of the ordered pair indicates that
$\overline {d}=(\operatorname {\mathrm {id}},\overline {b})$
, where the lack of a symbol in front of the ordered pair indicates that
![]() $\overline {b}$
,
$\overline {b}$
,
![]() $\overline {c}$
, and
$\overline {c}$
, and
![]() $\overline {d}$
fix the children of the root. The Grigorchuk group was the first example of a finitely generated group that has intermediate growth, and that is amenable but not elementary amenable [Reference GrigorchukGri84].
$\overline {d}$
fix the children of the root. The Grigorchuk group was the first example of a finitely generated group that has intermediate growth, and that is amenable but not elementary amenable [Reference GrigorchukGri84].
2.1 Braiding groups of automorphisms
Now we describe a braided version of all of the above. Let
![]() $B_d$
be the d-strand braid group. Via the standard projection
$B_d$
be the d-strand braid group. Via the standard projection
![]() $B_d\to S_d$
, we get an action of
$B_d\to S_d$
, we get an action of
![]() $B_d$
on X. Hence, we can consider finitely iterated wreath products
$B_d$
on X. Hence, we can consider finitely iterated wreath products
![]() $B_d\wr _X^n B_d$
, take the projective limit, and get the infinitely iterated wreath product
$B_d\wr _X^n B_d$
, take the projective limit, and get the infinitely iterated wreath product
which we may also write as
![]() $B_d \wr _X^\infty B_d$
.
$B_d \wr _X^\infty B_d$
.
Definition 2.4 (Braided
 $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
)
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
)
Call the above infinitely iterated wreath product the braided automorphism group of
![]() $\mathcal {T}_d$
, denoted
$\mathcal {T}_d$
, denoted
Note that
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d) \cong B_d\wr _X \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, and so just like with
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d) \cong B_d\wr _X \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, and so just like with
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, we get a “braided wreath recursion”: any
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, we get a “braided wreath recursion”: any
![]() $f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
decomposes as
$f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
decomposes as
![]() $f=\phi (f)(f_1,\dots ,f_d)$
, where
$f=\phi (f)(f_1,\dots ,f_d)$
, where
is the natural epimorphism coming from the wreath product, and
![]() $f_i\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Also, note that the epimorphism
$f_i\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Also, note that the epimorphism
![]() $B_d\to S_d$
induces an epimorphism
$B_d\to S_d$
induces an epimorphism
For any
![]() $f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, define
$f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, define
where
![]() $f=\phi (f)(f_1,\dots ,f_d)$
is the braided wreath recursion. In particular, for any subgroup
$f=\phi (f)(f_1,\dots ,f_d)$
is the braided wreath recursion. In particular, for any subgroup
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the image
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the image
![]() $\psi (G)$
is a subset of
$\psi (G)$
is a subset of
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
. This leads us to the following.
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)^X$
. This leads us to the following.
Definition 2.5 (Braided self-similar)
A subgroup
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called braided self-similar if
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called braided self-similar if
![]() $\psi (G)\subseteq G^X$
.
$\psi (G)\subseteq G^X$
.
Definition 2.6 (Braided self-identical)
A subgroup
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called braided self-identical if
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
is called braided self-identical if
![]() $\psi (g)=(g,\dots ,g)$
for all
$\psi (g)=(g,\dots ,g)$
for all
![]() $g\in G$
.
$g\in G$
.
Note that the image in
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
under
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
under
![]() $\pi $
of any braided self-similar group is a self-similar group (with an analogous statement for self-identical).
$\pi $
of any braided self-similar group is a self-similar group (with an analogous statement for self-identical).
Remark 2.3 In terms of being able to construct these variants of self-similar groups, there is nothing particularly special about braid groups. More generally, given any group
![]() $\Gamma $
acting on any set Y, one can form the iterated wreath products
$\Gamma $
acting on any set Y, one can form the iterated wreath products
![]() $\Gamma \wr _Y^n \Gamma $
, take the projective limit to get
$\Gamma \wr _Y^n \Gamma $
, take the projective limit to get
![]() $\Gamma \wr _Y (\Gamma \wr _Y(\Gamma \wr _Y\cdots ))$
, and then consider subgroups G for which the associated wreath recursion of any element of G involves only elements of G. One could call these “
$\Gamma \wr _Y (\Gamma \wr _Y(\Gamma \wr _Y\cdots ))$
, and then consider subgroups G for which the associated wreath recursion of any element of G involves only elements of G. One could call these “
![]() $(\Gamma ,Y)$
-self-similar.” Our focus here is on braided versions, so we will not pursue this degree of generality here.
$(\Gamma ,Y)$
-self-similar.” Our focus here is on braided versions, so we will not pursue this degree of generality here.
Example 2.4 (Subgroups of the braid group)
This example is the “braided” version of Example 2.1. For
![]() $\beta \in B_d$
, we can define an element of
$\beta \in B_d$
, we can define an element of
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, also denoted
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, also denoted
![]() $\beta $
, via the braided wreath recursion
$\beta $
, via the braided wreath recursion
![]() $\beta =\beta (\beta ,\dots ,\beta )$
. In particular, viewing
$\beta =\beta (\beta ,\dots ,\beta )$
. In particular, viewing
![]() $B_d$
as a subgroup of
$B_d$
as a subgroup of
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, in this way, we see that
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, in this way, we see that
![]() $B_d$
, and indeed any subgroup of
$B_d$
, and indeed any subgroup of
![]() $B_d$
, is braided self-identical (hence braided self-similar).
$B_d$
, is braided self-identical (hence braided self-similar).
Before the next example, let us fix a generator
![]() $\zeta $
of
$\zeta $
of
![]() $B_2\cong \mathbb {Z}$
, which will also be useful in all that follows. We will use the braid where the strand on the left crosses over the strand on the right as the strands go down, as in Figure 1.
$B_2\cong \mathbb {Z}$
, which will also be useful in all that follows. We will use the braid where the strand on the left crosses over the strand on the right as the strands go down, as in Figure 1.

Figure 1: The braid
![]() $\zeta $
.
$\zeta $
.
Example 2.5 (
 $\mathbb {Z}\wr \mathbb {Z}$
)
$\mathbb {Z}\wr \mathbb {Z}$
)
As a nice example that is braided self-similar but not braided self-identical, we can use
![]() $\mathbb {Z}\wr \mathbb {Z}$
. Take elements a and b whose braided wreath recursions are
$\mathbb {Z}\wr \mathbb {Z}$
. Take elements a and b whose braided wreath recursions are
![]() $a=\zeta (1,a)$
and
$a=\zeta (1,a)$
and
![]() $b=\zeta ^2(1,b)$
. A computation shows that
$b=\zeta ^2(1,b)$
. A computation shows that
![]() $a^{2k}ba^{-2k}=\zeta ^2(1,a^k ba^{-k})$
and
$a^{2k}ba^{-2k}=\zeta ^2(1,a^k ba^{-k})$
and
![]() $a^{2k-1}ba^{-(2k-1)}=\zeta ^2(a^k ba^{-k},1)$
for all
$a^{2k-1}ba^{-(2k-1)}=\zeta ^2(a^k ba^{-k},1)$
for all
![]() $k\in \mathbb {Z}$
, so an induction argument shows that all the
$k\in \mathbb {Z}$
, so an induction argument shows that all the
![]() pairwise commute. Hence, we get a well-defined epimorphism
pairwise commute. Hence, we get a well-defined epimorphism
![]() $\mathbb {Z}\wr \mathbb {Z}\to \langle a,b\rangle $
, and we claim that it is an isomorphism. It suffices to show that if
$\mathbb {Z}\wr \mathbb {Z}\to \langle a,b\rangle $
, and we claim that it is an isomorphism. It suffices to show that if
![]() $(b_{i_1})^{p_1}\cdots (b_{i_\ell })^{p_\ell } a^q=1$
for
$(b_{i_1})^{p_1}\cdots (b_{i_\ell })^{p_\ell } a^q=1$
for
![]() $i_1<\cdots <i_\ell $
, then
$i_1<\cdots <i_\ell $
, then
![]() $p_1=\cdots =p_\ell =q=0$
. Hitting
$p_1=\cdots =p_\ell =q=0$
. Hitting
![]() $\langle a,b\rangle $
with
$\langle a,b\rangle $
with
![]() $\pi $
, since
$\pi $
, since
![]() $b\in \ker (\pi )$
and one can check that a maps under
$b\in \ker (\pi )$
and one can check that a maps under
![]() $\pi $
to an infinite order element of
$\pi $
to an infinite order element of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
, we see that
$\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
, we see that
![]() $q=0$
. Now, applying braided wreath recursions and using induction on the
$q=0$
. Now, applying braided wreath recursions and using induction on the
![]() $p_i$
, we see that the only possibility is
$p_i$
, we see that the only possibility is
![]() $p_1=\cdots =p_\ell =0$
, as desired.
$p_1=\cdots =p_\ell =0$
, as desired.
Before discussing our main example of the braided Grigorchuk group, let us pin down the kernel of the map
![]() $\pi \colon \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, i.e.,
$\pi \colon \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, i.e.,
![]() $\pi \colon B_d\wr _X^\infty B_d\to S_d\wr _X^\infty S_d$
. First, note that the kernel of
$\pi \colon B_d\wr _X^\infty B_d\to S_d\wr _X^\infty S_d$
. First, note that the kernel of
![]() $\pi \colon B_d\to S_d$
is the pure braid group
$\pi \colon B_d\to S_d$
is the pure braid group
![]() $PB_d$
. The action of
$PB_d$
. The action of
![]() $PB_d$
on X is trivial, so
$PB_d$
on X is trivial, so
![]() $PB_d \wr _X^n PB_d$
is simply a direct product of copies of
$PB_d \wr _X^n PB_d$
is simply a direct product of copies of
![]() $PB_d$
, namely
$PB_d$
, namely
![]() $1+d+d^2+\cdots +d^n$
many copies. This equals the kernel of the natural map
$1+d+d^2+\cdots +d^n$
many copies. This equals the kernel of the natural map
![]() $B_d \wr _X^n B_d \to S_d \wr _X^n S_d$
. Now we get the following.
$B_d \wr _X^n B_d \to S_d \wr _X^n S_d$
. Now we get the following.
Lemma 2.6 The kernel of
![]() $\pi \colon B_d\wr _X^\infty B_d\to S_d\wr _X^\infty S_d$
is
$\pi \colon B_d\wr _X^\infty B_d\to S_d\wr _X^\infty S_d$
is
![]() $PB_d\wr _X^\infty PB_d$
, which is a direct product of infinitely many copies of
$PB_d\wr _X^\infty PB_d$
, which is a direct product of infinitely many copies of
![]() $PB_d$
.
$PB_d$
.
Proof Viewing the projective limit
![]() $B_d\wr _X^\infty B_d$
as a subgroup of the direct product of the factors
$B_d\wr _X^\infty B_d$
as a subgroup of the direct product of the factors
![]() $B_d \wr _X^n B_d$
in the projective system, and similarly
$B_d \wr _X^n B_d$
in the projective system, and similarly
![]() $S_d\wr _X^\infty S_d$
as a subgroup of the direct product of the
$S_d\wr _X^\infty S_d$
as a subgroup of the direct product of the
![]() $S_d \wr _X^n S_d$
, the map
$S_d \wr _X^n S_d$
, the map
![]() $\pi $
is the restriction of the analogous map between these direct products. The kernel of the map on the direct products is clearly the direct product of the
$\pi $
is the restriction of the analogous map between these direct products. The kernel of the map on the direct products is clearly the direct product of the
![]() $PB_d \wr _X^n PB_d$
. This shows that the kernel of
$PB_d \wr _X^n PB_d$
. This shows that the kernel of
![]() $\pi $
is the intersection of
$\pi $
is the intersection of
![]() $B_d\wr _X^\infty B_d$
with the direct product of the
$B_d\wr _X^\infty B_d$
with the direct product of the
![]() $PB_d \wr _X^n PB_d$
, which is
$PB_d \wr _X^n PB_d$
, which is
![]() $PB_d\wr _X^\infty PB_d$
. Since
$PB_d\wr _X^\infty PB_d$
. Since
![]() $PB_d$
acts trivially on X, this is just a direct product of copies of
$PB_d$
acts trivially on X, this is just a direct product of copies of
![]() $PB_d$
.
$PB_d$
.
Corollary 2.7 The kernel of
![]() $\pi \colon \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
is abelian.
$\pi \colon \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
is abelian.
Proof By Lemma 2.6, the kernel is a direct product of copies of
![]() $PB_2\cong \mathbb {Z}$
.
$PB_2\cong \mathbb {Z}$
.
2.2 The braided Grigorchuk group
Now we construct a braided version of
![]() $\operatorname {\mathrm {Grig}}$
. Denote by a the element of
$\operatorname {\mathrm {Grig}}$
. Denote by a the element of
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
defined by the braided wreath recursion
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
defined by the braided wreath recursion
![]() $a=\zeta (1,1)$
. Now define b, c, and d via the braided wreath recursions
$a=\zeta (1,1)$
. Now define b, c, and d via the braided wreath recursions
![]() $b=(a,c)$
,
$b=(a,c)$
,
![]() $c=(a^{-1},d)$
, and
$c=(a^{-1},d)$
, and
![]() $d=(1,b)$
.
$d=(1,b)$
.
Definition 2.7 (Braided Grigorchuk group)
The braided Grigorchuk group
![]() $\operatorname {\mathrm {brGrig}}$
is the subgroup of
$\operatorname {\mathrm {brGrig}}$
is the subgroup of
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
defined by
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
defined by
The reason for using
![]() $c=(a^{-1},d)$
rather than
$c=(a^{-1},d)$
rather than
![]() $c=(a,d)$
is so that we get the pleasant-looking relation
$c=(a,d)$
is so that we get the pleasant-looking relation
![]() $bcd=1$
that holds analogously in the Grigorchuk group, as the proof of the next result shows.
$bcd=1$
that holds analogously in the Grigorchuk group, as the proof of the next result shows.
Lemma 2.8 The subgroup
![]() $\langle b,c,d\rangle $
of
$\langle b,c,d\rangle $
of
![]() $\operatorname {\mathrm {brGrig}}$
is isomorphic to
$\operatorname {\mathrm {brGrig}}$
is isomorphic to
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Proof First, we claim that
![]() $bcd=1$
. Applying braided wreath recursions to
$bcd=1$
. Applying braided wreath recursions to
![]() $bcd$
produces
$bcd$
produces
![]() $(1,cdb)$
, then
$(1,cdb)$
, then
![]() $(1,(1,dbc))$
, and so forth, which shows that indeed
$(1,(1,dbc))$
, and so forth, which shows that indeed
![]() $bcd=1$
. A similar argument shows
$bcd=1$
. A similar argument shows
![]() $cbd=1$
. In particular, b and c commute and
$cbd=1$
. In particular, b and c commute and
![]() $d=(bc)^{-1}$
. It remains to show that b and c admit no nontrivial relations of the form
$d=(bc)^{-1}$
. It remains to show that b and c admit no nontrivial relations of the form
![]() $b^k c^\ell =1$
. Applying braided wreath recursions, we get
$b^k c^\ell =1$
. Applying braided wreath recursions, we get
![]() $b^k c^\ell = (a^{k+\ell },(a^k,d^k b^\ell ))$
, which equals
$b^k c^\ell = (a^{k+\ell },(a^k,d^k b^\ell ))$
, which equals
![]() $1$
only if
$1$
only if
![]() $k+\ell =0$
and
$k+\ell =0$
and
![]() $k=0$
, so indeed no nontrivial such relations hold.
$k=0$
, so indeed no nontrivial such relations hold.
Lemma 2.9 The restriction of
![]() $\pi\, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
to
$\pi\, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
to
![]() $\operatorname {\mathrm {brGrig}}$
yields an epimorphism from
$\operatorname {\mathrm {brGrig}}$
yields an epimorphism from
![]() $\operatorname {\mathrm {brGrig}}$
onto
$\operatorname {\mathrm {brGrig}}$
onto
![]() $\operatorname {\mathrm {Grig}}$
.
$\operatorname {\mathrm {Grig}}$
.
Proof First, note that
![]() $\pi\, {\colon}\, B_2\to S_2$
sends
$\pi\, {\colon}\, B_2\to S_2$
sends
![]() $\zeta $
to
$\zeta $
to
![]() $(1~2)$
. Thus,
$(1~2)$
. Thus,
![]() $\pi\, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
sends a to the element
$\pi\, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
sends a to the element
![]() $\overline {a}$
of
$\overline {a}$
of
![]() $\operatorname {\mathrm {Grig}}$
. It follows immediately that b, c, and d, respectively, map under
$\operatorname {\mathrm {Grig}}$
. It follows immediately that b, c, and d, respectively, map under
![]() $\pi $
to
$\pi $
to
![]() $\overline {b}$
,
$\overline {b}$
,
![]() $\overline {c}$
, and
$\overline {c}$
, and
![]() $\overline {d}$
.
$\overline {d}$
.
Corollary 2.10 The braided Grigorchuk group
![]() $\operatorname {\mathrm {brGrig}}$
is amenable.
$\operatorname {\mathrm {brGrig}}$
is amenable.
Proof By Lemma 2.9, we have an epimorphism
![]() $\pi\, {\colon}\, \operatorname{\mathrm {brGrig}}\to \operatorname {\mathrm {Grig}}$
. The kernel is abelian by Corollary 2.7. Hence,
$\pi\, {\colon}\, \operatorname{\mathrm {brGrig}}\to \operatorname {\mathrm {Grig}}$
. The kernel is abelian by Corollary 2.7. Hence,
![]() $\operatorname {\mathrm {brGrig}}$
is abelian-by-amenable, so amenable.
$\operatorname {\mathrm {brGrig}}$
is abelian-by-amenable, so amenable.
Momentarily, we will prove that the braided Grigorchuk group is not finitely presented. The proof is inspired by the proof for the Grigorchuk group with some modifications, and we (roughly) follow this proof as given in [Reference DehornoydlH00]. First, we need some setup.
By Lemma 2.8, we see that there is a canonical epimorphism from
![]() onto
onto
![]() $\operatorname {\mathrm {brGrig}}$
by mapping the generator of the first copy of
$\operatorname {\mathrm {brGrig}}$
by mapping the generator of the first copy of
![]() $\mathbb {Z}$
to a and mapping the generators of
$\mathbb {Z}$
to a and mapping the generators of
![]() $\mathbb {Z}^2$
to b and c. Thus any element in
$\mathbb {Z}^2$
to b and c. Thus any element in
![]() $\operatorname {\mathrm {brGrig}}$
can be written (non-uniquely) as
$\operatorname {\mathrm {brGrig}}$
can be written (non-uniquely) as
where the
![]() $z_i$
are of the form
$z_i$
are of the form
![]() $b^{m_i}c^{n_i}$
for some
$b^{m_i}c^{n_i}$
for some
![]() $m_i, n_i \in \mathbb {Z}$
and are nontrivial except possibly when
$m_i, n_i \in \mathbb {Z}$
and are nontrivial except possibly when
![]() $i=1$
or
$i=1$
or
![]() $\ell +1$
. Call an expression of this form reduced. For a reduced expression as above, declare the length, denoted
$\ell +1$
. Call an expression of this form reduced. For a reduced expression as above, declare the length, denoted
![]() $|z_1a^{k_1}z_2\cdots a^{k_\ell }z_{\ell +1}|$
, to be the number of terms in the alternating product, so the length is
$|z_1a^{k_1}z_2\cdots a^{k_\ell }z_{\ell +1}|$
, to be the number of terms in the alternating product, so the length is
![]() $2\ell -1$
,
$2\ell -1$
,
![]() $2\ell $
, or
$2\ell $
, or
![]() $2\ell +1$
depending on whether
$2\ell +1$
depending on whether
![]() $z_1$
and/or
$z_1$
and/or
![]() $z_{\ell +1}$
are equal to
$z_{\ell +1}$
are equal to
![]() $1$
. Similarly, define
$1$
. Similarly, define
![]() $|z_1a^{k_1}z_2\cdots a^{k_\ell }z_{\ell +1}|_a=\sum _{i=1}^\ell k_i$
, i.e., the sum of the exponents on the a terms.
$|z_1a^{k_1}z_2\cdots a^{k_\ell }z_{\ell +1}|_a=\sum _{i=1}^\ell k_i$
, i.e., the sum of the exponents on the a terms.
Given any word w in the generators a, b, c, and d and their inverses, one can obtain a new word in reduced form by iteratively applying the following reductions and the analogous ones for their inverses:
-
(1)
 $g^ig^j=g^{i+j}$
for
$g^ig^j=g^{i+j}$
for
 $g\in \{a,b, c, d\}.$
$g\in \{a,b, c, d\}.$
-
(2)
 $d^{-1}=bc.$
$d^{-1}=bc.$
-
(3)
 $cb=bc.$
$cb=bc.$
Call the resulting word
![]() $w^{\mathrm{red}}$
.
$w^{\mathrm{red}}$
.
Lemma 2.11 Let w be a reduced expression for an element of
![]() $\operatorname {\mathrm {brGrig}}$
. Consider the braided wreath recursion
$\operatorname {\mathrm {brGrig}}$
. Consider the braided wreath recursion
![]() $w=\phi (w)(w_1, w_2)$
. Then
$w=\phi (w)(w_1, w_2)$
. Then
Proof Using the braided wreath recursion and applying the reductions, we get
 $$\begin{align*}(b^kc^m)a^n= \begin{cases} \zeta^n(a^{k-m}, b^{-m}c^{k-m}), & \text{ if } n \text{ is even,} \\ \zeta^n(b^{-m}c^{k-m}, a^{k-m}), & \text{ if } n \text{ is odd.} \end{cases} \end{align*}$$
$$\begin{align*}(b^kc^m)a^n= \begin{cases} \zeta^n(a^{k-m}, b^{-m}c^{k-m}), & \text{ if } n \text{ is even,} \\ \zeta^n(b^{-m}c^{k-m}, a^{k-m}), & \text{ if } n \text{ is odd.} \end{cases} \end{align*}$$
Thus, each pair
![]() $z_i a^{k_i}$
in the alternating product contributes at most one term to
$z_i a^{k_i}$
in the alternating product contributes at most one term to
![]() $w_1$
and at most one term to
$w_1$
and at most one term to
![]() $w_2$
. The result now follows.
$w_2$
. The result now follows.
Lemma 2.12 The braided Grigorchuk group has solvable word problem.
Proof Let w be an expression in reduced form. To decide if w represents the identity, proceed as follows.
-
(1) Determine if
 $|w|_a= 0$
.
$|w|_a= 0$
.-
(a) If
 $|w|_a \ne 0$
, then
$|w|_a \ne 0$
, then
 $w\ne 1.$
$w\ne 1.$
-
(b) If
 $|w|_a=0$
and the length of w is
$|w|_a=0$
and the length of w is
 $0$
, then
$0$
, then
 $w=1$
.
$w=1$
. -
(c) If
 $|w|_a=0$
and the length of w is at least 1, then apply
$|w|_a=0$
and the length of w is at least 1, then apply
 $\psi $
to obtain
$\psi $
to obtain
 $\psi (w)=(w_1, w_2)$
and go to
$\psi (w)=(w_1, w_2)$
and go to
 $(ii).$
$(ii).$
-
-
(2) Compute
 $w_1^{\mathrm{red}}$
and
$w_1^{\mathrm{red}}$
and
 $w_2^{\mathrm{red}}$
and return to
$w_2^{\mathrm{red}}$
and return to
 $(i)$
which should be checked for both
$(i)$
which should be checked for both
 $w_1^{\mathrm{red}}$
and
$w_1^{\mathrm{red}}$
and
 $w_2^{\mathrm{red}}$
.
$w_2^{\mathrm{red}}$
.
It follows from Lemma 2.11 that the procedure terminates.
Let
![]() $W^{\mathrm{red}}$
be the set of reduced words, so we can identify
$W^{\mathrm{red}}$
be the set of reduced words, so we can identify
![]() $W^{\mathrm{red}}$
with
$W^{\mathrm{red}}$
with
![]() $F=\mathbb {Z} \ast \mathbb {Z}^2$
. For
$F=\mathbb {Z} \ast \mathbb {Z}^2$
. For
![]() $w\in W^{\mathrm{red}}$
and for
$w\in W^{\mathrm{red}}$
and for
![]() $j_1, \dots , j_n\in \{1,2\}$
, let
$j_1, \dots , j_n\in \{1,2\}$
, let
![]() $w_{j_1\cdots j_n}^{\mathrm{red}}$
denote the reduced word defined inductively by
$w_{j_1\cdots j_n}^{\mathrm{red}}$
denote the reduced word defined inductively by
Let
![]() $\Psi\, {\colon}\, F\rightarrow \operatorname {\mathrm {brGrig}}$
be the canonical epimorphism.
$\Psi\, {\colon}\, F\rightarrow \operatorname {\mathrm {brGrig}}$
be the canonical epimorphism.
Definition 2.8 For each
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $K_n$
denote the subset of F given by
$K_n$
denote the subset of F given by
Lemma 2.13 We have
![]() $\{1\}=K_0\leq K_1 \leq K_2\leq \cdots \leq \bigcup \limits _{n=0}^\infty K_n=\ker {\Psi }$
. Moreover, each
$\{1\}=K_0\leq K_1 \leq K_2\leq \cdots \leq \bigcup \limits _{n=0}^\infty K_n=\ker {\Psi }$
. Moreover, each
![]() $K_n$
is normal in F and all the inclusions are strict.
$K_n$
is normal in F and all the inclusions are strict.
Proof It is clear that
![]() $K_n\leq K_{n+1}$
. The fact that
$K_n\leq K_{n+1}$
. The fact that
![]() $\bigcup \limits _{n=0}^\infty K_n=\ker {\Psi }$
follows from the fact that the procedure in Lemma 2.12 terminates. It remains to show that each
$\bigcup \limits _{n=0}^\infty K_n=\ker {\Psi }$
follows from the fact that the procedure in Lemma 2.12 terminates. It remains to show that each
![]() $K_n$
is normal and that the inclusions are strict.
$K_n$
is normal and that the inclusions are strict.
It is clear that
![]() $K_0$
is normal in F and so we proceed by induction. Observe that
$K_0$
is normal in F and so we proceed by induction. Observe that
Let
![]() $w\in K_n$
. We claim that any conjugate of w by one of the generators is again in
$w\in K_n$
. We claim that any conjugate of w by one of the generators is again in
![]() $K_n.$
For
$K_n.$
For
![]() $a^{-1}wa$
, this follows from the fact that
$a^{-1}wa$
, this follows from the fact that
![]() $|a^{-1}wa|_a=|w|_a$
and that
$|a^{-1}wa|_a=|w|_a$
and that
![]() $(a^{-1}wa)_1=w_2$
and
$(a^{-1}wa)_1=w_2$
and
![]() $(a^{-1}wa)_2=w_1$
. For the remaining cases, we see that
$(a^{-1}wa)_2=w_1$
. For the remaining cases, we see that
![]() $|b^{-1}wb|_a=|c^{-1}wc|_a=|d^{-1}wd|_a=|w|_a$
, and moreover
$|b^{-1}wb|_a=|c^{-1}wc|_a=|d^{-1}wd|_a=|w|_a$
, and moreover
Now normality follows from the induction hypothesis.
Finally, we verify that the inclusions are proper. Let
![]() $\sigma $
be the endomorphism of F defined by
$\sigma $
be the endomorphism of F defined by
![]() $\sigma (a)=a^{-1}c^{-1}a, \sigma (b)=d, \sigma (c)=b,$
and
$\sigma (a)=a^{-1}c^{-1}a, \sigma (b)=d, \sigma (c)=b,$
and
![]() $\sigma (d)=c$
. Observe that
$\sigma (d)=c$
. Observe that
![]() $\sigma $
takes reduced words to reduced words, and moreover if
$\sigma $
takes reduced words to reduced words, and moreover if
![]() $|w|_a=0$
then
$|w|_a=0$
then
![]() $|\sigma (w)|_a=0$
. Also, note that
$|\sigma (w)|_a=0$
. Also, note that
![]() $\sigma (a)_1=d^{-1}$
,
$\sigma (a)_1=d^{-1}$
,
![]() $\sigma (d)_1=a^{-1}$
,
$\sigma (d)_1=a^{-1}$
,
![]() $\sigma (a)_2=a$
, and
$\sigma (a)_2=a$
, and
![]() $\sigma (d)_2=d$
. Now fix
$\sigma (d)_2=d$
. Now fix
and
We claim that
![]() $\sigma ^n(w)$
and
$\sigma ^n(w)$
and
![]() $\sigma ^n(\widetilde {w})$
are in
$\sigma ^n(\widetilde {w})$
are in
![]() $K_{n+1}$
but not
$K_{n+1}$
but not
![]() $K_n$
. For the base cases, one easily checks that w and
$K_n$
. For the base cases, one easily checks that w and
![]() $\widetilde {w}$
are both in
$\widetilde {w}$
are both in
![]() $K_1$
but not in
$K_1$
but not in
![]() $K_0$
. Now note that
$K_0$
. Now note that
![]() $\sigma (w)_1=\widetilde {w}$
,
$\sigma (w)_1=\widetilde {w}$
,
![]() $\sigma (w)_2=w$
,
$\sigma (w)_2=w$
,
![]() $\sigma (\widetilde {w})_1=w$
, and
$\sigma (\widetilde {w})_1=w$
, and
![]() $\sigma (\widetilde {w})_2=\widetilde {w}$
, so using the base case, we get that
$\sigma (\widetilde {w})_2=\widetilde {w}$
, so using the base case, we get that
![]() $\sigma (w)$
and
$\sigma (w)$
and
![]() $\sigma (\widetilde {w})$
are both in
$\sigma (\widetilde {w})$
are both in
![]() $K_2$
but not
$K_2$
but not
![]() $K_1$
. Continuing in this way, the result follows by induction.
$K_1$
. Continuing in this way, the result follows by induction.
Proposition 2.14 The braided Grigorchuk group
![]() $\operatorname {\mathrm {brGrig}}$
is not finitely presented.
$\operatorname {\mathrm {brGrig}}$
is not finitely presented.
Proof Suppose
![]() $\operatorname {\mathrm {brGrig}}$
is finitely presented. As it is a quotient of F, it has a presentation of the form
$\operatorname {\mathrm {brGrig}}$
is finitely presented. As it is a quotient of F, it has a presentation of the form
giving
![]() $\operatorname {\mathrm {brGrig}}\cong F/R$
where
$\operatorname {\mathrm {brGrig}}\cong F/R$
where
![]() $R=\ker (\Psi )$
is the normal closure of
$R=\ker (\Psi )$
is the normal closure of
![]() $r_1, \dots , r_k$
in F. As each
$r_1, \dots , r_k$
in F. As each
![]() $r_i$
is contained in some
$r_i$
is contained in some
![]() $K_n$
, this contradicts Lemma 2.13.
$K_n$
, this contradicts Lemma 2.13.
Anthony Genevois has pointed out to us that Proposition 2.14 also follows from [Reference Bestvina and BradyBGdlH13, Theorem 1.6], which implies that no finitely presented amenable group has
![]() $\operatorname {\mathrm {Grig}}$
as a quotient.
$\operatorname {\mathrm {Grig}}$
as a quotient.
Remark 2.15 Our braided Grigorchuk group
![]() $\operatorname {\mathrm {brGrig}}$
is similar to the torsion-free group of intermediate growth constructed by Grigorchuk in [Reference GrigorchukGri85, Section 5]; see [Reference AllcockAll21] for a similar construction (which in discussions with Daniel Allcock we have determined is isomorphic to the group in [Reference GrigorchukGri85]). The difference is that, phrased in our language, it seems likely that that group would use the braided wreath recursions
$\operatorname {\mathrm {brGrig}}$
is similar to the torsion-free group of intermediate growth constructed by Grigorchuk in [Reference GrigorchukGri85, Section 5]; see [Reference AllcockAll21] for a similar construction (which in discussions with Daniel Allcock we have determined is isomorphic to the group in [Reference GrigorchukGri85]). The difference is that, phrased in our language, it seems likely that that group would use the braided wreath recursions
![]() $b=(a,c)$
,
$b=(a,c)$
,
![]() $c=(a,d)$
, and
$c=(a,d)$
, and
![]() $d=(1,b)$
. We chose
$d=(1,b)$
. We chose
![]() $c=(a^{-1},d)$
so that we would get
$c=(a^{-1},d)$
so that we would get
![]() $bcd=1$
, which makes
$bcd=1$
, which makes
![]() $\operatorname {\mathrm {brGrig}}$
feel more closely related to
$\operatorname {\mathrm {brGrig}}$
feel more closely related to
![]() $\operatorname {\mathrm {Grig}}$
. We will leave it as a question for future investigation whether
$\operatorname {\mathrm {Grig}}$
. We will leave it as a question for future investigation whether
![]() $\operatorname {\mathrm {brGrig}}$
is isomorphic to the group from [Reference AllcockAll21, Reference GrigorchukGri85], and so in particular whether
$\operatorname {\mathrm {brGrig}}$
is isomorphic to the group from [Reference AllcockAll21, Reference GrigorchukGri85], and so in particular whether
![]() $\operatorname {\mathrm {brGrig}}$
has intermediate growth.
$\operatorname {\mathrm {brGrig}}$
has intermediate growth.
3 Braiding groups of almost-automorphisms of trees
In this section, we discuss groups of almost-automorphisms of trees, and introduce braided versions. We will use the framework of d-ary cloning systems from [Reference SteinSZ21], which generalize cloning systems from [Reference Witzel and ZaremskyWZ18]. Very loosely, d-ary cloning systems provide a way to construct new Thompson-like groups, and have proved useful in a variety of recent work, for example, on decision problems [Reference Bux, Fluch, Marschler, Witzel and ZaremskyBZFG+18], orderability [Reference IshidaIsh18], von Neumann algebras [Reference Brown and GeogheganBZ], and the so-called Jones technology [Reference BrownBro21]. Let us recall the relevant background.
3.1 Cloning systems
Definition 3.1 (d-ary cloning system)
Let
![]() $d\ge 2$
be an integer, and let
$d\ge 2$
be an integer, and let
![]() $(G_n)_{n\in \mathbb {N}}$
be a family of groups. For each
$(G_n)_{n\in \mathbb {N}}$
be a family of groups. For each
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\rho _n\, {\colon}\, G_n\to S_n$
be a homomorphism to the symmetric group
$\rho _n\, {\colon}\, G_n\to S_n$
be a homomorphism to the symmetric group
![]() $S_n$
, called a representation map. For each
$S_n$
, called a representation map. For each
![]() $1\le k\le n$
, let
$1\le k\le n$
, let
![]() $\kappa _k^n\, {\colon}\, G_n \to G_{n+d-1}$
be an injective function (not necessarily a homomorphism), called a d-ary cloning map. We write
$\kappa _k^n\, {\colon}\, G_n \to G_{n+d-1}$
be an injective function (not necessarily a homomorphism), called a d-ary cloning map. We write
![]() $\rho _n$
to the left of its input and
$\rho _n$
to the left of its input and
![]() $\kappa _k^n$
to the right of its input, for reasons of visual clarity. Now we call the triple
$\kappa _k^n$
to the right of its input, for reasons of visual clarity. Now we call the triple
a d-ary cloning system if the following axioms hold: (C1): (Cloning a product)
![]() $(gh)\kappa _k^n = (g)\kappa _{\rho _n(h)k}^{n} (h)\kappa _k^n$
. (C2): (Product of clonings)
$(gh)\kappa _k^n = (g)\kappa _{\rho _n(h)k}^{n} (h)\kappa _k^n$
. (C2): (Product of clonings)
![]() $\kappa _\ell ^n \circ \kappa _k^{n+d-1} = \kappa _k^n \circ \kappa _{\ell +d-1}^{n+d-1}$
. (C3): (Compatibility)
$\kappa _\ell ^n \circ \kappa _k^{n+d-1} = \kappa _k^n \circ \kappa _{\ell +d-1}^{n+d-1}$
. (C3): (Compatibility)
![]() $\rho _{n+d-1}((g)\kappa _k^n)(i) = (\rho _n(g))\varsigma _k^n(i)$
for all
$\rho _{n+d-1}((g)\kappa _k^n)(i) = (\rho _n(g))\varsigma _k^n(i)$
for all
![]() $i\ne k,k+1,\dots ,k+d-1$
.
$i\ne k,k+1,\dots ,k+d-1$
.
Here, we always have
![]() $1\le k<\ell \le n$
and
$1\le k<\ell \le n$
and
![]() $g,h\in G_n$
, and
$g,h\in G_n$
, and
![]() $\varsigma _k^n$
denotes the standard d-ary cloning maps for the symmetric groups.
$\varsigma _k^n$
denotes the standard d-ary cloning maps for the symmetric groups.
The maps
![]() $\varsigma _k^n$
are explained in [Reference SteinSZ21, Example 2.2], and we will review them in Example 3.2.
$\varsigma _k^n$
are explained in [Reference SteinSZ21, Example 2.2], and we will review them in Example 3.2.
Remark 3.1 For an illustration of a cloning map in the special case
![]() $G_n=\operatorname {br}\!W_n$
(defined in Section 3.3), we direct the reader to Figure 2.
$G_n=\operatorname {br}\!W_n$
(defined in Section 3.3), we direct the reader to Figure 2.

Figure 2: An example of
![]() $2$
-ary cloning on
$2$
-ary cloning on
![]() $\operatorname {br}\!W_2$
. Here,
$\operatorname {br}\!W_2$
. Here,
![]() $f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
satisfies the braided wreath recursion
$f\in \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_2)$
satisfies the braided wreath recursion
![]() $f=\zeta (f,f)$
. The picture shows that
$f=\zeta (f,f)$
. The picture shows that
![]() $(\zeta (\operatorname {\mathrm {id}},f))\kappa _2^2 = (\zeta )\vartheta _2^2\phi ^{(2)}(f)(\operatorname {\mathrm {id}},f,f)$
. We use thick lines to indicate the strand getting cloned and the resulting strands.
$(\zeta (\operatorname {\mathrm {id}},f))\kappa _2^2 = (\zeta )\vartheta _2^2\phi ^{(2)}(f)(\operatorname {\mathrm {id}},f,f)$
. We use thick lines to indicate the strand getting cloned and the resulting strands.
Given a d-ary cloning system on a family of groups
![]() $(G_n)_{n\in \mathbb {N}}$
, one gets a Thompson-like group, denoted
$(G_n)_{n\in \mathbb {N}}$
, one gets a Thompson-like group, denoted
![]() $\mathscr {T}_d(G_*)$
, which can be viewed as a sort of “Thompson limit” of the
$\mathscr {T}_d(G_*)$
, which can be viewed as a sort of “Thompson limit” of the
![]() $G_n$
. Let us recall the construction of
$G_n$
. Let us recall the construction of
![]() $\mathscr {T}_d(G_*)$
. First, a d-ary tree is a finite rooted tree in which each nonleaf vertex has d children, and a d-ary caret is a d-ary tree with d leaves. An element of
$\mathscr {T}_d(G_*)$
. First, a d-ary tree is a finite rooted tree in which each nonleaf vertex has d children, and a d-ary caret is a d-ary tree with d leaves. An element of
![]() $\mathscr {T}_d(G_*)$
is represented by a triple
$\mathscr {T}_d(G_*)$
is represented by a triple
![]() $(T_-,g,T_+)$
where
$(T_-,g,T_+)$
where
![]() $T_\pm $
are d-ary trees with the same number of leaves, say n, and g is an element of
$T_\pm $
are d-ary trees with the same number of leaves, say n, and g is an element of
![]() $G_n$
. There is an equivalence relation on such triples, and the equivalence classes are the elements of
$G_n$
. There is an equivalence relation on such triples, and the equivalence classes are the elements of
![]() $\mathscr {T}_d(G_*)$
. The equivalence relation is given by expansion and reduction: an expansion of
$\mathscr {T}_d(G_*)$
. The equivalence relation is given by expansion and reduction: an expansion of
![]() $(T_-,g,T_+)$
is a triple of the form
$(T_-,g,T_+)$
is a triple of the form
![]() $(T_-',(g)\kappa _k^n,T_+')$
where
$(T_-',(g)\kappa _k^n,T_+')$
where
![]() $T_+'$
is
$T_+'$
is
![]() $T_+$
with a d-ary caret added to the kth leaf and
$T_+$
with a d-ary caret added to the kth leaf and
![]() $T_-'$
is
$T_-'$
is
![]() $T_-$
with a d-ary caret added to the
$T_-$
with a d-ary caret added to the
![]() $\rho _n(g)(k)$
th leaf. A reduction is the reverse of an expansion. Now declare that two triples are equivalent if we can get from one to the other via a finite sequence of expansions and reductions, and write
$\rho _n(g)(k)$
th leaf. A reduction is the reverse of an expansion. Now declare that two triples are equivalent if we can get from one to the other via a finite sequence of expansions and reductions, and write
![]() $[T_-,g,T_+]$
for the equivalence class of
$[T_-,g,T_+]$
for the equivalence class of
![]() $(T_-,g,T_+)$
.
$(T_-,g,T_+)$
.
Definition 3.2 (Thompson-like group)
The Thompson-like group
![]() $\mathscr {T}_d(G_*)$
is the set of equivalence classes
$\mathscr {T}_d(G_*)$
is the set of equivalence classes
![]() $[T_-,g,T_+]$
.
$[T_-,g,T_+]$
.
We have not explained the group operation on
![]() $\mathscr {T}_d(G_*)$
. The idea is that given any two elements
$\mathscr {T}_d(G_*)$
. The idea is that given any two elements
![]() $[T_-,g,T_+]$
and
$[T_-,g,T_+]$
and
![]() $[U_-,h,U_+]$
, up to expansions, we can assume that
$[U_-,h,U_+]$
, up to expansions, we can assume that
![]() ${T_+=U_-}$
. This is because any pair of d-ary trees have a common d-ary tree obtainable from either of them by adding d-ary carets to their leaves. Now the group operation on
${T_+=U_-}$
. This is because any pair of d-ary trees have a common d-ary tree obtainable from either of them by adding d-ary carets to their leaves. Now the group operation on
![]() $\mathscr {T}_d(G_*)$
is defined by
$\mathscr {T}_d(G_*)$
is defined by
when
![]() $T_+=U_-$
. The cloning axioms ensure that this is a well-defined group operation. The identity is
$T_+=U_-$
. The cloning axioms ensure that this is a well-defined group operation. The identity is
![]() $[T,1,T]$
(for any T) and inverses are given by
$[T,1,T]$
(for any T) and inverses are given by
![]() $[T_-,g,T_+]^{-1} = [T_+,g^{-1},T_-]$
.
$[T_-,g,T_+]^{-1} = [T_+,g^{-1},T_-]$
.
Example 3.2 (Cloning permutations)
The most fundamental example of a d-ary cloning system is on the family
![]() $(S_n)_{n\in \mathbb {N}}$
of symmetric groups. Take
$(S_n)_{n\in \mathbb {N}}$
of symmetric groups. Take
![]() $\rho _n \, {\colon}\, S_n\to S_n$
to be the identity, and let
$\rho _n \, {\colon}\, S_n\to S_n$
to be the identity, and let
be the function described as follows. Visualize
![]() $\sigma \in S_n$
by drawing arrows going up, from a line of labels
$\sigma \in S_n$
by drawing arrows going up, from a line of labels
![]() $1$
to n for the domain to another line of labels
$1$
to n for the domain to another line of labels
![]() $1$
to n for the range, with an arrow from i to
$1$
to n for the range, with an arrow from i to
![]() $\sigma (i)$
for each i. Now
$\sigma (i)$
for each i. Now
![]() $(\sigma )\varsigma _k^n \in S_{n+d-1}$
is obtained by replacing the arrow from k to
$(\sigma )\varsigma _k^n \in S_{n+d-1}$
is obtained by replacing the arrow from k to
![]() $\sigma (k)$
by d parallel arrows, and relabeling everything appropriately. For a (complicated) rigorous formula, see [Reference SteinSZ21, Example 2.2]. It turns out that this defines a d-ary cloning system, with d-ary cloning maps
$\sigma (k)$
by d parallel arrows, and relabeling everything appropriately. For a (complicated) rigorous formula, see [Reference SteinSZ21, Example 2.2]. It turns out that this defines a d-ary cloning system, with d-ary cloning maps
![]() $\varsigma _k^n$
. The Thompson-like group
$\varsigma _k^n$
. The Thompson-like group
![]() $\mathscr {T}_d(S_*)$
that arises from this d-ary cloning system is (isomorphic to) the Higman–Thompson group
$\mathscr {T}_d(S_*)$
that arises from this d-ary cloning system is (isomorphic to) the Higman–Thompson group
![]() $V_d$
.
$V_d$
.
Example 3.3 (Cloning braids)
The braided version of the above example is a d-ary cloning system on the family
![]() $(B_n)_{n\in \mathbb {N}}$
of braid groups. Take
$(B_n)_{n\in \mathbb {N}}$
of braid groups. Take
![]() $\rho _n\, {\colon}\, B_n\to S_n$
to be the natural projection of
$\rho _n\, {\colon}\, B_n\to S_n$
to be the natural projection of
![]() $B_n$
onto
$B_n$
onto
![]() $S_n$
, and let
$S_n$
, and let
be the function described as follows. Visualize
![]() $\beta \in B_n$
as an n-strand braid diagram, counting the strands
$\beta \in B_n$
as an n-strand braid diagram, counting the strands
![]() $1$
to n at the bottom. Now
$1$
to n at the bottom. Now
![]() $(\beta )\vartheta _k^n \in B_{n+d-1}$
is obtained by replacing the kth strand (counting at the bottom) by d parallel strands. As discussed in [Reference Witzel and ZaremskyWZ18, Remark 2.10], in the
$(\beta )\vartheta _k^n \in B_{n+d-1}$
is obtained by replacing the kth strand (counting at the bottom) by d parallel strands. As discussed in [Reference Witzel and ZaremskyWZ18, Remark 2.10], in the
![]() $d=2$
case, this really defines a cloning system (this was essentially already shown by Brin in [Reference BrinBri07], before cloning systems had been introduced, using the language of Zappa–Szép products), and it is easy to see that in the arbitrary d case, it defines a d-ary cloning system. The Thompson-like group
$d=2$
case, this really defines a cloning system (this was essentially already shown by Brin in [Reference BrinBri07], before cloning systems had been introduced, using the language of Zappa–Szép products), and it is easy to see that in the arbitrary d case, it defines a d-ary cloning system. The Thompson-like group
![]() $\mathscr {T}_d(B_*)$
that arises from this d-ary cloning system is (isomorphic to) the braided Higman–Thompson group
$\mathscr {T}_d(B_*)$
that arises from this d-ary cloning system is (isomorphic to) the braided Higman–Thompson group
![]() $\operatorname {br}\!V_d$
, considered previously by Aroca and Cumplido in [Reference AllcockAC22], and the first author and Wu in [Reference Skipper and ZaremskySW].
$\operatorname {br}\!V_d$
, considered previously by Aroca and Cumplido in [Reference AllcockAC22], and the first author and Wu in [Reference Skipper and ZaremskySW].
3.2 Almost-automorphisms
Every automorphism of
![]() $\mathcal {T}_d$
induces a self-homeomorphism of the boundary
$\mathcal {T}_d$
induces a self-homeomorphism of the boundary
![]() $\partial \mathcal {T}_d$
, which is a d-ary Cantor space. The idea behind almost-automorphisms of
$\partial \mathcal {T}_d$
, which is a d-ary Cantor space. The idea behind almost-automorphisms of
![]() $\mathcal {T}_d$
is to consider self-homeomorphisms of
$\mathcal {T}_d$
is to consider self-homeomorphisms of
![]() $\partial \mathcal {T}_d$
that locally “look like” they came from
$\partial \mathcal {T}_d$
that locally “look like” they came from
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Far more detail and rigor can be found, for example, in [Reference LeBoudecLB17] and [Reference SteinSZ21, Section 1.3]. For our purposes here, we will use the isomorphism in [Reference SteinSZ21, Theorem 2.6] to simply define the group of almost-automorphisms of
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. Far more detail and rigor can be found, for example, in [Reference LeBoudecLB17] and [Reference SteinSZ21, Section 1.3]. For our purposes here, we will use the isomorphism in [Reference SteinSZ21, Theorem 2.6] to simply define the group of almost-automorphisms of
![]() $\mathcal {T}_d$
as the Thompson-like group arising from the following cloning system.
$\mathcal {T}_d$
as the Thompson-like group arising from the following cloning system.
For
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
(in [Reference SteinSZ21], this was denoted
![]() $A_n$
, but here we will use
$A_n$
, but here we will use
![]() $W_n$
). Here, the wreath product has no subscript, and so this should be interpreted as meaning there are n copies of
$W_n$
). Here, the wreath product has no subscript, and so this should be interpreted as meaning there are n copies of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
and
$\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
and
![]() $S_n$
acts on
$S_n$
acts on
![]() $\{1,\dots ,n\}$
in the standard way. Following [Reference SteinSZ21, Section 2.2], we will define a d-ary cloning system on
$\{1,\dots ,n\}$
in the standard way. Following [Reference SteinSZ21, Section 2.2], we will define a d-ary cloning system on
![]() $(W_n)_{n\in \mathbb {N}}$
. Let
$(W_n)_{n\in \mathbb {N}}$
. Let
![]() $\rho _n \, {\colon}\, W_n \to S_n$
be the natural epimorphism onto the
$\rho _n \, {\colon}\, W_n \to S_n$
be the natural epimorphism onto the
![]() $S_n$
term, i.e.,
$S_n$
term, i.e.,
To define the d-ary cloning maps
![]() $\kappa _k^n \, {\colon}\, W_n \to W_{n+d-1}$
, we need some notation. Given
$\kappa _k^n \, {\colon}\, W_n \to W_{n+d-1}$
, we need some notation. Given
![]() $\sigma (f_1,\dots ,f_n)\in W_n$
and
$\sigma (f_1,\dots ,f_n)\in W_n$
and
![]() $1\le k\le n$
, write the wreath recursion of
$1\le k\le n$
, write the wreath recursion of
![]() $f_k$
as
$f_k$
as
![]() ${f_k=\rho (f_k)(f_k^1,\dots ,f_k^d)}$
. Also, write
${f_k=\rho (f_k)(f_k^1,\dots ,f_k^d)}$
. Also, write
![]() $\rho ^{(k)}(f_k)\in S_{n+d-1}$
for the image of
$\rho ^{(k)}(f_k)\in S_{n+d-1}$
for the image of
![]() $\rho (f_k)\in S_d$
under the (k-dependent) monomorphism
$\rho (f_k)\in S_d$
under the (k-dependent) monomorphism
![]() $S_d\to S_{n+d-1}$
induced by the inclusion
$S_d\to S_{n+d-1}$
induced by the inclusion
![]() $\{1,\dots ,d\}\to \{1,\dots ,n\}$
sending j to
$\{1,\dots ,d\}\to \{1,\dots ,n\}$
sending j to
![]() $k+j-1$
. Now we can define
$k+j-1$
. Now we can define
![]() $\kappa _k^n$
as follows:
$\kappa _k^n$
as follows:
As proved in [Reference SteinSZ21, Proposition 2.4], these
![]() $\rho _n$
and
$\rho _n$
and
![]() $\kappa _k^n$
define a d-ary cloning system on the
$\kappa _k^n$
define a d-ary cloning system on the
![]() $W_n$
.
$W_n$
.
Definition 3.3 (Group of almost-automorphisms)
The group of almost-automorphisms
![]() $\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
of
$\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
of
![]() $\mathcal {T}_d$
is
$\mathcal {T}_d$
is
where
![]() $(W_n)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
$(W_n)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
Now, for self-similar
![]() $G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, consider the family
$G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, consider the family
![]() $(S_n \wr G)_{n\in \mathbb {N}}$
. Thanks to self-similarity, the restriction of
$(S_n \wr G)_{n\in \mathbb {N}}$
. Thanks to self-similarity, the restriction of
![]() $\kappa _k^n$
to
$\kappa _k^n$
to
![]() $S_n \wr G$
lands in
$S_n \wr G$
lands in
![]() $S_{n+d-1} \wr G$
, which means that the d-ary cloning system on the
$S_{n+d-1} \wr G$
, which means that the d-ary cloning system on the
![]() $W_n=S_n \wr \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
restricts to a d-ary cloning system on
$W_n=S_n \wr \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
restricts to a d-ary cloning system on
![]() $S_n \wr G$
.
$S_n \wr G$
.
Definition 3.4 (Röver–Nekrashevych group)
For a self-similar group
![]() $G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the Röver–Nekrashevych group for G is
$G\le \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the Röver–Nekrashevych group for G is
where
![]() $(S_n\wr G)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
$(S_n\wr G)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
This definition agrees with the usual definition first given by Nekrashevych [Reference NekrashevychNek04], thanks to [Reference SteinSZ21, Corollary 2.7].
Definition 3.5 (Röver group)
The Röver group is the group
![]() $V_2(\operatorname {\mathrm {Grig}})$
.
$V_2(\operatorname {\mathrm {Grig}})$
.
The Röver group
![]() $V_2(\operatorname {\mathrm {Grig}})$
was first constructed by Röver in [Reference RöverRöv99], and generalized by Nekrashevych in [Reference NekrashevychNek04] to the full family of Röver–Nekrashevych groups
$V_2(\operatorname {\mathrm {Grig}})$
was first constructed by Röver in [Reference RöverRöv99], and generalized by Nekrashevych in [Reference NekrashevychNek04] to the full family of Röver–Nekrashevych groups
![]() $V_d(G)$
. Röver proved that
$V_d(G)$
. Röver proved that
![]() $V_2(\operatorname {\mathrm {Grig}})$
is isomorphic to the abstract commensurator of
$V_2(\operatorname {\mathrm {Grig}})$
is isomorphic to the abstract commensurator of
![]() $\operatorname {\mathrm {Grig}}$
, and is a finitely presented simple group [Reference RöverRöv02, Reference RöverRöv99]. Belk and Matucci [Reference Brady, Burillo, Cleary and SteinBM16] proved that it is even of type
$\operatorname {\mathrm {Grig}}$
, and is a finitely presented simple group [Reference RöverRöv02, Reference RöverRöv99]. Belk and Matucci [Reference Brady, Burillo, Cleary and SteinBM16] proved that it is even of type
![]() $\operatorname {\mathrm {F}}_\infty $
. Analogous results for certain
$\operatorname {\mathrm {F}}_\infty $
. Analogous results for certain
![]() $V_d(G)$
were proved by Nekrashevych [Reference NekrashevychNek04], Farley and Hughes [Reference Farley and HughesFH15], and the authors [Reference SteinSZ21].
$V_d(G)$
were proved by Nekrashevych [Reference NekrashevychNek04], Farley and Hughes [Reference Farley and HughesFH15], and the authors [Reference SteinSZ21].
3.3 Braiding groups of almost-automorphisms
Now we will introduce braided Röver–Nekrashevych groups. Starting with self-identical groups, this was previously done by Aroca and Cumplido in [Reference AllcockAC22], but for self-similar groups that are not self-identical, to the best of our knowledge, this has not been done. In particular, using the braided Grigorchuk group to construct a braided Röver group is new. As a remark, Aroca and Cumplido’s constructions could have been phrased in the language of cloning systems, as they mention in their introduction (though they did not use this framework outside their introduction), so one can view our approach here as a direct generalization of theirs.
Convention: The notation
![]() $B_n \wr G$
, i.e., with no subscript on the
$B_n \wr G$
, i.e., with no subscript on the
![]() $\wr $
, will always mean
$\wr $
, will always mean
![]() $B_n \wr _{\{1,\dots ,n\}} G$
defined via the action of the braid group
$B_n \wr _{\{1,\dots ,n\}} G$
defined via the action of the braid group
![]() $B_n$
on
$B_n$
on
![]() $\{1,\dots ,n\}$
coming from the natural projection
$\{1,\dots ,n\}$
coming from the natural projection
![]() $B_n \to S_n$
.
$B_n \to S_n$
.
Recall that
![]() $\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)=B_d \wr _X^\infty B_d$
, and let
$\operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)=B_d \wr _X^\infty B_d$
, and let
. We want to define a d-ary cloning system on
![]() $(\operatorname {br}\!W_n)_{n\in \mathbb {N}}$
. We will use the notation
$(\operatorname {br}\!W_n)_{n\in \mathbb {N}}$
. We will use the notation
![]() $\rho _n$
and
$\rho _n$
and
![]() $\kappa _k^n$
like we did in the nonbraided case for the cloning system on
$\kappa _k^n$
like we did in the nonbraided case for the cloning system on
![]() $(W_n)_{n\in \mathbb {N}}$
, and no confusion should arise. Let
$(W_n)_{n\in \mathbb {N}}$
, and no confusion should arise. Let
![]() $\rho _n\, {\colon}\, \operatorname{br}\!W_n \to S_n$
be the composition of
$\rho _n\, {\colon}\, \operatorname{br}\!W_n \to S_n$
be the composition of
![]() $\operatorname {br}\!W_n \to W_n$
with
$\operatorname {br}\!W_n \to W_n$
with
![]() $W_n \to S_n$
, where the first map is induced by the standard epimorphism
$W_n \to S_n$
, where the first map is induced by the standard epimorphism
![]() $B_n\to S_n$
together with
$B_n\to S_n$
together with
![]() $\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, and the second map is the
$\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, and the second map is the
![]() $\rho _n$
epimorphism from the nonbraided case. To define the d-ary cloning maps
$\rho _n$
epimorphism from the nonbraided case. To define the d-ary cloning maps
![]() $\kappa _k^n \, {\colon}\, \operatorname{br}\!W_n \to \operatorname {br}\!W_{n+d-1}$
, we need some notation. Given
$\kappa _k^n \, {\colon}\, \operatorname{br}\!W_n \to \operatorname {br}\!W_{n+d-1}$
, we need some notation. Given
![]() $\beta (f_1,\dots ,f_n)\in \operatorname {br}\!W_n$
and
$\beta (f_1,\dots ,f_n)\in \operatorname {br}\!W_n$
and
![]() $1\le k\le n$
, write the braided wreath recursion of
$1\le k\le n$
, write the braided wreath recursion of
![]() $f_k$
as
$f_k$
as
![]() $f_k=\phi (f_k)(f_k^1,\dots ,f_k^d)$
. Also, write
$f_k=\phi (f_k)(f_k^1,\dots ,f_k^d)$
. Also, write
![]() $\phi ^{(k)}(f_k)\in B_{n+d-1}$
for the image of
$\phi ^{(k)}(f_k)\in B_{n+d-1}$
for the image of
![]() $\phi (f_k)\in B_d$
under the (k-dependent) monomorphism
$\phi (f_k)\in B_d$
under the (k-dependent) monomorphism
![]() $B_d\to B_{n+d-1}$
induced by adding
$B_d\to B_{n+d-1}$
induced by adding
![]() $k-1$
new unbraided strands on the left and
$k-1$
new unbraided strands on the left and
![]() $n-k$
new unbraided strands on the right. Now we can define
$n-k$
new unbraided strands on the right. Now we can define
![]() $\kappa _k^n$
as follows:
$\kappa _k^n$
as follows:
Note that
![]() $\kappa _k^n$
is injective, since
$\kappa _k^n$
is injective, since
![]() $\vartheta _k^n$
is injective and
$\vartheta _k^n$
is injective and
![]() $f_k$
is uniquely determined by its braided wreath recursion. See Figure 2 for example.
$f_k$
is uniquely determined by its braided wreath recursion. See Figure 2 for example.
Proposition 3.4
![]() $((\operatorname {br}\!W_n)_{n\in \mathbb {N}},(\rho _n)_{n\in \mathbb {N}},(\kappa _k^n)_{1\le k\le n})$
is a d-ary cloning system.
$((\operatorname {br}\!W_n)_{n\in \mathbb {N}},(\rho _n)_{n\in \mathbb {N}},(\kappa _k^n)_{1\le k\le n})$
is a d-ary cloning system.
Proof The proof is similar to that of [Reference SteinSZ21, Proposition 2.4] about the nonbraided situation, and some parts work in exactly the same way. Hence, in the course of this proof, we will sometimes just state that a certain step works analogously to the corresponding step in [Reference SteinSZ21, Proposition 2.4]. First, we prove (C1) (cloning a product). Let
![]() $f=\beta (f_1,\dots ,f_n)$
and
$f=\beta (f_1,\dots ,f_n)$
and
![]() $g=\gamma (g_1,\dots ,g_n)$
be elements of
$g=\gamma (g_1,\dots ,g_n)$
be elements of
![]() $\operatorname {br}\!W_n$
, so the product
$\operatorname {br}\!W_n$
, so the product
![]() $fg$
equals
$fg$
equals
![]() $\beta \gamma (f_{\gamma (1)}g_1,\dots ,f_{\gamma (n)}g_n)$
. Here,
$\beta \gamma (f_{\gamma (1)}g_1,\dots ,f_{\gamma (n)}g_n)$
. Here,
![]() $B_n$
acts on
$B_n$
acts on
![]() $\{1,\dots ,n\}$
via the projection
$\{1,\dots ,n\}$
via the projection
![]() $B_n\to S_n$
, and the notation
$B_n\to S_n$
, and the notation
![]() $\gamma (i)$
indicates this action. Similar to the proof of [Reference SteinSZ21, Proposition 2.4], the left-hand side of (C1) is
$\gamma (i)$
indicates this action. Similar to the proof of [Reference SteinSZ21, Proposition 2.4], the left-hand side of (C1) is
 $$ \begin{align*} &(fg)\kappa_k^n = (\beta\gamma)\vartheta_k^n \phi^{(k)}(f_{\gamma(k)}g_k)\\ &\quad\times (f_{\gamma(1)}g_1,\dots,f_{\gamma(k-1)}g_{k-1},f_{\gamma(k)}^{\phi(g_k)(1)}g_k^1,\dots,f_{\gamma(k)}^{\phi(g_k)(d)}g_k^d,f_{\gamma(k+1)}g_{k+1},\dots,f_{\gamma(n)}g_n) \text{.} \end{align*} $$
$$ \begin{align*} &(fg)\kappa_k^n = (\beta\gamma)\vartheta_k^n \phi^{(k)}(f_{\gamma(k)}g_k)\\ &\quad\times (f_{\gamma(1)}g_1,\dots,f_{\gamma(k-1)}g_{k-1},f_{\gamma(k)}^{\phi(g_k)(1)}g_k^1,\dots,f_{\gamma(k)}^{\phi(g_k)(d)}g_k^d,f_{\gamma(k+1)}g_{k+1},\dots,f_{\gamma(n)}g_n) \text{.} \end{align*} $$
Here, the braided wreath recursions of
![]() $f_{\gamma (k)}$
and
$f_{\gamma (k)}$
and
![]() $g_k$
are
$g_k$
are
![]() $f_{\gamma (k)}=\phi (f_{\gamma (k)})(f_{\gamma (k)}^1,\dots ,f_{\gamma (k)}^d)$
and
$f_{\gamma (k)}=\phi (f_{\gamma (k)})(f_{\gamma (k)}^1,\dots ,f_{\gamma (k)}^d)$
and
![]() $g_k=\phi (g_k)(g_k^1,\dots ,g_k^d)$
, so the braided wreath recursion of
$g_k=\phi (g_k)(g_k^1,\dots ,g_k^d)$
, so the braided wreath recursion of
![]() $f_{\gamma (k)}g_k$
is
$f_{\gamma (k)}g_k$
is
Now we need to show that the right-hand side of (C1), which is
![]() $(f)\kappa _{\gamma (k)}^n(g)\kappa _k^n$
, equals the same thing. One can compute (similar to the proof of [Reference SteinSZ21, Proposition 2.4]) that this equals
$(f)\kappa _{\gamma (k)}^n(g)\kappa _k^n$
, equals the same thing. One can compute (similar to the proof of [Reference SteinSZ21, Proposition 2.4]) that this equals
 $$ \begin{align*} &(\beta)\vartheta_{\gamma(k)}^n \phi^{(\gamma(k))}(f_{\gamma(k)}) (\gamma)\vartheta_k^n \phi^{(k)}(g_k) \\ &\times (f_1,\dots,f_{\gamma(k)-1},f_{\gamma(k)}^1,\dots,f_{\gamma(k)}^d,f_{\gamma(k)+1},\dots,f_n)^{(\gamma)\vartheta_k^n \phi^{(k)}(g_k)} \\ &\times (g_1,\dots,g_{k-1},g_k^1,\dots,g_k^d,g_{k+1},\dots,g_n) \text{,} \end{align*} $$
$$ \begin{align*} &(\beta)\vartheta_{\gamma(k)}^n \phi^{(\gamma(k))}(f_{\gamma(k)}) (\gamma)\vartheta_k^n \phi^{(k)}(g_k) \\ &\times (f_1,\dots,f_{\gamma(k)-1},f_{\gamma(k)}^1,\dots,f_{\gamma(k)}^d,f_{\gamma(k)+1},\dots,f_n)^{(\gamma)\vartheta_k^n \phi^{(k)}(g_k)} \\ &\times (g_1,\dots,g_{k-1},g_k^1,\dots,g_k^d,g_{k+1},\dots,g_n) \text{,} \end{align*} $$
where the superscript indicates conjugation in
![]() $\operatorname {br}\!W_{n+d-1}$
. By the same argument as in the proof of [Reference SteinSZ21, Proposition 2.4], the “tuple parts” of the left- and right-hand sides of (C1) are the same, so we only need to show that the “braid parts” are the same, i.e., that
$\operatorname {br}\!W_{n+d-1}$
. By the same argument as in the proof of [Reference SteinSZ21, Proposition 2.4], the “tuple parts” of the left- and right-hand sides of (C1) are the same, so we only need to show that the “braid parts” are the same, i.e., that
![]() $(\beta \gamma )\vartheta _k^n \phi ^{(k)}(f_{\gamma (k)}g_k) = (\beta )\vartheta _{\gamma (k)}^n \phi ^{(\gamma (k))}(f_{\gamma (k)}) (\gamma )\vartheta _k^n \phi ^{(k)}(g_k)$
. Since we already know the
$(\beta \gamma )\vartheta _k^n \phi ^{(k)}(f_{\gamma (k)}g_k) = (\beta )\vartheta _{\gamma (k)}^n \phi ^{(\gamma (k))}(f_{\gamma (k)}) (\gamma )\vartheta _k^n \phi ^{(k)}(g_k)$
. Since we already know the
![]() $\vartheta _k^n$
define a d-ary cloning system on braid groups, we know
$\vartheta _k^n$
define a d-ary cloning system on braid groups, we know
![]() $(\beta \gamma )\vartheta _k^n=(\beta )\vartheta _{\gamma (k)}^n(\gamma )\vartheta _k^n$
, and since
$(\beta \gamma )\vartheta _k^n=(\beta )\vartheta _{\gamma (k)}^n(\gamma )\vartheta _k^n$
, and since
![]() $\phi $
is a homomorphism, this means that it suffices to show that
$\phi $
is a homomorphism, this means that it suffices to show that
![]() $(\gamma )\vartheta _k^n \phi ^{(k)}(f_{\gamma (k)}) = \phi ^{(\gamma (k))}(f_{\gamma (k)}) (\gamma )\vartheta _k^n$
. To see this, note that the kth to
$(\gamma )\vartheta _k^n \phi ^{(k)}(f_{\gamma (k)}) = \phi ^{(\gamma (k))}(f_{\gamma (k)}) (\gamma )\vartheta _k^n$
. To see this, note that the kth to
![]() $(k+d-1)$
st strands of
$(k+d-1)$
st strands of
![]() $(\gamma )\vartheta _k^n$
are all parallel to each other, and these are the only strands of
$(\gamma )\vartheta _k^n$
are all parallel to each other, and these are the only strands of
![]() $\phi ^{(k)}(f_{\gamma (k)})$
that can braid nontrivially (see Figure 3).
$\phi ^{(k)}(f_{\gamma (k)})$
that can braid nontrivially (see Figure 3).

Figure 3: An example of the last step of the verification of (C1) in the proof of Proposition 3.4. Here,
![]() $d=3$
,
$d=3$
,
![]() $k=3$
, and
$k=3$
, and
![]() $n=5$
.
$n=5$
.
Next, (C2) follows by an exactly analogous argument to the proof of [Reference SteinSZ21, Proposition 2.4].
Finally, we turn to (C3). Let
![]() $\beta (f_1,\dots ,f_n)\in \operatorname {br}\!W_n$
and
$\beta (f_1,\dots ,f_n)\in \operatorname {br}\!W_n$
and
![]() $i\ne k,k+1,\dots ,k+d-1$
. We need to show that
$i\ne k,k+1,\dots ,k+d-1$
. We need to show that
![]() $\rho _{n+d-1}((\beta (f_1,\dots ,f_n))\kappa _k^n)(i) = (\rho _n(\beta (f_1,\dots ,f_n)))\varsigma _k^n(i)$
. Setting
$\rho _{n+d-1}((\beta (f_1,\dots ,f_n))\kappa _k^n)(i) = (\rho _n(\beta (f_1,\dots ,f_n)))\varsigma _k^n(i)$
. Setting
![]() $\sigma =\pi (\beta )$
, the right-hand side just equals
$\sigma =\pi (\beta )$
, the right-hand side just equals
![]() $(\sigma )\varsigma _k^n(i)$
. The left-hand side equals
$(\sigma )\varsigma _k^n(i)$
. The left-hand side equals
which is
![]() $\pi ((\beta )\vartheta _k^n\phi ^{(k)}(f_k))(i)$
. Since
$\pi ((\beta )\vartheta _k^n\phi ^{(k)}(f_k))(i)$
. Since
![]() $\pi (\phi ^{(k)}(f_k))(i)=i$
(by virtue of
$\pi (\phi ^{(k)}(f_k))(i)=i$
(by virtue of
![]() $i\ne k,k+1,\dots ,k+d-1$
), this equals
$i\ne k,k+1,\dots ,k+d-1$
), this equals
![]() $\pi ((\beta )\vartheta _k^n)(i)$
. Since
$\pi ((\beta )\vartheta _k^n)(i)$
. Since
![]() $\pi $
plays the role of
$\pi $
plays the role of
![]() $\rho _n$
in the d-ary cloning system on the braid groups using the d-ary cloning maps
$\rho _n$
in the d-ary cloning system on the braid groups using the d-ary cloning maps
![]() $\vartheta _k^n$
, by (C3) for that d-ary cloning system, we know
$\vartheta _k^n$
, by (C3) for that d-ary cloning system, we know
![]() $\pi ((\beta )\vartheta _k^n)(i) = (\sigma )\varsigma _k^n(i)$
as desired.
$\pi ((\beta )\vartheta _k^n)(i) = (\sigma )\varsigma _k^n(i)$
as desired.
The Thompson-like group
![]() $\mathscr {T}_d(\operatorname {br}\!W_*)$
is a braided version of
$\mathscr {T}_d(\operatorname {br}\!W_*)$
is a braided version of
![]() $\mathscr {T}_d(W_*)=\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
, and we will denote it by
$\mathscr {T}_d(W_*)=\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
, and we will denote it by
![]() $\operatorname {br}\!\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
.
$\operatorname {br}\!\operatorname {\mathrm {AAut}}(\mathcal {T}_d)$
.
Now, for braided self-similar
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, consider the family
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, consider the family
![]() $(B_n \wr G)_{n\in \mathbb {N}}$
. Thanks to braided self-similarity, the restriction of
$(B_n \wr G)_{n\in \mathbb {N}}$
. Thanks to braided self-similarity, the restriction of
![]() $\kappa _k^n$
to
$\kappa _k^n$
to
![]() $B_n \wr G$
lands in
$B_n \wr G$
lands in
![]() $B_{n+d-1} \wr G$
, which means that the d-ary cloning system on the
$B_{n+d-1} \wr G$
, which means that the d-ary cloning system on the
![]() $\operatorname {br}\!W_n=B_n \wr \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
restricts to a d-ary cloning system on the
$\operatorname {br}\!W_n=B_n \wr \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
restricts to a d-ary cloning system on the
![]() $B_n \wr G$
.
$B_n \wr G$
.
Definition 3.6 (Braided Röver–Nekrashevych group)
For a braided self-similar group
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the braided Röver–Nekrashevych group for G is
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
, the braided Röver–Nekrashevych group for G is
where
![]() $(B_n\wr G)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
$(B_n\wr G)_{n\in \mathbb {N}}$
is equipped with the above d-ary cloning system.
Our main example is the following.
Definition 3.7 (Braided Röver group)
We define the braided Röver group to be the group
![]() $\operatorname {br}\!V_2(\operatorname {\mathrm {brGrig}})$
.
$\operatorname {br}\!V_2(\operatorname {\mathrm {brGrig}})$
.
See Figure 4 for an example of an element of the braided Röver group.

Figure 4: An element of the braided Röver group. Here, we draw a triple
![]() $(T_-,\beta (f_1,\dots ,f_m),T_+)$
with
$(T_-,\beta (f_1,\dots ,f_m),T_+)$
with
![]() $T_+$
upside down so that
$T_+$
upside down so that
![]() $\beta $
is a braid from the leaves of
$\beta $
is a braid from the leaves of
![]() $T_-$
to the leaves of
$T_-$
to the leaves of
![]() $T_+$
, and the
$T_+$
, and the
![]() $f_i$
label the strands. The element equals
$f_i$
label the strands. The element equals
![]() $[\wedge ,(a,b),\wedge ]$
, for
$[\wedge ,(a,b),\wedge ]$
, for
![]() $\wedge $
the tree with one caret. As indicated in the picture, after expansions, this is the same element as
$\wedge $
the tree with one caret. As indicated in the picture, after expansions, this is the same element as
![]() $[T,\beta (1,1,a,c),T]$
for T the result of adding a caret to each leaf of
$[T,\beta (1,1,a,c),T]$
for T the result of adding a caret to each leaf of
![]() $\wedge $
and
$\wedge $
and
![]() $\beta \in B_4$
the braid crossing the first strand over the second.
$\beta \in B_4$
the braid crossing the first strand over the second.
There is an obvious relationship between braided Röver–Nekrashevych groups and (nonbraided) Röver–Nekrashevych groups, analogous to how the braided Thompson group
![]() $\operatorname {br}\!V$
surjects onto Thompson’s group V. Given a braided Röver–Nekrashevych group
$\operatorname {br}\!V$
surjects onto Thompson’s group V. Given a braided Röver–Nekrashevych group
![]() $\operatorname {br}\!V_d(G)$
, we get a well-defined epimorphism
$\operatorname {br}\!V_d(G)$
, we get a well-defined epimorphism
where
![]() $\pi (G)$
is the image of G under
$\pi (G)$
is the image of G under
![]() $\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d) \to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. This epimorphism (which by abuse of notation we are also denoting by
$\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d) \to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. This epimorphism (which by abuse of notation we are also denoting by
![]() $\pi $
) is given by sending
$\pi $
) is given by sending
![]() $[T_-,\beta (f_1,\dots ,f_n),T_+]$
to
$[T_-,\beta (f_1,\dots ,f_n),T_+]$
to
![]() $[T_-,\pi (\beta )(\pi (f_1),\dots ,\pi (f_n)),T_+]$
. The d-ary cloning systems on
$[T_-,\pi (\beta )(\pi (f_1),\dots ,\pi (f_n)),T_+]$
. The d-ary cloning systems on
![]() $(B_n\wr G)_{n\in \mathbb {N}}$
and
$(B_n\wr G)_{n\in \mathbb {N}}$
and
![]() $(S_n\wr \pi (G))_{n\in \mathbb {N}}$
are clearly respected by
$(S_n\wr \pi (G))_{n\in \mathbb {N}}$
are clearly respected by
![]() $\pi $
, so this map really is well defined.
$\pi $
, so this map really is well defined.
Remark 3.5 The kernel of
![]() $\pi \, {\colon}\, \operatorname{br}\!V_d(G)\to V_d(\pi (G))$
consists of all
$\pi \, {\colon}\, \operatorname{br}\!V_d(G)\to V_d(\pi (G))$
consists of all
![]() $[T,\beta (f_1,\dots ,f_n),T]$
such that
$[T,\beta (f_1,\dots ,f_n),T]$
such that
![]() $\beta $
is pure and each
$\beta $
is pure and each
![]() $f_i$
lies in the kernel of
$f_i$
lies in the kernel of
![]() $\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. By Lemma 2.6, each of these kernels is a direct product of copies of
$\pi \, {\colon}\, \operatorname{br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)\to \operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
. By Lemma 2.6, each of these kernels is a direct product of copies of
![]() $PB_d$
. Overall, this means that the kernel of
$PB_d$
. Overall, this means that the kernel of
![]() $\pi \, {\colon}\, \operatorname{br}\!V_d(G)\to V_d(\pi (G))$
is a direct limit of direct products of pure braid groups
$\pi \, {\colon}\, \operatorname{br}\!V_d(G)\to V_d(\pi (G))$
is a direct limit of direct products of pure braid groups
![]() $PB_n$
with infinitely many copies of
$PB_n$
with infinitely many copies of
![]() $PB_d$
, with the direct limit informed by the cloning maps.
$PB_d$
, with the direct limit informed by the cloning maps.
4 Finiteness properties
In this section, we inspect finiteness properties of braided Röver–Nekrashevych groups. The main result of this section is the following theorem.
Theorem 4.1 Let
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
be braided self-similar. If G is of type
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
be braided self-similar. If G is of type
![]() $\operatorname {\mathrm {F}}_n$
, then so is
$\operatorname {\mathrm {F}}_n$
, then so is
![]() $\operatorname {br}\!V_d(G)$
.
$\operatorname {br}\!V_d(G)$
.
The case when G is braided self-identical was already proved in [Reference Skipper and ZaremskySW], where it was shown that for braided self-identical G, the converse of Theorem 4.1 is also true. (In general, the converse of Theorem 4.1 is not always true, as our Theorem 5.1 will show.)
4.1 Stein–Farley complexes
The starting point for deducing finiteness properties for a Thompson-like group is often to construct a so-called Stein–Farley complex on which the group can act. For groups of the form
![]() $\mathscr {T}_2(G_*)$
, i.e., those arising from (
$\mathscr {T}_2(G_*)$
, i.e., those arising from (
![]() $2$
-ary) cloning systems, this was done in [Reference Witzel and ZaremskyWZ18]. For groups of the form
$2$
-ary) cloning systems, this was done in [Reference Witzel and ZaremskyWZ18]. For groups of the form
![]() $\mathscr {T}_d(S_*\wr G)$
, i.e., Röver–Nekrashevych groups, the Stein–Farley construction was done in [Reference SteinSZ21]. For arbitrary groups of the form
$\mathscr {T}_d(S_*\wr G)$
, i.e., Röver–Nekrashevych groups, the Stein–Farley construction was done in [Reference SteinSZ21]. For arbitrary groups of the form
![]() $\mathscr {T}_d(G_*)$
, i.e., those arising from d-ary cloning systems in general, the Stein–Farley construction has not technically been done in the literature, but it is easy to mimic the
$\mathscr {T}_d(G_*)$
, i.e., those arising from d-ary cloning systems in general, the Stein–Farley construction has not technically been done in the literature, but it is easy to mimic the
![]() $2$
-ary construction, and this is the goal of this subsection. Also, see [Reference ZaremskyZar21] for an introductory take on the situation when
$2$
-ary construction, and this is the goal of this subsection. Also, see [Reference ZaremskyZar21] for an introductory take on the situation when
![]() $d=2$
and
$d=2$
and
![]() $G_m=\{1\}$
for all m, i.e., for Thompson’s group F. The name Stein–Farley complex pays homage to Stein [Reference Skipper and WuSte92] and Farley [Reference FarleyFar03], who constructed complexes like these for the classical Thompson groups and some close relatives.
$G_m=\{1\}$
for all m, i.e., for Thompson’s group F. The name Stein–Farley complex pays homage to Stein [Reference Skipper and WuSte92] and Farley [Reference FarleyFar03], who constructed complexes like these for the classical Thompson groups and some close relatives.
Given a d-ary cloning system
![]() $((G_m)_{m\in \mathbb {N}},(\rho _m)_{m\in \mathbb {N}},(\kappa _k^m)_{k\le m})$
, we will construct a cube complex, denoted by
$((G_m)_{m\in \mathbb {N}},(\rho _m)_{m\in \mathbb {N}},(\kappa _k^m)_{k\le m})$
, we will construct a cube complex, denoted by
![]() $\mathscr {X}_d(G_*)$
, called the Stein–Farley complex for the d-ary cloning system. This is done in a number of steps.
$\mathscr {X}_d(G_*)$
, called the Stein–Farley complex for the d-ary cloning system. This is done in a number of steps.
A groupoid: First, we consider the set of equivalence classes
![]() $[F_-,g,F_+]$
, where
$[F_-,g,F_+]$
, where
![]() $F_-$
is a d-ary forest, say with m leaves (and some number of roots), g is an element of
$F_-$
is a d-ary forest, say with m leaves (and some number of roots), g is an element of
![]() $G_m$
, and
$G_m$
, and
![]() $F_+$
is a d-ary forest with m leaves (and some number of roots). The equivalence relation on such triples is given by the expansion and reduction moves, as with elements of
$F_+$
is a d-ary forest with m leaves (and some number of roots). The equivalence relation on such triples is given by the expansion and reduction moves, as with elements of
![]() $\mathscr {T}_d(G_*)$
. This set is a groupoid; two elements
$\mathscr {T}_d(G_*)$
. This set is a groupoid; two elements
![]() $[F_-,g,F_+]$
and
$[F_-,g,F_+]$
and
![]() $[E_-,h,E_+]$
can be multiplied whenever the number of roots of
$[E_-,h,E_+]$
can be multiplied whenever the number of roots of
![]() $F_+$
equals the number of roots of
$F_+$
equals the number of roots of
![]() $E_-$
. In this case, up to expansions, we can assume that
$E_-$
. In this case, up to expansions, we can assume that
![]() $F_+=E_-$
, and the multiplication in this groupoid works analogously to the multiplication in
$F_+=E_-$
, and the multiplication in this groupoid works analogously to the multiplication in
![]() $\mathscr {T}_d(G_*)$
. Multiplication is well defined in the groupoid for all the same reasons that it is well defined in
$\mathscr {T}_d(G_*)$
. Multiplication is well defined in the groupoid for all the same reasons that it is well defined in
![]() $\mathscr {T}_d(G_*)$
. Denote this groupoid by
$\mathscr {T}_d(G_*)$
. Denote this groupoid by
![]() $\mathscr {G}_d(G_*)$
.
$\mathscr {G}_d(G_*)$
.
A poset: Now we restrict to equivalence classes of triples of the form
![]() $[T_-,g,F_+]$
for
$[T_-,g,F_+]$
for
![]() $T_-$
a d-ary tree, and mod out an additional equivalence relation given by right multiplication by elements of the form
$T_-$
a d-ary tree, and mod out an additional equivalence relation given by right multiplication by elements of the form
![]() $[1,g',1]$
, for
$[1,g',1]$
, for
![]() $1$
a trivial forest with some number of roots, m, and
$1$
a trivial forest with some number of roots, m, and
![]() $g'\in G_m$
. Denote the resulting equivalence classes by
$g'\in G_m$
. Denote the resulting equivalence classes by
![]() $[T_-,g,F_+]_G$
, and write
$[T_-,g,F_+]_G$
, and write
![]() $\mathscr {P}_d(G_*)$
for the set of all of them. Given
$\mathscr {P}_d(G_*)$
for the set of all of them. Given
![]() $[T_-,g,F_+]_G\in \mathscr {P}_d(G_*)$
, say with
$[T_-,g,F_+]_G\in \mathscr {P}_d(G_*)$
, say with
![]() $F_+$
having m roots, and a groupoid element of the form
$F_+$
having m roots, and a groupoid element of the form
![]() $[F,1,1]$
for F a d-ary forest with m roots, it makes sense to consider the product
$[F,1,1]$
for F a d-ary forest with m roots, it makes sense to consider the product
![]() $[T_-,g,F_+][F,1,1]$
and the equivalence class
$[T_-,g,F_+][F,1,1]$
and the equivalence class
![]() $[T_-,g,F_+][F,1,1]_G$
. We define a partial order
$[T_-,g,F_+][F,1,1]_G$
. We define a partial order
![]() $\le $
on
$\le $
on
![]() $\mathscr {P}_d(G_*)$
by declaring
$\mathscr {P}_d(G_*)$
by declaring
(Note that thanks to the equivalence relation, in fact, we have
for any relevant
![]() $g'$
.) It is easy to see that
$g'$
.) It is easy to see that
![]() $\le $
is reflexive, transitive, and antisymmetric, and hence really is a partial order. It is also clear that
$\le $
is reflexive, transitive, and antisymmetric, and hence really is a partial order. It is also clear that
![]() $\mathscr {P}_d(G_*)$
with
$\mathscr {P}_d(G_*)$
with
![]() $\le $
is a directed poset, since for any
$\le $
is a directed poset, since for any
![]() $[T_-,g,F_+]_G$
we have
$[T_-,g,F_+]_G$
we have
![]() $[T_-,g,F_+]_G \le [T_-,g,1]_G=[T_-,1,1]_G$
, and any two
$[T_-,g,F_+]_G \le [T_-,g,1]_G=[T_-,1,1]_G$
, and any two
![]() $[T_-,1,1]_G$
and
$[T_-,1,1]_G$
and
![]() $[T_-',1,1]_G$
have an upper bound. Hence, the geometric realization
$[T_-',1,1]_G$
have an upper bound. Hence, the geometric realization
![]() $|\mathscr {P}_d(G_*)|$
is contractible.
$|\mathscr {P}_d(G_*)|$
is contractible.
A cube complex: Now we construct the Stein–Farley complex
![]() $\mathscr {X}_d(G_*)$
, which is a cube complex having a natural subdivision identifiable with a certain subcomplex of
$\mathscr {X}_d(G_*)$
, which is a cube complex having a natural subdivision identifiable with a certain subcomplex of
![]() $|\mathscr {P}_d(G_*)|$
. The vertex set of
$|\mathscr {P}_d(G_*)|$
. The vertex set of
![]() $\mathscr {X}_d(G_*)$
is the whole vertex set of
$\mathscr {X}_d(G_*)$
is the whole vertex set of
![]() $|\mathscr {P}_d(G_*)|$
, namely
$|\mathscr {P}_d(G_*)|$
, namely
![]() $\mathscr {P}_d(G_*)$
. Let E be a d-ary forest whose trees each have at most one d-caret; call such a d-ary forest elementary. If E is an elementary d-ary forest with one nontrivial tree and with the same number of roots as
$\mathscr {P}_d(G_*)$
. Let E be a d-ary forest whose trees each have at most one d-caret; call such a d-ary forest elementary. If E is an elementary d-ary forest with one nontrivial tree and with the same number of roots as
![]() $F_+$
, we can consider the product
$F_+$
, we can consider the product
![]() $[T_-,g,F_+][E,1,1]$
in the groupoid
$[T_-,g,F_+][E,1,1]$
in the groupoid
![]() $\mathscr {G}_d(G_*)$
. We declare that the vertices
$\mathscr {G}_d(G_*)$
. We declare that the vertices
![]() $[T_-,g,F_+]_G$
and
$[T_-,g,F_+]_G$
and
![]() $[T_-,g,F_+][E,1,1]_G$
span an edge in
$[T_-,g,F_+][E,1,1]_G$
span an edge in
![]() $\mathscr {X}_d(G_*)$
. If
$\mathscr {X}_d(G_*)$
. If
![]() $[T_-,g,F_+]_G\le [T_-,g,F_+][E,1,1]_G$
for E elementary, write
$[T_-,g,F_+]_G\le [T_-,g,F_+][E,1,1]_G$
for E elementary, write
More generally, if E is any elementary d-ary forest with the same number of roots as
![]() $F_+$
, then all the vertices of the form
$F_+$
, then all the vertices of the form
![]() $[T_-,g,F_+][E',1,1]_G$
, for
$[T_-,g,F_+][E',1,1]_G$
, for
![]() $E'$
obtained from E by replacing some number of d-carets with trivial trees, span the
$E'$
obtained from E by replacing some number of d-carets with trivial trees, span the
![]() $1$
-skeleton of a cube in
$1$
-skeleton of a cube in
![]() $\mathscr {X}_d(G_*)$
, and we declare that there is a cube in
$\mathscr {X}_d(G_*)$
, and we declare that there is a cube in
![]() $\mathscr {X}_d(G_*)$
with this
$\mathscr {X}_d(G_*)$
with this
![]() $1$
-skeleton. All of this is well defined up to the equivalence relation. Any nonempty intersection of cubes is a common face of each of them, so
$1$
-skeleton. All of this is well defined up to the equivalence relation. Any nonempty intersection of cubes is a common face of each of them, so
![]() $\mathscr {X}_d(G_*)$
really is a cube complex. Within a given cube, the geometric realization of the finite subposet of
$\mathscr {X}_d(G_*)$
really is a cube complex. Within a given cube, the geometric realization of the finite subposet of
![]() $\mathscr {P}_d(G_*)$
given by the vertices of the cube is naturally a subdivision of the cube. Hence, there is a natural subdivision of
$\mathscr {P}_d(G_*)$
given by the vertices of the cube is naturally a subdivision of the cube. Hence, there is a natural subdivision of
![]() $\mathscr {X}_d(G_*)$
that is identifiable with a subcomplex of
$\mathscr {X}_d(G_*)$
that is identifiable with a subcomplex of
![]() $|\mathscr {P}_d(G_*)|$
.
$|\mathscr {P}_d(G_*)|$
.
A Morse function: Let
be the function sending
![]() $[T_-,g,F_+]_G$
to the number of roots of
$[T_-,g,F_+]_G$
to the number of roots of
![]() $F_+$
, and call this the number of feet of this vertex. Note that adjacent vertices have distinct h values. By the construction of
$F_+$
, and call this the number of feet of this vertex. Note that adjacent vertices have distinct h values. By the construction of
![]() $\mathscr {X}_d(G_*)$
, it is clear that h can be extended to a map
$\mathscr {X}_d(G_*)$
, it is clear that h can be extended to a map
![]() $h\, {\colon}\, \mathscr {X}_d(G_*)\to \mathbb {R}$
that restricts to an affine map on each cube. Hence, h satisfies all the requirements to be a discrete Morse function, in the sense of Bestvina of Brady [Reference Bashwinger and ZaremskyBB97]. In particular, we will be allowed to use discrete Morse theory when it comes up later. The function h also comes into play when proving that
$h\, {\colon}\, \mathscr {X}_d(G_*)\to \mathbb {R}$
that restricts to an affine map on each cube. Hence, h satisfies all the requirements to be a discrete Morse function, in the sense of Bestvina of Brady [Reference Bashwinger and ZaremskyBB97]. In particular, we will be allowed to use discrete Morse theory when it comes up later. The function h also comes into play when proving that
![]() $\mathscr {X}_d(G_*)$
is contractible, which we do shortly.
$\mathscr {X}_d(G_*)$
is contractible, which we do shortly.
Upward-local finiteness: The main advantage of
![]() $\mathscr {X}_d(G_*)$
over
$\mathscr {X}_d(G_*)$
over
![]() $|\mathscr {P}_d(G_*)|$
is that the former is what we will call “upward-locally finite,” as we now explain. Note that there are only finitely many elementary d-ary forests with a given number of roots. Also, note that for any
$|\mathscr {P}_d(G_*)|$
is that the former is what we will call “upward-locally finite,” as we now explain. Note that there are only finitely many elementary d-ary forests with a given number of roots. Also, note that for any
![]() $[1,g,1],[F,1,1]\in \mathscr {G}_d(G_*)$
such that the product
$[1,g,1],[F,1,1]\in \mathscr {G}_d(G_*)$
such that the product
![]() $[1,g,1][F,1,1]$
makes sense, there exist
$[1,g,1][F,1,1]$
makes sense, there exist
![]() $F'$
and
$F'$
and
![]() $g'$
such that
$g'$
such that
![]() $[1,g,1][F,1,1]=[F',1,1][1,g',1]$
. More precisely,
$[1,g,1][F,1,1]=[F',1,1][1,g',1]$
. More precisely,
![]() $F'$
and
$F'$
and
![]() $g'$
are such that upon expanding we get
$g'$
are such that upon expanding we get
![]() $[1,g,1]=[F',g',F]$
, and then
$[1,g,1]=[F',g',F]$
, and then
In particular, given any vertex
![]() $x=[T_-,g,F_+]_G$
of
$x=[T_-,g,F_+]_G$
of
![]() $\mathscr {X}_d(G_*)$
, every vertex y with
$\mathscr {X}_d(G_*)$
, every vertex y with
![]() $x\preceq y$
is of the form
$x\preceq y$
is of the form
![]() $y=[T_-,g,F_+][E,1,1]_G$
for some elementary d-ary forest E. (Indeed, a priori y is of the form
$y=[T_-,g,F_+][E,1,1]_G$
for some elementary d-ary forest E. (Indeed, a priori y is of the form
![]() $[T_-,g,F_+][1,h,1][E,1,1]_G$
, but the above shows that we can ignore the
$[T_-,g,F_+][1,h,1][E,1,1]_G$
, but the above shows that we can ignore the
![]() $[1,h,1]$
factor for the purposes of characterizing y.) We conclude that for any x, there exist only finitely many y with
$[1,h,1]$
factor for the purposes of characterizing y.) We conclude that for any x, there exist only finitely many y with
![]() $x\preceq y$
. We refer to this property by saying that
$x\preceq y$
. We refer to this property by saying that
![]() $\mathscr {X}_d(G_*)$
is upward-locally finite.
$\mathscr {X}_d(G_*)$
is upward-locally finite.
Contractibility: To see that
![]() $\mathscr {X}_d(G_*)$
is contractible, we will show that the inclusion
$\mathscr {X}_d(G_*)$
is contractible, we will show that the inclusion
![]() $\mathscr {X}_d(G_*)\to |\mathscr {P}_d(G_*)|$
is a homotopy equivalence. Using the usual notation of open and closed intervals in posets, every simplex of
$\mathscr {X}_d(G_*)\to |\mathscr {P}_d(G_*)|$
is a homotopy equivalence. Using the usual notation of open and closed intervals in posets, every simplex of
![]() $|\mathscr {P}_d(G_*)|$
that is not in
$|\mathscr {P}_d(G_*)|$
that is not in
![]() $\mathscr {X}_d(G_*)$
lies in the realization of a closed interval
$\mathscr {X}_d(G_*)$
lies in the realization of a closed interval
![]() $[x,y]$
for
$[x,y]$
for
![]() $x=[T_-,g,F_+]_G\le y=[T_-,g,F_+][F,1,1]_G$
with F a nonelementary d-ary forest. Hence, it suffices to show that we can build up from
$x=[T_-,g,F_+]_G\le y=[T_-,g,F_+][F,1,1]_G$
with F a nonelementary d-ary forest. Hence, it suffices to show that we can build up from
![]() $\mathscr {X}_d(G_*)$
to
$\mathscr {X}_d(G_*)$
to
![]() $|\mathscr {P}_d(G_*)|$
by gluing in the realizations of such closed intervals in some way that never changes the homotopy type. Using the above notation, the order we will use is in increasing order of the quantity
$|\mathscr {P}_d(G_*)|$
by gluing in the realizations of such closed intervals in some way that never changes the homotopy type. Using the above notation, the order we will use is in increasing order of the quantity
![]() $h(y)-h(x)$
. Thus, when we glue in
$h(y)-h(x)$
. Thus, when we glue in
![]() $|[x,y]|$
, we do so along
$|[x,y]|$
, we do so along
![]() $|[x,y)|\cup |(x,y]|$
. This is the suspension of
$|[x,y)|\cup |(x,y]|$
. This is the suspension of
![]() $|(x,y)|$
, so it suffices to see that
$|(x,y)|$
, so it suffices to see that
![]() $|(x,y)|$
is contractible. For this, we can mimic the proof of [Reference Witzel and ZaremskyWZ18, Lemma 4.7], which is the
$|(x,y)|$
is contractible. For this, we can mimic the proof of [Reference Witzel and ZaremskyWZ18, Lemma 4.7], which is the
![]() $d=2$
case. Recall that a poset
$d=2$
case. Recall that a poset
![]() $(Y, \sqsubseteq )$
is called conically contractible if there is a
$(Y, \sqsubseteq )$
is called conically contractible if there is a
![]() $y_0$
in Y and a poset map
$y_0$
in Y and a poset map
![]() $g: Y \rightarrow Y$
such that
$g: Y \rightarrow Y$
such that
![]() $z \sqsubseteq g(z) \sqsupseteq y_0$
for all z in Y. A consequence of a poset being conically contractible is that its geometric realization is contractible. Since a poset and its opposite poset have isomorphic geometric realizations, we can also use the criterion
$z \sqsubseteq g(z) \sqsupseteq y_0$
for all z in Y. A consequence of a poset being conically contractible is that its geometric realization is contractible. Since a poset and its opposite poset have isomorphic geometric realizations, we can also use the criterion
![]() $z \sqsupseteq g(z) \sqsubseteq y_0$
. See the discussion in [Reference QuillenQui78, Section 1.5] for more details. Now, given any
$z \sqsupseteq g(z) \sqsubseteq y_0$
. See the discussion in [Reference QuillenQui78, Section 1.5] for more details. Now, given any
![]() $z \in (x,y]$
, define
$z \in (x,y]$
, define
![]() $g(z)$
to be the largest element of
$g(z)$
to be the largest element of
![]() $[x,z]$
such that
$[x,z]$
such that
![]() $x\preceq g(z)$
(the idea is to replace any d-ary forest with its unique largest elementary subforest). By our hypothesis,
$x\preceq g(z)$
(the idea is to replace any d-ary forest with its unique largest elementary subforest). By our hypothesis,
![]() $g(z)$
is in
$g(z)$
is in
![]() $[x,y)$
and it is also clearly in
$[x,y)$
and it is also clearly in
![]() $(x,y]$
, so we have
$(x,y]$
, so we have
![]() $g(z)\in (x,y)$
. Let
$g(z)\in (x,y)$
. Let
![]() $y_0=g(y).$
Note that for any
$y_0=g(y).$
Note that for any
![]() $z\in (x,y)$
, we have
$z\in (x,y)$
, we have
![]() $g(z) \le y_0$
. Therefore,
$g(z) \le y_0$
. Therefore,
![]() $z \ge g(z) \le y_0$
and
$z \ge g(z) \le y_0$
and
![]() $(x,y)$
is conically contractible.
$(x,y)$
is conically contractible.
Action and stabilizers: The group
![]() $\mathscr {T}_d(G_*)$
acts on
$\mathscr {T}_d(G_*)$
acts on
![]() $\mathscr {X}_d(G_*)$
by left multiplication, which is well defined since the equivalence relation defining vertices of
$\mathscr {X}_d(G_*)$
by left multiplication, which is well defined since the equivalence relation defining vertices of
![]() $\mathscr {X}_d(G_*)$
and the partial order dictating which vertices span cubes are both given by right multiplication. Note too that h is invariant under this action. We claim that the stabilizer of a vertex with h value m is isomorphic to
$\mathscr {X}_d(G_*)$
and the partial order dictating which vertices span cubes are both given by right multiplication. Note too that h is invariant under this action. We claim that the stabilizer of a vertex with h value m is isomorphic to
![]() $G_m$
. Given such a vertex
$G_m$
. Given such a vertex
![]() $[T_-,g,F_+]_G$
and an element
$[T_-,g,F_+]_G$
and an element
![]() $[U_-,h,U_+]$
of
$[U_-,h,U_+]$
of
![]() $\mathscr {T}_d(G_*)$
, we have
$\mathscr {T}_d(G_*)$
, we have
![]() $[U_-,h,U_+][T_-,g,F_+]_G=[T_-,g,F_+]_G$
if and only if
$[U_-,h,U_+][T_-,g,F_+]_G=[T_-,g,F_+]_G$
if and only if
![]() $[F_+,g^{-1},T_-][U_-,h,U_+][T_-,g,F_+]=[1,h',1]$
for some
$[F_+,g^{-1},T_-][U_-,h,U_+][T_-,g,F_+]=[1,h',1]$
for some
![]() $h'\in G_m$
(since
$h'\in G_m$
(since
![]() $F_+$
has m roots, the “
$F_+$
has m roots, the “
![]() $1$
” here is the trivial forest with m roots, and
$1$
” here is the trivial forest with m roots, and
![]() $h'\in G_m$
). Thus,
$h'\in G_m$
). Thus,
![]() $[U_-,h,U_+]\mapsto h'$
provides the desired isomorphism from the vertex stabilizer to
$[U_-,h,U_+]\mapsto h'$
provides the desired isomorphism from the vertex stabilizer to
![]() $G_m$
. Now we claim that any cube stabilizer is a finite index subgroup of a vertex stabilizer. Consider a cube in
$G_m$
. Now we claim that any cube stabilizer is a finite index subgroup of a vertex stabilizer. Consider a cube in
![]() $\mathscr {X}_d(G_*)$
, say with x its unique vertex with minimum h value and y its unique vertex with maximal h value. Since the action preserves h, the cube stabilizer lies in the stabilizer of the vertex x (and that of y). Since
$\mathscr {X}_d(G_*)$
, say with x its unique vertex with minimum h value and y its unique vertex with maximal h value. Since the action preserves h, the cube stabilizer lies in the stabilizer of the vertex x (and that of y). Since
![]() $\mathscr {X}_d(G_*)$
is upward-locally finite,
$\mathscr {X}_d(G_*)$
is upward-locally finite,
![]() $\operatorname {\mathrm {Symm}}(\{z\mid x\preceq z\})$
is finite, so the kernel of
$\operatorname {\mathrm {Symm}}(\{z\mid x\preceq z\})$
is finite, so the kernel of
![]() $\operatorname {\mathrm {Stab}}(x)\to \operatorname {\mathrm {Symm}}(\{z\mid x\preceq z\})$
has finite index in
$\operatorname {\mathrm {Stab}}(x)\to \operatorname {\mathrm {Symm}}(\{z\mid x\preceq z\})$
has finite index in
![]() $\operatorname {\mathrm {Stab}}(x)$
. This kernel clearly fixes our cube pointwise, so we conclude that the stabilizer of the cube has finite index in the stabilizer of x.
$\operatorname {\mathrm {Stab}}(x)$
. This kernel clearly fixes our cube pointwise, so we conclude that the stabilizer of the cube has finite index in the stabilizer of x.
Cocompactness: Let
![]() $\mathscr {X}_d(G_*)^{h\le m}$
be the full subcomplex of
$\mathscr {X}_d(G_*)^{h\le m}$
be the full subcomplex of
![]() $\mathscr {X}_d(G_*)$
spanned by vertices with at most m feet. Since h is invariant under the action of
$\mathscr {X}_d(G_*)$
spanned by vertices with at most m feet. Since h is invariant under the action of
![]() $\mathscr {T}_d(G_*)$
, all the
$\mathscr {T}_d(G_*)$
, all the
![]() $\mathscr {X}_d(G_*)^{h\le m}$
are stabilized by this action. Given vertices
$\mathscr {X}_d(G_*)^{h\le m}$
are stabilized by this action. Given vertices
![]() $[T_-,g,F_+]_G$
and
$[T_-,g,F_+]_G$
and
![]() $[U_-,h,E_+]_G$
with the same h value, the product
$[U_-,h,E_+]_G$
with the same h value, the product
![]() $[U_-,h,E_+][F_+,g^{-1},T_-]$
exists, lies in
$[U_-,h,E_+][F_+,g^{-1},T_-]$
exists, lies in
![]() $\mathscr {T}_d(G_*)$
, and takes
$\mathscr {T}_d(G_*)$
, and takes
![]() $[T_-,g,F_+]_G$
to
$[T_-,g,F_+]_G$
to
![]() $[U_-,h,E_+]_G$
. Hence,
$[U_-,h,E_+]_G$
. Hence,
![]() $\mathscr {T}_d(G_*)$
is transitive on vertices of a given h value. Since
$\mathscr {T}_d(G_*)$
is transitive on vertices of a given h value. Since
![]() $\mathscr {X}_d(G_*)$
is upward-locally finite, and since the vertices of any given
$\mathscr {X}_d(G_*)$
is upward-locally finite, and since the vertices of any given
![]() $\mathscr {X}_d(G_*)^{h\le m}$
only have finitely many h values, this shows that the action of
$\mathscr {X}_d(G_*)^{h\le m}$
only have finitely many h values, this shows that the action of
![]() $\mathscr {T}_d(G_*)$
on any
$\mathscr {T}_d(G_*)$
on any
![]() $\mathscr {X}_d(G_*)^{h\le m}$
is cocompact.
$\mathscr {X}_d(G_*)^{h\le m}$
is cocompact.
Let us summarize all of the above.
Proposition 4.2 The group
![]() $\mathscr {T}_d(G_*)$
acts on the contractible cube complex
$\mathscr {T}_d(G_*)$
acts on the contractible cube complex
![]() $\mathscr {X}_d(G_*)$
with cube stabilizers isomorphic to finite index subgroups of the
$\mathscr {X}_d(G_*)$
with cube stabilizers isomorphic to finite index subgroups of the
![]() $G_m$
. The action on each
$G_m$
. The action on each
![]() $\mathscr {X}_d(G_*)^{h\le m}$
is cocompact.
$\mathscr {X}_d(G_*)^{h\le m}$
is cocompact.
Remark 4.3 In [Reference SteinSZ21], there is a more general construction given for a self-similar group G, called the H-Stein–Farley complex for
![]() $H\le G$
, with the
$H\le G$
, with the
![]() $H=G$
case recovering the original Stein–Farley complex. One could also fully generalize the H-Stein–Farley complexes from [Reference SteinSZ21] as we have just done in the
$H=G$
case recovering the original Stein–Farley complex. One could also fully generalize the H-Stein–Farley complexes from [Reference SteinSZ21] as we have just done in the
![]() $H=G$
case, to some sort of
$H=G$
case, to some sort of
![]() $(H_*)$
-Stein–Farley complexes for
$(H_*)$
-Stein–Farley complexes for
![]() $H_m\le G_m$
. This would be quite technical and tedious in general, and besides getting the braided Röver group to be
$H_m\le G_m$
. This would be quite technical and tedious in general, and besides getting the braided Röver group to be
![]() $\operatorname {\mathrm {F}}_\infty $
, it is unclear what this would buy us at the moment. Hence, we will do this (in the following subsection) just for the braided Röver group, where we can follow the comparatively easier road map from [Reference Brady, Burillo, Cleary and SteinBM16].
$\operatorname {\mathrm {F}}_\infty $
, it is unclear what this would buy us at the moment. Hence, we will do this (in the following subsection) just for the braided Röver group, where we can follow the comparatively easier road map from [Reference Brady, Burillo, Cleary and SteinBM16].
4.2 Descending links
In this subsection and the next, we prove Theorem 4.1. In a now-standard approach, we will combine Proposition 4.2 with Brown’s Criterion and discrete Morse theory to reduce the problem to an analysis of descending links.
First, let us recall some background on discrete Morse theory and descending links in general. Let Y be an affine cell complex, in the sense of [Reference Bashwinger and ZaremskyBB97]. Let
![]() $h\, {\colon}\, Y\to \mathbb {R}$
be a map such that the image of the vertex set of Y is a closed, discrete subset of
$h\, {\colon}\, Y\to \mathbb {R}$
be a map such that the image of the vertex set of Y is a closed, discrete subset of
![]() $\mathbb {R}$
. If the restriction of h to every positive-dimensional cell is a nonconstant affine map, then we call h a Morse function. These conditions ensure that for every cell, there is a unique vertex at which h achieves its maximum value on that cell. The descending star
$\mathbb {R}$
. If the restriction of h to every positive-dimensional cell is a nonconstant affine map, then we call h a Morse function. These conditions ensure that for every cell, there is a unique vertex at which h achieves its maximum value on that cell. The descending star
![]() $\operatorname {st}^\downarrow \! v$
of a vertex v is the subcomplex of Y consisting of all cells for which v is this vertex with maximum h value. The descending link
$\operatorname {st}^\downarrow \! v$
of a vertex v is the subcomplex of Y consisting of all cells for which v is this vertex with maximum h value. The descending link
![]() $\operatorname {lk}^\downarrow \! v$
of v is the link of v in
$\operatorname {lk}^\downarrow \! v$
of v is the link of v in
![]() $\operatorname {st}^\downarrow \! v$
, i.e., the space of directions out of v along which h strictly decreases. (One could analogously define ascending stars and links, but here we will only use the descending version.)
$\operatorname {st}^\downarrow \! v$
, i.e., the space of directions out of v along which h strictly decreases. (One could analogously define ascending stars and links, but here we will only use the descending version.)
The point of Morse theory is that an understanding of the descending links can translate to an understanding of the whole complex. The following essentially combines the Morse Lemma from [Reference Bashwinger and ZaremskyBB97] with Brown’s Criterion from [Reference BrothierBro87], to produce a sufficient condition for a group to be of type
![]() $\operatorname {\mathrm {F}}_n$
. See [Reference SteinSZ21, Lemma 3.1] for an
$\operatorname {\mathrm {F}}_n$
. See [Reference SteinSZ21, Lemma 3.1] for an
![]() $\operatorname {\mathrm {F}}_\infty $
version of the following, which works exactly analogously for
$\operatorname {\mathrm {F}}_\infty $
version of the following, which works exactly analogously for
![]() $\operatorname {\mathrm {F}}_n$
.
$\operatorname {\mathrm {F}}_n$
.
Citation 4.4 (Brown’s Criterion plus discrete Morse theory)
Let
![]() $\Gamma $
be a group acting cellularly on an
$\Gamma $
be a group acting cellularly on an
![]() $(n-1)$
-connected CW complex X. Suppose that the stabilizer of any p-cell is of type
$(n-1)$
-connected CW complex X. Suppose that the stabilizer of any p-cell is of type
![]() $\operatorname {\mathrm {F}}_{n-p}$
. Let
$\operatorname {\mathrm {F}}_{n-p}$
. Let
![]() $h\, {\colon}\, X\to \mathbb {R}$
be a
$h\, {\colon}\, X\to \mathbb {R}$
be a
![]() $\Gamma $
-invariant Morse function such that the sublevel complexes
$\Gamma $
-invariant Morse function such that the sublevel complexes
![]() $X^{h\le m}$
are
$X^{h\le m}$
are
![]() $\Gamma $
-cocompact for each
$\Gamma $
-cocompact for each
![]() $m\in \mathbb {R}$
. If there exists
$m\in \mathbb {R}$
. If there exists
![]() $t\in \mathbb {R}$
such that for all
$t\in \mathbb {R}$
such that for all
![]() $x\in X^{(0)}$
with
$x\in X^{(0)}$
with
![]() $h(x)\ge t$
, we have that
$h(x)\ge t$
, we have that
![]() $\operatorname {lk}^\downarrow \! x$
is
$\operatorname {lk}^\downarrow \! x$
is
![]() $(n-1)$
-connected, then
$(n-1)$
-connected, then
![]() $\Gamma $
is of type
$\Gamma $
is of type
![]() $\operatorname {\mathrm {F}}_n$
.
$\operatorname {\mathrm {F}}_n$
.
Now let us discuss descending links in
![]() $\mathscr {X}_d(G_*)$
. Since
$\mathscr {X}_d(G_*)$
. Since
![]() $\mathscr {X}_d(G_*)$
is a cube complex, the link of a vertex v is a simplicial complex, with a k-simplex for each
$\mathscr {X}_d(G_*)$
is a cube complex, the link of a vertex v is a simplicial complex, with a k-simplex for each
![]() $(k+1)$
-cube containing v. The descending link is the subcomplex whose simplices correspond to cubes for which the vertex is the one with maximum h value, i.e., the most feet. Thus, a k-simplex in
$(k+1)$
-cube containing v. The descending link is the subcomplex whose simplices correspond to cubes for which the vertex is the one with maximum h value, i.e., the most feet. Thus, a k-simplex in
![]() $\operatorname {lk}^\downarrow \! v$
, say with
$\operatorname {lk}^\downarrow \! v$
, say with
![]() $h(v)=m$
, is represented by
$h(v)=m$
, is represented by
![]() $v[1,g,E]_G$
, for g some element of
$v[1,g,E]_G$
, for g some element of
![]() $G_m$
and E some elementary d-ary forest with m leaves and
$G_m$
and E some elementary d-ary forest with m leaves and
![]() $k+1$
carets. The face relation is given by removing carets from E. Note that the barycentric subdivision of
$k+1$
carets. The face relation is given by removing carets from E. Note that the barycentric subdivision of
![]() $\operatorname {lk}^\downarrow \! v$
is naturally a subcomplex of
$\operatorname {lk}^\downarrow \! v$
is naturally a subcomplex of
![]() $|\mathscr {P}_d(G_*)|$
, namely the full subcomplex spanned by all the
$|\mathscr {P}_d(G_*)|$
, namely the full subcomplex spanned by all the
![]() $v[1,g,E]_G$
.
$v[1,g,E]_G$
.
There is a convenient model for the descending links. Note that, up to the action of
![]() $\mathscr {T}_d(G_*)$
,
$\mathscr {T}_d(G_*)$
,
![]() $\operatorname {lk}^\downarrow \! v$
only depends on
$\operatorname {lk}^\downarrow \! v$
only depends on
![]() $h(v)$
. Thus, the following complex is isomorphic to every descending link of a vertex with m feet:
$h(v)$
. Thus, the following complex is isomorphic to every descending link of a vertex with m feet:
Definition 4.1 (Model for descending link)
Let
![]() $\mathscr {L}_d^m(G_*)$
be the simplicial complex with a k-simplex for each
$\mathscr {L}_d^m(G_*)$
be the simplicial complex with a k-simplex for each
![]() $[1,g,E]_G$
for
$[1,g,E]_G$
for
![]() $g\in G_m$
and E an elementary d-ary forest with m leaves and
$g\in G_m$
and E an elementary d-ary forest with m leaves and
![]() $k+1$
carets, with face relation given by removing carets from E.
$k+1$
carets, with face relation given by removing carets from E.
The culmination of Sections 4.1 and 4.2 is the following, which holds for any d-ary cloning system.
Proposition 4.5 Suppose that
![]() $G_m$
is of type
$G_m$
is of type
![]() $\operatorname {\mathrm {F}}_n$
for all m and that
$\operatorname {\mathrm {F}}_n$
for all m and that
![]() $\mathscr {L}_d^m(G_*)$
is
$\mathscr {L}_d^m(G_*)$
is
![]() $(n-1)$
-connected for all but finitely many m. Then
$(n-1)$
-connected for all but finitely many m. Then
![]() $\mathscr {T}_d(G_*)$
is of type
$\mathscr {T}_d(G_*)$
is of type
![]() $\operatorname {\mathrm {F}}_n$
.
$\operatorname {\mathrm {F}}_n$
.
Proof We look at
![]() $\mathscr {T}_d(G_*)$
acting on
$\mathscr {T}_d(G_*)$
acting on
![]() $\mathscr {X}_d(G_*)$
, with the Morse function h, and verify the requirements from Citation 4.4. By Proposition 4.2,
$\mathscr {X}_d(G_*)$
, with the Morse function h, and verify the requirements from Citation 4.4. By Proposition 4.2,
![]() $\mathscr {X}_d(G_*)$
is contractible (hence
$\mathscr {X}_d(G_*)$
is contractible (hence
![]() $(n-1)$
-connected), the stabilizer of any p-cube is isomorphic to a finite index subgroup of some
$(n-1)$
-connected), the stabilizer of any p-cube is isomorphic to a finite index subgroup of some
![]() $G_m$
, so is of type
$G_m$
, so is of type
![]() $\operatorname {\mathrm {F}}_n$
(hence
$\operatorname {\mathrm {F}}_n$
(hence
![]() $\operatorname {\mathrm {F}}_{n-p}$
) by assumption, and the sublevel complexes are all cocompact. Since
$\operatorname {\mathrm {F}}_{n-p}$
) by assumption, and the sublevel complexes are all cocompact. Since
![]() $\mathscr {L}_d^m(G_*)$
is
$\mathscr {L}_d^m(G_*)$
is
![]() $(n-1)$
-connected for all but finitely many m, the statement about descending links holds, and so we are done.
$(n-1)$
-connected for all but finitely many m, the statement about descending links holds, and so we are done.
4.3 Descending links in the braided case
Now we return to the special case from Section 3.3. We have a braided self-similar group
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
of type
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
of type
![]() $\operatorname {\mathrm {F}}_n$
, and need to prove that
$\operatorname {\mathrm {F}}_n$
, and need to prove that
![]() $\operatorname {br}\!V_d(G)=\mathscr {T}_d(B_*\wr G)$
is of type
$\operatorname {br}\!V_d(G)=\mathscr {T}_d(B_*\wr G)$
is of type
![]() $\operatorname {\mathrm {F}}_n$
. As indicated by Proposition 4.5, the key thing to show is that
$\operatorname {\mathrm {F}}_n$
. As indicated by Proposition 4.5, the key thing to show is that
![]() $\mathscr {L}_d^m(B_*\wr G)$
is
$\mathscr {L}_d^m(B_*\wr G)$
is
![]() $(n-1)$
-connected for all but finitely many m. To analyze the higher connectivity of
$(n-1)$
-connected for all but finitely many m. To analyze the higher connectivity of
![]() $\mathscr {L}_d^m(B_*\wr G)$
, we will use a strategy that essentially comes from [Reference Benli, Grigorchuk and de la HarpeBFM+16] in the case when
$\mathscr {L}_d^m(B_*\wr G)$
, we will use a strategy that essentially comes from [Reference Benli, Grigorchuk and de la HarpeBFM+16] in the case when
![]() $G=\{1\}$
and
$G=\{1\}$
and
![]() $d=2$
, and more generally from [Reference Skipper and ZaremskySW] in the case when G is braided self-identical.
$d=2$
, and more generally from [Reference Skipper and ZaremskySW] in the case when G is braided self-identical.
The idea is to map
![]() $\mathscr {L}_d^m(B_*\wr G)$
to a complex that is easier to understand. We will use the following complex, considered in [Reference Skipper and ZaremskySW].
$\mathscr {L}_d^m(B_*\wr G)$
to a complex that is easier to understand. We will use the following complex, considered in [Reference Skipper and ZaremskySW].
Definition 4.2 (d-marked point disk complex)
Let
![]() $\mathcal {S}_{b,m}^g$
be a surface with b boundary components, m marked points, and genus g. The d-marked-point-disk complex
$\mathcal {S}_{b,m}^g$
be a surface with b boundary components, m marked points, and genus g. The d-marked-point-disk complex
![]() ${\mathbb {D}}_d(\mathcal {S}_{b,m}^g)$
is the simplicial complex defined as follows. A k-simplex is an isotopy class of
${\mathbb {D}}_d(\mathcal {S}_{b,m}^g)$
is the simplicial complex defined as follows. A k-simplex is an isotopy class of
![]() $k+1$
disjointly embedded disks such that each disk encloses precisely d marked points in its interior and has no marked points in its boundary. (Here, whenever we say “isotopy,” it is implicit that all the intermediate maps in the isotopy must satisfy these rules as well, e.g., marked points cannot drift out of the interior of the disk and then back in.) The face relation is given by taking subsets.
$k+1$
disjointly embedded disks such that each disk encloses precisely d marked points in its interior and has no marked points in its boundary. (Here, whenever we say “isotopy,” it is implicit that all the intermediate maps in the isotopy must satisfy these rules as well, e.g., marked points cannot drift out of the interior of the disk and then back in.) The face relation is given by taking subsets.
Remark 4.6 This complex is related to the curve complex first defined by Harvey in [Reference HarveyHar81], namely, outside some low-complexity cases,
![]() ${\mathbb {D}}_d(\mathcal {S}_{b,m}^g)$
can be viewed as a full subcomplex of the curve complex. Indeed, given a disk enclosing d marked points, we can take its boundary curve, which “usually” gives a vertex in the curve complex. This fails if the boundary curve bounds a disk, a punctured sphere, or an annulus on the other side, which can only happen if
${\mathbb {D}}_d(\mathcal {S}_{b,m}^g)$
can be viewed as a full subcomplex of the curve complex. Indeed, given a disk enclosing d marked points, we can take its boundary curve, which “usually” gives a vertex in the curve complex. This fails if the boundary curve bounds a disk, a punctured sphere, or an annulus on the other side, which can only happen if
![]() $m\le d+1$
. It might also happen that two disks are disjoint up to isotopy, but their boundary curves are isotopic, which can happen when
$m\le d+1$
. It might also happen that two disks are disjoint up to isotopy, but their boundary curves are isotopic, which can happen when
![]() $m=2d$
.
$m=2d$
.
Our next goal is to map
![]() $\mathscr {L}_d^m(B_*\wr G)$
to
$\mathscr {L}_d^m(B_*\wr G)$
to
![]() ${\mathbb {D}}_d(\mathcal {S}_{1,m}^0)$
in a certain way. First, we describe a useful alternate viewpoint of elementary d-ary forests. Let
${\mathbb {D}}_d(\mathcal {S}_{1,m}^0)$
in a certain way. First, we describe a useful alternate viewpoint of elementary d-ary forests. Let
![]() $L_{m-1}$
be the linear graph with m vertices, that is, the graph with m vertices labeled
$L_{m-1}$
be the linear graph with m vertices, that is, the graph with m vertices labeled
![]() $1$
to m, and
$1$
to m, and
![]() $m-1$
edges, one connecting i to
$m-1$
edges, one connecting i to
![]() $i+1$
for each
$i+1$
for each
![]() $1\le i<m$
. Call a subgraph of
$1\le i<m$
. Call a subgraph of
![]() $L_{m-1}$
a d-matching on
$L_{m-1}$
a d-matching on
![]() $L_{m-1}$
if each of its connected components is a subgraph of length
$L_{m-1}$
if each of its connected components is a subgraph of length
![]() $d-1$
. The set of d-matchings forms a simplicial complex called the d-matching complex, denoted by
$d-1$
. The set of d-matchings forms a simplicial complex called the d-matching complex, denoted by
![]() ${\mathcal {M}}_d(L_{m-1})$
, where a matching forms a k-simplex whenever it consists of
${\mathcal {M}}_d(L_{m-1})$
, where a matching forms a k-simplex whenever it consists of
![]() $k+1$
disjoint paths, and the face relation is given by inclusion. Observe that there is a bijection between the set of elementary d-ary forests with m leaves and the set of d-matchings on
$k+1$
disjoint paths, and the face relation is given by inclusion. Observe that there is a bijection between the set of elementary d-ary forests with m leaves and the set of d-matchings on
![]() $L_{m-1}$
. Under the identification, d-carets correspond to paths of length
$L_{m-1}$
. Under the identification, d-carets correspond to paths of length
![]() $d-1$
. See Figure 5 for example.
$d-1$
. See Figure 5 for example.

Figure 5: An example of the bijective correspondence between elementary
![]() $3$
-ary forests with nine leaves and simplices of
$3$
-ary forests with nine leaves and simplices of
![]() ${\mathcal {M}}_3(L_{8})$
.
${\mathcal {M}}_3(L_{8})$
.
Let
![]() $\mathcal {S}_m=\mathcal {S}_{1,m}^0$
be the unit disk with m marked points given by fixing an embedding
$\mathcal {S}_m=\mathcal {S}_{1,m}^0$
be the unit disk with m marked points given by fixing an embedding
![]() $L_{m-1} \hookrightarrow \mathcal {S}_m$
of the linear graph with
$L_{m-1} \hookrightarrow \mathcal {S}_m$
of the linear graph with
![]() $m-1$
edges into
$m-1$
edges into
![]() $\mathcal {S}_{1,m}^0$
(so the marked points are the images of the vertices). The braid group
$\mathcal {S}_{1,m}^0$
(so the marked points are the images of the vertices). The braid group
![]() $B_m$
on m strands is isomorphic to the mapping class group of the disk with m marked points [Reference BirmanBir75], so we have an action of
$B_m$
on m strands is isomorphic to the mapping class group of the disk with m marked points [Reference BirmanBir75], so we have an action of
![]() $B_m$
on
$B_m$
on
![]() ${\mathbb {D}}_{d}(\mathcal {S}_m)$
, which will be convenient to take to be a right action.
${\mathbb {D}}_{d}(\mathcal {S}_m)$
, which will be convenient to take to be a right action.
Define a map
![]() $\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \rightarrow {\mathbb {D}}_{d}(\mathcal {S}_m)$
as follows. For
$\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \rightarrow {\mathbb {D}}_{d}(\mathcal {S}_m)$
as follows. For
![]() $[1, \beta (f_1, \dots , f_m), E]_G$
a simplex in
$[1, \beta (f_1, \dots , f_m), E]_G$
a simplex in
![]() $\mathscr {L}_d^m(B_*\wr G)$
, first view the elementary d-ary forest E as a d-matching in
$\mathscr {L}_d^m(B_*\wr G)$
, first view the elementary d-ary forest E as a d-matching in
![]() ${\mathcal {M}}_d(L_{m-1})$
as above. Then take a disk tubular neighborhood of the d-matching, call it
${\mathcal {M}}_d(L_{m-1})$
as above. Then take a disk tubular neighborhood of the d-matching, call it
![]() $D_E$
, to obtain a simplex in
$D_E$
, to obtain a simplex in
![]() ${\mathbb {D}}_{d}(\mathcal {S}_m)$
. Forget the labels
${\mathbb {D}}_{d}(\mathcal {S}_m)$
. Forget the labels
![]() $(f_1, \dots , f_m)$
, and then act on
$(f_1, \dots , f_m)$
, and then act on
![]() $D_E$
by applying
$D_E$
by applying
![]() $\beta ^{-1}$
on the right. In this way, we obtain a simplicial map
$\beta ^{-1}$
on the right. In this way, we obtain a simplicial map
 $$ \begin{align*} \mu \, {\colon}\, \mathscr{L}_d^m(B_*\wr G) & \to {\mathbb {D}}_{d}(\mathcal{S}_m) \\ [1, \beta (f_1, \dots, f_m), E]_G & \mapsto (D_E)\beta^{-1} \text{ .} \end{align*} $$
$$ \begin{align*} \mu \, {\colon}\, \mathscr{L}_d^m(B_*\wr G) & \to {\mathbb {D}}_{d}(\mathcal{S}_m) \\ [1, \beta (f_1, \dots, f_m), E]_G & \mapsto (D_E)\beta^{-1} \text{ .} \end{align*} $$
Lemma 4.7 The map
![]() $\mu $
is well defined.
$\mu $
is well defined.
Proof Say E has q roots. Let
![]() $\gamma (g_1,\dots ,g_q)\in B_q\wr G$
, so
$\gamma (g_1,\dots ,g_q)\in B_q\wr G$
, so
Let
![]() $\gamma '(g_1',\dots ,g_m')\in B_q\wr G$
and
$\gamma '(g_1',\dots ,g_m')\in B_q\wr G$
and
![]() $E'$
be such that
$E'$
be such that
Then
for some
![]() $f_i'$
, so
$f_i'$
, so
![]() $\mu $
sends this to
$\mu $
sends this to
![]() $(D_{E'})(\beta \gamma ')^{-1}$
. We need to show that this equals
$(D_{E'})(\beta \gamma ')^{-1}$
. We need to show that this equals
![]() $(D_E)\beta ^{-1}$
, or equivalently that
$(D_E)\beta ^{-1}$
, or equivalently that
![]() $(D_{E'})(\gamma ')^{-1}=D_E$
, i.e.,
$(D_{E'})(\gamma ')^{-1}=D_E$
, i.e.,
![]() $(D_E)\gamma '=D_{E'}$
. Note that
$(D_E)\gamma '=D_{E'}$
. Note that
![]() $\gamma '$
is obtained by taking
$\gamma '$
is obtained by taking
![]() $\gamma $
, turning each strand corresponding to a root of E with a d-caret on it into d parallel strands (call this intermediate braid
$\gamma $
, turning each strand corresponding to a root of E with a d-caret on it into d parallel strands (call this intermediate braid
![]() $\gamma "$
), and then on each such collection of d parallel strands applying some
$\gamma "$
), and then on each such collection of d parallel strands applying some
![]() $\phi (g_i)\in B_d$
to it (where
$\phi (g_i)\in B_d$
to it (where
![]() $\phi $
is as in Section 2.1). When acting on
$\phi $
is as in Section 2.1). When acting on
![]() $D_E$
though, since each of these local copies of the
$D_E$
though, since each of these local copies of the
![]() $\phi (g_i)$
is supported in the interior of one of the disks in the disk system, they do not change the (equivalence class of the) disk system. It is clear that
$\phi (g_i)$
is supported in the interior of one of the disks in the disk system, they do not change the (equivalence class of the) disk system. It is clear that
![]() $(D_E)\gamma "=D_{E'}$
, so we conclude that also
$(D_E)\gamma "=D_{E'}$
, so we conclude that also
![]() $(D_E)\gamma '=D_{E'}$
.
$(D_E)\gamma '=D_{E'}$
.
One can visualize
![]() $\mu $
as taking
$\mu $
as taking
![]() $[1,\beta (f_1,\dots ,f_n),E]_G$
, viewing it as the braid
$[1,\beta (f_1,\dots ,f_n),E]_G$
, viewing it as the braid
![]() $\beta $
with strands labeled by the
$\beta $
with strands labeled by the
![]() $f_i$
at the bottom and with E serving to “merge” strands together, and then forgetting the labels
$f_i$
at the bottom and with E serving to “merge” strands together, and then forgetting the labels
![]() $f_i$
, considering the merges as d-matchings, enlarging them to disks, “combing straight” the braid, and seeing where the disks are taken. See Figure 6 for example. Note that the resulting simplex
$f_i$
, considering the merges as d-matchings, enlarging them to disks, “combing straight” the braid, and seeing where the disks are taken. See Figure 6 for example. Note that the resulting simplex
![]() $(D_E)\beta ^{-1}$
of
$(D_E)\beta ^{-1}$
of
![]() ${\mathbb {D}}_{d}(\mathcal {S}_m)$
has the same dimension as the simplex
${\mathbb {D}}_{d}(\mathcal {S}_m)$
has the same dimension as the simplex
![]() $[1, \beta (f_1, \dots , f_m), E]_G$
of
$[1, \beta (f_1, \dots , f_m), E]_G$
of
![]() $\mathscr {L}_d^m(B_*\wr G)$
, so in particular
$\mathscr {L}_d^m(B_*\wr G)$
, so in particular
![]() $\mu $
is simplexwise injective. Also, note that if
$\mu $
is simplexwise injective. Also, note that if
![]() $d>2$
, then the
$d>2$
, then the
![]() $\phi (g_i)$
from the proof of Lemma 4.7 could change the d-matchings, but cannot change their corresponding disks, hence why we use disk complexes instead of, say, arc complexes.
$\phi (g_i)$
from the proof of Lemma 4.7 could change the d-matchings, but cannot change their corresponding disks, hence why we use disk complexes instead of, say, arc complexes.

Figure 6: An illustration of
![]() $\mu \, {\colon}\, \mathscr {L}_3^6(B_*\wr G) \rightarrow {\mathbb {D}}_3(\mathcal {S}_6)$
. The successive pictures show the process of flattening to a
$\mu \, {\colon}\, \mathscr {L}_3^6(B_*\wr G) \rightarrow {\mathbb {D}}_3(\mathcal {S}_6)$
. The successive pictures show the process of flattening to a
![]() $3$
-matching, expanding the matching to disks, forgetting the labels, and “combing straight” the braid.
$3$
-matching, expanding the matching to disks, forgetting the labels, and “combing straight” the braid.
In the following proofs, we will need a useful tool introduced by Hatcher and Wahl called the complete join [Reference Hatcher and WahlHW10].
Definition 4.3 (Complete join [complex)
] A surjective simplicial map
![]() $\nu : Y\to X$
is called a complete join if it satisfies the following properties:
$\nu : Y\to X$
is called a complete join if it satisfies the following properties:
-
(1)
 $\nu $
is simplexwise injective.
$\nu $
is simplexwise injective. -
(2) For each k-simplex
 $\sigma $
of X, say with vertices
$\sigma $
of X, say with vertices
 $v_0,\dots ,v_k$
, the fiber
$v_0,\dots ,v_k$
, the fiber
 $\nu ^{-1}(\sigma )$
equals the join
$\nu ^{-1}(\sigma )$
equals the join
 $\nu ^{-1}(v_0)\ast \cdots \ast \nu ^{-1}(v_k)$
.
$\nu ^{-1}(v_0)\ast \cdots \ast \nu ^{-1}(v_k)$
.
In this case, we call Y a complete join complex over X.
Definition 4.4 (Weakly Cohen–Macaulay)
A simplicial complex X is called weakly Cohen–Macaulay (wCM) of dimension n if X is
![]() $(n-1)$
-connected and the link of each k-simplex of X is
$(n-1)$
-connected and the link of each k-simplex of X is
![]() $(n-k-2)$
-connected. (Note that X need not necessarily be n-dimensional.)
$(n-k-2)$
-connected. (Note that X need not necessarily be n-dimensional.)
The main result regarding complete joins that we will use is the following.
Citation 4.8 [Reference Hatcher and WahlHW10, Proposition 3.5]
If Y is a complete join complex over a complex X that is wCM of dimension n, then Y is also wCM of dimension n.
Now we would like to use the map
![]() $\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \to {\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
to prove higher connectivity of
$\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \to {\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
to prove higher connectivity of
![]() $\mathscr {L}_d^m(B_*\wr G)$
, and hence of the descending links in the Stein–Farley complex. First, we need the following, which is proved in [Reference Skipper and ZaremskySW].
$\mathscr {L}_d^m(B_*\wr G)$
, and hence of the descending links in the Stein–Farley complex. First, we need the following, which is proved in [Reference Skipper and ZaremskySW].
Citation 4.9 [Reference Skipper and ZaremskySW]
For any
![]() $d\ge 2$
, the complex
$d\ge 2$
, the complex
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is
${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is
![]() $\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -2\Big )$
-connected.
$\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -2\Big )$
-connected.
Corollary 4.10 For any
![]() $d\ge 2$
, the complex
$d\ge 2$
, the complex
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
![]() $\lfloor \frac {m+1}{2d-1}\rfloor -1$
.
$\lfloor \frac {m+1}{2d-1}\rfloor -1$
.
Proof Since
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is
${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
is
![]() $\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -2\Big )$
-connected by Citation 4.9, we just need to prove that the link of any k-simplex is
$\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -2\Big )$
-connected by Citation 4.9, we just need to prove that the link of any k-simplex is
![]() $\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -k-3\Big )$
-connected. Let
$\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -k-3\Big )$
-connected. Let
![]() $\sigma =\{D_0,\dots ,D_k\}$
be a k-simplex in
$\sigma =\{D_0,\dots ,D_k\}$
be a k-simplex in
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
. Let
${\mathbb {D}}_{d}(\mathcal {S}_{b,m}^g)$
. Let
![]() $S'$
be the surface obtained from
$S'$
be the surface obtained from
![]() $\mathcal {S}_{b,m}^g$
by removing the interiors of the
$\mathcal {S}_{b,m}^g$
by removing the interiors of the
![]() $D_i$
, including the
$D_i$
, including the
![]() $d(k+1)$
many marked points in their interiors, leaving
$d(k+1)$
many marked points in their interiors, leaving
![]() $k+1$
new boundary components. Since the
$k+1$
new boundary components. Since the
![]() $D_i$
are pairwise disjoint,
$D_i$
are pairwise disjoint,
![]() $S'$
is connected, and hence is of the form
$S'$
is connected, and hence is of the form
![]() $\mathcal {S}_{b+(k+1),m-d(k+1)}^g$
. The link of
$\mathcal {S}_{b+(k+1),m-d(k+1)}^g$
. The link of
![]() $\sigma $
is, therefore, isomorphic to
$\sigma $
is, therefore, isomorphic to
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{b+(k+1),m-d(k+1)}^g)$
, which is
${\mathbb {D}}_{d}(\mathcal {S}_{b+(k+1),m-d(k+1)}^g)$
, which is
![]() $\Big (\left \lfloor \frac {m-d(k+1)+1}{2d-1}\right \rfloor -2\Big )$
-connected by Citation 4.9. Since
$\Big (\left \lfloor \frac {m-d(k+1)+1}{2d-1}\right \rfloor -2\Big )$
-connected by Citation 4.9. Since
![]() $\frac {-d(k+1)}{2d-1}\ge -(k+1)$
, this is also
$\frac {-d(k+1)}{2d-1}\ge -(k+1)$
, this is also
![]() $\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -k-3\Big )$
-connected, so we are done.
$\Big (\left \lfloor \frac {m+1}{2d-1}\right \rfloor -k-3\Big )$
-connected, so we are done.
Proposition 4.11 For any
![]() $d\ge 2$
and any
$d\ge 2$
and any
![]() $m\in \mathbb {N}$
, the complex
$m\in \mathbb {N}$
, the complex
![]() $\mathscr {L}_d^m(B_*\wr G)$
is wCM of dimension
$\mathscr {L}_d^m(B_*\wr G)$
is wCM of dimension
![]() $\lfloor \frac {m+1}{2d-1}\rfloor -1$
, so in particular is
$\lfloor \frac {m+1}{2d-1}\rfloor -1$
, so in particular is
![]() $(\lfloor \frac {m+1}{2d-1}\rfloor -2)$
-connected.
$(\lfloor \frac {m+1}{2d-1}\rfloor -2)$
-connected.
Proof Since
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is wCM of dimension
${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is wCM of dimension
![]() $\lfloor \frac {m+1}{2d-1}\rfloor -1$
by Corollary 4.10, it suffices by Citation 4.8 to prove that
$\lfloor \frac {m+1}{2d-1}\rfloor -1$
by Corollary 4.10, it suffices by Citation 4.8 to prove that
![]() $\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \to {\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is a complete join. We know that
$\mu \, {\colon}\, \mathscr {L}_d^m(B_*\wr G) \to {\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is a complete join. We know that
![]() $\mu $
is surjective and simplexwise injective. Now we need to show that the fiber under
$\mu $
is surjective and simplexwise injective. Now we need to show that the fiber under
![]() $\mu $
of any simplex in
$\mu $
of any simplex in
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is the join of the fibers of its vertices. Clearly, the fiber of the simplex lies in the join of the vertex fibers, so we need to prove the reverse inclusion. This means that we need to prove that any collection of
${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
is the join of the fibers of its vertices. Clearly, the fiber of the simplex lies in the join of the vertex fibers, so we need to prove the reverse inclusion. This means that we need to prove that any collection of
![]() $k+1$
vertices in
$k+1$
vertices in
![]() $\mathscr {L}_d^m(B_*\wr G)$
whose images under
$\mathscr {L}_d^m(B_*\wr G)$
whose images under
![]() $\mu $
span a k-simplex in
$\mu $
span a k-simplex in
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
themselves span a k-simplex in
${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
themselves span a k-simplex in
![]() $\mathscr {L}_d^m(B_*\wr G)$
. We induct on k. The base case
$\mathscr {L}_d^m(B_*\wr G)$
. We induct on k. The base case
![]() $k=0$
is trivial, so assume
$k=0$
is trivial, so assume
![]() $k\ge 1$
. Let
$k\ge 1$
. Let
![]() $v_0,\dots ,v_k$
be
$v_0,\dots ,v_k$
be
![]() $k+1$
vertices in
$k+1$
vertices in
![]() $\mathscr {L}_d^m(B_*\wr G)$
whose images under
$\mathscr {L}_d^m(B_*\wr G)$
whose images under
![]() $\mu $
span a k-simplex in
$\mu $
span a k-simplex in
![]() ${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
. By induction,
${\mathbb {D}}_{d}(\mathcal {S}_{1,m}^0)$
. By induction,
![]() $v_1,\dots ,v_k$
span a
$v_1,\dots ,v_k$
span a
![]() $(k-1)$
-simplex, call it
$(k-1)$
-simplex, call it
![]() $\sigma $
. Now
$\sigma $
. Now
![]() $\mu (\sigma )$
is a collection of k pairwise disjoint disks, and
$\mu (\sigma )$
is a collection of k pairwise disjoint disks, and
![]() $\mu (v_0)$
is a disk disjoint from all the disks in
$\mu (v_0)$
is a disk disjoint from all the disks in
![]() $\mu (\sigma )$
. Up to the left action of
$\mu (\sigma )$
. Up to the left action of
![]() $B_m\wr G$
on
$B_m\wr G$
on
![]() $\mathscr {L}_d^m(B_*\wr G)$
, we can assume without loss of generality that
$\mathscr {L}_d^m(B_*\wr G)$
, we can assume without loss of generality that
![]() $\sigma $
is of the form
$\sigma $
is of the form
![]() $[1,1,E]_G$
for some E. Now say
$[1,1,E]_G$
for some E. Now say
![]() ${v_0=[1,\beta (f_1,\dots ,f_m),e]_G}$
for some
${v_0=[1,\beta (f_1,\dots ,f_m),e]_G}$
for some
![]() $\beta (f_1,\dots ,f_m)\in B_m\wr G$
and e some elementary d-ary forest with exactly one d-caret. Since
$\beta (f_1,\dots ,f_m)\in B_m\wr G$
and e some elementary d-ary forest with exactly one d-caret. Since
![]() $\mu (\sigma )=D_E$
is disjoint from
$\mu (\sigma )=D_E$
is disjoint from
![]() $\mu (v_0)=(D_e)\beta ^{-1}$
, we know that
$\mu (v_0)=(D_e)\beta ^{-1}$
, we know that
![]() $[1,\beta (f_1,\dots ,f_m),E]_G=[1,1,E]_G$
. Setting
$[1,\beta (f_1,\dots ,f_m),E]_G=[1,1,E]_G$
. Setting
![]() $E'$
equal to the elementary d-ary forest obtained as the union of E and e, we therefore have that
$E'$
equal to the elementary d-ary forest obtained as the union of E and e, we therefore have that
![]() $[1,\beta (f_1,\dots ,f_m),E']_G$
is a k-simplex containing both
$[1,\beta (f_1,\dots ,f_m),E']_G$
is a k-simplex containing both
![]() $\sigma $
and
$\sigma $
and
![]() $v_0$
.
$v_0$
.
Now we can prove Theorem 4.1.
Proof of Theorem 4.1
We have a braided self-similar group
![]() $G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
of type
$G\le \operatorname {br}\!\operatorname {\mathrm {Aut}}(\mathcal {T}_d)$
of type
![]() $\operatorname {\mathrm {F}}_n$
, and need to prove that
$\operatorname {\mathrm {F}}_n$
, and need to prove that
![]() $\operatorname {br}\!V_d(G)=\mathscr {T}_d(B_*\wr G)$
is of type
$\operatorname {br}\!V_d(G)=\mathscr {T}_d(B_*\wr G)$
is of type
![]() $\operatorname {\mathrm {F}}_n$
. Note that G being of type
$\operatorname {\mathrm {F}}_n$
. Note that G being of type
![]() $\operatorname {\mathrm {F}}_n$
implies each
$\operatorname {\mathrm {F}}_n$
implies each
![]() $B_m\wr G$
is of type
$B_m\wr G$
is of type
![]() $\operatorname {\mathrm {F}}_n$
, since a direct product of finitely many type
$\operatorname {\mathrm {F}}_n$
, since a direct product of finitely many type
![]() $\operatorname {\mathrm {F}}_n$
groups is of type
$\operatorname {\mathrm {F}}_n$
groups is of type
![]() $\operatorname {\mathrm {F}}_n$
, and an extension of a type
$\operatorname {\mathrm {F}}_n$
, and an extension of a type
![]() $\operatorname {\mathrm {F}}_n$
group (like
$\operatorname {\mathrm {F}}_n$
group (like
![]() $B_d$
) by a type
$B_d$
) by a type
![]() $\operatorname {\mathrm {F}}_n$
group is type
$\operatorname {\mathrm {F}}_n$
group is type
![]() $\operatorname {\mathrm {F}}_n$
(see, e.g., [Reference Genevois, Lonjou and UrechGeo08, Theorem 7.2.21]). Hence, by Proposition 4.5, we just need to prove that
$\operatorname {\mathrm {F}}_n$
(see, e.g., [Reference Genevois, Lonjou and UrechGeo08, Theorem 7.2.21]). Hence, by Proposition 4.5, we just need to prove that
![]() $\mathscr {L}_d^m(B_*\wr G)$
is
$\mathscr {L}_d^m(B_*\wr G)$
is
![]() $(n-1)$
-connected for all but finitely many m. This follows from Proposition 4.11, since
$(n-1)$
-connected for all but finitely many m. This follows from Proposition 4.11, since
![]() $\lfloor \frac {m+1}{2d-1}\rfloor -2$
goes to
$\lfloor \frac {m+1}{2d-1}\rfloor -2$
goes to
![]() $\infty $
with m.
$\infty $
with m.
5 Finiteness properties of the braided Röver group
This section is entirely about the braided Röver group
![]() $\operatorname {br}\!V_2(\operatorname {\mathrm {brGrig}})$
. For brevity, let us write
$\operatorname {br}\!V_2(\operatorname {\mathrm {brGrig}})$
. For brevity, let us write
![]() $\operatorname {br}\!R$
for the group, and we will also introduce other concise notation as we go. The main result of this section is the following.
$\operatorname {br}\!R$
for the group, and we will also introduce other concise notation as we go. The main result of this section is the following.
Theorem 5.1 The braided Röver group
![]() $\operatorname {br}\!R$
is of type
$\operatorname {br}\!R$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
.
$\operatorname {\mathrm {F}}_\infty $
.
Note that
![]() $\operatorname {\mathrm {brGrig}}$
is not even finitely presented (Lemma 2.14) much less
$\operatorname {\mathrm {brGrig}}$
is not even finitely presented (Lemma 2.14) much less
![]() $\operatorname {\mathrm {F}}_\infty $
, so Theorem 4.1 does not apply. In particular,
$\operatorname {\mathrm {F}}_\infty $
, so Theorem 4.1 does not apply. In particular,
![]() $\operatorname {br}\!R$
shows that the converse of Theorem 4.1 is not true in general, in contrast to the braided self-identical case done in [Reference Skipper and ZaremskySW]. Our road map is Belk and Matucci’s proof that the Röver group
$\operatorname {br}\!R$
shows that the converse of Theorem 4.1 is not true in general, in contrast to the braided self-identical case done in [Reference Skipper and ZaremskySW]. Our road map is Belk and Matucci’s proof that the Röver group
![]() $V_2(\operatorname {\mathrm {Grig}})$
is of type
$V_2(\operatorname {\mathrm {Grig}})$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
[Reference Brady, Burillo, Cleary and SteinBM16]. We will also make use of the constructions from Section 4.
$\operatorname {\mathrm {F}}_\infty $
[Reference Brady, Burillo, Cleary and SteinBM16]. We will also make use of the constructions from Section 4.
To begin, we return to the groupoid
of elements of the form
![]() $[F_-,g,F_+]$
, for
$[F_-,g,F_+]$
, for
![]() $F_\pm $
forests with m leaves and
$F_\pm $
forests with m leaves and
![]() $g\in B_m\wr \operatorname {\mathrm {brGrig}}$
. (In this section, all trees and forests are binary.) As before, consider elements of the form
$g\in B_m\wr \operatorname {\mathrm {brGrig}}$
. (In this section, all trees and forests are binary.) As before, consider elements of the form
![]() $[T_-,g,F_+]$
(for
$[T_-,g,F_+]$
(for
![]() $T_-$
a tree), and mod out an equivalence relation given by right multiplication by elements of the form
$T_-$
a tree), and mod out an equivalence relation given by right multiplication by elements of the form
![]() $[1,g',1]$
, but this time only do so for
$[1,g',1]$
, but this time only do so for
![]() $g=\beta (f_1,\dots ,f_m)$
with
$g=\beta (f_1,\dots ,f_m)$
with
The reason for doing this is that
![]() $Z\cong \mathbb {Z}^2$
is of type
$Z\cong \mathbb {Z}^2$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
, unlike
$\operatorname {\mathrm {F}}_\infty $
, unlike
![]() $\operatorname {\mathrm {brGrig}}$
itself. Write
$\operatorname {\mathrm {brGrig}}$
itself. Write
for the resulting equivalence classes, and write
![]() $\sim _Z$
for the equivalence relation.
$\sim _Z$
for the equivalence relation.
As before, define a partial order on these equivalence classes
![]() $[\tau ]_Z$
(for
$[\tau ]_Z$
(for
![]() $\tau $
a triple of the form
$\tau $
a triple of the form
![]() $\tau =(T_-,g,F_+)$
) by declaring that
$\tau =(T_-,g,F_+)$
) by declaring that
![]() $[\tau ]_Z \le [\tau ][F,1,1]_Z$
for any forest F with m roots. Note that we must account for changing representatives up to
$[\tau ]_Z \le [\tau ][F,1,1]_Z$
for any forest F with m roots. Note that we must account for changing representatives up to
![]() $\sim _Z$
, so we moreover have
$\sim _Z$
, so we moreover have
![]() $[\tau ]_Z \le [\tau ][1,g',1][F,1,1]_Z$
for any
$[\tau ]_Z \le [\tau ][1,g',1][F,1,1]_Z$
for any
![]() $g'\in B_m\wr Z$
. This is not transitive as defined, since we must account for changing representatives up to
$g'\in B_m\wr Z$
. This is not transitive as defined, since we must account for changing representatives up to
![]() $\sim _Z$
, so we actually take the transitive closure. Thus, an upper bound of
$\sim _Z$
, so we actually take the transitive closure. Thus, an upper bound of
![]() $[\tau ]_Z$
looks like
$[\tau ]_Z$
looks like
![]() $[\tau ][F_1,g_1',1]\cdots [F_k,g_k',1]_Z$
for
$[\tau ][F_1,g_1',1]\cdots [F_k,g_k',1]_Z$
for
![]() $F_i$
some forests and
$F_i$
some forests and
![]() $g_i'$
elements of the relevant braid groups wreathed with Z (not with all of
$g_i'$
elements of the relevant braid groups wreathed with Z (not with all of
![]() $\operatorname {\mathrm {brGrig}}$
, to reiterate). Write
$\operatorname {\mathrm {brGrig}}$
, to reiterate). Write
![]() $\mathscr {P}_2(B_*\wr \operatorname {\mathrm {brGrig}})_Z$
for this poset, or
$\mathscr {P}_2(B_*\wr \operatorname {\mathrm {brGrig}})_Z$
for this poset, or
![]() $\mathscr {P}_Z$
for short.
$\mathscr {P}_Z$
for short.
Lemma 5.2 For any
![]() $g\in B_q\wr \operatorname {\mathrm {brGrig}}$
, there exists a forest F such that
$g\in B_q\wr \operatorname {\mathrm {brGrig}}$
, there exists a forest F such that
![]() $[1,g,1][F,1,1]=[F',g',1]$
for some
$[1,g,1][F,1,1]=[F',g',1]$
for some
![]() $F'$
and some
$F'$
and some
![]() $g'$
not only in
$g'$
not only in
![]() $B_m\wr \operatorname {\mathrm {brGrig}}$
but even in
$B_m\wr \operatorname {\mathrm {brGrig}}$
but even in
![]() $B_m\wr Z$
for appropriate m.
$B_m\wr Z$
for appropriate m.
Proof Intuitively, this means that we can apply successive braided wreath recursions to g until all the “a”s are gone.
First, note that if
![]() $g\in B_q$
, then the result holds for any F, not just some F, so without loss of generality g has no “braid part”, i.e.,
$g\in B_q$
, then the result holds for any F, not just some F, so without loss of generality g has no “braid part”, i.e.,
![]() $g\in \prod _q\operatorname {\mathrm {brGrig}}$
(and at this point the desired
$g\in \prod _q\operatorname {\mathrm {brGrig}}$
(and at this point the desired
![]() $F'$
will be F). Now, clearly, without loss of generality,
$F'$
will be F). Now, clearly, without loss of generality,
![]() $q=1$
, so
$q=1$
, so
![]() $g\in \operatorname {\mathrm {brGrig}}$
, and we are looking for a tree T such that
$g\in \operatorname {\mathrm {brGrig}}$
, and we are looking for a tree T such that
![]() $[1,g,1][T,1,1]=[T,g',1]$
for
$[1,g,1][T,1,1]=[T,g',1]$
for
![]() $g'\in B_m\wr Z$
. Write
$g'\in B_m\wr Z$
. Write
for
![]() $z_i\in Z$
and
$z_i\in Z$
and
![]() $k_i\in \mathbb {Z}$
, as a reduced expression in the sense of Lemma 2.11. We will induct on the length of this expression. If the length is
$k_i\in \mathbb {Z}$
, as a reduced expression in the sense of Lemma 2.11. We will induct on the length of this expression. If the length is
![]() $1$
and
$1$
and
![]() $g\in Z$
, we can just take T to be trivial, and if the length is
$g\in Z$
, we can just take T to be trivial, and if the length is
![]() $1$
and g is a power of a, then we can take T to be a single caret. Now assume that the length is greater than
$1$
and g is a power of a, then we can take T to be a single caret. Now assume that the length is greater than
![]() $1$
. Let
$1$
. Let
![]() $\wedge $
be the tree with one caret, so
$\wedge $
be the tree with one caret, so
![]() $[1,g,1]=[\wedge ,(g)\kappa _1^1,\wedge ]$
. We have that
$[1,g,1]=[\wedge ,(g)\kappa _1^1,\wedge ]$
. We have that
![]() $(g)\kappa _1^1$
is of the form
$(g)\kappa _1^1$
is of the form
![]() $\zeta ^k(g_1,g_2)$
for some
$\zeta ^k(g_1,g_2)$
for some
![]() $k\in \mathbb {Z}$
and
$k\in \mathbb {Z}$
and
![]() $g_1,g_2\in \operatorname {\mathrm {brGrig}}$
, and by Lemma 2.11 the length of each of
$g_1,g_2\in \operatorname {\mathrm {brGrig}}$
, and by Lemma 2.11 the length of each of
![]() $g_1$
and
$g_1$
and
![]() $g_2$
is less than that of g. By induction, we can therefore choose a tree T such that
$g_2$
is less than that of g. By induction, we can therefore choose a tree T such that
![]() $[1,g,1]=[T,g',T]$
with
$[1,g,1]=[T,g',T]$
with
![]() $g'\in B_m\wr Z$
for some m. Now
$g'\in B_m\wr Z$
for some m. Now
![]() $[1,g,1][T,1,1]=[T,g',1]$
as desired.
$[1,g,1][T,1,1]=[T,g',1]$
as desired.
Corollary 5.3 The poset
![]() $\mathscr {P}_Z$
is directed, so its geometric realization is contractible.
$\mathscr {P}_Z$
is directed, so its geometric realization is contractible.
Proof Let
![]() $[T_-,g,F_+]_Z$
and
$[T_-,g,F_+]_Z$
and
![]() $[U_-,h,D_+]_Z$
be elements of
$[U_-,h,D_+]_Z$
be elements of
![]() $\mathscr {P}_Z$
. Up to taking upper bounds, we can assume that
$\mathscr {P}_Z$
. Up to taking upper bounds, we can assume that
![]() $F_+$
and
$F_+$
and
![]() $D_+$
are trivial. Now observe that thanks to Lemma 5.2, there exist forests F and
$D_+$
are trivial. Now observe that thanks to Lemma 5.2, there exist forests F and
![]() $F'$
such that
$F'$
such that
![]() $[1,g,1][F,1,1]=[F',g',1]$
for
$[1,g,1][F,1,1]=[F',g',1]$
for
![]() $g'$
not only in
$g'$
not only in
![]() $B_m\wr \operatorname {\mathrm {brGrig}}$
(for appropriate m) but even in
$B_m\wr \operatorname {\mathrm {brGrig}}$
(for appropriate m) but even in
![]() $B_m\wr Z$
. Hence,
$B_m\wr Z$
. Hence,
![]() $[1,g,1][F,1,1]_Z=[F',1,1]_Z$
. This shows that, up to taking upper bounds, we can assume that g and h are trivial. At this point, our elements are
$[1,g,1][F,1,1]_Z=[F',1,1]_Z$
. This shows that, up to taking upper bounds, we can assume that g and h are trivial. At this point, our elements are
![]() $[T_-,1,1]_Z$
and
$[T_-,1,1]_Z$
and
![]() $[U_-,1,1]_Z$
, which clearly have an common upper bound.
$[U_-,1,1]_Z$
, which clearly have an common upper bound.
Our next goal is to construct an analog of the Stein–Farley complex. It will no longer have a cubical structure, but it will have a polysimplicial structure. First, we need some definitions and notation.
Definition 5.1 (Direct sum)
Given braids
![]() $\beta \in B_m$
and
$\beta \in B_m$
and
![]() $\beta '\in B_{m'}$
, the direct sum
$\beta '\in B_{m'}$
, the direct sum
![]() $\beta \oplus \beta '$
is the element of
$\beta \oplus \beta '$
is the element of
![]() $B_{m+m'}$
obtained by setting
$B_{m+m'}$
obtained by setting
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
next to each other, so the first m strands braid according to
$\beta '$
next to each other, so the first m strands braid according to
![]() $\beta $
, and the last
$\beta $
, and the last
![]() $m'$
strands braid according to
$m'$
strands braid according to
![]() $\beta '$
. Given a forest F with q roots and a forest
$\beta '$
. Given a forest F with q roots and a forest
![]() $F'$
with
$F'$
with
![]() $q'$
roots, the direct sum
$q'$
roots, the direct sum
![]() $F\oplus F'$
is the forest with
$F\oplus F'$
is the forest with
![]() $q+q'$
roots whose first q trees comprise F and whose last
$q+q'$
roots whose first q trees comprise F and whose last
![]() $q'$
trees comprise
$q'$
trees comprise
![]() $F'$
. Now let
$F'$
. Now let
![]() $[F_-,g,F_+],[F_-',g',F_+']\in \mathscr {G}$
. Say
$[F_-,g,F_+],[F_-',g',F_+']\in \mathscr {G}$
. Say
![]() $g=\beta (f_1,\dots ,f_m)$
and
$g=\beta (f_1,\dots ,f_m)$
and
![]() $g'=\beta '(f_1',\dots ,f^{\prime }_{m'})$
. Let
$g'=\beta '(f_1',\dots ,f^{\prime }_{m'})$
. Let
![]() $F_-"=F_-\oplus F_-'$
, let
$F_-"=F_-\oplus F_-'$
, let
![]() $F_+"=F_+\oplus F_+'$
, let
$F_+"=F_+\oplus F_+'$
, let
![]() $\beta "=\beta \oplus \beta '$
, and let
$\beta "=\beta \oplus \beta '$
, and let
![]() $g"=\beta "(f_1,\dots ,f_m,f_1',\dots ,f^{\prime }_{m'})$
. Then the direct sum
$g"=\beta "(f_1,\dots ,f_m,f_1',\dots ,f^{\prime }_{m'})$
. Then the direct sum
![]() $[F_-,g,F_+]\oplus [F_-',g',F_+']$
is the element
$[F_-,g,F_+]\oplus [F_-',g',F_+']$
is the element
![]() $[F_-",g",F_+"]$
of
$[F_-",g",F_+"]$
of
![]() $\mathscr {G}$
.
$\mathscr {G}$
.
Definition 5.2 (Splitting, simple splitting)
Call an element of
![]() $\mathscr {G}$
of the form
$\mathscr {G}$
of the form
for
![]() $g_i\in B_{m_i}\wr Z$
(for appropriate
$g_i\in B_{m_i}\wr Z$
(for appropriate
![]() $m_i$
) a splitting, so in the poset
$m_i$
) a splitting, so in the poset
![]() $\mathscr {P}_Z$
we have
$\mathscr {P}_Z$
we have
![]() $[\tau ]_Z\le [\tau ]\Delta _Z$
for any splitting
$[\tau ]_Z\le [\tau ]\Delta _Z$
for any splitting
![]() $\Delta $
. Call this a one-head splitting if
$\Delta $
. Call this a one-head splitting if
![]() $F_1$
is a tree. A simple splitting is one that is
$F_1$
is a tree. A simple splitting is one that is
![]() $\sim _Z$
-equivalent to a direct sum of finitely many copies of
$\sim _Z$
-equivalent to a direct sum of finitely many copies of
![]() $1$
together with a one-head splitting
$1$
together with a one-head splitting
![]() $\Delta $
. Intuitively, a splitting is simple if only one “head” actually gets split. Note that every splitting is a product of simple splittings.
$\Delta $
. Intuitively, a splitting is simple if only one “head” actually gets split. Note that every splitting is a product of simple splittings.
Definition 5.3 (Weakly elementary)
Write
![]() $\wedge $
for the tree with one caret. Write
$\wedge $
for the tree with one caret. Write
![]() $\wedge ^2$
for the tree obtained from
$\wedge ^2$
for the tree obtained from
![]() $\wedge $
by adding a caret to its left leaf. Call a splitting weakly elementary if it is
$\wedge $
by adding a caret to its left leaf. Call a splitting weakly elementary if it is
![]() $\sim _Z$
-equivalent to a direct sum of finitely many splittings, each of which is of one of the following forms:
$\sim _Z$
-equivalent to a direct sum of finitely many splittings, each of which is of one of the following forms:
Let us abuse notation and write
![]() $1=[1,1,1]$
,
$1=[1,1,1]$
,
![]() $\wedge (a^k,1)=[\wedge ,(a^k,1),1]$
, and
$\wedge (a^k,1)=[\wedge ,(a^k,1),1]$
, and
![]() $\wedge ^2=[\wedge ^2,1,1]$
, so the weakly elementary splittings are those that are
$\wedge ^2=[\wedge ^2,1,1]$
, so the weakly elementary splittings are those that are
![]() $\sim _Z$
-equivalent to direct sums of copies of
$\sim _Z$
-equivalent to direct sums of copies of
![]() $1$
,
$1$
,
![]() $\wedge (a^k,1)$
(
$\wedge (a^k,1)$
(
![]() $k\in \mathbb {Z}$
), and
$k\in \mathbb {Z}$
), and
![]() $\wedge ^2$
.
$\wedge ^2$
.
Note that the splitting
![]() $[1,b^k,1][\wedge ,(1,c^{-k}),1]$
equals
$[1,b^k,1][\wedge ,(1,c^{-k}),1]$
equals
![]() $[\wedge ,(a^k,c^k),\wedge ][\wedge ,(1,c^{-k}),1] = \wedge (a^k,1)$
, so
$[\wedge ,(a^k,c^k),\wedge ][\wedge ,(1,c^{-k}),1] = \wedge (a^k,1)$
, so
![]() $\wedge (a^k,1)$
really is a splitting. Also, note that any weakly elementary simple splitting is
$\wedge (a^k,1)$
really is a splitting. Also, note that any weakly elementary simple splitting is
![]() $\sim _Z$
-equivalent to a direct sum of finitely many copies of
$\sim _Z$
-equivalent to a direct sum of finitely many copies of
![]() $1$
together with a single splitting of the form
$1$
together with a single splitting of the form
![]() $1$
,
$1$
,
![]() $\wedge (a^k,1)$
for some
$\wedge (a^k,1)$
for some
![]() $k\in \mathbb {Z}$
, or
$k\in \mathbb {Z}$
, or
![]() $\wedge ^2$
.
$\wedge ^2$
.
For
![]() $[\tau ]_Z\in \mathscr {P}_Z$
and
$[\tau ]_Z\in \mathscr {P}_Z$
and
![]() $\Delta $
a splitting such that the product
$\Delta $
a splitting such that the product
![]() $[\tau ]\Delta $
makes sense, so
$[\tau ]\Delta $
makes sense, so
![]() $[\tau ]_Z\le [\tau ]\Delta _Z$
, write
$[\tau ]_Z\le [\tau ]\Delta _Z$
, write
![]() $[\tau ]_Z\trianglelefteq [\tau ]\Delta _Z$
if
$[\tau ]_Z\trianglelefteq [\tau ]\Delta _Z$
if
![]() $\Delta $
is weakly elementary. Call a simplex in
$\Delta $
is weakly elementary. Call a simplex in
![]() $|\mathscr {P}_Z|$
weakly elementary if it is of the form
$|\mathscr {P}_Z|$
weakly elementary if it is of the form
![]() $x_0<\cdots <x_k$
with
$x_0<\cdots <x_k$
with
![]() $x_i\trianglelefteq x_j$
for all
$x_i\trianglelefteq x_j$
for all
![]() $i<j$
. The weakly elementary simplices form a subcomplex of
$i<j$
. The weakly elementary simplices form a subcomplex of
![]() $|\mathscr {P}_Z|$
. We will denote this subcomplex by
$|\mathscr {P}_Z|$
. We will denote this subcomplex by
![]() $\mathscr {X}_2(B_*\wr \operatorname {\mathrm {brGrig}})_Z$
, or
$\mathscr {X}_2(B_*\wr \operatorname {\mathrm {brGrig}})_Z$
, or
![]() $\mathscr {X}_Z$
for short, and call it the Z-Stein–Farley complex for the braided Röver group. (Later we will identify
$\mathscr {X}_Z$
for short, and call it the Z-Stein–Farley complex for the braided Röver group. (Later we will identify
![]() $\mathscr {X}_Z$
with a polysimplicial complex that is more akin to the Stein–Farley cube complexes constructed earlier for general d-ary cloning systems.)
$\mathscr {X}_Z$
with a polysimplicial complex that is more akin to the Stein–Farley cube complexes constructed earlier for general d-ary cloning systems.)
Proposition 5.4 The Z-Stein–Farley complex
![]() $\mathscr {X}_Z$
is contractible.
$\mathscr {X}_Z$
is contractible.
Proof We can follow the argument in Section 4.1 that the usual Stein–Farley complex for a d-ary cloning system is contractible, in exactly the same way, and reduce the problem to proving that the realization
![]() $|(x,y)|$
is contractible, for any
$|(x,y)|$
is contractible, for any
![]() $x\le y$
in
$x\le y$
in
![]() $\mathscr {P}_Z$
with
$\mathscr {P}_Z$
with
![]() $x\not \trianglelefteq y$
. This in turn will follow by the same argument as in Section 4.1, provided we can show that for any
$x\not \trianglelefteq y$
. This in turn will follow by the same argument as in Section 4.1, provided we can show that for any
![]() $x\le y$
with
$x\le y$
with
![]() $x\not \trianglelefteq y$
there exists a unique largest
$x\not \trianglelefteq y$
there exists a unique largest
![]() $y_0\in (x,y)$
such that
$y_0\in (x,y)$
such that
![]() $x\trianglelefteq y_0$
. Without loss of generality,
$x\trianglelefteq y_0$
. Without loss of generality,
![]() $x=1$
. Analogously to the proofs of Lemma 4.7 and Proposition 4.8 of [Reference Brady, Burillo, Cleary and SteinBM16] (for the Röver group), it suffices to prove that if we have both
$x=1$
. Analogously to the proofs of Lemma 4.7 and Proposition 4.8 of [Reference Brady, Burillo, Cleary and SteinBM16] (for the Röver group), it suffices to prove that if we have both
![]() $\wedge (a^k,1)_Z\le y$
and
$\wedge (a^k,1)_Z\le y$
and
![]() $\wedge (a^\ell ,1)_Z\le y$
for some
$\wedge (a^\ell ,1)_Z\le y$
for some
![]() $k\ne \ell $
, then
$k\ne \ell $
, then
![]() $\wedge ^2_Z\le y$
. Let
$\wedge ^2_Z\le y$
. Let
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta '$
be splittings such that
$\Delta '$
be splittings such that
![]() $\wedge (a^k,1)\Delta _Z=y$
and
$\wedge (a^k,1)\Delta _Z=y$
and
![]() $\wedge (a^\ell ,1)\Delta ^(\prime )_Z=y$
, so
$\wedge (a^\ell ,1)\Delta ^(\prime )_Z=y$
, so
![]() $\wedge (a^k,1)\Delta _Z=\wedge (a^\ell ,1)\Delta ^(\prime )_Z$
. Thus,
$\wedge (a^k,1)\Delta _Z=\wedge (a^\ell ,1)\Delta ^(\prime )_Z$
. Thus,
![]() $\Delta ^{-1}(a^{\ell -k},1)\Delta '\in B_m\wr Z$
for appropriate m (identifying
$\Delta ^{-1}(a^{\ell -k},1)\Delta '\in B_m\wr Z$
for appropriate m (identifying
![]() $B_m\wr Z$
with its image in
$B_m\wr Z$
with its image in
![]() $\mathscr {G}$
under
$\mathscr {G}$
under
![]() $g\mapsto [1,g,1]$
). Now note that if
$g\mapsto [1,g,1]$
). Now note that if
![]() $\wedge ^2_Z\not \le y$
, then we have
$\wedge ^2_Z\not \le y$
, then we have
![]() $\Delta =z\oplus \overline {\Delta }$
and
$\Delta =z\oplus \overline {\Delta }$
and
![]() $\Delta '=z'\oplus \overline {\Delta }'$
for some
$\Delta '=z'\oplus \overline {\Delta }'$
for some
![]() $z,z'\in Z$
and some splittings
$z,z'\in Z$
and some splittings
![]() $\overline {\Delta }$
and
$\overline {\Delta }$
and
![]() $\overline {\Delta }'$
(that is, neither
$\overline {\Delta }'$
(that is, neither
![]() $\Delta $
nor
$\Delta $
nor
![]() $\Delta '$
can involve “splitting the first head”). But then,
$\Delta '$
can involve “splitting the first head”). But then,
![]() $\Delta ^{-1}(a^{\ell -k},1)\Delta '$
is the direct sum of
$\Delta ^{-1}(a^{\ell -k},1)\Delta '$
is the direct sum of
![]() $z^{-1}a^{\ell -k}z'$
with some element of
$z^{-1}a^{\ell -k}z'$
with some element of
![]() $B_{m-1}\wr Z$
, which implies
$B_{m-1}\wr Z$
, which implies
![]() $z^{-1}a^{\ell -k}z'\in Z$
, a contradiction since
$z^{-1}a^{\ell -k}z'\in Z$
, a contradiction since
![]() $a^{\ell -k}\not \in Z$
. We conclude that
$a^{\ell -k}\not \in Z$
. We conclude that
![]() $\wedge ^2_Z\le y$
.
$\wedge ^2_Z\le y$
.
5.1 Polysimplicial structure
Now let us describe the polysimplicial structure on
![]() $\mathscr {X}_Z$
. A polysimplex is a euclidean polytope that is a product of simplices. A polysimplicial complex is an affine cell complex whose cells are polysimplices, and such that any two cells intersect in a (possibly empty) common face of each. Polysimplicial complexes are a simultaneous generalization of simplicial and cubical complexes. The polysimplicial structure on
$\mathscr {X}_Z$
. A polysimplex is a euclidean polytope that is a product of simplices. A polysimplicial complex is an affine cell complex whose cells are polysimplices, and such that any two cells intersect in a (possibly empty) common face of each. Polysimplicial complexes are a simultaneous generalization of simplicial and cubical complexes. The polysimplicial structure on
![]() $\mathscr {X}_Z$
is built out of the following pieces.
$\mathscr {X}_Z$
is built out of the following pieces.
Definition 5.4 (Basic polysimplex, bottom vertex)
Let
![]() $[\tau ]_Z$
be a vertex in
$[\tau ]_Z$
be a vertex in
![]() $\mathscr {X}_Z$
, say with
$\mathscr {X}_Z$
, say with
![]() $h([\tau ]_Z)=m$
(here h is the “number of feet” function from before). For each
$h([\tau ]_Z)=m$
(here h is the “number of feet” function from before). For each
![]() ${1\le i\le m}$
, let
${1\le i\le m}$
, let
![]() $S_i$
be one of the following sets:
$S_i$
be one of the following sets:
Then the corresponding basic polysimplex
![]() $\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
is the full subcomplex of
$\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
is the full subcomplex of
![]() $\mathscr {X}_Z$
spanned by the vertex set
$\mathscr {X}_Z$
spanned by the vertex set
The bottom vertex of this basic polysimplex is
![]() $[\tau ]_Z$
.
$[\tau ]_Z$
.
Note that
![]() $\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
is a subdivision of a product of simplices, one for each
$\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
is a subdivision of a product of simplices, one for each
![]() $S_i$
, where the dimension of the simplex corresponding to
$S_i$
, where the dimension of the simplex corresponding to
![]() $S_i$
is
$S_i$
is
![]() $|S_i|-1$
. In particular, it makes sense to view this as a polysimplex.
$|S_i|-1$
. In particular, it makes sense to view this as a polysimplex.
It is clear that every weakly elementary simplex lies in some basic polysimplex, so the basic polysimplices cover
![]() $\mathscr {X}_Z$
. To see that the basic polysimplices form a polysimplicial complex with
$\mathscr {X}_Z$
. To see that the basic polysimplices form a polysimplicial complex with
![]() $\mathscr {X}_Z$
as a simplicial subdivision, it remains to show that any intersection of two basic polysimplices is a common face of each. Before proving this, we need a definition.
$\mathscr {X}_Z$
as a simplicial subdivision, it remains to show that any intersection of two basic polysimplices is a common face of each. Before proving this, we need a definition.
Definition 5.5 (Depth, nonexpanding)
For a forest F, the depth of a leaf is the distance from the leaf to the root of the tree in F containing the leaf. Let
![]() $[F_-,\beta (g_1,\dots ,g_m),F_+]\in \mathscr {G}$
. Call this groupoid element nonexpanding at the jth foot if for every leaf of the jth tree of
$[F_-,\beta (g_1,\dots ,g_m),F_+]\in \mathscr {G}$
. Call this groupoid element nonexpanding at the jth foot if for every leaf of the jth tree of
![]() $F_+$
, say it is the ith leaf of
$F_+$
, say it is the ith leaf of
![]() $F_+$
, we have that the depth of the ith leaf in
$F_+$
, we have that the depth of the ith leaf in
![]() $F_+$
is at most the depth of the
$F_+$
is at most the depth of the
![]() $\pi (\beta )(i)$
th leaf of
$\pi (\beta )(i)$
th leaf of
![]() $F_-$
. (Note that this property is invariant under expansions and reductions, so is well defined on elements of
$F_-$
. (Note that this property is invariant under expansions and reductions, so is well defined on elements of
![]() $\mathscr {G}$
.) If an element is nonexpanding at the jth foot for all j, call it nonexpanding.
$\mathscr {G}$
.) If an element is nonexpanding at the jth foot for all j, call it nonexpanding.
The terminology “nonexpanding” is inspired by the nonbraided case, as in [Reference Brady, Burillo, Cleary and SteinBM16], where groupoid elements are homeomorphisms between disjoint unions of copies of the Cantor set.
Lemma 5.5 Any intersection of two basic polysimplices is a common face of each.
Proof The proof of Lemma 5.3 of [Reference Brady, Burillo, Cleary and SteinBM16] for the Röver group can almost be copied verbatim for the braided case (up to changing notation and some left/right conventions), with just one step requiring justification, which we will point out when we reach it. Let
![]() $P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
and
$P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
and
![]() $Q=\operatorname {\mathrm {poly}}([\omega ];T_1,\dots ,T_q)$
be basic polysimplices. Each
$Q=\operatorname {\mathrm {poly}}([\omega ];T_1,\dots ,T_q)$
be basic polysimplices. Each
![]() $S_i$
has a natural total order, consistent with
$S_i$
has a natural total order, consistent with
![]() $\le $
in
$\le $
in
![]() $\mathscr {P}_Z$
when considered up to the “mod Z” equivalence relation, so it makes sense to take the minimum of a collection of elements of a given
$\mathscr {P}_Z$
when considered up to the “mod Z” equivalence relation, so it makes sense to take the minimum of a collection of elements of a given
![]() $S_i$
. Define a binary operation
$S_i$
. Define a binary operation
![]() $\wedge _P$
on the vertices of P via
$\wedge _P$
on the vertices of P via

Define
![]() $\wedge _Q$
analogously. If
$\wedge _Q$
analogously. If
![]() $P\cap Q=\emptyset $
, we are done, so suppose not. Let
$P\cap Q=\emptyset $
, we are done, so suppose not. Let
![]() $v,v'\in P\cap Q$
, and we claim
$v,v'\in P\cap Q$
, and we claim
![]() $v\wedge _P v'=v\wedge _Q v'$
. Without loss of generality,
$v\wedge _P v'=v\wedge _Q v'$
. Without loss of generality,
![]() $v\wedge _P v'=[\tau ]_Z$
and
$v\wedge _P v'=[\tau ]_Z$
and
![]() $v\wedge _Q v'=[\omega ]_Z$
. Choose
$v\wedge _Q v'=[\omega ]_Z$
. Choose
![]() $\Delta _i,\Delta _i'\in S_i$
and
$\Delta _i,\Delta _i'\in S_i$
and
![]() $\Omega _i,\Omega _i'\in T_i$
such that
$\Omega _i,\Omega _i'\in T_i$
such that
 $$ \begin{align*} &v=[\tau](\Delta_1\oplus\cdots\oplus\Delta_m)_Z=[\omega](\Omega_1\oplus\cdots\oplus\Omega_q)_Z\\ \text{ and } &v'=[\tau](\Delta_1'\oplus\cdots\oplus\Delta_m')_Z=[\omega](\Omega_1'\oplus\cdots\oplus\Omega_q')_Z \text{.} \end{align*} $$
$$ \begin{align*} &v=[\tau](\Delta_1\oplus\cdots\oplus\Delta_m)_Z=[\omega](\Omega_1\oplus\cdots\oplus\Omega_q)_Z\\ \text{ and } &v'=[\tau](\Delta_1'\oplus\cdots\oplus\Delta_m')_Z=[\omega](\Omega_1'\oplus\cdots\oplus\Omega_q')_Z \text{.} \end{align*} $$
Now, for appropriate r and p, choose
![]() $\beta \in B_r$
,
$\beta \in B_r$
,
![]() $\beta '\in B_p$
, and
$\beta '\in B_p$
, and
![]() $z_1,\dots ,z_r,z_1',\dots ,z_p'\in Z$
such that
$z_1,\dots ,z_r,z_1',\dots ,z_p'\in Z$
such that
 $$ \begin{align*} &[\tau](\Delta_1\oplus\cdots\oplus\Delta_m)=[\omega](\Omega_1\oplus\cdots\oplus\Omega_q)\beta(z_1,\dots,z_r)\\ \text{ and } &[\tau](\Delta_1'\oplus\cdots\oplus\Delta_m')=[\omega](\Omega_1'\oplus\cdots\oplus\Omega_q')\beta(z_1',\dots,z_p') \text{.} \end{align*} $$
$$ \begin{align*} &[\tau](\Delta_1\oplus\cdots\oplus\Delta_m)=[\omega](\Omega_1\oplus\cdots\oplus\Omega_q)\beta(z_1,\dots,z_r)\\ \text{ and } &[\tau](\Delta_1'\oplus\cdots\oplus\Delta_m')=[\omega](\Omega_1'\oplus\cdots\oplus\Omega_q')\beta(z_1',\dots,z_p') \text{.} \end{align*} $$
(As before, we identify
![]() $B_r\wr Z$
and
$B_r\wr Z$
and
![]() $B_p\wr Z$
with their images in
$B_p\wr Z$
with their images in
![]() $\mathscr {G}$
under
$\mathscr {G}$
under
![]() $g\mapsto [1,g,1]$
.) Solving for
$g\mapsto [1,g,1]$
.) Solving for
![]() $[\omega ]^{-1}[\tau ]$
in each equation yields
$[\omega ]^{-1}[\tau ]$
in each equation yields
 $$ \begin{align*} [\omega]^{-1}[\tau] &= (\Omega_1\oplus\cdots\oplus\Omega_q)\beta(z_1,\dots,z_r)(\Delta_1\oplus\cdots\oplus\Delta_m)^{-1} \\ &=(\Omega_1'\oplus\cdots\oplus\Omega_q')\beta'(z_1',\dots,z_p')(\Delta_1'\oplus\cdots\oplus\Delta_m')^{-1} \text{.} \end{align*} $$
$$ \begin{align*} [\omega]^{-1}[\tau] &= (\Omega_1\oplus\cdots\oplus\Omega_q)\beta(z_1,\dots,z_r)(\Delta_1\oplus\cdots\oplus\Delta_m)^{-1} \\ &=(\Omega_1'\oplus\cdots\oplus\Omega_q')\beta'(z_1',\dots,z_p')(\Delta_1'\oplus\cdots\oplus\Delta_m')^{-1} \text{.} \end{align*} $$
We want to conclude that
![]() $[\tau ]_Z=[\omega ]_Z$
, and this is the one step that cannot be copied verbatim from the nonbraided case. However, it does work analogously, using the above definition of nonexpanding. Since
$[\tau ]_Z=[\omega ]_Z$
, and this is the one step that cannot be copied verbatim from the nonbraided case. However, it does work analogously, using the above definition of nonexpanding. Since
![]() $v\wedge _P v'=[\tau ]_Z$
, we either have
$v\wedge _P v'=[\tau ]_Z$
, we either have
![]() $\Delta _i=1$
or
$\Delta _i=1$
or
![]() $\Delta _i'=1$
for each i. This shows that
$\Delta _i'=1$
for each i. This shows that
![]() $[\omega ]^{-1}[\tau ]$
is nonexpanding. Analogously,
$[\omega ]^{-1}[\tau ]$
is nonexpanding. Analogously,
![]() $[\tau ]^{-1}[\omega ]$
is nonexpanding. The only way this can happen, given the options for the
$[\tau ]^{-1}[\omega ]$
is nonexpanding. The only way this can happen, given the options for the
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Omega _i$
, is if every
$\Omega _i$
, is if every
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Omega _i$
is trivial. We conclude that
$\Omega _i$
is trivial. We conclude that
![]() $[\tau ]_Z=[\omega ]_Z$
, so
$[\tau ]_Z=[\omega ]_Z$
, so
![]() $\wedge _P$
and
$\wedge _P$
and
![]() $\wedge _Q$
agree when restricted to
$\wedge _Q$
agree when restricted to
![]() $P\cap Q$
. By the exact same argument as in the proof of [Reference Brady, Burillo, Cleary and SteinBM16, Lemma 5.3], this shows that without loss of generality,
$P\cap Q$
. By the exact same argument as in the proof of [Reference Brady, Burillo, Cleary and SteinBM16, Lemma 5.3], this shows that without loss of generality,
![]() $[\tau ]=[\omega ]$
, and
$[\tau ]=[\omega ]$
, and
![]() $P\cap Q=\operatorname {\mathrm {poly}}([\tau ];S_1\cap T_1,\dots ,S_m\cap T_m)$
, which is a common face of both P and Q.
$P\cap Q=\operatorname {\mathrm {poly}}([\tau ];S_1\cap T_1,\dots ,S_m\cap T_m)$
, which is a common face of both P and Q.
At this point, we can view
![]() $\mathscr {X}_Z$
either with its simplicial structure, or with this new polysimplicial structure. We will write
$\mathscr {X}_Z$
either with its simplicial structure, or with this new polysimplicial structure. We will write
![]() $\mathscr {X}_Z$
for both, and no confusion should arise.
$\mathscr {X}_Z$
for both, and no confusion should arise.
Lemma 5.6 Any stabilizer in
![]() $\operatorname {br}\!R$
of a polysimplex in
$\operatorname {br}\!R$
of a polysimplex in
![]() $\mathscr {X}_Z$
is of type
$\mathscr {X}_Z$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
.
$\operatorname {\mathrm {F}}_\infty $
.
Proof First, note that the stabilizer of any vertex in
![]() $\mathscr {X}_Z$
with h value m is isomorphic to
$\mathscr {X}_Z$
with h value m is isomorphic to
![]() $B_m\wr Z$
, by the same argument as in Section 4.1 for
$B_m\wr Z$
, by the same argument as in Section 4.1 for
![]() $\mathscr {X}_d(G_*)$
. Since
$\mathscr {X}_d(G_*)$
. Since
![]() $\mathscr {X}_Z$
is not upward-locally finite (thanks to the weakly elementary splittings
$\mathscr {X}_Z$
is not upward-locally finite (thanks to the weakly elementary splittings
![]() $\wedge (a^k,1)$
for arbitrary
$\wedge (a^k,1)$
for arbitrary
![]() $k\in \mathbb {Z}$
), a polysimplex stabilizer need not have finite index in a vertex stabilizer, so we need to be more careful now. Let
$k\in \mathbb {Z}$
), a polysimplex stabilizer need not have finite index in a vertex stabilizer, so we need to be more careful now. Let
![]() $P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
be a polysimplex. Write
$P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
be a polysimplex. Write
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
for the pointwise stabilizer of P, so
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
for the pointwise stabilizer of P, so
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
is a finite index subgroup of
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
is a finite index subgroup of
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)$
. Since the bottom vertex
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)$
. Since the bottom vertex
![]() $[\tau ]_Z$
is the only vertex of P with m feet, any element stabilizing P must fix
$[\tau ]_Z$
is the only vertex of P with m feet, any element stabilizing P must fix
![]() $[\tau ]_Z$
. Thus, we have inclusions
$[\tau ]_Z$
. Thus, we have inclusions
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)\le \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)\le \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
.
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)\le \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)\le \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
.
Note that
![]() $B_m\wr Z\cong \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
, and analogously to the argument in Section 4.1, this isomorphism can be realized as
$B_m\wr Z\cong \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
, and analogously to the argument in Section 4.1, this isomorphism can be realized as
If
![]() $\beta $
is pure, then for any
$\beta $
is pure, then for any
![]() $\Delta _i\in S_i$
, we have
$\Delta _i\in S_i$
, we have
![]() $[1,\beta ,1](\Delta _1\oplus \cdots \oplus \Delta _m)_Z = (\Delta _1\oplus \cdots \oplus \Delta _m)_Z$
. Hence, the restriction of
$[1,\beta ,1](\Delta _1\oplus \cdots \oplus \Delta _m)_Z = (\Delta _1\oplus \cdots \oplus \Delta _m)_Z$
. Hence, the restriction of
![]() $\eta $
to
$\eta $
to
![]() $PB_m$
lands in
$PB_m$
lands in
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
. The standard projection
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
. The standard projection
![]() $B_m\wr Z \to B_m$
induces, via
$B_m\wr Z \to B_m$
induces, via
![]() $\eta $
, an epimorphism
$\eta $
, an epimorphism
![]() $\theta \, {\colon}\, \operatorname{\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)\to B_m$
. We have shown that the image of
$\theta \, {\colon}\, \operatorname{\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)\to B_m$
. We have shown that the image of
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
under
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
under
![]() $\theta $
contains
$\theta $
contains
![]() $PB_m$
, and so has finite index in
$PB_m$
, and so has finite index in
![]() $B_m$
. The kernel of
$B_m$
. The kernel of
![]() $\theta $
is isomorphic to
$\theta $
is isomorphic to
![]() $Z^m$
. Since any finite index subgroup of
$Z^m$
. Since any finite index subgroup of
![]() $B_m$
is of type
$B_m$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
, and since any subgroup of
$\operatorname {\mathrm {F}}_\infty $
, and since any subgroup of
![]() $Z^m$
is finitely generated free abelian, hence type
$Z^m$
is finitely generated free abelian, hence type
![]() $\operatorname {\mathrm {F}}_\infty $
, we conclude that
$\operatorname {\mathrm {F}}_\infty $
, we conclude that
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
is of type
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
, being an extension of a type
$\operatorname {\mathrm {F}}_\infty $
, being an extension of a type
![]() $\operatorname {\mathrm {F}}_\infty $
group by a type
$\operatorname {\mathrm {F}}_\infty $
group by a type
![]() $\operatorname {\mathrm {F}}_\infty $
group. Since
$\operatorname {\mathrm {F}}_\infty $
group. Since
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
has finite index in
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}^0(P)$
has finite index in
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)$
, we are done.
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}(P)$
, we are done.
The failure of
![]() $\mathscr {X}_Z$
to be upward-locally finite not only makes the stabilizer argument harder, but also makes the cocompactness argument harder. Let
$\mathscr {X}_Z$
to be upward-locally finite not only makes the stabilizer argument harder, but also makes the cocompactness argument harder. Let
![]() $\mathscr {X}_Z^{h\le m}$
be the full subcomplex of
$\mathscr {X}_Z^{h\le m}$
be the full subcomplex of
![]() $\mathscr {X}_Z$
spanned by all vertices with at most m feet.
$\mathscr {X}_Z$
spanned by all vertices with at most m feet.
Lemma 5.7 For each
![]() $m\in \mathbb {N}$
, the sublevel complex
$m\in \mathbb {N}$
, the sublevel complex
![]() $\mathscr {X}_Z^{h\le m}$
is cocompact under the action of
$\mathscr {X}_Z^{h\le m}$
is cocompact under the action of
![]() $\operatorname {br}\!R$
.
$\operatorname {br}\!R$
.
Proof By the same argument as in Section 4.1 for
![]() $\mathscr {X}_d(G_*)$
, the action is transitive on vertices with a given number of feet, so in
$\mathscr {X}_d(G_*)$
, the action is transitive on vertices with a given number of feet, so in
![]() $\mathscr {X}_Z^{h\le m}$
there are finitely many (in fact exactly m) vertex orbits. However, since we no longer have upward-local finiteness, we need to do more work to see that there are finitely many polysimplex orbits. It suffices to prove that for any vertex
$\mathscr {X}_Z^{h\le m}$
there are finitely many (in fact exactly m) vertex orbits. However, since we no longer have upward-local finiteness, we need to do more work to see that there are finitely many polysimplex orbits. It suffices to prove that for any vertex
![]() $[\tau ]_Z$
, there are finitely many
$[\tau ]_Z$
, there are finitely many
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
-orbits of polysimplices with
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
-orbits of polysimplices with
![]() $[\tau ]_Z$
as their bottom vertex. Let
$[\tau ]_Z$
as their bottom vertex. Let
![]() $P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
be a polysimplex with
$P=\operatorname {\mathrm {poly}}([\tau ];S_1,\dots ,S_m)$
be a polysimplex with
![]() $[\tau ]_Z$
as its bottom vertex. As in the proof of Lemma 5.6, we have
$[\tau ]_Z$
as its bottom vertex. As in the proof of Lemma 5.6, we have
![]() $B_m\wr Z\cong \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
via the isomorphism
$B_m\wr Z\cong \operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
via the isomorphism
Note that for any
![]() $k\in \mathbb {Z}$
, we have
$k\in \mathbb {Z}$
, we have
 $$ \begin{align*} [1,b^{-k},1][\wedge,(a^k,1),1]_Z & =[\wedge,(a^{-k},c^{-k}),\wedge][\wedge,(a^k,1),1]_Z\\ &=[\wedge,(a^{-k},c^{-k})(a^k,1),1]_Z\\ &=[\wedge,(1,c^{-k}),1]_Z\\ &=[\wedge,(1,1),1]_Z\text{.} \end{align*} $$
$$ \begin{align*} [1,b^{-k},1][\wedge,(a^k,1),1]_Z & =[\wedge,(a^{-k},c^{-k}),\wedge][\wedge,(a^k,1),1]_Z\\ &=[\wedge,(a^{-k},c^{-k})(a^k,1),1]_Z\\ &=[\wedge,(1,c^{-k}),1]_Z\\ &=[\wedge,(1,1),1]_Z\text{.} \end{align*} $$
Moreover,
 $$ \begin{align*} [1,b^{-k},1][\wedge^2,1,1]_Z &=[\wedge^2,(\zeta^{-k}(1,1),c^{-k}),\wedge^2][\wedge^2,1,1]_Z\\ &=[\wedge^2,(\zeta^{-k}(1,1),c^{-k}),1]_Z\\ &=[\wedge^2,1,1]_Z\text{.} \end{align*} $$
$$ \begin{align*} [1,b^{-k},1][\wedge^2,1,1]_Z &=[\wedge^2,(\zeta^{-k}(1,1),c^{-k}),\wedge^2][\wedge^2,1,1]_Z\\ &=[\wedge^2,(\zeta^{-k}(1,1),c^{-k}),1]_Z\\ &=[\wedge^2,1,1]_Z\text{.} \end{align*} $$
(Recall that
![]() $\zeta $
is our chosen generator of
$\zeta $
is our chosen generator of
![]() $B_2\cong \mathbb {Z}$
, with
$B_2\cong \mathbb {Z}$
, with
![]() $a=\zeta (1,1)$
.) Define the signature
$a=\zeta (1,1)$
.) Define the signature
![]() $||S_i||$
of
$||S_i||$
of
![]() $S_i$
to be
$S_i$
to be
![]() $1$
if
$1$
if
![]() $S_i=\{1\}$
,
$S_i=\{1\}$
,
![]() $2$
if
$2$
if
![]() $S_i=\{1,\wedge (a^k,1)\}$
for some
$S_i=\{1,\wedge (a^k,1)\}$
for some
![]() $k\in \mathbb {Z}$
,
$k\in \mathbb {Z}$
,
![]() $3$
if
$3$
if
![]() $S_i=\{1,\wedge ^2\}$
, and
$S_i=\{1,\wedge ^2\}$
, and
![]() $4$
if
$4$
if
![]() $S_i=\{1,\wedge (a^k,1),\wedge ^2\}$
for some
$S_i=\{1,\wedge (a^k,1),\wedge ^2\}$
for some
![]() $k\in \mathbb {Z}$
. Extrapolating using direct sums, the above calculations show that the
$k\in \mathbb {Z}$
. Extrapolating using direct sums, the above calculations show that the
![]() $\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
-orbit of P includes every
$\operatorname {\mathrm {Stab}}_{\operatorname {br}\!R}([\tau ]_Z)$
-orbit of P includes every
![]() $\operatorname {\mathrm {poly}}([\tau ];T_1,\dots ,T_m)$
with
$\operatorname {\mathrm {poly}}([\tau ];T_1,\dots ,T_m)$
with
![]() $||T_i||=||S_i||$
for each
$||T_i||=||S_i||$
for each
![]() $1\le i\le m$
. Since there are only finitely many (four) possibilities for each
$1\le i\le m$
. Since there are only finitely many (four) possibilities for each
![]() $||S_i||$
, we are done.
$||S_i||$
, we are done.
Combining Proposition 5.4 and Lemmas 5.6 and 5.7, we get the following.
Corollary 5.8 The group
![]() $\operatorname {br}\!R$
acts on the contractible complex
$\operatorname {br}\!R$
acts on the contractible complex
![]() $\mathscr {X}_Z$
with cell stabilizers of type
$\mathscr {X}_Z$
with cell stabilizers of type
![]() $\operatorname {\mathrm {F}}_\infty $
, and with cocompact sublevel complexes
$\operatorname {\mathrm {F}}_\infty $
, and with cocompact sublevel complexes
![]() $\mathscr {X}_Z^{h\le m}$
.
$\mathscr {X}_Z^{h\le m}$
.
5.2 Descending links
By Citation 4.4 and Corollary 5.8, to get
![]() $\operatorname {br}\!R$
to be of type
$\operatorname {br}\!R$
to be of type
![]() $\operatorname {\mathrm {F}}_\infty $
, it remains to prove that descending links get arbitrarily highly connected. (Note that h is affine on polysimplices, so it really is a Morse function.) Much of the work in this subsection will be inspired by [Reference Brady, Burillo, Cleary and SteinBM16, Section 6] and [Reference SteinSZ21, Section 4.3].
$\operatorname {\mathrm {F}}_\infty $
, it remains to prove that descending links get arbitrarily highly connected. (Note that h is affine on polysimplices, so it really is a Morse function.) Much of the work in this subsection will be inspired by [Reference Brady, Burillo, Cleary and SteinBM16, Section 6] and [Reference SteinSZ21, Section 4.3].
Since
![]() $\mathscr {X}_Z$
is a polysimplicial complex, the link of a vertex v is a simplicial complex, with a k-simplex for each
$\mathscr {X}_Z$
is a polysimplicial complex, the link of a vertex v is a simplicial complex, with a k-simplex for each
![]() $(k+1)$
-dimensional polysimplex containing v. If the polysimplex achieves its maximum h value at v, then the corresponding simplex in the link of v is even in the descending link. Note that vertices with the same number of feet have isomorphic descending links, so just like the complexes
$(k+1)$
-dimensional polysimplex containing v. If the polysimplex achieves its maximum h value at v, then the corresponding simplex in the link of v is even in the descending link. Note that vertices with the same number of feet have isomorphic descending links, so just like the complexes
![]() $\mathscr {L}_d^m(B_*\wr G)$
from Section 4.3, we can denote by
$\mathscr {L}_d^m(B_*\wr G)$
from Section 4.3, we can denote by
![]() $\mathscr {L}^m_Z$
the simplicial complex that is isomorphic to the descending link of any vertex with m feet.
$\mathscr {L}^m_Z$
the simplicial complex that is isomorphic to the descending link of any vertex with m feet.
Definition 5.6 (Merging)
Call an element
![]() $\Upsilon $
of
$\Upsilon $
of
![]() $\mathscr {G}$
a merging if
$\mathscr {G}$
a merging if
![]() $\Upsilon ^{-1}$
is a splitting. Call it simple or weakly elementary if its inverse is, as a splitting. If
$\Upsilon ^{-1}$
is a splitting. Call it simple or weakly elementary if its inverse is, as a splitting. If
![]() $v=[\tau ]_Z$
is a vertex in
$v=[\tau ]_Z$
is a vertex in
![]() $\mathscr {X}_Z$
and
$\mathscr {X}_Z$
and
![]() $\Upsilon $
is a merging such that the product
$\Upsilon $
is a merging such that the product
![]() $[\tau ]\Upsilon $
makes sense, then we call
$[\tau ]\Upsilon $
makes sense, then we call
![]() $[\tau ]\Upsilon _Z$
a merging of v.
$[\tau ]\Upsilon _Z$
a merging of v.
For
![]() $\Upsilon $
a merging, write
$\Upsilon $
a merging, write
![]() $\Upsilon ^{(i)}$
for the merging
$\Upsilon ^{(i)}$
for the merging
![]() $1\oplus \cdots \oplus 1\oplus \Upsilon \oplus 1\oplus \cdots \oplus 1$
, where
$1\oplus \cdots \oplus 1\oplus \Upsilon \oplus 1\oplus \cdots \oplus 1$
, where
![]() $\Upsilon $
is the ith direct summand. We see that the vertices of the descending link
$\Upsilon $
is the ith direct summand. We see that the vertices of the descending link
![]() $\operatorname {lk}^\downarrow \! v$
of v are precisely the nontrivial, weakly elementary, simple mergings of v. Writing
$\operatorname {lk}^\downarrow \! v$
of v are precisely the nontrivial, weakly elementary, simple mergings of v. Writing
![]() , this means that to obtain a vertex of
, this means that to obtain a vertex of
![]() $\operatorname {lk}^\downarrow \! v$
, we choose a representative
$\operatorname {lk}^\downarrow \! v$
, we choose a representative
![]() $[\tau ]$
of
$[\tau ]$
of
![]() $v=[\tau ]_Z$
, take
$v=[\tau ]_Z$
, take
![]() $\Upsilon $
to be either
$\Upsilon $
to be either
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
or
$k\in \mathbb {Z}$
or
![]() $\vee ^2$
, and then take
$\vee ^2$
, and then take
![]() $[\tau ]\Upsilon ^{(i)}_Z$
for some i. If we already have a fixed representative
$[\tau ]\Upsilon ^{(i)}_Z$
for some i. If we already have a fixed representative
![]() $[\tau ]$
of v, then in addition to all of the above, we first multiply
$[\tau ]$
of v, then in addition to all of the above, we first multiply
![]() $[\tau ]$
on the right by an element of
$[\tau ]$
on the right by an element of
![]() $B_m\wr Z$
, where
$B_m\wr Z$
, where
![]() $m=h(v)$
(to account for potentially changing representatives). In all that follows, we will often identify
$m=h(v)$
(to account for potentially changing representatives). In all that follows, we will often identify
![]() $B_m\wr Z$
with its image in
$B_m\wr Z$
with its image in
![]() $\mathscr {G}$
under
$\mathscr {G}$
under
![]() $g\mapsto [1,g,1]$
.
$g\mapsto [1,g,1]$
.
We can denote vertices of
![]() $\mathscr {L}^m_Z$
by
$\mathscr {L}^m_Z$
by
![]() $g\Upsilon ^{(i)}_Z$
for
$g\Upsilon ^{(i)}_Z$
for
![]() $g\in B_m\wr Z$
,
$g\in B_m\wr Z$
,
![]() $\Upsilon $
equal to either
$\Upsilon $
equal to either
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
or
$k\in \mathbb {Z}$
or
![]() $\vee ^2$
, and i some appropriate number. If
$\vee ^2$
, and i some appropriate number. If
![]() $\mathscr {L}^m_Z$
is representing
$\mathscr {L}^m_Z$
is representing
![]() $\operatorname {lk}^\downarrow \! [\tau ]_Z$
, then
$\operatorname {lk}^\downarrow \! [\tau ]_Z$
, then
![]() $g\Upsilon ^{(i)}_Z$
represents
$g\Upsilon ^{(i)}_Z$
represents
![]() $[\tau ]g\Upsilon ^{(i)}_Z$
.
$[\tau ]g\Upsilon ^{(i)}_Z$
.
Definition 5.7 (Type, mass)
Let
![]() $[\tau ]_Z$
be a vertex of
$[\tau ]_Z$
be a vertex of
![]() $\mathscr {X}_Z$
with
$\mathscr {X}_Z$
with
![]() $h([\tau ]_Z)=m$
. Consider a vertex of
$h([\tau ]_Z)=m$
. Consider a vertex of
![]() $\operatorname {lk}^\downarrow \! [\tau ]_Z$
, which is a nontrivial, weakly elementary, simple merging of
$\operatorname {lk}^\downarrow \! [\tau ]_Z$
, which is a nontrivial, weakly elementary, simple merging of
![]() $[\tau ]_Z$
, so one of the form
$[\tau ]_Z$
, so one of the form
![]() $[\tau ]g\Upsilon ^{(i)}_Z$
, for
$[\tau ]g\Upsilon ^{(i)}_Z$
, for
![]() $g=\beta (z_1,\dots ,z_m)\in B_m\wr Z$
,
$g=\beta (z_1,\dots ,z_m)\in B_m\wr Z$
,
![]() $\Upsilon $
of the form
$\Upsilon $
of the form
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
or
$k\in \mathbb {Z}$
or
![]() $\vee ^2$
, and some i. Define the type of this merging to be
$\vee ^2$
, and some i. Define the type of this merging to be
![]() $\Upsilon $
, so the type is either
$\Upsilon $
, so the type is either
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
or
$k\in \mathbb {Z}$
or
![]() $\vee ^2$
. Define the mass of this merging to be
$\vee ^2$
. Define the mass of this merging to be
![]() $2$
if it is of type
$2$
if it is of type
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
, and
$k\in \mathbb {Z}$
, and
![]() $3$
if it is of type
$3$
if it is of type
![]() $\vee ^2$
(so the mass is the “number of feet” that
$\vee ^2$
(so the mass is the “number of feet” that
![]() $\Upsilon $
is merging together).
$\Upsilon $
is merging together).
In order to understand
![]() $\mathscr {L}^m_Z$
, we will map it to a certain complex of disks, defined as follows.
$\mathscr {L}^m_Z$
, we will map it to a certain complex of disks, defined as follows.
Definition 5.8 (
 $(2,5/2)$
-disk complex)
$(2,5/2)$
-disk complex)
Let
![]() $\mathcal {S}_{b,m}^g$
be a surface with b boundary components, m marked points, and genus g. The
$\mathcal {S}_{b,m}^g$
be a surface with b boundary components, m marked points, and genus g. The
![]() $(2,5/2)$
-marked-point-disk complex
$(2,5/2)$
-marked-point-disk complex
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is the simplicial complex defined as follows. A vertex is an isotopy class of an embedded disk enclosing precisely two marked points in its interior and either
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is the simplicial complex defined as follows. A vertex is an isotopy class of an embedded disk enclosing precisely two marked points in its interior and either
![]() $0$
or
$0$
or
![]() $1$
marked points in its boundary. If a disk has zero marked points in its boundary, call it a
$1$
marked points in its boundary. If a disk has zero marked points in its boundary, call it a
![]() $2$
-disk, and if it has one marked point in its boundary, call it a
$2$
-disk, and if it has one marked point in its boundary, call it a
![]() $5/2$
-disk (two points inside plus one point “halfway inside” equals two and a half points inside, hence the name
$5/2$
-disk (two points inside plus one point “halfway inside” equals two and a half points inside, hence the name
![]() $5/2$
-disk). A k-simplex in
$5/2$
-disk). A k-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is an isotopy class of
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is an isotopy class of
![]() $k+1$
(pairwise nonisotopic) embedded disks such that each one is either a
$k+1$
(pairwise nonisotopic) embedded disks such that each one is either a
![]() $2$
-disk or a
$2$
-disk or a
![]() $5/2$
-disk, and any two of them are either disjoint or nested. The face relation is given by taking subsets.
$5/2$
-disk, and any two of them are either disjoint or nested. The face relation is given by taking subsets.
Here, when we call two isotopy classes “disjoint” or “nested,” we of course mean that they admit disjoint or nested representatives. If one disk is nested in a (nonisotopic) second disk, then necessarily the former is a
![]() $2$
-disk and the latter is a
$2$
-disk and the latter is a
![]() $5/2$
-disk. Similar to how the usual disk complex can be viewed as a subcomplex of the curve complex (outside some pathological cases), this
$5/2$
-disk. Similar to how the usual disk complex can be viewed as a subcomplex of the curve complex (outside some pathological cases), this
![]() $(2,5/2)$
-marked-point-disk complex can usually be viewed as a subcomplex of the arc-and-curve complex: the boundary of a
$(2,5/2)$
-marked-point-disk complex can usually be viewed as a subcomplex of the arc-and-curve complex: the boundary of a
![]() $2$
-disk is a curve and the boundary of a
$2$
-disk is a curve and the boundary of a
![]() $5/2$
-disk is an arc. See Figure 7 for example. (The astute reader may wonder why we are using
$5/2$
-disk is an arc. See Figure 7 for example. (The astute reader may wonder why we are using
![]() $5/2$
-disks instead of
$5/2$
-disks instead of
![]() $3$
-disks; the answer is that the analog of Proposition 5.11 would not hold if we used
$3$
-disks; the answer is that the analog of Proposition 5.11 would not hold if we used
![]() $3$
-disks.)
$3$
-disks.)

Figure 7: An example of a
![]() $1$
-simplex in
$1$
-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{1,5}^0)$
. The disk bounded in red is a
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{1,5}^0)$
. The disk bounded in red is a
![]() $2$
-disk, the disk bounded in blue is a
$2$
-disk, the disk bounded in blue is a
![]() $5/2$
-disk, and they are nested.
$5/2$
-disk, and they are nested.
Now let us map
![]() $\mathscr {L}^m_Z$
to
$\mathscr {L}^m_Z$
to
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
, where
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
, where
![]() $\mathcal {S}_m=\mathcal {S}_{1,m}^0$
. To start, we will just define the map on the vertices. A vertex of
$\mathcal {S}_m=\mathcal {S}_{1,m}^0$
. To start, we will just define the map on the vertices. A vertex of
![]() $\mathscr {L}^m_Z$
is of the form
$\mathscr {L}^m_Z$
is of the form
![]() $\beta (z_1,\dots ,z_m)\Upsilon ^{(i)}_Z$
, where
$\beta (z_1,\dots ,z_m)\Upsilon ^{(i)}_Z$
, where
![]() $\beta (z_1,\dots ,z_m)\in B_m\wr Z$
,
$\beta (z_1,\dots ,z_m)\in B_m\wr Z$
,
![]() $\Upsilon $
is of the form
$\Upsilon $
is of the form
![]() $(a^k,1)\vee $
for some
$(a^k,1)\vee $
for some
![]() $k\in \mathbb {Z}$
or
$k\in \mathbb {Z}$
or
![]() $\vee ^2$
, and i is some number. Define
$\vee ^2$
, and i is some number. Define
as follows. If
![]() $\Upsilon =(a^k,1)\vee $
for some k, then define
$\Upsilon =(a^k,1)\vee $
for some k, then define
![]() $D(\Upsilon ^{(i)})$
to be a
$D(\Upsilon ^{(i)})$
to be a
![]() $2$
-disk that is a tubular neighborhood of the
$2$
-disk that is a tubular neighborhood of the
![]() $2$
-matching
$2$
-matching
![]() $\{i,i+1\}$
(recall from before that we fix an embedding of the linear graph into the surface, and so matchings make sense). If
$\{i,i+1\}$
(recall from before that we fix an embedding of the linear graph into the surface, and so matchings make sense). If
![]() $\Upsilon =\vee ^2$
, then define
$\Upsilon =\vee ^2$
, then define
![]() $D(\Upsilon ^{(i)})$
to be a
$D(\Upsilon ^{(i)})$
to be a
![]() $5/2$
-disk that is obtained by taking a tubular neighborhood of the subset obtained from the
$5/2$
-disk that is obtained by taking a tubular neighborhood of the subset obtained from the
![]() $3$
-matching
$3$
-matching
![]() $\{i,i+1,i+2\}$
by removing a small disk centered at
$\{i,i+1,i+2\}$
by removing a small disk centered at
![]() $i+2$
, in such a way that
$i+2$
, in such a way that
![]() $i+2$
lies precisely on the boundary of the neighborhood. For example, in Figure 7, if we label the marked points
$i+2$
lies precisely on the boundary of the neighborhood. For example, in Figure 7, if we label the marked points
![]() $1$
–
$1$
–
![]() $5$
from left to right, then (up to isotopy) the disk bounded in blue is
$5$
from left to right, then (up to isotopy) the disk bounded in blue is
![]() $D\left ((\vee ^2)^{(2)}\right )$
. Now define
$D\left ((\vee ^2)^{(2)}\right )$
. Now define
![]() $\mu $
via
$\mu $
via
Lemma 5.9 The map
![]() $\mu $
is well defined on vertices.
$\mu $
is well defined on vertices.
Proof The proof is similar to that of Lemma 4.7. Let
![]() $\gamma (y_1,\dots ,y_q)\in B_q\wr Z$
for appropriate q, so
$\gamma (y_1,\dots ,y_q)\in B_q\wr Z$
for appropriate q, so
Let
![]() $\gamma '(y_1',\dots ,y_m')\in B_m\wr \operatorname {\mathrm {brGrig}}$
and
$\gamma '(y_1',\dots ,y_m')\in B_m\wr \operatorname {\mathrm {brGrig}}$
and
![]() $i'$
be such that
$i'$
be such that
Note that the
![]() $y_j'$
might not lie in Z, but the only way this could happen is when
$y_j'$
might not lie in Z, but the only way this could happen is when
![]() $j=i'$
, and then only if
$j=i'$
, and then only if
![]() $\Upsilon $
has mass
$\Upsilon $
has mass
![]() $2$
, so
$2$
, so
![]() $y^{\prime }_{i'}$
is a power of a. In this case, we can let
$y^{\prime }_{i'}$
is a power of a. In this case, we can let
![]() $\Upsilon '$
be
$\Upsilon '$
be
![]() $\Upsilon =(a^k,1)\vee $
with k changed appropriately, and (changing the definition of
$\Upsilon =(a^k,1)\vee $
with k changed appropriately, and (changing the definition of
![]() $y^{\prime }_{i'}$
) get
$y^{\prime }_{i'}$
) get
with all
![]() $y_j'$
in Z. Now we have
$y_j'$
in Z. Now we have
for some
![]() $z_i'\in Z$
. Since all the
$z_i'\in Z$
. Since all the
![]() $z_j$
and
$z_j$
and
![]() $y_j'$
are in Z, this maps under
$y_j'$
are in Z, this maps under
![]() $\mu $
to
$\mu $
to
![]() $(D((\Upsilon ')^{(i')}))(\beta \gamma ')^{-1}$
. We need to show that this equals
$(D((\Upsilon ')^{(i')}))(\beta \gamma ')^{-1}$
. We need to show that this equals
![]() $(D(\Upsilon ^{(i)}))\beta ^{-1}$
, or equivalently that
$(D(\Upsilon ^{(i)}))\beta ^{-1}$
, or equivalently that
![]() $(D(\Upsilon ^{(i)}))\gamma ' = D((\Upsilon ')^{(i')})$
. If
$(D(\Upsilon ^{(i)}))\gamma ' = D((\Upsilon ')^{(i')})$
. If
![]() $\Upsilon $
(and hence
$\Upsilon $
(and hence
![]() $\Upsilon '$
) has mass
$\Upsilon '$
) has mass
![]() $2$
, then this follows by the same argument as in the proof of Lemma 4.7. Now suppose
$2$
, then this follows by the same argument as in the proof of Lemma 4.7. Now suppose
![]() $\Upsilon =\Upsilon '=\vee ^2$
. Then
$\Upsilon =\Upsilon '=\vee ^2$
. Then
![]() $\gamma '$
is obtained from
$\gamma '$
is obtained from
![]() $\gamma $
by replacing the ith strand (counting from the top) with three parallel strands—call this intermediate braid
$\gamma $
by replacing the ith strand (counting from the top) with three parallel strands—call this intermediate braid
![]() $\gamma "$
—and possibly braiding the first two of these around each other some number of times (depending on the braided wreath recursion of
$\gamma "$
—and possibly braiding the first two of these around each other some number of times (depending on the braided wreath recursion of
![]() $y_{i'}$
, which has some power of a in its left entry and some element of Z in its right entry). When acting on
$y_{i'}$
, which has some power of a in its left entry and some element of Z in its right entry). When acting on
![]() $D(\Upsilon ^{(i)})$
, this braiding of the first two strands does not affect the (equivalence class of the)
$D(\Upsilon ^{(i)})$
, this braiding of the first two strands does not affect the (equivalence class of the)
![]() $5/2$
-disk, so
$5/2$
-disk, so
![]() $(D(\Upsilon ^{(i)}))\gamma ' = (D(\Upsilon ^{(i)}))\gamma "$
. It is clear that
$(D(\Upsilon ^{(i)}))\gamma ' = (D(\Upsilon ^{(i)}))\gamma "$
. It is clear that
![]() $(D(\Upsilon ^{(i)}))\gamma " = D((\Upsilon ')^{(i')})$
, so we are done.
$(D(\Upsilon ^{(i)}))\gamma " = D((\Upsilon ')^{(i')})$
, so we are done.
Now we want to extend
![]() $\mu $
to all simplices of
$\mu $
to all simplices of
![]() $\mathscr {L}^m_Z$
. We need to show that if vertices
$\mathscr {L}^m_Z$
. We need to show that if vertices
![]() $w_0,\dots ,w_k$
span a simplex in
$w_0,\dots ,w_k$
span a simplex in
![]() $\mathscr {L}^m_Z$
, then their images under
$\mathscr {L}^m_Z$
, then their images under
![]() $\mu $
span a simplex in
$\mu $
span a simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
. Since
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
. Since
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
is a flag complex by construction, it suffices to do this for
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
is a flag complex by construction, it suffices to do this for
![]() $k=1$
, i.e., to show the following.
$k=1$
, i.e., to show the following.
Lemma 5.10 (Extends to simplices)
If two vertices w and u span an edge in
![]() $\mathscr {L}^m_Z$
, then their images under
$\mathscr {L}^m_Z$
, then their images under
![]() $\mu $
span an edge in
$\mu $
span an edge in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
.
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
.
Proof View
![]() $\mathscr {L}^m_Z$
as
$\mathscr {L}^m_Z$
as
![]() $\operatorname {lk}^\downarrow \! v$
for some vertex
$\operatorname {lk}^\downarrow \! v$
for some vertex
![]() $v=[\tau ]_Z$
of
$v=[\tau ]_Z$
of
![]() $\mathscr {X}_Z$
with
$\mathscr {X}_Z$
with
![]() $h(v)=m$
, so w and u are adjacent vertices to v with
$h(v)=m$
, so w and u are adjacent vertices to v with
![]() $h(w),h(u)<m$
. The fact that w and u span an edge in
$h(w),h(u)<m$
. The fact that w and u span an edge in
![]() $\operatorname {lk}^\downarrow \! v$
means that there is a two-dimensional polysimplex, i.e., a square or a triangle, in
$\operatorname {lk}^\downarrow \! v$
means that there is a two-dimensional polysimplex, i.e., a square or a triangle, in
![]() $\mathscr {X}_Z$
containing v, w, and u. First, suppose that it is a square. Then there is a merging of v of the form
$\mathscr {X}_Z$
containing v, w, and u. First, suppose that it is a square. Then there is a merging of v of the form
![]() $[\tau ]\beta (z_1,\dots ,z_m)\Upsilon _Z$
for
$[\tau ]\beta (z_1,\dots ,z_m)\Upsilon _Z$
for
![]() $\beta (z_1,\dots ,z_m)\in B_m\wr Z$
and
$\beta (z_1,\dots ,z_m)\in B_m\wr Z$
and
say with
![]() $\Upsilon _1$
in the
$\Upsilon _1$
in the
![]() $i_1$
th spot and
$i_1$
th spot and
![]() $\Upsilon _2$
in the
$\Upsilon _2$
in the
![]() $i_2$
th spot, such that the following holds: if
$i_2$
th spot, such that the following holds: if
![]() $\Psi _i$
is
$\Psi _i$
is
![]() $\Upsilon $
with
$\Upsilon $
with
![]() $\Upsilon _i$
replaced by an appropriate number of copies of
$\Upsilon _i$
replaced by an appropriate number of copies of
![]() $1$
, then
$1$
, then
![]() $w=[\tau ]\beta (z_1,\dots ,z_m)(\Psi _1)_Z$
and
$w=[\tau ]\beta (z_1,\dots ,z_m)(\Psi _1)_Z$
and
![]() $u=[\tau ]\beta (z_1,\dots ,z_m)(\Psi _2)_Z$
. Clearly,
$u=[\tau ]\beta (z_1,\dots ,z_m)(\Psi _2)_Z$
. Clearly,
![]() $D(\Psi _1)$
and
$D(\Psi _1)$
and
![]() $D(\Psi _2)$
are disjoint; hence so are
$D(\Psi _2)$
are disjoint; hence so are
![]() $\mu (w)=(D(\Psi _1))\beta ^{-1}$
and
$\mu (w)=(D(\Psi _1))\beta ^{-1}$
and
![]() $\mu (u)=(D(\Psi _2))\beta ^{-1}$
. Now suppose that the two-dimensional polysimplex containing v, w, and u is a triangle. This means that there we can choose
$\mu (u)=(D(\Psi _2))\beta ^{-1}$
. Now suppose that the two-dimensional polysimplex containing v, w, and u is a triangle. This means that there we can choose
![]() $[\tau ']$
, k, and i such that v, w, and u are the vertices of the polysimplex
$[\tau ']$
, k, and i such that v, w, and u are the vertices of the polysimplex
![]() $\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_{m-2})$
, where
$\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_{m-2})$
, where
![]() $S_j=\{1\}$
for all
$S_j=\{1\}$
for all
![]() $j\ne i$
and
$j\ne i$
and
![]() $S_i=\{1,\wedge (a^k,1),\wedge ^2\}$
. Say w has mass
$S_i=\{1,\wedge (a^k,1),\wedge ^2\}$
. Say w has mass
![]() $3$
relative to v (and u has mass
$3$
relative to v (and u has mass
![]() $2$
), so
$2$
), so
![]() $w=[\tau ']_Z$
,
$w=[\tau ']_Z$
,
![]() $u=[\tau '](\wedge (a^k,1))^{(i)}_Z$
, and
$u=[\tau '](\wedge (a^k,1))^{(i)}_Z$
, and
![]() $v=[\tau '](\wedge ^2)^{(i)}_Z$
. Without loss of generality,
$v=[\tau '](\wedge ^2)^{(i)}_Z$
. Without loss of generality,
![]() $[\tau ]=[\tau '](\wedge ^2)^{(i)}$
, so
$[\tau ]=[\tau '](\wedge ^2)^{(i)}$
, so
![]() $u=[\tau ](\vee a^k)^{(i)}_Z=[\tau ](\zeta ^k \vee )^{(i)}_Z$
and
$u=[\tau ](\vee a^k)^{(i)}_Z=[\tau ](\zeta ^k \vee )^{(i)}_Z$
and
![]() $w=[\tau ](\vee ^2)^{(i)}_Z$
. Now
$w=[\tau ](\vee ^2)^{(i)}_Z$
. Now
![]() $\mu (u)=\left (D(\vee ^{(i)})\right )\left ((\zeta ^k)^{(i)}\right )^{-1}=D(\vee ^{(i)})$
and
$\mu (u)=\left (D(\vee ^{(i)})\right )\left ((\zeta ^k)^{(i)}\right )^{-1}=D(\vee ^{(i)})$
and
![]() $\mu (w)=D\left ((\vee ^2)^{(i)}\right )$
, and the former is nested in the latter as desired.
$\mu (w)=D\left ((\vee ^2)^{(i)}\right )$
, and the former is nested in the latter as desired.
At this point, we have a simplicial map
Our next goal is to prove that it is a surjective complete join. It is clearly surjective on vertices, and is simplexwise injective, so it suffices to show the following.
Proposition 5.11 Let
![]() $w_0,\dots ,w_k$
be vertices of
$w_0,\dots ,w_k$
be vertices of
![]() $\mathscr {L}^m_Z$
whose images under
$\mathscr {L}^m_Z$
whose images under
![]() $\mu $
span a k-simplex in
$\mu $
span a k-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
. Then
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
. Then
![]() $w_0,\dots ,w_k$
span a k-simplex in
$w_0,\dots ,w_k$
span a k-simplex in
![]() $\mathscr {L}^m_Z$
. Hence,
$\mathscr {L}^m_Z$
. Hence,
![]() $\mu $
is a complete join.
$\mu $
is a complete join.
Proof If
![]() $k=0$
, then there is nothing to show, so assume that
$k=0$
, then there is nothing to show, so assume that
![]() $k>0$
. By induction,
$k>0$
. By induction,
![]() $w_1,\dots ,w_k$
span a simplex in
$w_1,\dots ,w_k$
span a simplex in
![]() $\mathscr {L}^m_Z$
, call it
$\mathscr {L}^m_Z$
, call it
![]() $\sigma $
. The image
$\sigma $
. The image
![]() $\mu (\sigma )$
is represented by k disks that are pairwise disjoint or nested, and such that the disk
$\mu (\sigma )$
is represented by k disks that are pairwise disjoint or nested, and such that the disk
![]() $\mu (w_0)$
is disjoint or nested with each of them. If
$\mu (w_0)$
is disjoint or nested with each of them. If
![]() $\mu (w_0)$
is disjoint from all the disks in
$\mu (w_0)$
is disjoint from all the disks in
![]() $\mu (\sigma )$
, then the argument in the proof of Proposition 4.11 shows that
$\mu (\sigma )$
, then the argument in the proof of Proposition 4.11 shows that
![]() $w_0,\dots ,w_k$
span a simplex in
$w_0,\dots ,w_k$
span a simplex in
![]() $\mathscr {L}^m_Z$
. Now assume that this is not the case, so without loss of generality
$\mathscr {L}^m_Z$
. Now assume that this is not the case, so without loss of generality
![]() $w_0$
has mass
$w_0$
has mass
![]() $2$
,
$2$
,
![]() $w_1$
has mass
$w_1$
has mass
![]() $3$
,
$3$
,
![]() $\mu (w_0)$
is nested in
$\mu (w_0)$
is nested in
![]() $\mu (w_1)$
, and both
$\mu (w_1)$
, and both
![]() $\mu (w_0)$
and
$\mu (w_0)$
and
![]() $\mu (w_1)$
are disjoint from
$\mu (w_1)$
are disjoint from
![]() $\mu (w_i)$
for all
$\mu (w_i)$
for all
![]() $2\le i\le k$
. Now view
$2\le i\le k$
. Now view
![]() $\mathscr {L}^m_Z$
as
$\mathscr {L}^m_Z$
as
![]() $\operatorname {lk}^\downarrow \! v$
for a vertex
$\operatorname {lk}^\downarrow \! v$
for a vertex
![]() $v=[\tau ]_Z$
with
$v=[\tau ]_Z$
with
![]() $h(v)=m$
, so
$h(v)=m$
, so
![]() $\sigma $
is represented by a polysimplex containing
$\sigma $
is represented by a polysimplex containing
![]() $v,w_1,\dots ,w_k$
, with v as its vertex maximizing h. Write this polysimplex as
$v,w_1,\dots ,w_k$
, with v as its vertex maximizing h. Write this polysimplex as
![]() $\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_r)$
, so
$\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_r)$
, so
![]() $v=[\tau '](\max (S_1)\oplus \cdots \oplus \max (S_r))_Z$
. We can assume that
$v=[\tau '](\max (S_1)\oplus \cdots \oplus \max (S_r))_Z$
. We can assume that
![]() $[\tau ]=[\tau '](\max (S_1)\oplus \cdots \oplus \max (S_r))$
. Without loss of generality,
$[\tau ]=[\tau '](\max (S_1)\oplus \cdots \oplus \max (S_r))$
. Without loss of generality,
![]() $S_1=\{1,\wedge ^2\}$
and
$S_1=\{1,\wedge ^2\}$
and
Now say
![]() $w_0=[\tau ]\beta (z_1,\dots ,z_m)((a^\ell ,1)\vee )^{(i)}_Z$
for some
$w_0=[\tau ]\beta (z_1,\dots ,z_m)((a^\ell ,1)\vee )^{(i)}_Z$
for some
![]() $\beta (z_1,\dots ,z_m)\in B_m\wr Z$
, some
$\beta (z_1,\dots ,z_m)\in B_m\wr Z$
, some
![]() $\ell $
, and some i. Up to
$\ell $
, and some i. Up to
![]() $\sim _Z$
, we can actually assume
$\sim _Z$
, we can actually assume
![]() $\ell =0$
, e.g., right multiply by
$\ell =0$
, e.g., right multiply by
![]() $(b^{-\ell })^{(i)}$
. Then
$(b^{-\ell })^{(i)}$
. Then
![]() $\mu (w_0)=\left (D(\vee ^{(i)})\right )\beta ^{-1}$
, and this is disjoint from
$\mu (w_0)=\left (D(\vee ^{(i)})\right )\beta ^{-1}$
, and this is disjoint from
![]() $\mu (w_2),\dots ,\mu (w_k)$
and contained in
$\mu (w_2),\dots ,\mu (w_k)$
and contained in
![]() $\mu (w_1)$
. By the above equation for
$\mu (w_1)$
. By the above equation for
![]() $w_1$
, we have
$w_1$
, we have
![]() $\mu (w_1)=D\left ((\vee ^2)^{(1)}\right )$
, so
$\mu (w_1)=D\left ((\vee ^2)^{(1)}\right )$
, so
![]() $\mu (w_0)=D\left (\vee ^{(1)}\right )$
; hence
$\mu (w_0)=D\left (\vee ^{(1)}\right )$
; hence
![]() $D\left (\vee ^{(i)}\right ) = \left (D\left (\vee ^{(1)}\right )\right )\beta $
. This shows that, in fact,
$D\left (\vee ^{(i)}\right ) = \left (D\left (\vee ^{(1)}\right )\right )\beta $
. This shows that, in fact,
![]() ${w_0=[\tau ](\zeta ^\ell \vee )^{(1)}_Z}$
for some
${w_0=[\tau ](\zeta ^\ell \vee )^{(1)}_Z}$
for some
![]() $\ell $
; hence,
$\ell $
; hence,
Since
![]() $\max (S_1)=\wedge ^2$
and
$\max (S_1)=\wedge ^2$
and
![]() $\wedge \zeta ^\ell \vee =a^\ell $
, we conclude that
$\wedge \zeta ^\ell \vee =a^\ell $
, we conclude that
Now setting
![]() $S_1'=\{1,\wedge (a^\ell ,1),\wedge ^2\}$
, we see that the polysimplex
$S_1'=\{1,\wedge (a^\ell ,1),\wedge ^2\}$
, we see that the polysimplex
![]() $\operatorname {\mathrm {poly}}([\tau '];S_1',S_2,\dots ,S_r)$
contains
$\operatorname {\mathrm {poly}}([\tau '];S_1',S_2,\dots ,S_r)$
contains
![]() $w_0$
. Since it has
$w_0$
. Since it has
![]() $\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_r)$
as a face, it also contains
$\operatorname {\mathrm {poly}}([\tau '];S_1,\dots ,S_r)$
as a face, it also contains
![]() $v,w_1,\dots ,w_k$
, so we conclude that
$v,w_1,\dots ,w_k$
, so we conclude that
![]() $w_0,\dots ,w_k$
span a simplex in
$w_0,\dots ,w_k$
span a simplex in
![]() $\operatorname {lk}^\downarrow \! v$
.
$\operatorname {lk}^\downarrow \! v$
.
Now that we know
![]() $\mu $
is a complete join, we can understand higher connectivity of
$\mu $
is a complete join, we can understand higher connectivity of
![]() $\mathscr {L}^m_Z$
by analyzing higher connectivity of
$\mathscr {L}^m_Z$
by analyzing higher connectivity of
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
.
${\mathbb {D}}_{2,5/2}(\mathcal {S}_m)$
.
Proposition 5.12 The complex
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
![]() $\lfloor \frac {m+1}{3}\rfloor -1$
.
$\lfloor \frac {m+1}{3}\rfloor -1$
.
Proof First, we show that
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is homotopy equivalent to
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is homotopy equivalent to
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
. Given a k-simplex
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
. Given a k-simplex
![]() $\sigma =\{D_0,\dots ,D_k\}$
in
$\sigma =\{D_0,\dots ,D_k\}$
in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
, let
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
, let
![]() $n_{5/2}(\sigma )$
be the number of
$n_{5/2}(\sigma )$
be the number of
![]() $D_i$
’s that are
$D_i$
’s that are
![]() $5/2$
-disks. Define a Morse function on the barycentric subdivision
$5/2$
-disks. Define a Morse function on the barycentric subdivision
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)'$
by sending a k-simplex
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)'$
by sending a k-simplex
![]() $\sigma $
to the ordered pair
$\sigma $
to the ordered pair
![]() $(n_{5/2}(\sigma ),-\dim (\sigma ))$
. This takes on finitely many values in
$(n_{5/2}(\sigma ),-\dim (\sigma ))$
. This takes on finitely many values in
![]() $\mathbb {R}\times \mathbb {R}$
, so viewed lexicographically, the values are a finite totally ordered set, and adjacent (i.e., properly incident) simplices have different values, and hence this really can be viewed as a Morse function. The sublevel complex of all
$\mathbb {R}\times \mathbb {R}$
, so viewed lexicographically, the values are a finite totally ordered set, and adjacent (i.e., properly incident) simplices have different values, and hence this really can be viewed as a Morse function. The sublevel complex of all
![]() $\sigma $
with
$\sigma $
with
![]() $(n_{5/2}(\sigma ),-\dim (\sigma ))\le (0,0)$
equals
$(n_{5/2}(\sigma ),-\dim (\sigma ))\le (0,0)$
equals
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
. In particular, if we can show that the descending link of any
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
. In particular, if we can show that the descending link of any
![]() $\sigma $
with
$\sigma $
with
![]() $(n_{5/2}(\sigma ),-\dim (\sigma ))>(0,0)$
is contractible, then Morse theory will tell us that the inclusion of
$(n_{5/2}(\sigma ),-\dim (\sigma ))>(0,0)$
is contractible, then Morse theory will tell us that the inclusion of
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
into
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
into
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is a homotopy equivalence. (Intuitively, we attach the missing vertices in increasing order with respect to the Morse function, and at each stage we do so along a contractible descending link, so the homotopy type never changes.) To this end, suppose
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is a homotopy equivalence. (Intuitively, we attach the missing vertices in increasing order with respect to the Morse function, and at each stage we do so along a contractible descending link, so the homotopy type never changes.) To this end, suppose
![]() $(n_{5/2}(\sigma ),-\dim (\sigma ))>(0,0)$
, and we need to prove the descending link of
$(n_{5/2}(\sigma ),-\dim (\sigma ))>(0,0)$
, and we need to prove the descending link of
![]() $\sigma $
is contractible. The descending link is a join, of the descending face link spanned by all faces
$\sigma $
is contractible. The descending link is a join, of the descending face link spanned by all faces
![]() $\sigma ^\vee <\sigma $
with
$\sigma ^\vee <\sigma $
with
![]() $n_{5/2}(\sigma ^\vee )<n_{5/2}(\sigma )$
, and the descending coface link spanned by all proper cofaces
$n_{5/2}(\sigma ^\vee )<n_{5/2}(\sigma )$
, and the descending coface link spanned by all proper cofaces
![]() $\sigma ^\wedge>\sigma $
with
$\sigma ^\wedge>\sigma $
with
![]() $n_{5/2}(\sigma ^\wedge )=n_{5/2}(\sigma )$
. For any
$n_{5/2}(\sigma ^\wedge )=n_{5/2}(\sigma )$
. For any
![]() $5/2$
-disk D, there is a unique
$5/2$
-disk D, there is a unique
![]() $2$
-disk contained in it, which we will denote by
$2$
-disk contained in it, which we will denote by
![]() $\delta (D)$
. Let
$\delta (D)$
. Let
![]() $\sigma =\{D_0,\dots ,D_k\}$
. First, suppose that some
$\sigma =\{D_0,\dots ,D_k\}$
. First, suppose that some
![]() $D_i$
is a
$D_i$
is a
![]() $5/2$
-disk such that
$5/2$
-disk such that
![]() $\delta (D_i)\not \in \sigma $
. Then
$\delta (D_i)\not \in \sigma $
. Then
![]() $\sigma \cup \{\delta (D_i)\}$
is a descending proper coface of
$\sigma \cup \{\delta (D_i)\}$
is a descending proper coface of
![]() $\sigma $
, and moreover for any descending proper coface
$\sigma $
, and moreover for any descending proper coface
![]() $\sigma ^\wedge $
of
$\sigma ^\wedge $
of
![]() $\sigma $
, we have that
$\sigma $
, we have that
![]() $\sigma ^\wedge \cup \{\delta (D_i)\}$
is also a descending proper coface. The map
$\sigma ^\wedge \cup \{\delta (D_i)\}$
is also a descending proper coface. The map
![]() $\sigma ^\wedge \mapsto \sigma ^\wedge \cup \{\delta (D_i)\}$
, thus, induces a homotopy equivalence from the descending coface link to the (contractible) star of
$\sigma ^\wedge \mapsto \sigma ^\wedge \cup \{\delta (D_i)\}$
, thus, induces a homotopy equivalence from the descending coface link to the (contractible) star of
![]() $\sigma \cup \{\delta (D_i)\}$
, so the descending coface link is contractible (see, e.g., [Reference QuillenQui78, Section 1.5]). Now suppose that whenever
$\sigma \cup \{\delta (D_i)\}$
, so the descending coface link is contractible (see, e.g., [Reference QuillenQui78, Section 1.5]). Now suppose that whenever
![]() $D_i$
is a
$D_i$
is a
![]() $5/2$
-disk,
$5/2$
-disk,
![]() $\delta (D_i)\in \sigma $
. Let
$\delta (D_i)\in \sigma $
. Let
![]() $\sigma _0<\sigma $
be the (nonempty) face of
$\sigma _0<\sigma $
be the (nonempty) face of
![]() $\sigma $
consisting of all
$\sigma $
consisting of all
![]() $2$
-disks in
$2$
-disks in
![]() $\sigma $
. This is a descending face, and given any descending face
$\sigma $
. This is a descending face, and given any descending face
![]() $\sigma ^\vee <\sigma $
, we have that
$\sigma ^\vee <\sigma $
, we have that
![]() $\sigma ^\vee \cup \sigma _0$
is again a descending face of
$\sigma ^\vee \cup \sigma _0$
is again a descending face of
![]() $\sigma $
. Hence, the map
$\sigma $
. Hence, the map
![]() $\sigma ^\vee \mapsto \sigma ^\vee \cup \sigma _0$
induces a homotopy equivalence from the descending face link to the (contractible) star of
$\sigma ^\vee \mapsto \sigma ^\vee \cup \sigma _0$
induces a homotopy equivalence from the descending face link to the (contractible) star of
![]() $\sigma _0$
, so the descending face link is contractible.
$\sigma _0$
, so the descending face link is contractible.
We have shown that
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is homotopy equivalent to
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is homotopy equivalent to
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
, which is
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
, which is
![]() $\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -2\Big )$
-connected by Citation 4.9. Since higher connectivity of links is not necessarily preserved under homotopy equivalence, we have more work to do before we can conclude that
$\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -2\Big )$
-connected by Citation 4.9. Since higher connectivity of links is not necessarily preserved under homotopy equivalence, we have more work to do before we can conclude that
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
is wCM of dimension
![]() $\left \lfloor \frac {m+1}{3}\right \rfloor -1$
. Let
$\left \lfloor \frac {m+1}{3}\right \rfloor -1$
. Let
![]() $\sigma =\{D_0,\dots ,D_k\}$
be a k-simplex in
$\sigma =\{D_0,\dots ,D_k\}$
be a k-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
, and consider its link
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
, and consider its link
![]() in
in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
. Working with the barycentric subdivision as in the first paragraph, we can view L as the subcomplex spanned by all proper cofaces
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
. Working with the barycentric subdivision as in the first paragraph, we can view L as the subcomplex spanned by all proper cofaces
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
. If some
$\sigma $
. If some
![]() $D_i$
is a
$D_i$
is a
![]() $5/2$
-disk such that
$5/2$
-disk such that
![]() $\delta (D_i)\not \in \sigma $
, then the map
$\delta (D_i)\not \in \sigma $
, then the map
![]() $\tau \mapsto \tau \cup \{\delta (D_i)\}$
induces a homotopy equivalence from L to the star of the proper coface
$\tau \mapsto \tau \cup \{\delta (D_i)\}$
induces a homotopy equivalence from L to the star of the proper coface
![]() $\sigma \cup \{\delta (D_i)\}$
in L, and hence L is contractible. Now assume that whenever
$\sigma \cup \{\delta (D_i)\}$
in L, and hence L is contractible. Now assume that whenever
![]() $D_i$
is a
$D_i$
is a
![]() $5/2$
-disk,
$5/2$
-disk,
![]() $\delta (D_i)\in \sigma $
. Call
$\delta (D_i)\in \sigma $
. Call
![]() $D_i$
and
$D_i$
and
![]() $\delta (D_i)$
paired in this case. If
$\delta (D_i)$
paired in this case. If
![]() $D_i$
is a vertex of
$D_i$
is a vertex of
![]() $\sigma $
that is not paired, call it solitary (and note that the solitary vertices must be
$\sigma $
that is not paired, call it solitary (and note that the solitary vertices must be
![]() $2$
-disks). Say
$2$
-disks). Say
![]() $2p$
is the number of paired vertices in
$2p$
is the number of paired vertices in
![]() $\sigma $
, so
$\sigma $
, so
![]() $k-2p+1$
is the number of solitary vertices. Consider the surface
$k-2p+1$
is the number of solitary vertices. Consider the surface
![]() $\mathcal {S}_{b+p,m-3p}^g$
obtained by cutting along the boundary and removing the interior (and unmarking the marked point on the boundary) of each
$\mathcal {S}_{b+p,m-3p}^g$
obtained by cutting along the boundary and removing the interior (and unmarking the marked point on the boundary) of each
![]() $5/2$
-disk in
$5/2$
-disk in
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $\overline {\sigma }$
be the (possibly empty)
$\overline {\sigma }$
be the (possibly empty)
![]() $(k-2p)$
-simplex in
$(k-2p)$
-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
whose vertices are the solitary vertices of
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
whose vertices are the solitary vertices of
![]() $\sigma $
, now viewed as disks in
$\sigma $
, now viewed as disks in
![]() $\mathcal {S}_{b+p,m-3p}^g$
. It is clear that L is isomorphic to the link of
$\mathcal {S}_{b+p,m-3p}^g$
. It is clear that L is isomorphic to the link of
![]() $\overline {\sigma }$
in
$\overline {\sigma }$
in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
(which if
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
(which if
![]() $\overline {\sigma }$
is empty means the whole complex). If the desired result holds for
$\overline {\sigma }$
is empty means the whole complex). If the desired result holds for
![]() $\overline {\sigma }$
and
$\overline {\sigma }$
and
![]() $\mathcal {S}_{b+p,m-3p}^g$
, then the link of
$\mathcal {S}_{b+p,m-3p}^g$
, then the link of
![]() $\overline {\sigma }$
in
$\overline {\sigma }$
in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
(and hence also L) is
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b+p,m-3p}^g)$
(and hence also L) is
![]() $\left (\left \lfloor \frac {(m-3p)+1}{3}\right \rfloor -(k-2p)-3\right )$
-connected, and hence
$\left (\left \lfloor \frac {(m-3p)+1}{3}\right \rfloor -(k-2p)-3\right )$
-connected, and hence
![]() $\big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected, i.e., the desired result holds for
$\big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected, i.e., the desired result holds for
![]() $\sigma $
and
$\sigma $
and
![]() $\mathcal {S}_{b,m}^g$
. Thus, it remains only to prove the result in the case when all the vertices of
$\mathcal {S}_{b,m}^g$
. Thus, it remains only to prove the result in the case when all the vertices of
![]() $\sigma $
are solitary.
$\sigma $
are solitary.
Since we have reduced to a case where all the vertices of
![]() $\sigma $
are
$\sigma $
are
![]() $2$
-disks, we can consider the subcomplex
$2$
-disks, we can consider the subcomplex
![]() $L_2$
of L that is the link of
$L_2$
of L that is the link of
![]() $\sigma $
in the subcomplex
$\sigma $
in the subcomplex
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
of
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
of
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
. Since
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
. Since
![]() ${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
is wCM of dimension
${\mathbb {D}}_2(\mathcal {S}_{b,m}^g)$
is wCM of dimension
![]() $\left \lfloor \frac {m+1}{3}\right \rfloor -1$
by Corollary 4.10, we know that
$\left \lfloor \frac {m+1}{3}\right \rfloor -1$
by Corollary 4.10, we know that
![]() $L_2$
is
$L_2$
is
![]() $\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected. Now we will build up from
$\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected. Now we will build up from
![]() $L_2$
to L by gluing in the missing simplices
$L_2$
to L by gluing in the missing simplices
![]() $\tau $
. We can again use the Morse function
$\tau $
. We can again use the Morse function
![]() $(n_{5/2},-\dim )$
, now restricted to L, since
$(n_{5/2},-\dim )$
, now restricted to L, since
![]() $L_2$
is precisely the sublevel complex of L defined by
$L_2$
is precisely the sublevel complex of L defined by
![]() $(n_{5/2},-\dim )\le (0,0)$
. If we can show that the descending link of any simplex in
$(n_{5/2},-\dim )\le (0,0)$
. If we can show that the descending link of any simplex in
![]() $L\setminus L_2$
is
$L\setminus L_2$
is
![]() $\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-4\big )$
-connected, then discrete Morse theory (see, e.g., [Reference Bashwinger and ZaremskyBB97, Corollary 2.6]) will tell us that L is
$\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-4\big )$
-connected, then discrete Morse theory (see, e.g., [Reference Bashwinger and ZaremskyBB97, Corollary 2.6]) will tell us that L is
![]() $\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected and we will be done. The argument from the first paragraph works in exactly the same way to show that the descending link in L of a simplex
$\Big (\left \lfloor \frac {m+1}{3}\right \rfloor -k-3\Big )$
-connected and we will be done. The argument from the first paragraph works in exactly the same way to show that the descending link in L of a simplex
![]() $\tau $
in
$\tau $
in
![]() $L\setminus L_2$
is contractible, except in one case, namely when every disk in
$L\setminus L_2$
is contractible, except in one case, namely when every disk in
![]() $\tau \setminus \sigma $
is a
$\tau \setminus \sigma $
is a
![]() $5/2$
-disk that is paired with a
$5/2$
-disk that is paired with a
![]() $2$
-disk in
$2$
-disk in
![]() $\sigma $
(see Figure 8 for a visualization of this situation). In this case, the descending face link of
$\sigma $
(see Figure 8 for a visualization of this situation). In this case, the descending face link of
![]() $\tau $
in L is the entire boundary of
$\tau $
in L is the entire boundary of
![]() $\tau $
(since removing any proper subset of disks in
$\tau $
(since removing any proper subset of disks in
![]() $\tau \setminus \sigma $
is a descending move), so if
$\tau \setminus \sigma $
is a descending move), so if
![]() $\tau $
is an
$\tau $
is an
![]() $\ell $
-simplex in L (i.e., a
$\ell $
-simplex in L (i.e., a
![]() $(k+\ell +1)$
-simplex in
$(k+\ell +1)$
-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
containing the k-simplex
${\mathbb {D}}_{2,5/2}(\mathcal {S}_{b,m}^g)$
containing the k-simplex
![]() $\sigma $
), then the descending face link of
$\sigma $
), then the descending face link of
![]() $\tau $
in L is an
$\tau $
in L is an
![]() $(\ell -1)$
-sphere, hence
$(\ell -1)$
-sphere, hence
![]() $(\ell -2)$
-connected. In this case, we can also understand the descending coface link of
$(\ell -2)$
-connected. In this case, we can also understand the descending coface link of
![]() $\tau $
in L: it is isomorphic to the
$\tau $
in L: it is isomorphic to the
![]() $2$
-disk complex on the surface obtained by cutting out all the disks in
$2$
-disk complex on the surface obtained by cutting out all the disks in
![]() $\tau $
. Since each disk in
$\tau $
. Since each disk in
![]() $\tau \setminus \sigma $
contains a disk in
$\tau \setminus \sigma $
contains a disk in
![]() $\sigma $
, this produces
$\sigma $
, this produces
![]() $k+1$
new boundary components and eliminates
$k+1$
new boundary components and eliminates
![]() $2(k+1)+(\ell +1)=2k+\ell +3$
marked points, so this surface is
$2(k+1)+(\ell +1)=2k+\ell +3$
marked points, so this surface is
![]() $\mathcal {S}_{b+k+1,m-2k-\ell -3}^g$
. The
$\mathcal {S}_{b+k+1,m-2k-\ell -3}^g$
. The
![]() $2$
-disk complex of this surface, and hence the descending coface link of
$2$
-disk complex of this surface, and hence the descending coface link of
![]() $\tau $
, is
$\tau $
, is
![]() $\left (\left \lfloor \frac {(m-2k-\ell -3)+1}{3}\right \rfloor -2\right )$
-connected. Joining this with the descending face link, which is
$\left (\left \lfloor \frac {(m-2k-\ell -3)+1}{3}\right \rfloor -2\right )$
-connected. Joining this with the descending face link, which is
![]() $(\ell -2)$
-connected, we get that the descending link of
$(\ell -2)$
-connected, we get that the descending link of
![]() $\tau $
is
$\tau $
is
![]() $\left (\left \lfloor \frac {(m-2k-\ell -3)+1}{3}\right \rfloor +\ell -2\right )$
-connected. We need it to be
$\left (\left \lfloor \frac {(m-2k-\ell -3)+1}{3}\right \rfloor +\ell -2\right )$
-connected. We need it to be
![]() $\left (\left \lfloor \frac {m+1}{3}\right \rfloor -k-4\right )$
-connected, so it suffices to prove that
$\left (\left \lfloor \frac {m+1}{3}\right \rfloor -k-4\right )$
-connected, so it suffices to prove that
![]() $\left \lfloor \frac {m+1}{3}\right \rfloor -k-1 \le \left \lfloor \frac {m+1}{3} - \frac {2k+\ell }{3}\right \rfloor +\ell $
. This is indeed true by the following calculation:
$\left \lfloor \frac {m+1}{3}\right \rfloor -k-1 \le \left \lfloor \frac {m+1}{3} - \frac {2k+\ell }{3}\right \rfloor +\ell $
. This is indeed true by the following calculation:
 $$ \begin{align*} \left\lfloor\frac{m+1}{3}\right\rfloor-k-1 &= \left\lfloor\frac{m+1}{3} - \frac{3k+3}{3}\right\rfloor \\ &\le \left\lfloor\frac{m+1}{3} - \frac{2k-2\ell}{3}\right\rfloor \\ &\le \left\lfloor\frac{m+1}{3} - \frac{2k+\ell}{3}\right\rfloor+\ell.\\[-38pt] \end{align*} $$
$$ \begin{align*} \left\lfloor\frac{m+1}{3}\right\rfloor-k-1 &= \left\lfloor\frac{m+1}{3} - \frac{3k+3}{3}\right\rfloor \\ &\le \left\lfloor\frac{m+1}{3} - \frac{2k-2\ell}{3}\right\rfloor \\ &\le \left\lfloor\frac{m+1}{3} - \frac{2k+\ell}{3}\right\rfloor+\ell.\\[-38pt] \end{align*} $$

Figure 8: An example of the last case in the proof of Proposition 5.12 (for the surface
![]() $\mathcal {S}_8$
). The disks bounded in red comprise
$\mathcal {S}_8$
). The disks bounded in red comprise
![]() $\sigma $
, and the disks bounded in blue comprise
$\sigma $
, and the disks bounded in blue comprise
![]() $\tau \setminus \sigma $
. Hence,
$\tau \setminus \sigma $
. Hence,
![]() $\sigma $
is a
$\sigma $
is a
![]() $2$
-simplex and
$2$
-simplex and
![]() $\tau $
is a
$\tau $
is a
![]() $4$
-simplex in
$4$
-simplex in
![]() ${\mathbb {D}}_{2,5/2}(\mathcal {S}_8)$
containing
${\mathbb {D}}_{2,5/2}(\mathcal {S}_8)$
containing
![]() $\sigma $
, so
$\sigma $
, so
![]() $\tau $
represents a
$\tau $
represents a
![]() $1$
-simplex in
$1$
-simplex in
![]() $L=\operatorname {lk}\sigma $
.
$L=\operatorname {lk}\sigma $
.
Now we can prove the main result of this section, that
![]() $\operatorname {br}\!R$
is of type
$\operatorname {br}\!R$
is of type
![]() $\operatorname {\mathrm {F}}_\infty $
.
$\operatorname {\mathrm {F}}_\infty $
.
Acknowledgment
We are grateful to Daniel Allcock, Jim Belk, and Xiaolei Wu for helpful discussions, to Anthony Genevois for pointing out the reference [Reference Bestvina and BradyBGdlH13], and to the anonymous referee for some excellent suggestions.