Published online by Cambridge University Press: 20 November 2018
A lattice L is called transferable if and only if, whenever L can be embedded in the ideal lattice I(K) of a lattice K, L can be embedded in K. L is called sharply transferable if and only if, for every lattice embedding ψ(x) , there exists an embedding 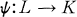 such that for x, y ϵ L,
such that for x, y ϵ L, 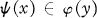 if and only if x ≤ y. Finite sharply transferable lattices were characterized in [3]. In this paper we extend the characterization to the infinite case. We begin by revising some of the terminology of [3].
if and only if x ≤ y. Finite sharply transferable lattices were characterized in [3]. In this paper we extend the characterization to the infinite case. We begin by revising some of the terminology of [3].
1.1. Definition, (a) Let 〈P; ≧〉 be a poset and X, Y ⊆ P. Then X dominates Y (written X Dom Y) if and only if, for every y ∈ F, there exists x ∈ X such that y ∈ x. Dually, X supports Y (written X Spp Y) if and only if, for every y ∈ Y, there exists x ∈ X such that x ≦ y.