Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T07:36:20.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying Algebras for the K-Theory of σ-C*-Algebras

Published online by Cambridge University Press:  20 November 2018

N. Christopher Phillips
N. Christopher Phillips*
Affiliation:
University of Georgia, Athens, Georgia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In topology, the representable K-theory of a topological space X is defined by the formulas RK0(X) = [X,Z x BU] and RKl(X) = [X, U], where square brackets denote sets of homotopy classes of continuous maps, 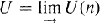is the infinite unitary group, and BU is a classifying space for U. (Note that ZxBU is homotopy equivalent to the space of Fredholm operators on a separable infinite-dimensional Hilbert space.) These sets of homotopy classes are made into abelian groups by using the H-group structures on Z x BU and U. In this paper, we give analogous formulas for the representable K-theory for α-C*-algebras defined in [20].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 6 , 01 December 1989 , pp. 1021 - 1089
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Adams, J. F., Stable homotopy and generalized homology, part III, Chicago Lectures in Mathematics (University of Chicago Press, 1974).Google Scholar
2. Anderson, J., Blackadar, B.and Haagerup, U., Minimal projections in the reduced group C*- algebra ofZn * Zm, J. Operator Theory, to appear.Google Scholar
3. Blackadar, B., A simple C*-algebra with no nontrivial projections, Proc. Amer. Math. Soc. 78 (1980), 504–508.Google Scholar
4. Blackadar, B., shape theory for C*-algebras, Math. Scand. 56 (1985), 249–275.Google Scholar
5. Blackadar, B., K-theory for operator algebras, MSRI publications no. 5 (Springer-Verlag, New York, Berlin, Heidelberg, London, Paris, Tokyo, 1986).Google Scholar
6. Blackadar, B., Comparison theory in simple C*-algebras, pages 21–54 in: Operator algebras and applications Volume 1 : Structure theory; K-theory, geometry and topology, London Mathematical Society Lecture Note Series no. 135 (Cambridge University Press, Cambridge, New York, New Rochelle, Melbourne, Sydney, 1988).Google Scholar
7. Brown, L. G., Ext of certain free product C*- algebras, J. Operator Theory 6 (1981), 135–141.Google Scholar
8. Cuntz, J., A new look at KK-theory, -Theory / (1987), 31–51.Google Scholar
9. Cuntz, J.and Higson, N., Kuiper's theorem for Hilbert modules, pages 429–435 in: Operator algebras and mathematical physics, Contemporary Math. 62 (Amer. Math. Soc, 1987).Google Scholar
10. Effros, E. G. and Kaminker, J., Homotopy continuity and shape theory for C*-algebras, pages 152–180 in: Geometric methods in operator algebras, Pitman Research Notes in Math. 123 (Longman Scientific and Technical, 1986).Google Scholar
11. Karoubi, M., K-theory: an introduction, Grundlehren der Mathematischen Wissenschaften 226 (Springer-Verlag, Berlin, Heidelberg, New York, 1978).Google Scholar
12. Kasparov, G. G., The operator K-functor and extensions of C*-algebras, Izv. Akad. Nauk SSSR, Ser. Mat. 44 (1980), 571–636 (in Russian); English translation in Math. USSR Izvestija 16 (1981), 513–572.Google Scholar
13. Loring, T. A., The torus and noncommutative topology, Ph.D. Thesis, Berkeley (1986).Google Scholar
14. MacLane, S., Categories for the working mathematician, Graduate Texts in Math 5 (Springer- Verlag, Berlin, Heidelberg, New York, 1971).Google Scholar
15. Mingo, J. A., K-theory and multipliers of stable C*-algebras, Trans. Amer. Math. Soc. 299 (1987), 397–411.Google Scholar
16. Mingo, J. A. and Phillips, W. J., Equivariant triviality theorems for Hubert C*-modules, Proc. Amer. Math. Soc. 91 (1984), 225–230.Google Scholar
17. Pedersen, G. K., SAW*-algebras and corona C*-algebras, contributions to noncommutative topology, J. Operator Theory 75 (1986), 15–32.Google Scholar
18. Phillips, N. C., Equivariant K-theory and freeness of group actions on C*-algebras, Lecture Notes in Math. 1274 (Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo, 1987).Google Scholar
19. Phillips, N. C., Inverse limits of C*-algebras, J. Operator Theory 19 (1988), 159–195.Google Scholar
20. Phillips, N. C., Representable K-theory for cr-C*-algebras, K-Theory, to appear.Google Scholar
21. Phillips, N. C., Inverse limits of C*-algebras and applications, pages 127–185 in: Operator algebras and applications Volume 1: Structure theory; K-theory, geometry and topology, London Mathematical Society Lecture Note Series 135 (Cambridge University Press, Cambridge, New York, New Rochelle, Melbourne, Sydney, 1988).Google Scholar
22. Rosenberg, J., The role of K-theory in noncommutative algebraic topology, pages 155–182 in: Operator algebras and K-theory, Contemporary Math. 10 (Amer. Math. Soc, 1982).Google Scholar
23. Schochet, C., Topological methods for C*-algebras II: geometric resolutions and the Kunneth formula, Pacific J. Math. 98 (1982), 443–458.Google Scholar
24. Schochet, C., Topological methods for C*-algebras IV: mod p homology, Pacific J. Math. 114 (1984), 447–168.Google Scholar
25. Spanier, E., Quasitopologies, Duke Math. J. 30 (1963), 1–14.Google Scholar
26. Spanier, E., Algebraic topology (McGraw-Hill, New York, San Francisco, St. Louis, Toronto, London, Sydney, 1966).Google Scholar
27. Switzer, R. M., Algebraic topology - homotopy and homology, Grundlehren der Mathematischen Wissenschaften 212 (Springer-Verlag, Berlin, Heidelberg, New York, 1975).Google Scholar
28. Takesaki, M., Theory of operator algebras I (Springer-Verlag, New York, Heidelberg, Berlin, 1979).Google Scholar
29. Voiculescu, D., Dual algebraic structures on operator algebras related to free products, J. Operator Theory 17 (1987), 85–98.Google Scholar
30. Weidner, J., Topological invariants for generalized operator algebras, Ph.D. Thesis, Heidelberg (1987).Google Scholar
31. Whitehead, G. W., Elements of homotopy theory, Graduate Texts in Math. 61 (Springer-Verlag, New York, Heidelberg, Berlin, 1978).Google Scholar
32. Zekri, R., A new description of Kasparov's theory of C*-algebra extensions, Ph.D. Thesis, Université d'Aix-Marseille II, Faculté des Sciences de Luminy (1986).Google Scholar