Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T15:22:43.877Z Has data issue: false hasContentIssue false
  • English
  • Français

A Complete Classification of AI Algebras with the Ideal Property

Published online by Cambridge University Press:  20 November 2018

Kui Ji  and
Chunlan Jiang
Kui Ji
Affiliation:
Department of Mathematics, Hebei Normal University, Shijiazhuang 050016, China email: jikuikui@gmail.comcljiang@hebtu.edu.cn
Chunlan Jiang
Affiliation:
Department of Mathematics, Hebei Normal University, Shijiazhuang 050016, China email: jikuikui@gmail.comcljiang@hebtu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $A$ be an 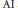$\text{AI}$ algebra; that is, $A$ is the 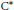${{\text{C}}^{*}}$-algebra inductive limit of a sequence

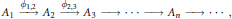$${{A}_{1}}\xrightarrow{{{\phi }_{1,2}}}{{A}_{2}}\xrightarrow{{{\phi }_{2,3}}}{{A}_{3}}\to \cdot \cdot \cdot \to {{A}_{n}}\to \cdot \cdot \cdot ,$$

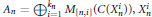where ${{A}_{n}}=\oplus _{i=1}^{{{k}_{n}}}{{M}_{\left[ n,i \right]}}\left( C\left( X_{n}^{i} \right) \right),X_{n}^{i}$ are [0, 1], 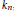${{k}_{n}}$, and 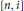$\left[ n,\,i \right]$ are positive integers. Suppose that $A$ has the ideal property: each closed two-sided ideal of $A$ is generated by the projections inside the ideal, as a closed two-sided ideal. In this article, we give a complete classification of 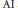$\text{AI}$ algebras with the ideal property.

Keywords

46L3519K1446L0546L08AI algebrasK-grouptracial stateideal propertyclassification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 2 , 01 April 2011 , pp. 381 - 412
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Dadarlat, M. and Gong, G., A classification result for approximately homogeneous C¤-algebras of real rank zero. Geom. Funct. Anal. 7(1997), no. 4, 646–711. doi:10.1007/s000390050023Google Scholar
[2] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew. Math. 443(1993), 179–219.Google Scholar
[3] Elliott, G. A., A classification of certain simple C¤-algebras. In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer Acad. Publ., Dordrecht, 1993, pp. 373–385.Google Scholar
[4] Elliott, G. A., A classification of certain simple C¤-algebra. II. J. Ramanujan Math. Soc. 12(1997), no. 1, 97–134.Google Scholar
[5] Elliott, G. A. and Gong, G., On the classification of C¤-algebras of real rank zero. II. Ann. of Math. 144(1996), no. 3, 497–610. doi:10.2307/2118565Google Scholar
[6] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C¤-algebra II. The isomorphism theorem. Invent. Math. 168(2007), no. 2, 249–320. doi:10.1007/s00222-006-0033-yGoogle Scholar
[7] Gong, G., On the classification of simple inductive limit C¤-algebras. I. The reduction theorem. Doc. Math. 7(2002), 255–461.Google Scholar
[8] Gong, G., Jiang, C., Li, L., and Paniscu, C., AT structure of AH algebras with the ideal property and torsion free K-theory. J. Funct. Anal. 258(2010), no. 6, 2119–2143. doi:10.1016/j.jfa.2009.11.016Google Scholar
[9] Li, L., Simple inductive limit C¤-algebras: spectra and approximations by interval algebras. J. Reine Angew. Math. 507(1999), 57–79.Google Scholar
[10] Li, L., On the classification of simple C¤-algebras: inductive limits of matrix algebras over trees. Mem. Amer. Math. Soc. 127(1997), no. 605.Google Scholar
[11] Li, L., Classification of simple C¤-algebra: inductive limits of matrix algebras over one-dimensional spaces. J. Funct. Anal. 192(2002), no. 1, 1–51. doi:10.1006/jfan.2002.3895Google Scholar
[12] Pasnicu, C., Shape equivalence, nonstable K-theory and AH algebras. Pacific J. Math. 192(2000), no. 1, 159–182. doi:10.2140/pjm.2000.192.159Google Scholar
[13] Stevens, K. H., The classification of certain non-simple approximate interval algebras. In: Operator algebras and their applications, II (Waterloo, ON, 1994/1995), Fields Inst. Commun., 20, American Mathematical Society, Providence, RI, 1998, pp. 105–148.Google Scholar
[14] Su, H., On the classification of C¤-algebras of real rank zero: inductive limits of matrix algebras over non-Hausdorff graphs. Mem. Amer. Math. Soc.114(1995), no. 547.Google Scholar
[15] Thomsen, K., Limits of certain subhomogeneous C¤-algebras. Mém. Soc. Math. Fr. 71(1999).Google Scholar
[16] Wegge-Olsen, N. E., K-theory and C¤-algebras. A friendly approach. Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1993.Google Scholar