No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let S be a subset of some linear topological space. The set S is said to be m-convex, m ≧ 2, if and only if for every m-member subset of S, at least one of the 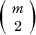 line segments determined by these points lies in S. A point x in S is said to be a point of local convexity of S if and only if there is some neighborhood N of x such that if y, z Є N ⌒ S, then [y, z] ⊆ S. If S fails to be locally convex at some point a in S, then q is called a point of local nonconvexity (lnc point) of S.
line segments determined by these points lies in S. A point x in S is said to be a point of local convexity of S if and only if there is some neighborhood N of x such that if y, z Є N ⌒ S, then [y, z] ⊆ S. If S fails to be locally convex at some point a in S, then q is called a point of local nonconvexity (lnc point) of S.