Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Serre, Jean-Pierre
2000.
Oeuvres - Collected Papers IV.
p.
637.
Garibaldi, R.Skip
2001.
Structurable Algebras and Groups of Type E6 and E7.
Journal of Algebra,
Vol. 236,
Issue. 2,
p.
651.
Reichstein, Zinovy
and
Youssin, Boris
2001.
Splitting fields of G-varieties.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
207.
Reichstein, Z.
and
Youssin, B.
2001.
On a property of special groups.
Transformation Groups,
Vol. 6,
Issue. 3,
p.
261.
Reichstein, Z.
and
Youssin, B.
2002.
Conditions satisfied by characteristic polynomials in fields and division algebras.
Journal of Pure and Applied Algebra,
Vol. 166,
Issue. 1-2,
p.
165.
Reichstein, Z.
and
Youssin, B.
2002.
A birational invariant for algebraic group actions.
Pacific Journal of Mathematics,
Vol. 204,
Issue. 1,
p.
223.
Rowen, Louis H.
2003.
Proceedings of the Third International Algebra Conference.
p.
221.
Reichstein, Z.
and
Youssin, B.
2003.
A non-split torsor with trivial fixed point obstruction.
Journal of Algebra,
Vol. 263,
Issue. 2,
p.
255.
Berhuy, G.
and
Reichstein, Z.
2005.
On the notion of canonical dimension for algebraic groups.
Advances in Mathematics,
Vol. 198,
Issue. 1,
p.
128.
Cramer, Ronald
Daza, Vanesa
Gracia, Ignacio
Urroz, Jorge Jiménez
Leander, Gregor
Martí-Farré, Jaume
and
Padró, Carles
2005.
Advances in Cryptology – CRYPTO 2005.
Vol. 3621,
Issue. ,
p.
327.
Chernousov, Vladimir
and
Serre, Jean-Pierre
2006.
Lower bounds for essential dimensions via orthogonal representations.
Journal of Algebra,
Vol. 305,
Issue. 2,
p.
1055.
TOKUNAGA, Hiro-o
2006.
TWO-DIMENSIONAL VERSAL G-COVERS AND CREMONA EMBEDDINGS OF FINITE GROUPS.
Kyushu Journal of Mathematics,
Vol. 60,
Issue. 2,
p.
439.
Chernousov, V.
Gille, P.
and
Reichstein, Z.
2006.
Resolving G -torsors by abelian base extensions.
Journal of Algebra,
Vol. 296,
Issue. 2,
p.
561.
MacDONALD, MARK L.
2008.
Cohomological invariants of odd degree Jordan algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 145,
Issue. 2,
p.
295.
Karpenko, Nikita A.
and
Merkurjev, Alexander S.
2008.
Essential dimension of finite p-groups.
Inventiones mathematicae,
Vol. 172,
Issue. 3,
p.
491.
Favi, Giordano
and
Florence, Mathieu
2008.
Tori and essential dimension.
Journal of Algebra,
Vol. 319,
Issue. 9,
p.
3885.
Cramer, Ronald
Daza, Vanesa
Gracia, Ignacio
Urroz, Jorge JimÉnez
Leander, Gregor
Marti-Farre, Jaume
and
Padro, Carles
2008.
On Codes, Matroids, and Secure Multiparty Computation From Linear Secret-Sharing Schemes.
IEEE Transactions on Information Theory,
Vol. 54,
Issue. 6,
p.
2644.
Budur, Nero
2009.
Unitary local systems, multiplier ideals, and polynomial periodicity of Hodge numbers.
Advances in Mathematics,
Vol. 221,
Issue. 1,
p.
217.
Meyer, Aurel
and
Reichstein, Zinovy
2009.
The essential dimension of the normalizer of a maximal torus in the projective linear group.
Algebra & Number Theory,
Vol. 3,
Issue. 4,
p.
467.
Baek, Sanghoon
and
Merkurjev, Alexander S.
2009.
Invariants of simple algebras.
manuscripta mathematica,
Vol. 129,
Issue. 4,
p.
409.






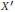 ${{X}^{'}}$ with the following property: the stabilizer of every point of
${{X}^{'}}$ with the following property: the stabilizer of every point of 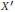 ${{X}^{'}}$ is isomorphic to a semidirect product
${{X}^{'}}$ is isomorphic to a semidirect product 

