Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T17:15:38.601Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Pq-Algebras

Published online by Cambridge University Press:  20 November 2018

Pierre Antoine Grillet
Pierre Antoine Grillet*
Affiliation:
Kansas State University, Manhattan Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a PQ (product-quotients) algebra, we mean a non-empty set 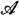together with three single-valued and not necessarily associative operations ., / , \ that we shall treat as product, right quotient, and left quotient although we require no relation between them. The theory of binary systems provides the following examples:

A. 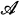is the set of all subsets of a groupoid G (which may be a semigroup) with the operations defined by:

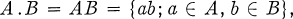
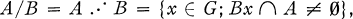
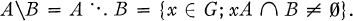
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 582 - 595
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Bruck, R. H., A survey of binary systems (Springer-Verlag, Berlin-Gôttingen-Heidelberg, 1958).10.1007/978-3-662-35338-7CrossRefGoogle Scholar
2. Croisot, R., Equivalences principales bilatères définies dans un demi-groupe, J. Math. Pures Appl. (9), 86 (1957), 373–417.Google Scholar
3. Desq, R., Etude dans un demi-groupe D d'une relation à*équivalence liée à un complexe H, C. R. Acad. Sci. Paris, 254 (1962), 2117–2119.Google Scholar
4. Dubreil, P., Contribution à la théorie des demi-groupes, Mém. Acad. Sci. Paris, 68 (1941), 52 pp.Google Scholar
5. Dubreil-Jacotin, M.-L., Lesieur, L., and Croisot, R., Leçons sur la théorie des treillis, des structures algébriques ordonnées et des treillis géométriques, Gauthier-Villars, Paris, 1953.Google Scholar
6. Grillet, P.-A., Equivalences compatibles, équivalences prépermises, Séminaire Dubreil-Pisot Univ. de Paris), 15 (1961/62), numéro 2.Google Scholar
7. Grillet, P.-A., Les applications de préfermeture, C. R. Acad. Sci. Paris, 258 (1961), 2824–2826.Google Scholar
8. Grillet, P.-A., Homomorphismes principaux de tas et de groupoïdes (Thèse Sci. Math.), Bull. Soc. Math. France, Mém. numéro 3 (1965).Google Scholar
9. Lefebvre, P., Sur la plus fine équivalence régulière et simplifiable d'un demi-groupe, C. R. Acad. Sci. Paris, 251 (1960), 1265–1267.Google Scholar
10. Mattenet, G., Sur les quasi-group es, Séminaire Dubreil-Pisot (Univ. de Paris), 15 (1961/62), numéro 12.Google Scholar