Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T01:54:40.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Frobenius Induction for Higher Whitehead Groups

Published online by Cambridge University Press:  20 November 2018

Andrew J. Nicas
Andrew J. Nicas*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of induced representations has served as a powerful tool in the computations of algebraic K-theory and L-theory ([2], [7], [4, 5], [9], [10, 11, 12, 13], [14], [17], [18]). In this paper we show how to apply this theory to obtain induction theorems for the higher Whitehead groups of Waldhausen. The same technique applies to the analogs of Whitehead groups in unitary K-theory and in L-theory.

For any ring A with unit, let K(A) be the spectrum of the algebraic K-theory of A ([8, p. 343]). Given a discrete group Γ and a subring R of the rational numbers, Loday defines a map of spectra:

*

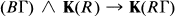
where (BΓ) is the classifying space of Γ union with a disjoint base point and RΓ is the group-ring of Γ over R.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 1 , 01 February 1987 , pp. 222 - 238
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Adams, J. F., Infinite loop spaces, Annals of Math. Studies 90 (Princeton Univ. Press, 1978).CrossRefGoogle Scholar
2. Dress, A. W. M., Induction and structure theorems for orthogonal representations of finite groups, Ann. of Math. 102 (1975), 291–325.Google Scholar
3. Evens, L., A generalization of the transfer map in the cohomology of groups, Trans. Amer. Math. Soc. 108 (1963), 54–65.Google Scholar
4. Farrell, F. T. and Hsiang, W.-C., The topological Euclidean space form problem, Invent. Math. 45 (1978), 181–192.Google Scholar
5. Farrell, F. T. and Hsiang, W.-C., On the rational homotopy groups of the diffeomorphism groups of discs, spheres, and aspherical manifolds, Proc. Symp. Pure Math. 32 (1978), 3–22.Google Scholar
6. Kahn, D. and Priddy, S., Applications of the transfer to stable homotopy theory, Bull. Amer. Math. Soc. 78 (1972), 981–987.Google Scholar
7. Lam, T.-Y., Induction theorems for Grothendieck groups and Whitehead groups of finite groups, Ann. Scient. Ec. Norm. Sup. 1 (1968), 91–148.Google Scholar
8. Loday, J., K-théorie algébrique et représentations de groupes, Ann. Scient. Ec. Norm. Sup. 9 (1976), 306–377.Google Scholar
9. Madsen, I., Smooth spherical space forms, geometric applications of homotopy theory I, Proceedings, Evanston 1977 (Lecture Notes in Math. 657, Springer-Verlag, 1978) 301–352.Google Scholar
10. Nicas, A., Induction theorems for groups of homotopy manifold structures, Memoirs of the Amer. Math. Soc. 267 (1982).Google Scholar
11. Nicas, A., On Wh2 of a Bieberbach group, Topology 22 (1984), 313–321.Google Scholar
12. Nicas, A., On Wh3 of a Bieberbach group, Math. Proc. Camb. Phil. Soc. 95 (1984), 55–60.Google Scholar
13. Nicas, A., On the higher Whitehead groups of a Bieberbach group, Trans. Amer. Math. Soc. 22 (1985), 853–859.Google Scholar
14. Nicas, A. and Stark, C., Whitehead groups of certain hyperbolic manifolds, Math. Proc. Camb. Phil. Soc. 95 (1984), 299–308.Google Scholar
15. Quillen, D., Higher algebraic K-theory I, Algebraic K-theory I, Lecture Notes in Math. 341 (Springer-Verlag, 1973), 85–147.Google Scholar
16. Ranicki, A., Exact sequences in the algebraic theory of surgery, (Princeton Univ. Press, 1981).Google Scholar
17. Stark, C. W., Structure sets vanish for certain bundles over Siefert manifolds, Trans. Amer. Math. Soc. 285 (1984), 603–615.Google Scholar
18. Swan, R. G., K-theory of finite groups and orders, Lecture Notes in Math. 149 (Springer-Verlag, 1970).CrossRefGoogle Scholar