Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T05:17:02.624Z Has data issue: false hasContentIssue false
  • English
  • Français

High Level Occupation Times for Gaussian Stochastic Processes with Sample Paths in Orlicz Spaces

Published online by Cambridge University Press:  20 November 2018

Anna T. Lawniczak
Anna T. Lawniczak*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a complete separable metric space, and 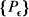a family of probability measures on the Borel subsets of X. We say that 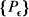obeys the large deviation principle (LDP) with a rate function I(·) if there exists a function I(·) from X into [0, ∞] satisfying:

  • (i) 0 ≦ I(x) ≦ ∞ for all x ∊ X.

  • (ii) I(·) is lower semicontinuous.

  • (iii) For each l < ∞ the set {x:I(x) ≦ l} is a compact set in X.

  • (iv) For each closed set C ⊂ X

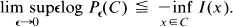
  • (v) For each open set C ⊂ X

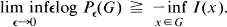
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 1 , 01 February 1987 , pp. 239 - 256
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Byczkowski, T., Gaussian measures on Lp spaces, 0 < p < ∞, Studia Math. 59 (1977), 249–261.Google Scholar
2. Byczkowski, T., Norm convergent expansion for Lϕ-valued Gaussian random elements, Studia Math. 64(1979), 87–95.Google Scholar
3. Donsker, M.D. and Varadhan, S.R.S., Asymptotic evaluation of certain Markov processes expectations for large time — III, Comm. Pure Appl. Math. 29 (1976), 389–461.Google Scholar
4. Halmos, P.R., Measure theory, (New York, Springer-Verlag, 1974).Google Scholar
5. Hille, E. and Phillips, R., Functional analysis and semigroups, AMS Colloquium Publications, 31 (1975).Google Scholar
6. Kallianpur, G. and Oodaira, H., Freidlin-Wentzell type estimates for abstract Wiener spaces, Sankhyà 40, Series A (1978), 116–137.Google Scholar
7. Lawniczak, A.T., Gaussian measures on Orlicz spaces and abstract Wiener spaces, Lecture Notes in Mathematics 939 (Springer-Verlag, 1982), 81–97.Google Scholar
8. Lawniczak, A.T., Gaussian measures on Orlicz spaces, Stoch. Analysis and its Appl. 3 (1985).Google Scholar
9. Marlow, N., High level occupation times for continuous Gaussian processes, Ann. of Probab. 3 (1973), 388–397.Google Scholar
10. Rolewicz, S., Metric linear spaces, (Polish Scientific Publishers, PWN, 1972).Google Scholar
11. Strook, D.W., An introduction to the theory of large deviations, (Springer-Verlag, 1984).CrossRefGoogle Scholar
12. Varadhan, S.R.S., Large deviations and applications, SIAM (1984).CrossRefGoogle Scholar