Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T01:24:25.252Z Has data issue: false hasContentIssue false
  • English
  • Français

Idempotents in Complex Banach Algebras

Published online by Cambridge University Press:  20 November 2018

G. N. Hile  and
W. E. Pfaffenberger
G. N. Hile
Affiliation:
University of Hawaii, Honolulu, Hawaii
W. E. Pfaffenberger
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The concept of the spectrum of A relative to Q, where A and Q commute and are elements in a complex Banach algebra 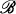with identity I, was developed in [1]. A complex number z is in the Q-resolvent set of A if and only if 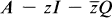is invertible in 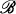otherwise, z is in the Q-spectrum of A, or spectrum of A relative to Q. One result from [1] was the following.

THEOREM. Suppose no points in the ordinary spectrum of Q have unit magnitude. Let C be a simple closed rectifiable curve which lies in the Q-resolvent of A, and let

*

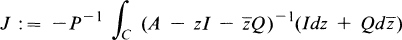
where P is defined asxs

•

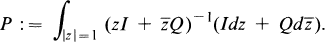
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 625 - 630
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Hile, G. N. and Pfaffenberger, W. E., Generalized spectral theory in complex Banach algebras, Can. J. Math. 37 (1985), 1211–1236.Google Scholar
2. Rickart, C. E., General theory of Banach algebras, The University Series in Higher Mathematics (Van Nostrand, Princeton, N.J., 1960).Google Scholar