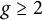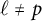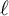1 Introduction
Isogeny graphs are finite graphs associated with elliptic curves, more generally, abelian varieties over finite fields. They have attracted attention not only in arithmetic geometry but also in cryptography since the objects can be used as a building block in a prospective secure encryption scheme. It is believed that finding a path between an arbitrary pair of points is highly intractable in those graphs whereas a relatively short random walk path ends up with a fairly randomized vertex. In this paper, we study a random walk, thus mainly concerning the latter, on the isogeny graphs based on principally polarized superspecial abelian varieties over
![]() $\overline {\mathbb F}_p$
of dimension g at least
$\overline {\mathbb F}_p$
of dimension g at least
![]() $2$
formed by
$2$
formed by
![]() $(\ell )^g$
-isogenies with
$(\ell )^g$
-isogenies with
![]() $p \neq \ell $
for primes p and
$p \neq \ell $
for primes p and
![]() $\ell $
. This is one of natural generalizations beyond the supersingular elliptic curves, the case corresponding to dimension
$\ell $
. This is one of natural generalizations beyond the supersingular elliptic curves, the case corresponding to dimension
![]() $1$
.
$1$
.
1.1 Main theorems
To go into further explanation, we need to fix some notation and the details are left to the relevant sections. Let p be a prime, and let g be a positive integer. Fix an algebraically closed field
![]() $\overline {\mathbb {F}}_p$
of the finite field
$\overline {\mathbb {F}}_p$
of the finite field
![]() $\mathbb {F}_p={\mathbb Z}/p{\mathbb Z}$
. We say an abelian variety over
$\mathbb {F}_p={\mathbb Z}/p{\mathbb Z}$
. We say an abelian variety over
![]() $\overline {\mathbb {F}}_p$
is superspecial if it is isomorphic, as an abelian variety, to a product of a supersingular elliptic curve over
$\overline {\mathbb {F}}_p$
is superspecial if it is isomorphic, as an abelian variety, to a product of a supersingular elliptic curve over
![]() $\overline {\mathbb {F}}_p$
. Let
$\overline {\mathbb {F}}_p$
. Let
![]() $SS_g(p)$
be the set of isomorphism classes of all principally polarized superspecial abelian varieties over
$SS_g(p)$
be the set of isomorphism classes of all principally polarized superspecial abelian varieties over
![]() $\overline {\mathbb {F}}_p$
which are of dimension g. We write
$\overline {\mathbb {F}}_p$
which are of dimension g. We write
![]() $[(A,\mathcal {L})]$
in
$[(A,\mathcal {L})]$
in
![]() $SS_g(p)$
for such a class, where A is a superspecial abelian variety and
$SS_g(p)$
for such a class, where A is a superspecial abelian variety and
![]() $\mathcal {L}$
an endowed principal polarization (an ample line bundle with trivial Euler–Poincaré characteristic).
$\mathcal {L}$
an endowed principal polarization (an ample line bundle with trivial Euler–Poincaré characteristic).
Fix a representative
![]() $(A_0,\mathcal {L}_0)$
in a class of
$(A_0,\mathcal {L}_0)$
in a class of
![]() $SS_g(p)$
and a prime
$SS_g(p)$
and a prime
![]() $\ell \neq p$
. For each
$\ell \neq p$
. For each
![]() $(A,\mathcal {L})$
in a class of
$(A,\mathcal {L})$
in a class of
![]() $SS_g(p)$
, there exists an isogeny
$SS_g(p)$
, there exists an isogeny
![]() $\phi _A:A_0\longrightarrow A$
of
$\phi _A:A_0\longrightarrow A$
of
![]() $\ell $
-power degree such that
$\ell $
-power degree such that
![]() $\mathrm {Ker}(\phi _A)$
is a maximal totally isotropic subspace of
$\mathrm {Ker}(\phi _A)$
is a maximal totally isotropic subspace of
![]() $A[\ell ^n]$
for some
$A[\ell ^n]$
for some
![]() $n\ge 0$
(cf. Theorem 2.6 in Section 2.5 or [Reference Jordan and ZaytmanJZ21, Theorem 34]). We call
$n\ge 0$
(cf. Theorem 2.6 in Section 2.5 or [Reference Jordan and ZaytmanJZ21, Theorem 34]). We call
![]() $\phi _A$
an
$\phi _A$
an
![]() $\ell $
-marking of
$\ell $
-marking of
![]() $(A,\mathcal {L})$
from
$(A,\mathcal {L})$
from
![]() $(A_0,\mathcal {L}_0)$
. If
$(A_0,\mathcal {L}_0)$
. If
![]() $\phi _A$
and
$\phi _A$
and
![]() $\psi _A$
are
$\psi _A$
are
![]() $\ell $
-markings of
$\ell $
-markings of
![]() $(A,\mathcal {L})$
, then
$(A,\mathcal {L})$
, then
![]() $\psi _A = f \circ \phi _A$
for some element f in
$\psi _A = f \circ \phi _A$
for some element f in
where
![]() $\dagger $
stands for the Rosati involution associated with
$\dagger $
stands for the Rosati involution associated with
![]() $\mathcal {L}_0$
(see Proposition 2.3).
$\mathcal {L}_0$
(see Proposition 2.3).
Consider the set of triples
![]() $(A, \mathcal {L}, \phi _A)$
where
$(A, \mathcal {L}, \phi _A)$
where
![]() $[(A, \mathcal {L})]$
in
$[(A, \mathcal {L})]$
in
![]() $SS_g(p)$
and
$SS_g(p)$
and
![]() $\phi _A$
is an
$\phi _A$
is an
![]() $\ell $
-marking of
$\ell $
-marking of
![]() $(A, \mathcal {L})$
. On this set, we define an equivalence relation by saying
$(A, \mathcal {L})$
. On this set, we define an equivalence relation by saying
![]() $(A,\mathcal {L},\phi _A)\sim (A',\mathcal {L}', \phi _A')$
if there exists an isomorphism
$(A,\mathcal {L},\phi _A)\sim (A',\mathcal {L}', \phi _A')$
if there exists an isomorphism
![]() $f : (A, \mathcal {L}) \longrightarrow (A', \mathcal {L}')$
such that
$f : (A, \mathcal {L}) \longrightarrow (A', \mathcal {L}')$
such that
![]() $f \circ \phi _A$
is an
$f \circ \phi _A$
is an
![]() $\ell $
-marking on
$\ell $
-marking on
![]() $(A',\mathcal {L}')$
. Let
$(A',\mathcal {L}')$
. Let
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
be the associated set of equivalence classes.
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
be the associated set of equivalence classes.
We are now ready to define the (
![]() $\ell $
-marked)
$\ell $
-marked)
![]() $(\ell )^g$
-isogeny graph
$(\ell )^g$
-isogeny graph
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
for
${\mathcal G}^{SS}_{g}(\ell ,p)$
for
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
. Let C be a maximal totally isotropic subgroup (or a Lagrangian subspace in other words) of
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
. Let C be a maximal totally isotropic subgroup (or a Lagrangian subspace in other words) of
![]() $A[\ell ]$
. Then the quotient
$A[\ell ]$
. Then the quotient
![]() $A_C=A/C$
yields an object, say
$A_C=A/C$
yields an object, say
![]() $(A_C,\mathcal {L}_C)$
in a class in
$(A_C,\mathcal {L}_C)$
in a class in
![]() $SS_g(p)$
and the natural surjection
$SS_g(p)$
and the natural surjection
![]() $f_C:A\longrightarrow A_C$
is called an
$f_C:A\longrightarrow A_C$
is called an
![]() $(\ell )^g$
-isogeny (see Proposition 2.1 and Definition 2.1). Any
$(\ell )^g$
-isogeny (see Proposition 2.1 and Definition 2.1). Any
![]() $(\ell )^g$
-isogeny between two objects in
$(\ell )^g$
-isogeny between two objects in
![]() $SS_g(p)$
arises in this way. We remark that the number of maximal totally isotropic subgroups
$SS_g(p)$
arises in this way. We remark that the number of maximal totally isotropic subgroups
![]() $A[\ell ]$
is
$A[\ell ]$
is
 $N_g(\ell ):=\displaystyle \prod _{k=1}^g(\ell ^k+1)$
for each A. The (
$N_g(\ell ):=\displaystyle \prod _{k=1}^g(\ell ^k+1)$
for each A. The (
![]() $\ell $
-marked)
$\ell $
-marked)
![]() $(\ell )^g$
-isogeny graph
$(\ell )^g$
-isogeny graph
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
is defined as a directed graph such that:
${\mathcal G}^{SS}_{g}(\ell ,p)$
is defined as a directed graph such that:
-
• the set of vertices
 $V({\mathcal G}^{SS}_{g}(\ell ,p))$
is
$V({\mathcal G}^{SS}_{g}(\ell ,p))$
is
 $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and -
• the set of directed edges between two vertices
 $v_1$
and
$v_1$
and
 $v_2$
is the set of equivalence classes of
$v_2$
is the set of equivalence classes of
 $(\ell )^g$
-isogenies between corresponding principally polarized superspecial abelian varieties commuting with marking isogenies representing
$(\ell )^g$
-isogenies between corresponding principally polarized superspecial abelian varieties commuting with marking isogenies representing
 $v_1$
and
$v_1$
and
 $v_2$
. In other words, if
$v_2$
. In other words, if
 $v_1$
and
$v_1$
and
 $v_2$
correspond to
$v_2$
correspond to
 $[(A_1,\mathcal {L}_1,\phi _{A_1})]$
and
$[(A_1,\mathcal {L}_1,\phi _{A_1})]$
and
 $[(A_2,\mathcal {L}_2,\phi _{A_2})]$
with
$[(A_2,\mathcal {L}_2,\phi _{A_2})]$
with
 $\ell $
-markings
$\ell $
-markings
 $\phi _{A_1}:(A_0,\mathcal {L}_0)\longrightarrow (A_1,\mathcal {L}_1)$
and
$\phi _{A_1}:(A_0,\mathcal {L}_0)\longrightarrow (A_1,\mathcal {L}_1)$
and
 $\phi _{A_2}:(A_0,\mathcal {L}_0)\longrightarrow (A_2,\mathcal {L}_2)$
respectively, then an edge from
$\phi _{A_2}:(A_0,\mathcal {L}_0)\longrightarrow (A_2,\mathcal {L}_2)$
respectively, then an edge from
 $v_1$
to
$v_1$
to
 $v_2$
is an
$v_2$
is an
 $(\ell )^g$
-isogeny
$(\ell )^g$
-isogeny
 $f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
.
$f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
.
Our graph is regular since it has
![]() $N_g(\ell )$
-outgoing edges from each vertex, possibly loops and multiple edges from one to another. The associated random walk operator for
$N_g(\ell )$
-outgoing edges from each vertex, possibly loops and multiple edges from one to another. The associated random walk operator for
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
is self-adjoint with respect to a weighted inner product by the inverse of the order of the reduced automorphism group (see Section 5.2). We define the normalized Laplacian
${\mathcal G}^{SS}_{g}(\ell ,p)$
is self-adjoint with respect to a weighted inner product by the inverse of the order of the reduced automorphism group (see Section 5.2). We define the normalized Laplacian
![]() $\Delta $
on a regular directed multigraph
$\Delta $
on a regular directed multigraph
![]() ${\mathcal G}$
of degree d by
${\mathcal G}$
of degree d by
![]() $\Delta =1-(1/d)M$
for the adjacency matrix M of
$\Delta =1-(1/d)M$
for the adjacency matrix M of
![]() ${\mathcal G}$
. Note that
${\mathcal G}$
. Note that
![]() $\Delta $
has the simple smallest eigenvalue
$\Delta $
has the simple smallest eigenvalue
![]() $0$
provided that the graph is strongly connected, i.e., there exists a directed edge path from any vertex to any other vertex. Our first main result is the following.
$0$
provided that the graph is strongly connected, i.e., there exists a directed edge path from any vertex to any other vertex. Our first main result is the following.
Theorem 1.1 Let
![]() $g \ge 2$
, and let
$g \ge 2$
, and let
![]() $\ell $
be a prime. Then there exists
$\ell $
be a prime. Then there exists
![]() $c_{g,\ell }> 0$
such that for all primes
$c_{g,\ell }> 0$
such that for all primes
![]() $p\neq \ell $
, we have
$p\neq \ell $
, we have
![]() $\lambda _2({\mathcal G}_g^{SS}(\ell ,p)) \ge c_{g,\ell }$
, where
$\lambda _2({\mathcal G}_g^{SS}(\ell ,p)) \ge c_{g,\ell }$
, where
![]() $\lambda _2$
is the second smallest eigenvalue of the normalized Laplacian.
$\lambda _2$
is the second smallest eigenvalue of the normalized Laplacian.
As for the constant in the claim, we may take
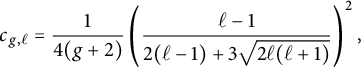 $$\begin{align*}c_{g,\ell}= \frac{1}{4(g+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2, \end{align*}$$
$$\begin{align*}c_{g,\ell}= \frac{1}{4(g+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2, \end{align*}$$
(Corollary 5.5 in Section 5.4). In the course of the proof of Theorem 1.1, we relate
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
to a finite quotient
${\mathcal G}^{SS}_{g}(\ell ,p)$
to a finite quotient
![]() $\Gamma \backslash \mathcal {S}_g$
(see Section 3.3) of the special 1-complex
$\Gamma \backslash \mathcal {S}_g$
(see Section 3.3) of the special 1-complex
![]() $\mathcal {S}_g$
defined in terms of the Bruhat–Tits building for
$\mathcal {S}_g$
defined in terms of the Bruhat–Tits building for
![]() $PGSp_g({\mathbb Q}_\ell )$
(see Theorem 2.6 and Section 4.4). We then move on
$PGSp_g({\mathbb Q}_\ell )$
(see Theorem 2.6 and Section 4.4). We then move on
![]() $\mathcal {S}_g$
to prove the desired property by using Kazhdan’s Property (T) of
$\mathcal {S}_g$
to prove the desired property by using Kazhdan’s Property (T) of
![]() $PGSp_g({\mathbb Q}_\ell )$
for
$PGSp_g({\mathbb Q}_\ell )$
for
![]() $g \ge 2$
.
$g \ge 2$
.
In [Reference Jordan and ZaytmanJZ21], Jordan and Zaytman introduced a big isogeny graph
![]() $Gr_g(\ell , p)$
based on
$Gr_g(\ell , p)$
based on
![]() $SS_g(p)$
. We will show in Sections 2 and 3 that there exist natural identifications
$SS_g(p)$
. We will show in Sections 2 and 3 that there exist natural identifications
which induce natural isomorphisms as graphs between three objects:
-
(1)
 $Gr_g(\ell , p)$
,
$Gr_g(\ell , p)$
, -
(2)
 ${\mathcal G}^{SS}_{g}(\ell ,p)$
, and
${\mathcal G}^{SS}_{g}(\ell ,p)$
, and -
(3) the regular directed graph defined by
 $\Gamma \backslash \mathcal {S}_g$
.
$\Gamma \backslash \mathcal {S}_g$
.
As a consequence, the adjacency matrices of the above three graphs agree with each other. Therefore, the structure of Jordan–Zaytman’s graph
![]() $Gr_g(\ell , p)$
is revealed by our main theorem.
$Gr_g(\ell , p)$
is revealed by our main theorem.
Theorem 1.2 Let p be a prime. For each fixed integer
![]() $g \ge 2$
and for each fixed prime
$g \ge 2$
and for each fixed prime
![]() $\ell \neq p$
, the finite
$\ell \neq p$
, the finite
![]() $N_g(\ell )$
-regular directed multigraph
$N_g(\ell )$
-regular directed multigraph
![]() $Gr_g(\ell , p)$
has the same property as in Theorem 1.1.
$Gr_g(\ell , p)$
has the same property as in Theorem 1.1.
This result implies the rapid mixing property of a lazy version of the walk (see [Reference Florit and SmithFS22, Theorem 4.9]).
In the case when
![]() $g=1$
, it has been shown that if
$g=1$
, it has been shown that if
![]() $p\equiv 1$
mod 12, then
$p\equiv 1$
mod 12, then
![]() $Gr_1(\ell ,p)$
can be defined as a regular undirected graph and it is Ramanujan by Eichler’s theorem via Jacquet–Langlands theory (see [Reference PizerPiz98]). His graphs are regular “undirected” graphs, while in general
$Gr_1(\ell ,p)$
can be defined as a regular undirected graph and it is Ramanujan by Eichler’s theorem via Jacquet–Langlands theory (see [Reference PizerPiz98]). His graphs are regular “undirected” graphs, while in general
![]() $Gr_1(\ell ,p)$
is not necessarily undirected.
$Gr_1(\ell ,p)$
is not necessarily undirected.
Jordan–Zaytman’s graphs
![]() $Gr_g(\ell ,p)$
are useful and fit into the computational implementations (cf. [Reference Castryck, Decru and SmithCDS20, Reference Florit and SmithFS21, Reference Florit and SmithFS22, Reference Katsura, Takashima and GalbraithKT20]) as explained in the next subsection. However, it may be hard to directly obtain the uniform estimation of the eigenvalues of the normalized Laplacian. Our graphs do not, unfortunately, well behave in the computational aspects. However, there is a natural correspondence between
$Gr_g(\ell ,p)$
are useful and fit into the computational implementations (cf. [Reference Castryck, Decru and SmithCDS20, Reference Florit and SmithFS21, Reference Florit and SmithFS22, Reference Katsura, Takashima and GalbraithKT20]) as explained in the next subsection. However, it may be hard to directly obtain the uniform estimation of the eigenvalues of the normalized Laplacian. Our graphs do not, unfortunately, well behave in the computational aspects. However, there is a natural correspondence between
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and
![]() $\mathcal {S}_g$
as explained. A point here is that these two objects have markings from a fixed object, while
$\mathcal {S}_g$
as explained. A point here is that these two objects have markings from a fixed object, while
![]() $SS_g(p)$
does not have it. However, fortunately, there is a natural correspondence between
$SS_g(p)$
does not have it. However, fortunately, there is a natural correspondence between
![]() $SS_g(p)$
and
$SS_g(p)$
and
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
. Then eventually, we can relate
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
. Then eventually, we can relate
![]() $SS_g(p)$
with
$SS_g(p)$
with
![]() $\mathcal {S}_g$
via the intermediate object
$\mathcal {S}_g$
via the intermediate object
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
.
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
.
It seems interesting to consider the moduli space of principal polarized superspecial abelian varieties with a nontrivial-level structure so that the reduced automorphism group of any object is trivial. This will be discussed somewhere else.
1.2 Motivation from isogeny-based cryptography
This study is motivated by construction of cryptographic hash functions from isogeny graphs. Charles, Lauter, and Goren constructed hash functions from random walks on isogeny graphs
![]() $Gr_1(\ell ,p)$
of supersingular elliptic curves [Reference Charles, Lauter and GorenCGL09]. Due to Pizer’s work [Reference PizerPiz90, Reference PizerPiz98], the Ramanujan property of
$Gr_1(\ell ,p)$
of supersingular elliptic curves [Reference Charles, Lauter and GorenCGL09]. Due to Pizer’s work [Reference PizerPiz90, Reference PizerPiz98], the Ramanujan property of
![]() $Gr_1(\ell ,p)$
for
$Gr_1(\ell ,p)$
for
![]() $p\equiv 1\bmod 12$
guarantees efficient mixing processing of these functions (for most precise results, see [Reference Lubetzky and PeresLP16]).
$p\equiv 1\bmod 12$
guarantees efficient mixing processing of these functions (for most precise results, see [Reference Lubetzky and PeresLP16]).
Castryck, Decru, and Smith generalized this construction to design an analogue with genus 2 [Reference Castryck, Decru and SmithCDS20]. To investigate the properties of this function, the study of the big isogeny graphs
![]() $Gr_g(\ell ,p)$
has progressed. For
$Gr_g(\ell ,p)$
has progressed. For
![]() $g=2$
, the classification of possible automorphism groups arising from Jacobians and elliptic product was done by Ibukiyama, Katsura, and Oort [Reference Ibukiyama, Katsura and OortIKO86]. Based on these results, the combinatorial structure of the local neighborhood of each vertex of
$g=2$
, the classification of possible automorphism groups arising from Jacobians and elliptic product was done by Ibukiyama, Katsura, and Oort [Reference Ibukiyama, Katsura and OortIKO86]. Based on these results, the combinatorial structure of the local neighborhood of each vertex of
![]() $Gr_2(2,p)$
is computed in [Reference Florit and SmithFS21, Reference Katsura, Takashima and GalbraithKT20]. Moreover, in [Reference Florit and SmithFS22], they also investigated behavior of random walks on the big isogeny graphs and gave numerical experiments of the mixing rate of
$Gr_2(2,p)$
is computed in [Reference Florit and SmithFS21, Reference Katsura, Takashima and GalbraithKT20]. Moreover, in [Reference Florit and SmithFS22], they also investigated behavior of random walks on the big isogeny graphs and gave numerical experiments of the mixing rate of
![]() $Gr_2(2,p)$
.
$Gr_2(2,p)$
.
However, we know little about expansion properties of these graphs so far. In this paper, good mixing property of the big isogeny graphs
![]() $Gr_g(\ell ,p)$
is shown as a result of proving that the isogeny graphs
$Gr_g(\ell ,p)$
is shown as a result of proving that the isogeny graphs
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
defined in this paper have good expansion property and they are equivalent to the big isogeny graphs
${\mathcal G}^{SS}_{g}(\ell ,p)$
defined in this paper have good expansion property and they are equivalent to the big isogeny graphs
![]() $Gr_g(\ell ,p)$
. Therefore, random walks on the graphs
$Gr_g(\ell ,p)$
. Therefore, random walks on the graphs
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
(and
${\mathcal G}^{SS}_{g}(\ell ,p)$
(and
![]() $Gr_g(\ell ,p)$
) tend to the natural stationary distribution rapidly. This gives an evidence that the big isogeny graphs
$Gr_g(\ell ,p)$
) tend to the natural stationary distribution rapidly. This gives an evidence that the big isogeny graphs
![]() $Gr_g(\ell ,p)$
may be suitable for construction of cryptographic hash functions from superspecial abelian varieties. See Figure 1, the one of examples for the graph
$Gr_g(\ell ,p)$
may be suitable for construction of cryptographic hash functions from superspecial abelian varieties. See Figure 1, the one of examples for the graph
![]() $Gr_g(\ell ,p)$
computed in [Reference Castryck, Decru and SmithCDS20, Reference Katsura, Takashima and GalbraithKT20].
$Gr_g(\ell ,p)$
computed in [Reference Castryck, Decru and SmithCDS20, Reference Katsura, Takashima and GalbraithKT20].
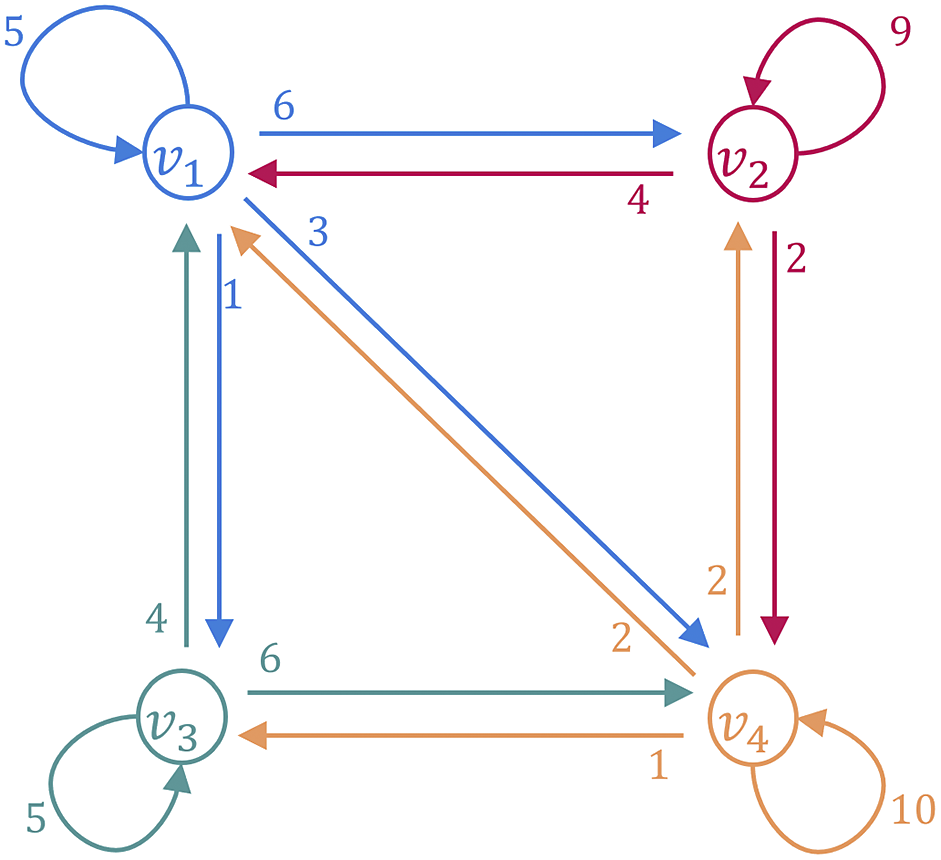
Figure 1: An illustration of
![]() $Gr_2(2,13)$
. The vertices
$Gr_2(2,13)$
. The vertices
![]() $v_1$
,
$v_1$
,
![]() $v_2$
, and
$v_2$
, and
![]() $v_3$
denote the Jacobians of some curves of genus 2. The vertex
$v_3$
denote the Jacobians of some curves of genus 2. The vertex
![]() $v_4$
denotes the product of some supersingular elliptic curves. The number on the side of a directed edge denotes the multiplicity of each edge. For a more detailed illustration, see Section 7.1 of [Reference Katsura, Takashima and GalbraithKT20].
$v_4$
denotes the product of some supersingular elliptic curves. The number on the side of a directed edge denotes the multiplicity of each edge. For a more detailed illustration, see Section 7.1 of [Reference Katsura, Takashima and GalbraithKT20].
1.3 Organization of this paper
In Section 2, we give two interpretations of
![]() $SS_g(p)$
according to works of Ibukiyama–Katsura–Oort–Serre and Jordan–Zaytman. The former is helpful to compute the cardinality of
$SS_g(p)$
according to works of Ibukiyama–Katsura–Oort–Serre and Jordan–Zaytman. The former is helpful to compute the cardinality of
![]() $SS_g(p)$
, while the latter is helpful to make the compatibility of Hecke operators at
$SS_g(p)$
, while the latter is helpful to make the compatibility of Hecke operators at
![]() $\ell $
transparent. As mentioned before, this is a crucial step to apply Property (T) (hence, Theorem 5.4) with our family
$\ell $
transparent. As mentioned before, this is a crucial step to apply Property (T) (hence, Theorem 5.4) with our family
![]() $\{\mathcal {G}^{SS}_{g}(\ell , p)\}_{p\neq \ell }$
. In Section 3, we discuss a comparison between the graph
$\{\mathcal {G}^{SS}_{g}(\ell , p)\}_{p\neq \ell }$
. In Section 3, we discuss a comparison between the graph
![]() ${\mathcal G}_g^{SS}(\ell , p)$
and that of Jordan–Zaytman
${\mathcal G}_g^{SS}(\ell , p)$
and that of Jordan–Zaytman
![]() $Gr_g(\ell , p)$
. In Section 4, we study Bruhat–Tits buildings for symplectic groups. Then, in Section 5, the main result is proved in terms of the terminology in the precedent sections.
$Gr_g(\ell , p)$
. In Section 4, we study Bruhat–Tits buildings for symplectic groups. Then, in Section 5, the main result is proved in terms of the terminology in the precedent sections.
1.4 Notations
Let n be a positive integer, and let
![]() $I_n$
be the identity matrix of size n. Let
$I_n$
be the identity matrix of size n. Let
![]() $GSp_n$
be the generalized symplectic group associated with
$GSp_n$
be the generalized symplectic group associated with
 $J_n= \begin {pmatrix} 0 & I_n \\ -I_n & 0 \end {pmatrix}$
with the similitude
$J_n= \begin {pmatrix} 0 & I_n \\ -I_n & 0 \end {pmatrix}$
with the similitude
![]() $\nu :GSp_n\longrightarrow GL_1$
. Put
$\nu :GSp_n\longrightarrow GL_1$
. Put
![]() $Sp_n:=\mathrm {Ker}(\nu )$
, which is called the symplectic group of rank n. In the sections related to abelian varieties, we put
$Sp_n:=\mathrm {Ker}(\nu )$
, which is called the symplectic group of rank n. In the sections related to abelian varieties, we put
![]() $n=g$
, while we keep n in Sections 4 and 5.
$n=g$
, while we keep n in Sections 4 and 5.
2 Superspecial abelian varieties
In this section, we refer [Reference MumfordMum70] for some general facts of abelian varieties. The purpose here is to understand Theorem 2.10 of [Reference Ibukiyama, Katsura and OortIKO86] in terms of the adelic language which is implicitly given there. Another formulation is also given in terms of
![]() $\ell $
-adic Tate modules (see also Theorem 46 of [Reference Jordan and ZaytmanJZ21] in more general setting). This explains the compatibility of Hecke operators on principally polarized superspecial abelian varieties and the special 1-complex of the Bruhat–Tits building in question. This result will be plugged into the main result in Section 5 to prove Theorem 1.1.
$\ell $
-adic Tate modules (see also Theorem 46 of [Reference Jordan and ZaytmanJZ21] in more general setting). This explains the compatibility of Hecke operators on principally polarized superspecial abelian varieties and the special 1-complex of the Bruhat–Tits building in question. This result will be plugged into the main result in Section 5 to prove Theorem 1.1.
2.1 Superspecial abelian varieties
Let p be a prime number and
![]() $k=\overline {\mathbb {F}}_p$
. Let A be an abelian variety over k of dimension
$k=\overline {\mathbb {F}}_p$
. Let A be an abelian variety over k of dimension
![]() $g>0$
, and we denote by
$g>0$
, and we denote by
![]() $\widehat {A}=\mathrm {Pic}^0(A)$
the dual abelian variety (cf. Section 9 of [Reference MilneMil86]). The abelian variety A is said to be superspecial if A is isomorphic to
$\widehat {A}=\mathrm {Pic}^0(A)$
the dual abelian variety (cf. Section 9 of [Reference MilneMil86]). The abelian variety A is said to be superspecial if A is isomorphic to
![]() $E^g=\overbrace {E\times \cdots \times E}^{g}$
for some supersingular elliptic curve E over k (see Sections 1.6 and 1.7 of [Reference Li and OortLO98] for another definition in terms of a-number). As explained in loc. cit., for any fixed supersingular elliptic curve
$E^g=\overbrace {E\times \cdots \times E}^{g}$
for some supersingular elliptic curve E over k (see Sections 1.6 and 1.7 of [Reference Li and OortLO98] for another definition in terms of a-number). As explained in loc. cit., for any fixed supersingular elliptic curve
![]() $E_0$
over k, every superspecial abelian variety of dimension
$E_0$
over k, every superspecial abelian variety of dimension
![]() $g\ge 2$
is isomorphic to
$g\ge 2$
is isomorphic to
![]() $E^g_0$
. (Here, the assumption
$E^g_0$
. (Here, the assumption
![]() $g\ge 2$
is essential, and indeed, this is not true for
$g\ge 2$
is essential, and indeed, this is not true for
![]() $g=1$
. See also Theorem 4.1 in Chapter V of [Reference SilvermanSil09].) Throughout this section, we fix a supersingular elliptic curve
$g=1$
. See also Theorem 4.1 in Chapter V of [Reference SilvermanSil09].) Throughout this section, we fix a supersingular elliptic curve
![]() $E_0$
.
$E_0$
.
2.2 Principal polarizations
Let A be an abelian variety over
![]() $k=\overline {\mathbb {F}}_p$
. A polarization is a class of the Néron–Severi group
$k=\overline {\mathbb {F}}_p$
. A polarization is a class of the Néron–Severi group
![]() $\mathrm {NS}(A):=\mathrm {Pic}(A)/\mathrm {Pic}^0(A)$
which is represented by an ample line bundle on A. The definition of polarizations here is different from the usual one, but it is equivalent by Remark 13.2 of [Reference MilneMil86] since
$\mathrm {NS}(A):=\mathrm {Pic}(A)/\mathrm {Pic}^0(A)$
which is represented by an ample line bundle on A. The definition of polarizations here is different from the usual one, but it is equivalent by Remark 13.2 of [Reference MilneMil86] since
![]() $k=\overline {\mathbb {F}}_p$
.
$k=\overline {\mathbb {F}}_p$
.
For each ample line bundle
![]() $\mathcal {L}$
, we define an isogeny
$\mathcal {L}$
, we define an isogeny
![]() $\phi _{\mathcal {L}}:A\longrightarrow \widehat {A},\ x\mapsto t^\ast _x(\mathcal {L})\otimes \mathcal {L}^{-1}$
where
$\phi _{\mathcal {L}}:A\longrightarrow \widehat {A},\ x\mapsto t^\ast _x(\mathcal {L})\otimes \mathcal {L}^{-1}$
where
![]() $t_x$
stands for the translation by x and we denote by
$t_x$
stands for the translation by x and we denote by
![]() $t^\ast _x$
its pullback.
$t^\ast _x$
its pullback.
Proposition 2.1 Let
![]() $(A,\mathcal {L})$
be a principally polarized abelian variety over k. Let
$(A,\mathcal {L})$
be a principally polarized abelian variety over k. Let
![]() $\ell $
be a prime number different from p, and let C be a maximal totally isotropic subspace of
$\ell $
be a prime number different from p, and let C be a maximal totally isotropic subspace of
![]() $A[\ell ^n]$
for
$A[\ell ^n]$
for
![]() $n\in {\mathbb Z}_{\ge 0}$
with respect to the Weil pairing associated with
$n\in {\mathbb Z}_{\ge 0}$
with respect to the Weil pairing associated with
![]() $\mathcal {L}$
. Then, there exists an ample line bundle
$\mathcal {L}$
. Then, there exists an ample line bundle
![]() $\mathcal {L}_C$
on the quotient abelian variety
$\mathcal {L}_C$
on the quotient abelian variety
![]() $A_C:=A/C$
which is unique up to isomorphism such that
$A_C:=A/C$
which is unique up to isomorphism such that
![]() $(A_C,\mathcal {L}_{A_C})$
is a principally polarized abelian variety in characteristic p such that
$(A_C,\mathcal {L}_{A_C})$
is a principally polarized abelian variety in characteristic p such that
![]() $f^\ast _C \mathcal {L}_{A_C}=\mathcal {L}^{\otimes \ell ^n}$
where
$f^\ast _C \mathcal {L}_{A_C}=\mathcal {L}^{\otimes \ell ^n}$
where
![]() $f_C:A\longrightarrow A_C$
is the natural surjection.
$f_C:A\longrightarrow A_C$
is the natural surjection.
Proof Notice that
![]() $\mathcal {L}$
is symmetric. The claim follows from (11.25) Proposition of [Reference Edixhoven, van der Geer and MoonenEGM].
$\mathcal {L}$
is symmetric. The claim follows from (11.25) Proposition of [Reference Edixhoven, van der Geer and MoonenEGM].
Definition 2.1 Let
![]() $(A_1,\mathcal {L}_1)$
and
$(A_1,\mathcal {L}_1)$
and
![]() $(A_2,\mathcal {L}_2)$
be two principally polarized abelian varieties in characteristic p. Let
$(A_2,\mathcal {L}_2)$
be two principally polarized abelian varieties in characteristic p. Let
![]() $\ell $
be a prime different from p.
$\ell $
be a prime different from p.
-
(1) An isogeny
 $f:A_1\longrightarrow A_2$
is said to be an
$f:A_1\longrightarrow A_2$
is said to be an
 $(\ell )^g$
-isogeny if
$(\ell )^g$
-isogeny if
 $\mathrm {Ker}(f)$
is a maximal totally isotropic subspace of
$\mathrm {Ker}(f)$
is a maximal totally isotropic subspace of
 $A[\ell ]$
with respect to the Weil pairing associated with
$A[\ell ]$
with respect to the Weil pairing associated with
 $\mathcal {L}_1$
, and
$\mathcal {L}_1$
, and
 $f^\ast \mathcal {L}_2\simeq \mathcal {L}^{\otimes \ell }_1$
.
$f^\ast \mathcal {L}_2\simeq \mathcal {L}^{\otimes \ell }_1$
. -
(2) An isogeny
 $f:A_1\longrightarrow A_2$
is said to be an
$f:A_1\longrightarrow A_2$
is said to be an
 $\ell $
-marking of
$\ell $
-marking of
 $(A_2,\mathcal {L}_2)$
from
$(A_2,\mathcal {L}_2)$
from
 $(A_1,\mathcal {L}_1)$
if
$(A_1,\mathcal {L}_1)$
if
 $f^\ast \mathcal {L}_2=\mathcal {L}^{\otimes \ell ^m}_1$
for some integer
$f^\ast \mathcal {L}_2=\mathcal {L}^{\otimes \ell ^m}_1$
for some integer
 $m\ge 0$
.
$m\ge 0$
.
Proposition 2.2 Keep the notation in Definition 2.1. Let
![]() $f:A_1\longrightarrow A_2$
be an
$f:A_1\longrightarrow A_2$
be an
![]() $\ell $
-marking of
$\ell $
-marking of
![]() $(A_2,\mathcal {L}_2)$
from
$(A_2,\mathcal {L}_2)$
from
![]() $(A_1,\mathcal {L}_1)$
, then there exists an
$(A_1,\mathcal {L}_1)$
, then there exists an
![]() $\ell $
-marking
$\ell $
-marking
![]() $\widetilde {f}:A_2\longrightarrow A_1$
of
$\widetilde {f}:A_2\longrightarrow A_1$
of
![]() $(A_1,\mathcal {L}_1)$
from
$(A_1,\mathcal {L}_1)$
from
![]() $(A_2,\mathcal {L}_2)$
such that
$(A_2,\mathcal {L}_2)$
such that
![]() $f\circ \widetilde {f}=[\ell ^m]_{A_2}$
and
$f\circ \widetilde {f}=[\ell ^m]_{A_2}$
and
![]() $\widetilde {f}\circ f=[\ell ^m]_{A_1}$
for some integer
$\widetilde {f}\circ f=[\ell ^m]_{A_1}$
for some integer
![]() $m\ge 0$
.
$m\ge 0$
.
Proof By Theorem 34 of [Reference Jordan and ZaytmanJZ21], we may assume f is an
![]() $(\ell )^g$
-isogeny. Put
$(\ell )^g$
-isogeny. Put
![]() $C=\mathrm {Ker} f$
. Then
$C=\mathrm {Ker} f$
. Then
![]() $(A_2,\mathcal {L}_2)=(A_{1,C},\mathcal {L}_{A_{1,C}})$
where
$(A_2,\mathcal {L}_2)=(A_{1,C},\mathcal {L}_{A_{1,C}})$
where
![]() $A_{1,C}=A_1/C$
. It is easy to see that
$A_{1,C}=A_1/C$
. It is easy to see that
![]() $D:=A_1[\ell ]/C$
is a maximal totally isotropic subspace of
$D:=A_1[\ell ]/C$
is a maximal totally isotropic subspace of
![]() $A_{1,C}[\ell ]$
with respect to the Weil pairing associated with
$A_{1,C}[\ell ]$
with respect to the Weil pairing associated with
![]() $\mathcal {L}_{A_{1,C}}$
. Therefore, we have an
$\mathcal {L}_{A_{1,C}}$
. Therefore, we have an
![]() $(\ell )^g$
-isogeny
$(\ell )^g$
-isogeny
![]() $\widetilde {f}:A_2\longrightarrow A_{1,C}/D$
. However,
$\widetilde {f}:A_2\longrightarrow A_{1,C}/D$
. However,
![]() $A_{1,C}/D=A/A[\ell ]\simeq A$
and the later isomorphism induces the identification of
$A_{1,C}/D=A/A[\ell ]\simeq A$
and the later isomorphism induces the identification of
![]() $(A_{1,C}/D,\mathcal {L}_D)$
and
$(A_{1,C}/D,\mathcal {L}_D)$
and
![]() $(A_1,\mathcal {L}_1)$
where
$(A_1,\mathcal {L}_1)$
where
![]() $\mathcal {L}_D$
stands for a unique descend of
$\mathcal {L}_D$
stands for a unique descend of
![]() $\mathcal {L}_{A_{1,C}}$
on
$\mathcal {L}_{A_{1,C}}$
on
![]() $A_{1,C}/D$
(see Proposition 2.1). The proportion of f and
$A_{1,C}/D$
(see Proposition 2.1). The proportion of f and
![]() $\widetilde {f}$
is symmetric, and hence we have the claim.
$\widetilde {f}$
is symmetric, and hence we have the claim.
We study the difference of two
![]() $\ell $
-markings. Let us keep the notation in Definition 2.1. By using the principal polarization
$\ell $
-markings. Let us keep the notation in Definition 2.1. By using the principal polarization
![]() $\mathcal {L}_1$
, we define the Rosati-involution
$\mathcal {L}_1$
, we define the Rosati-involution
![]() $\dagger $
on
$\dagger $
on
![]() $\mathrm {End}(A_1)$
by
$\mathrm {End}(A_1)$
by
Notice that
![]() $\dagger $
is an anti-involution.
$\dagger $
is an anti-involution.
Proposition 2.3 Let us still keep the notation in Definition 2.1. Let
![]() $f,h:A_1\longrightarrow A_2$
be two
$f,h:A_1\longrightarrow A_2$
be two
![]() $\ell $
-markings. Then there exists
$\ell $
-markings. Then there exists
![]() $\psi \in \mathrm {End}(A_1)\otimes {\mathbb Z}[1/\ell ]$
such that
$\psi \in \mathrm {End}(A_1)\otimes {\mathbb Z}[1/\ell ]$
such that
![]() $f\circ \psi =h$
and
$f\circ \psi =h$
and
![]() $\psi \circ \psi ^{\dagger }= \psi ^{\dagger }\circ \psi =[\ell ^m]_{A_1}$
for some integer m.
$\psi \circ \psi ^{\dagger }= \psi ^{\dagger }\circ \psi =[\ell ^m]_{A_1}$
for some integer m.
Proof For f, let
![]() $\widetilde {f}:A_2\longrightarrow A_1$
be an
$\widetilde {f}:A_2\longrightarrow A_1$
be an
![]() $(\ell )^g$
-isogeny in Proposition 2.2. Put
$(\ell )^g$
-isogeny in Proposition 2.2. Put
![]() $\psi _1=\widetilde {f}\circ h\in \mathrm {End}(A_1)$
. Then we have, by definition,
$\psi _1=\widetilde {f}\circ h\in \mathrm {End}(A_1)$
. Then we have, by definition,
By [Reference Jordan and ZaytmanJZ21, Theorem 34] and Definition 2.1 that
![]() $\widehat {\widetilde {f}}\circ \phi _{\mathcal {L}_1}\circ \widetilde {f}= \phi _{\mathcal {L}^{\otimes \ell ^{m}}_2}=\ell ^m \phi _{\mathcal {L}_2}$
and
$\widehat {\widetilde {f}}\circ \phi _{\mathcal {L}_1}\circ \widetilde {f}= \phi _{\mathcal {L}^{\otimes \ell ^{m}}_2}=\ell ^m \phi _{\mathcal {L}_2}$
and
![]() $\widehat {h}\circ \phi _{\mathcal {L}_2}\circ h=\phi _{\mathcal {L}^{\otimes \ell ^{m'}}_1}=\ell ^{m'} \phi _{\mathcal {L}_1}$
for some integers
$\widehat {h}\circ \phi _{\mathcal {L}_2}\circ h=\phi _{\mathcal {L}^{\otimes \ell ^{m'}}_1}=\ell ^{m'} \phi _{\mathcal {L}_1}$
for some integers
![]() $m',m\ge 0$
. This yields
$m',m\ge 0$
. This yields
Further,
![]() $f\circ \psi =(f\circ \widetilde {f})\circ h=\ell ^m h$
. Therefore, we may put
$f\circ \psi =(f\circ \widetilde {f})\circ h=\ell ^m h$
. Therefore, we may put
![]() $\psi =\ell ^{-m}\psi _1$
as desired.
$\psi =\ell ^{-m}\psi _1$
as desired.
2.3 Class number of the principal genus for quaternion Hermitian lattices
In this subsection, we refer Section 3.2 of [Reference IbukiyamaIbu20] for the facts and the notation. Let p be a prime number, and let n be a positive integer. Let B be the definite quaternion algebra ramified only at p and
![]() $\infty $
. Let us fix a maximal order
$\infty $
. Let us fix a maximal order
![]() $\mathcal {O}$
of B.
$\mathcal {O}$
of B.
For a commutative ring R, we extend the conjugation on
![]() $\mathcal {O}\subset B$
to
$\mathcal {O}\subset B$
to
![]() $\mathcal {O}\otimes _{\mathbb Z} R$
by
$\mathcal {O}\otimes _{\mathbb Z} R$
by
![]() $\overline {x\otimes r}:=\overline {x}\otimes r$
for each
$\overline {x\otimes r}:=\overline {x}\otimes r$
for each
![]() $x\in \mathcal {O}$
and
$x\in \mathcal {O}$
and
![]() $r\in R$
. Further, for each
$r\in R$
. Further, for each
![]() $\gamma =(\gamma _{ij})\in M_n(\mathcal {O}\otimes _{\mathbb Z} R)$
(the set of
$\gamma =(\gamma _{ij})\in M_n(\mathcal {O}\otimes _{\mathbb Z} R)$
(the set of
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() $\mathcal {O}\otimes _{\mathbb Z} R$
), we define
$\mathcal {O}\otimes _{\mathbb Z} R$
), we define
![]() $\overline {\gamma }:= (\overline {\gamma }_{ij})$
. We define the algebraic group
$\overline {\gamma }:= (\overline {\gamma }_{ij})$
. We define the algebraic group
![]() $G_n$
over
$G_n$
over
![]() ${\mathbb Z}$
which represents the following functor from the category of rings to the category of sets:
${\mathbb Z}$
which represents the following functor from the category of rings to the category of sets:
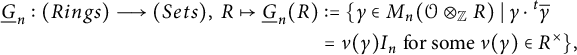 $$ \begin{align*}\underline{G}_n:(Rings)\longrightarrow (Sets),\ R\mapsto\underline{G}_n(R)&:= \{\gamma\in M_n(\mathcal{O}\otimes_{\mathbb Z} R)\ |\ \gamma\cdot {}^t\overline{\gamma}\\ &=\nu(\gamma)I_n\ \text{for some }\nu(\gamma)\in R^\times \},\end{align*} $$
$$ \begin{align*}\underline{G}_n:(Rings)\longrightarrow (Sets),\ R\mapsto\underline{G}_n(R)&:= \{\gamma\in M_n(\mathcal{O}\otimes_{\mathbb Z} R)\ |\ \gamma\cdot {}^t\overline{\gamma}\\ &=\nu(\gamma)I_n\ \text{for some }\nu(\gamma)\in R^\times \},\end{align*} $$
where
![]() $I_n$
stands for the identity matrix of size n. The similitude map
$I_n$
stands for the identity matrix of size n. The similitude map
![]() $\nu :G_n\mapsto GL_1$
is defined by
$\nu :G_n\mapsto GL_1$
is defined by
![]() $\gamma \mapsto \nu (\gamma )$
. Put
$\gamma \mapsto \nu (\gamma )$
. Put
![]() $G^1_n:=\mathrm {Ker}(\nu )$
as an algebraic group. The group scheme
$G^1_n:=\mathrm {Ker}(\nu )$
as an algebraic group. The group scheme
![]() $G_n ($
resp.
$G_n ($
resp.
![]() $G^1_n)$
over
$G^1_n)$
over
![]() ${\mathbb Z}$
is said to be the generalized unitary symplectic group (unitary symplectic group), and it is symbolically denoted by
${\mathbb Z}$
is said to be the generalized unitary symplectic group (unitary symplectic group), and it is symbolically denoted by
![]() $G_n=GUSp_n$
(resp.
$G_n=GUSp_n$
(resp.
![]() $G^1_n=USp_n$
). It is easy to see that
$G^1_n=USp_n$
). It is easy to see that
![]() $G_n({\mathbb R})$
is compact modulo center and
$G_n({\mathbb R})$
is compact modulo center and
![]() $G^1_n({\mathbb R})$
is, in fact, compact, since B is definite. By definition,
$G^1_n({\mathbb R})$
is, in fact, compact, since B is definite. By definition,
![]() $G_n ($
resp.
$G_n ($
resp.
![]() $G^1_n)$
is an inner form of
$G^1_n)$
is an inner form of
![]() $GSp_n$
(resp.
$GSp_n$
(resp.
![]() $Sp_n$
).
$Sp_n$
).
Let
![]() $\mathbb {A}_{\mathbb Q}$
be the ring of adeles of
$\mathbb {A}_{\mathbb Q}$
be the ring of adeles of
![]() ${\mathbb Q}$
, and let
${\mathbb Q}$
, and let
![]() $\mathbb {A}_f$
be the finite part of
$\mathbb {A}_f$
be the finite part of
![]() $\mathbb {A}_{\mathbb Q}$
. For an
$\mathbb {A}_{\mathbb Q}$
. For an
![]() $\mathcal {O}$
-lattice L of
$\mathcal {O}$
-lattice L of
![]() $B^n$
and each rational prime p, put
$B^n$
and each rational prime p, put
![]() $K_p(L):= \{\gamma _p\in G_n({\mathbb Q}_p)\ |\ (L\otimes _{\mathbb Z}{\mathbb Z}_p)\gamma _p=L\otimes _{\mathbb Z}{\mathbb Z}_p\}$
which is an open compact subgroup of
$K_p(L):= \{\gamma _p\in G_n({\mathbb Q}_p)\ |\ (L\otimes _{\mathbb Z}{\mathbb Z}_p)\gamma _p=L\otimes _{\mathbb Z}{\mathbb Z}_p\}$
which is an open compact subgroup of
![]() $G_n({\mathbb Q}_p)$
. Then
$G_n({\mathbb Q}_p)$
. Then
![]() $K(L):=\displaystyle \prod _{p}K_p(L)$
makes up an open compact subgroup of
$K(L):=\displaystyle \prod _{p}K_p(L)$
makes up an open compact subgroup of
![]() $G_n(\mathbb {A}_f)$
.
$G_n(\mathbb {A}_f)$
.
2.4 Ibukiyama–Katsura–Oort–Serre’s result in terms of adelic language
Let us fix a prime p and put
![]() $k=\overline {\mathbb {F}}_p$
. We denote by
$k=\overline {\mathbb {F}}_p$
. We denote by
![]() $SS_g(p)$
the set of all isomorphism classes of principally polarized abelian variety over k of dimension g. Henceforth, we assume
$SS_g(p)$
the set of all isomorphism classes of principally polarized abelian variety over k of dimension g. Henceforth, we assume
![]() $g\ge 2$
. According to [Reference Ibukiyama, Katsura and OortIKO86], we describe
$g\ge 2$
. According to [Reference Ibukiyama, Katsura and OortIKO86], we describe
![]() $SS_g(p)$
in terms of adelic language. Let us first recall the main result in [Reference Ibukiyama, Katsura and OortIKO86].
$SS_g(p)$
in terms of adelic language. Let us first recall the main result in [Reference Ibukiyama, Katsura and OortIKO86].
Theorem 2.4 (Ibukiyama–Katsura–Oort–Serre’s theorem)
There is a one-to-one correspondence between
![]() $SS_g(p)$
and
$SS_g(p)$
and
![]() $K(\mathcal {O}^g)\backslash G_g(\mathbb {A}_f)/G_g({\mathbb Q})$
.
$K(\mathcal {O}^g)\backslash G_g(\mathbb {A}_f)/G_g({\mathbb Q})$
.
We denote by
![]() $Z_{G_g}\simeq GL_1$
the center of
$Z_{G_g}\simeq GL_1$
the center of
![]() $G_g=GUSp_g$
. Recall the open compact subgroup
$G_g=GUSp_g$
. Recall the open compact subgroup
![]() $K(\mathcal {O}^g)=\displaystyle \prod _pK_p(\mathcal {O}^g)$
. For each prime
$K(\mathcal {O}^g)=\displaystyle \prod _pK_p(\mathcal {O}^g)$
. For each prime
![]() $\ell \neq p$
, put
$\ell \neq p$
, put
![]() $K(\mathcal {O}^g)^{(\ell )}=\displaystyle \prod _{p\neq \ell }K_p(\mathcal {O}^g)$
. Clearly,
$K(\mathcal {O}^g)^{(\ell )}=\displaystyle \prod _{p\neq \ell }K_p(\mathcal {O}^g)$
. Clearly,
![]() $K(\mathcal {O}^g)=K(\mathcal {O}^g)^{(\ell )}\times G_g({\mathbb Z}_\ell )$
. We identify
$K(\mathcal {O}^g)=K(\mathcal {O}^g)^{(\ell )}\times G_g({\mathbb Z}_\ell )$
. We identify
![]() $B_\ell =B\otimes _{{\mathbb Q}}{\mathbb Q}_\ell $
(resp.
$B_\ell =B\otimes _{{\mathbb Q}}{\mathbb Q}_\ell $
(resp.
![]() $\mathcal {O}_\ell =\mathcal {O}\otimes _{{\mathbb Z}}{\mathbb Z}_\ell $
) with
$\mathcal {O}_\ell =\mathcal {O}\otimes _{{\mathbb Z}}{\mathbb Z}_\ell $
) with
![]() $M_2({\mathbb Q}_\ell )$
(resp.
$M_2({\mathbb Q}_\ell )$
(resp.
![]() $M_2({\mathbb Z}_\ell )$
). Under this identification, we have
$M_2({\mathbb Z}_\ell )$
). Under this identification, we have
![]() $G_g(R)=GSp_g(R)$
for
$G_g(R)=GSp_g(R)$
for
![]() $R={\mathbb Z}_\ell $
or
$R={\mathbb Z}_\ell $
or
![]() ${\mathbb Q}_\ell $
(cf. Lemma 4 of [Reference GhitzaGhi04]). Therefore, for any subring M of
${\mathbb Q}_\ell $
(cf. Lemma 4 of [Reference GhitzaGhi04]). Therefore, for any subring M of
![]() ${\mathbb Q}_\ell $
,
${\mathbb Q}_\ell $
,
![]() $G_g(M)$
is naturally identified with a subgroup of
$G_g(M)$
is naturally identified with a subgroup of
![]() $G_g({\mathbb Q}_\ell )=GSp_g({\mathbb Q}_\ell )$
under the inclusion
$G_g({\mathbb Q}_\ell )=GSp_g({\mathbb Q}_\ell )$
under the inclusion
![]() $M\subset {\mathbb Q}_\ell $
.
$M\subset {\mathbb Q}_\ell $
.
Proposition 2.5 For each prime
![]() $\ell \neq p$
, there is a one-to-one correspondence between
$\ell \neq p$
, there is a one-to-one correspondence between
![]() $SS_g(p)$
and
$SS_g(p)$
and
![]() $G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
.
$G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
.
Proof For any algebraic closed field F,
![]() $G^1_g(F)=USp_g(F)=Sp_g(F)$
. Since
$G^1_g(F)=USp_g(F)=Sp_g(F)$
. Since
![]() $Sp_g$
is simply connected as a group scheme over
$Sp_g$
is simply connected as a group scheme over
![]() ${\mathbb Z}$
, so is
${\mathbb Z}$
, so is
![]() $G^1_g=USp_g$
. Let
$G^1_g=USp_g$
. Let
![]() $\mathbb {A}^{(\ell )}_f$
be the finite adeles of
$\mathbb {A}^{(\ell )}_f$
be the finite adeles of
![]() ${\mathbb Q}$
outside
${\mathbb Q}$
outside
![]() $\ell $
. By the strong approximation theorem (cf. Theorem 7.12, p.427 in Section 7.4 of [Reference Platonov and RapinchukPR94]) for
$\ell $
. By the strong approximation theorem (cf. Theorem 7.12, p.427 in Section 7.4 of [Reference Platonov and RapinchukPR94]) for
![]() $G^1_g$
with respect to
$G^1_g$
with respect to
![]() $S=\{\infty ,\ell \}$
and using the exact sequence
$S=\{\infty ,\ell \}$
and using the exact sequence
![]() $1\longrightarrow G^1_g\longrightarrow G_g\stackrel {\nu }{\longrightarrow } GL_1\longrightarrow 1,$
we have a decomposition
$1\longrightarrow G^1_g\longrightarrow G_g\stackrel {\nu }{\longrightarrow } GL_1\longrightarrow 1,$
we have a decomposition
Combining Theorem 2.4 with (2.3), we have
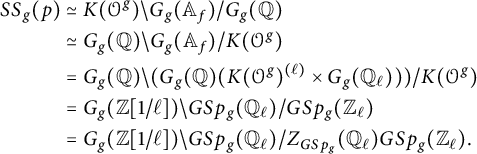 $$ \begin{align} SS_g(p)&\simeq K(\mathcal{O}^g)\backslash G_g(\mathbb{A}_f)/G_g({\mathbb Q}) \nonumber \\ &\simeq G_g({\mathbb Q})\backslash G_g(\mathbb{A}_f)/K(\mathcal{O}^g)\\ &=G_g({\mathbb Q})\backslash (G_g({\mathbb Q})(K(\mathcal{O}^g)^{(\ell)}\times G_g({\mathbb Q}_\ell)))/K(\mathcal{O}^g) \nonumber \\ &=G_g({\mathbb Z}[1/\ell])\backslash GSp_g({\mathbb Q}_\ell)/ GSp_g({\mathbb Z}_\ell) \nonumber \\ &=G_g({\mathbb Z}[1/\ell])\backslash GSp_g({\mathbb Q}_\ell)/Z_{GSp_g}({\mathbb Q}_\ell) GSp_g({\mathbb Z}_\ell). \nonumber \end{align} $$
$$ \begin{align} SS_g(p)&\simeq K(\mathcal{O}^g)\backslash G_g(\mathbb{A}_f)/G_g({\mathbb Q}) \nonumber \\ &\simeq G_g({\mathbb Q})\backslash G_g(\mathbb{A}_f)/K(\mathcal{O}^g)\\ &=G_g({\mathbb Q})\backslash (G_g({\mathbb Q})(K(\mathcal{O}^g)^{(\ell)}\times G_g({\mathbb Q}_\ell)))/K(\mathcal{O}^g) \nonumber \\ &=G_g({\mathbb Z}[1/\ell])\backslash GSp_g({\mathbb Q}_\ell)/ GSp_g({\mathbb Z}_\ell) \nonumber \\ &=G_g({\mathbb Z}[1/\ell])\backslash GSp_g({\mathbb Q}_\ell)/Z_{GSp_g}({\mathbb Q}_\ell) GSp_g({\mathbb Z}_\ell). \nonumber \end{align} $$
We complete the proof.
2.5 Another formulation due to Jordan–Zaytman
Let
![]() $\ell \neq p$
be a prime. Both of
$\ell \neq p$
be a prime. Both of
![]() $SS_g(p)$
and the Bruhat–Tits building
$SS_g(p)$
and the Bruhat–Tits building
![]() $GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
endowed with Hecke theory at
$GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
endowed with Hecke theory at
![]() $\ell $
. However, it is not transparent to see the compatibility of Hecke actions on both sides under the one-to-one correspondence (2.4). To overcome this, due to Jordan and Zaytman [Reference Jordan and ZaytmanJZ21], we use another formulation of
$\ell $
. However, it is not transparent to see the compatibility of Hecke actions on both sides under the one-to-one correspondence (2.4). To overcome this, due to Jordan and Zaytman [Reference Jordan and ZaytmanJZ21], we use another formulation of
![]() $SS_g(p)$
and its connection to
$SS_g(p)$
and its connection to
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
by using
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
by using
![]() $\ell $
-adic Tate modules.
$\ell $
-adic Tate modules.
Pick
![]() $(A,\mathcal {L})$
from a class in
$(A,\mathcal {L})$
from a class in
![]() $SS_g(p)$
. For a positive integer n, let
$SS_g(p)$
. For a positive integer n, let
![]() $A[\ell ^n]:=\{P\in A(\overline {\mathbb {F}}_p)\ |\ \ell ^n P=0_A\}\simeq ({\mathbb Z}/\ell ^n {\mathbb Z})^{\oplus 2g}$
and put
$A[\ell ^n]:=\{P\in A(\overline {\mathbb {F}}_p)\ |\ \ell ^n P=0_A\}\simeq ({\mathbb Z}/\ell ^n {\mathbb Z})^{\oplus 2g}$
and put
![]() $A[\ell ^\infty ]=\displaystyle \bigcup _{n\ge 1}A[\ell ^n]$
. We denote by
$A[\ell ^\infty ]=\displaystyle \bigcup _{n\ge 1}A[\ell ^n]$
. We denote by
![]() $T_\ell (A)$
the
$T_\ell (A)$
the
![]() $\ell $
-adic Tate module and by
$\ell $
-adic Tate module and by
![]() $V_\ell (A):=T_\ell (A)\otimes _{{\mathbb Z}_\ell }{\mathbb Q}_\ell $
the
$V_\ell (A):=T_\ell (A)\otimes _{{\mathbb Z}_\ell }{\mathbb Q}_\ell $
the
![]() $\ell $
-adic rational Tate module (cf. Section 18 of Chapter IV of [Reference MumfordMum70]). Let us define the coefficient ring
$\ell $
-adic rational Tate module (cf. Section 18 of Chapter IV of [Reference MumfordMum70]). Let us define the coefficient ring
![]() $R_V$
to be
$R_V$
to be
![]() ${\mathbb Z}/\ell ^n{\mathbb Z}$
if
${\mathbb Z}/\ell ^n{\mathbb Z}$
if
![]() $V=A[\ell ^n]$
,
$V=A[\ell ^n]$
,
![]() ${\mathbb Z}_\ell $
if
${\mathbb Z}_\ell $
if
![]() $V=T_\ell (A)$
, and
$V=T_\ell (A)$
, and
![]() ${\mathbb Q}_\ell $
if
${\mathbb Q}_\ell $
if
![]() $V=V_\ell (A)$
. The principal polarization
$V=V_\ell (A)$
. The principal polarization
![]() $\phi _{\mathcal {L}}:A\stackrel {\sim }{\longrightarrow }\widehat {A}$
yields
$\phi _{\mathcal {L}}:A\stackrel {\sim }{\longrightarrow }\widehat {A}$
yields
![]() $V\simeq V^\ast =\mathrm {Hom}_{R_V}(V,R_V)$
, and it induces a non-degenerate alternating pairing
$V\simeq V^\ast =\mathrm {Hom}_{R_V}(V,R_V)$
, and it induces a non-degenerate alternating pairing
![]() $\langle \ast ,\ast \rangle :V\times V\longrightarrow R_V$
. Let C be a maximal isotropic subgroup of
$\langle \ast ,\ast \rangle :V\times V\longrightarrow R_V$
. Let C be a maximal isotropic subgroup of
![]() $A[\ell ^n]$
for some
$A[\ell ^n]$
for some
![]() $n\ge 1$
. Consider the exact sequence
$n\ge 1$
. Consider the exact sequence
Then,
![]() $T_C:=\pi ^{-1}(C)$
is a lattice of
$T_C:=\pi ^{-1}(C)$
is a lattice of
![]() $V_\ell (A)$
. The quotient
$V_\ell (A)$
. The quotient
![]() $A_C:=A/C$
is also a superspecial abelian variety and the line bundle
$A_C:=A/C$
is also a superspecial abelian variety and the line bundle
![]() $\mathcal {L}$
is uniquely descend to a principal polarization
$\mathcal {L}$
is uniquely descend to a principal polarization
![]() $\mathcal {L}_C$
on
$\mathcal {L}_C$
on
![]() $A_C$
by Corollary of Theorem 2 in Section 23 of Chapter IV of [Reference MumfordMum70] (see also Proposition 11.25 of [Reference Edixhoven, van der Geer and MoonenEGM] for the uniqueness). Therefore,
$A_C$
by Corollary of Theorem 2 in Section 23 of Chapter IV of [Reference MumfordMum70] (see also Proposition 11.25 of [Reference Edixhoven, van der Geer and MoonenEGM] for the uniqueness). Therefore,
![]() $T_C\simeq T_\ell (A_C)$
has a symplectic
$T_C\simeq T_\ell (A_C)$
has a symplectic
![]() ${\mathbb Z}_\ell $
-basis
${\mathbb Z}_\ell $
-basis
![]() $\{f_{C,i}\}_{i=1}^{2g}\subset {\mathbb Q}^{2g}_\ell $
which means the matrix
$\{f_{C,i}\}_{i=1}^{2g}\subset {\mathbb Q}^{2g}_\ell $
which means the matrix
![]() $P_C:=(f_{C,1},\ldots ,f_{C,2g})\in M_{2g}({\mathbb Q}_\ell )$
belongs to
$P_C:=(f_{C,1},\ldots ,f_{C,2g})\in M_{2g}({\mathbb Q}_\ell )$
belongs to
![]() $GSp_g({\mathbb Q}_\ell )$
. Another choice of a symplectic
$GSp_g({\mathbb Q}_\ell )$
. Another choice of a symplectic
![]() ${\mathbb Z}_\ell $
-basis of
${\mathbb Z}_\ell $
-basis of
![]() $T_C$
yields
$T_C$
yields
![]() $P_C\gamma $
for some
$P_C\gamma $
for some
![]() $\gamma \in GSp_g({\mathbb Z}_\ell )$
. For each
$\gamma \in GSp_g({\mathbb Z}_\ell )$
. For each
![]() $h\in \mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ]$
which is invertible (hence h is an isogeny of degree a power of
$h\in \mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ]$
which is invertible (hence h is an isogeny of degree a power of
![]() $\ell $
), we see easily that
$\ell $
), we see easily that
![]() $P_{h(C)}=h^\ast P_C$
where
$P_{h(C)}=h^\ast P_C$
where
![]() $h^\ast $
is the endomorphism of
$h^\ast $
is the endomorphism of
![]() $V_\ell (A)$
induced from h. In fact, by the functorial property of the pairing (see page 228 of [Reference MumfordMum70]). We identify
$V_\ell (A)$
induced from h. In fact, by the functorial property of the pairing (see page 228 of [Reference MumfordMum70]). We identify
![]() $G_g({\mathbb Z}[1/\ell ])$
with
$G_g({\mathbb Z}[1/\ell ])$
with
under the natural inclusion
![]() $(\mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ])^\times \hookrightarrow \mathrm {Aut}((V_\ell (A),\langle \ast ,\ast \rangle ))=GSp_g({\mathbb Q}_\ell )$
.
$(\mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ])^\times \hookrightarrow \mathrm {Aut}((V_\ell (A),\langle \ast ,\ast \rangle ))=GSp_g({\mathbb Q}_\ell )$
.
Fix
![]() $(A,\mathcal {L})$
in a class of
$(A,\mathcal {L})$
in a class of
![]() $SS_g(p)$
. We introduce the following sets which play an important role in the construction of the isogeny graphs:
$SS_g(p)$
. We introduce the following sets which play an important role in the construction of the isogeny graphs:
and
where
![]() $\phi _B:A\longrightarrow B$
is an
$\phi _B:A\longrightarrow B$
is an
![]() $\ell $
-marking and
$\ell $
-marking and
![]() $ [(B,\mathcal {M},\phi _B)] $
stands for the equivalent class of
$ [(B,\mathcal {M},\phi _B)] $
stands for the equivalent class of
![]() $(B,\mathcal {M},\phi _B)$
. Here, such two objects
$(B,\mathcal {M},\phi _B)$
. Here, such two objects
![]() $(A_1,\mathcal {L}_1,\phi _{A_1})$
and
$(A_1,\mathcal {L}_1,\phi _{A_1})$
and
![]() $(A_2,\mathcal {L}_2,\phi _{A_2})$
are said to be equivalent if there exists an isomorphism
$(A_2,\mathcal {L}_2,\phi _{A_2})$
are said to be equivalent if there exists an isomorphism
![]() $f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
such that
$f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
such that
![]() $f\circ \phi _{A_1}$
and
$f\circ \phi _{A_1}$
and
![]() $\phi _{A_2}$
differ by only an element in
$\phi _{A_2}$
differ by only an element in
![]() $\Gamma (A_1)^\dagger $
. By definition, the natural map from
$\Gamma (A_1)^\dagger $
. By definition, the natural map from
![]() $SS_g(p,\ell ,A,\mathcal {L})$
to
$SS_g(p,\ell ,A,\mathcal {L})$
to
![]() $\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
is surjective, while
$\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
is surjective, while
![]() $\mathrm {Iso}_{\ell ^\infty }(A)$
is included in
$\mathrm {Iso}_{\ell ^\infty }(A)$
is included in
![]() $SS_g(p)$
. With the above observation, we have obtained a map
$SS_g(p)$
. With the above observation, we have obtained a map
We then show a slightly modified version of Jordan–Zaytman’s theorem, Theorem 46 of [Reference Jordan and ZaytmanJZ21] in conjunction with
![]() $SS_g(p,\ell ,A,\mathcal {L})$
.
$SS_g(p,\ell ,A,\mathcal {L})$
.
Theorem 2.6 Fix
![]() $(A,\mathcal {L})$
in a class of
$(A,\mathcal {L})$
in a class of
![]() $SS_g(p)$
. Keep the notation being as above. It holds that
$SS_g(p)$
. Keep the notation being as above. It holds that
![]() $\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})=SS_g(p)$
and the map (2.8) induces a bijection
$\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})=SS_g(p)$
and the map (2.8) induces a bijection
Further, the natural map
![]() $SS_g(p,\ell ,A,\mathcal {L})\longrightarrow \mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
is also bijective.
$SS_g(p,\ell ,A,\mathcal {L})\longrightarrow \mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
is also bijective.
Proof Surjectivity of (2.8) follows in reverse from the construction by using Corollary of Theorem 2 in Section 23 of Chapter IV of [Reference MumfordMum70] to guarantee the existence of a principal polarization. By Proposition 2.5 and
![]() $\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})\subset SS_g(p)$
, we have
$\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})\subset SS_g(p)$
, we have
and it yields first two claims. With a natural surjection
![]() $SS_g(p,\ell ,A, \mathcal {L})\longrightarrow \mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
and (2.8), we have a surjective map
$SS_g(p,\ell ,A, \mathcal {L})\longrightarrow \mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L})$
and (2.8), we have a surjective map
However, by construction and the identification
![]() $(\mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ])^\times = G_g({\mathbb Z}[1/\ell ])$
, two objects of
$(\mathrm {End}(A)\otimes _{\mathbb Z} {\mathbb Z}[1/\ell ])^\times = G_g({\mathbb Z}[1/\ell ])$
, two objects of
![]() $SS_g(p,\ell ,A,\mathcal {L})$
which go to one element in the target differ by only
$SS_g(p,\ell ,A,\mathcal {L})$
which go to one element in the target differ by only
![]() $\ell $
-markings. Therefore, the above map is bijective. Hence,
$\ell $
-markings. Therefore, the above map is bijective. Hence,
![]() $SS_g(p,\ell ,A,\mathcal {L})\stackrel {\sim }{\longrightarrow }\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L}) =SS_g(p)$
.
$SS_g(p,\ell ,A,\mathcal {L})\stackrel {\sim }{\longrightarrow }\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L}) =SS_g(p)$
.
Note that the factor
![]() $Z_{GSp_g}({\mathbb Q}_\ell )\simeq {\mathbb Q}^\times _\ell $
is intentionally inserted in front of
$Z_{GSp_g}({\mathbb Q}_\ell )\simeq {\mathbb Q}^\times _\ell $
is intentionally inserted in front of
![]() $GSp_g({\mathbb Z}_\ell )$
as explained in the proof of Proposition 2.5.
$GSp_g({\mathbb Z}_\ell )$
as explained in the proof of Proposition 2.5.
As a byproduct, we have the following.
Corollary 2.7 Let
![]() $\ell $
be a prime different from p. Let
$\ell $
be a prime different from p. Let
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
is the isogeny graph defined in Section 1. Then,
${\mathcal G}^{SS}_{g}(\ell ,p)$
is the isogeny graph defined in Section 1. Then,
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
is a connected graph.
${\mathcal G}^{SS}_{g}(\ell ,p)$
is a connected graph.
Proof By the proof of Theorem 2.6, we have
![]() $SS_g(p,\ell ,A,\mathcal {L})\stackrel {\sim }{\longrightarrow }\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L}) =SS_g(p)$
for any fixed
$SS_g(p,\ell ,A,\mathcal {L})\stackrel {\sim }{\longrightarrow }\mathrm {Iso}_{\ell ^\infty }(A,\mathcal {L}) =SS_g(p)$
for any fixed
![]() $(A,\mathcal {L})$
in a class of
$(A,\mathcal {L})$
in a class of
![]() $SS_g(p)$
. This means that any two classes are connected by isogenies of degree a power of
$SS_g(p)$
. This means that any two classes are connected by isogenies of degree a power of
![]() $\ell $
and such an isogeny can be written as a composition of some
$\ell $
and such an isogeny can be written as a composition of some
![]() $(\ell )^g$
-isogenies by Theorem 34 of [Reference Jordan and ZaytmanJZ21]. This shows the claim.
$(\ell )^g$
-isogenies by Theorem 34 of [Reference Jordan and ZaytmanJZ21]. This shows the claim.
2.6 The Hecke operator at
 $\ell $
$\ell $
Finally, we discuss a relation of the map (2.8) with the Hecke operator at
![]() $\ell $
. We refer Section 3 in Chapter VII of [Reference Chai and FaltingsCF90] for general facts and Sections 16–19 of [Reference van der GeerGee08] as a reader’s friendly reference. For each prime
$\ell $
. We refer Section 3 in Chapter VII of [Reference Chai and FaltingsCF90] for general facts and Sections 16–19 of [Reference van der GeerGee08] as a reader’s friendly reference. For each prime
![]() $\ell $
different from p and a class
$\ell $
different from p and a class
![]() $[(A,\mathcal {L},\phi _A)]\in SS_g(p,\ell ,A_0,\mathcal {L}_0)$
, we define the (geometric) Hecke correspondences
$[(A,\mathcal {L},\phi _A)]\in SS_g(p,\ell ,A_0,\mathcal {L}_0)$
, we define the (geometric) Hecke correspondences
![]() $T(\ell )^{\mathrm {geo}}_{(A_0,\mathcal {L}_0)}$
at
$T(\ell )^{\mathrm {geo}}_{(A_0,\mathcal {L}_0)}$
at
![]() $\ell $
:
$\ell $
:
 $$ \begin{align} T(\ell)^{\mathrm{geo}}_{(A_0,\mathcal{L}_0)}([(A,\mathcal{L},\phi_A)]):=\sum_{C\subset A[\ell]\atop \text{maximal isotropic}}[(A_C,\mathcal{L}_C,f_C\circ \phi_A)], \end{align} $$
$$ \begin{align} T(\ell)^{\mathrm{geo}}_{(A_0,\mathcal{L}_0)}([(A,\mathcal{L},\phi_A)]):=\sum_{C\subset A[\ell]\atop \text{maximal isotropic}}[(A_C,\mathcal{L}_C,f_C\circ \phi_A)], \end{align} $$
where
![]() $f_C:A\longrightarrow A_C$
is the natural projection. Similarly, we also define the (geometric) Hecke correspondences
$f_C:A\longrightarrow A_C$
is the natural projection. Similarly, we also define the (geometric) Hecke correspondences
![]() $T(\ell )^{\mathrm {geo}}$
at
$T(\ell )^{\mathrm {geo}}$
at
![]() $\ell $
on
$\ell $
on
![]() $SS_g(p)$
:
$SS_g(p)$
:
 $$ \begin{align} T(\ell)^{\mathrm{geo}}([(A,\mathcal{L})]):=\sum_{C\subset A[\ell]\atop \text{maximal isotropic}}[(A_C,\mathcal{L}_C)]. \end{align} $$
$$ \begin{align} T(\ell)^{\mathrm{geo}}([(A,\mathcal{L})]):=\sum_{C\subset A[\ell]\atop \text{maximal isotropic}}[(A_C,\mathcal{L}_C)]. \end{align} $$
Recall
![]() $GSp_g({\mathbb Q}_\ell )=GSp({\mathbb Q}^{2g}_\ell ,\ \langle \ast ,\ast \rangle )$
where
$GSp_g({\mathbb Q}_\ell )=GSp({\mathbb Q}^{2g}_\ell ,\ \langle \ast ,\ast \rangle )$
where
![]() $\langle \ast ,\ast \rangle $
is the standard symplectic pairing on
$\langle \ast ,\ast \rangle $
is the standard symplectic pairing on
![]() ${\mathbb Q}^{2g}_\ell \times {\mathbb Q}^{2g}_\ell $
. Put
${\mathbb Q}^{2g}_\ell \times {\mathbb Q}^{2g}_\ell $
. Put
![]() $V={\mathbb Q}^{2g}_\ell $
. As seen before, each element of
$V={\mathbb Q}^{2g}_\ell $
. As seen before, each element of
![]() $GSp_g({\mathbb Q}_\ell )/GSp_g({\mathbb Z}_\ell )$
can be regarded as a lattice L of V such that
$GSp_g({\mathbb Q}_\ell )/GSp_g({\mathbb Z}_\ell )$
can be regarded as a lattice L of V such that
![]() $\langle \ast ,\ast \rangle _{L\times L}$
gives a
$\langle \ast ,\ast \rangle _{L\times L}$
gives a
![]() ${\mathbb Z}_\ell $
-integral symplectic structure on L. Using this interpretation, each element of
${\mathbb Z}_\ell $
-integral symplectic structure on L. Using this interpretation, each element of
![]() $GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
can be regard as a homothety class
$GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
can be regard as a homothety class
![]() $[L]$
for such an L. For each L being as above, we define the Hecke correspondence on
$[L]$
for such an L. For each L being as above, we define the Hecke correspondence on
![]() $GSp_g({\mathbb Q}_\ell )/GSp_g({\mathbb Z}_\ell )$
at
$GSp_g({\mathbb Q}_\ell )/GSp_g({\mathbb Z}_\ell )$
at
![]() $\ell $
$\ell $
 $$ \begin{align} T(\ell)([L]):=\sum_{L\subset L_1 \subset \ell^{-1}L \atop L_1/L\text{:maximal isotropic}}[L_1], \end{align} $$
$$ \begin{align} T(\ell)([L]):=\sum_{L\subset L_1 \subset \ell^{-1}L \atop L_1/L\text{:maximal isotropic}}[L_1], \end{align} $$
where
![]() $L_1$
runs over all lattice enjoying
$L_1$
runs over all lattice enjoying
![]() $L\subset L_1 \subset \ell ^{-1}L$
as denoted and that
$L\subset L_1 \subset \ell ^{-1}L$
as denoted and that
![]() $L_1/L$
is a maximal isotropic subgroup of
$L_1/L$
is a maximal isotropic subgroup of
![]() $\ell ^{-1}L/L$
with respect to the symplectic pairing
$\ell ^{-1}L/L$
with respect to the symplectic pairing
![]() $\langle \ast ,\ast \rangle _{\ell ^{-1}L/L\times \ell ^{-1}L/L}$
. Clearly, the action of
$\langle \ast ,\ast \rangle _{\ell ^{-1}L/L\times \ell ^{-1}L/L}$
. Clearly, the action of
![]() $G_g({\mathbb Z}[1/\ell ])$
(given by multiplication from the left) on lattices are equivariant under
$G_g({\mathbb Z}[1/\ell ])$
(given by multiplication from the left) on lattices are equivariant under
![]() $T(\ell )$
. Therefore, it also induces a correspondence on
$T(\ell )$
. Therefore, it also induces a correspondence on
![]() $G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
and by abusing notation, we denote it by
$G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell ) GSp_g({\mathbb Z}_\ell )$
and by abusing notation, we denote it by
![]() $T(\ell )$
. For a set X, we write
$T(\ell )$
. For a set X, we write
![]() $\mathrm {Div}(X)_{\mathbb Z}:=\bigoplus _{P\in X}{\mathbb Z} P$
. The identification (2.8) with the bijection
$\mathrm {Div}(X)_{\mathbb Z}:=\bigoplus _{P\in X}{\mathbb Z} P$
. The identification (2.8) with the bijection
yields a bijection
Then we have obtained the following.
Theorem 2.8 The following diagram is commutative:
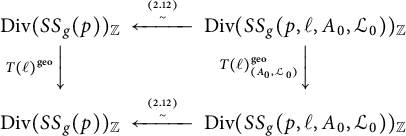

2.7 The Hecke action and automorphisms
In this subsection we describe the behavior of the Hecke action of
![]() $T(\ell )$
on the finite set
$T(\ell )$
on the finite set
in terms of automorphism groups of objects in
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
.
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
.
Put
![]() $\Gamma =G_g({\mathbb Z}[1/\ell ]),\ G=GSp_g({\mathbb Q}_\ell )$
,
$\Gamma =G_g({\mathbb Z}[1/\ell ]),\ G=GSp_g({\mathbb Q}_\ell )$
,
![]() $Z=Z_{GSp_g}({\mathbb Q}_\ell )$
, and
$Z=Z_{GSp_g}({\mathbb Q}_\ell )$
, and
![]() $K=GSp_g({\mathbb Z}_\ell )$
for simplicity. We write
$K=GSp_g({\mathbb Z}_\ell )$
for simplicity. We write
where
![]() $h=h_g(p,1)=|\Gamma \backslash G/ZK|$
. For each
$h=h_g(p,1)=|\Gamma \backslash G/ZK|$
. For each
![]() $i\in \{1,\ldots ,h\}$
, the coset
$i\in \{1,\ldots ,h\}$
, the coset
![]() $\Gamma x_i ZK$
is naturally identified with
$\Gamma x_i ZK$
is naturally identified with
Lemma 2.9 Keep the notation being as above. Let
![]() $(A_i,\mathcal {L}_i,\phi _{A_i})$
be an element in the class corresponding to
$(A_i,\mathcal {L}_i,\phi _{A_i})$
be an element in the class corresponding to
![]() $\Gamma x_i K$
. There is a natural group isomorphism between
$\Gamma x_i K$
. There is a natural group isomorphism between
![]() $\widetilde {\Gamma }_i:=(\Gamma \cap x_i ZK x^{-1}_i)Z/Z$
and
$\widetilde {\Gamma }_i:=(\Gamma \cap x_i ZK x^{-1}_i)Z/Z$
and
![]() $\mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
where
$\mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
where
![]() $\mathrm {Aut}((A_i,\mathcal {L}_i))$
is the group of automorphisms of
$\mathrm {Aut}((A_i,\mathcal {L}_i))$
is the group of automorphisms of
![]() $(A_i,\mathcal {L}_i)$
.
$(A_i,\mathcal {L}_i)$
.
Proof By construction, we have
![]() $T_\ell (A_i)=x_i{\mathbb Z}^{2g}_\ell $
under the inclusion
$T_\ell (A_i)=x_i{\mathbb Z}^{2g}_\ell $
under the inclusion
![]() $T_\ell (A_i)\hookrightarrow V_\ell (A_0){\kern-1pt}={\kern-1pt}{\mathbb Q}^{2g}_\ell $
induced by the
$T_\ell (A_i)\hookrightarrow V_\ell (A_0){\kern-1pt}={\kern-1pt}{\mathbb Q}^{2g}_\ell $
induced by the
![]() $ell$
-marking of
$ell$
-marking of
![]() $(A_i,\mathcal {L}_i)$
. Then the group
$(A_i,\mathcal {L}_i)$
. Then the group
![]() $(\Gamma {\kern-1pt}\cap{\kern-1pt} x_i ZK x^{-1}_i)$
obviously acts on
$(\Gamma {\kern-1pt}\cap{\kern-1pt} x_i ZK x^{-1}_i)$
obviously acts on
![]() $T_\ell (A_i)$
. Thus, we have an injection
$T_\ell (A_i)$
. Thus, we have an injection
![]() $(\Gamma \cap x_i ZK x^{-1}_i)\subset \mathrm {End}(T_\ell (A_i))$
. On the other hand, by Tate’ theorem (cf. Theorem 1 of [Reference TateTate66]),
$(\Gamma \cap x_i ZK x^{-1}_i)\subset \mathrm {End}(T_\ell (A_i))$
. On the other hand, by Tate’ theorem (cf. Theorem 1 of [Reference TateTate66]),
![]() $\mathrm {End}(T_\ell (A_i))\simeq \mathrm {End}(A_i)\otimes _{\mathbb Z}{\mathbb Z}_\ell $
. Hence, we may have
$\mathrm {End}(T_\ell (A_i))\simeq \mathrm {End}(A_i)\otimes _{\mathbb Z}{\mathbb Z}_\ell $
. Hence, we may have
![]() $(\Gamma \cap x_i ZK x^{-1}_i)\subset \mathrm {End}(A_i)\otimes _{\mathbb Z}{\mathbb Z}_\ell $
which is compatible with the identification
$(\Gamma \cap x_i ZK x^{-1}_i)\subset \mathrm {End}(A_i)\otimes _{\mathbb Z}{\mathbb Z}_\ell $
which is compatible with the identification
![]() $\Gamma \subset \Gamma ^\dagger (A_i)$
. Since each element of
$\Gamma \subset \Gamma ^\dagger (A_i)$
. Since each element of
![]() $\Gamma ^\dagger (A_i)$
is an
$\Gamma ^\dagger (A_i)$
is an
![]() $\ell $
-isogeny, it preserves the polarization of
$\ell $
-isogeny, it preserves the polarization of
![]() $A_i$
up to the multiplication by Z. Therefore,
$A_i$
up to the multiplication by Z. Therefore,
![]() $\widetilde {\Gamma }_i\subset \mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
. The opposite inclusion follows by Tate’ theorem again.
$\widetilde {\Gamma }_i\subset \mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
. The opposite inclusion follows by Tate’ theorem again.
Next, we study the image of each element of
![]() $\Gamma \backslash G/K=\Gamma \backslash G/ZK$
under the Hecke action of
$\Gamma \backslash G/K=\Gamma \backslash G/ZK$
under the Hecke action of
![]() $T(\ell )$
. Since
$T(\ell )$
. Since
![]() $T(\ell )$
is defined in terms of lattices (see (2.11)), we define another formulation in terms of elements in G. Let
$T(\ell )$
is defined in terms of lattices (see (2.11)), we define another formulation in terms of elements in G. Let
 $t_\ell :=\mathrm {diag}(\overbrace {1,\ldots ,1}^{g},\overbrace {\ell ,\ldots ,\ell }^{g})\in G$
. We decompose
$t_\ell :=\mathrm {diag}(\overbrace {1,\ldots ,1}^{g},\overbrace {\ell ,\ldots ,\ell }^{g})\in G$
. We decompose
where T is the index set so that
![]() $|T|=N_g(\ell )$
. For each
$|T|=N_g(\ell )$
. For each
![]() $i,j\in \{1,\ldots ,h\}$
, we define
$i,j\in \{1,\ldots ,h\}$
, we define
which is independent of the choice of the representatives
![]() $\{g_t\}_{t\in T}$
. Let
$\{g_t\}_{t\in T}$
. Let
![]() $W(\ell ):=\{g_t ZK\ |\ t\in T\}$
. Then, for each
$W(\ell ):=\{g_t ZK\ |\ t\in T\}$
. Then, for each
![]() $i\in \{1,\ldots ,h\}$
, recall
$i\in \{1,\ldots ,h\}$
, recall
![]() $\widetilde {\Gamma }_i=(\Gamma \cap x_i ZK x^{-1}_i)Z/Z$
, and the finite group
$\widetilde {\Gamma }_i=(\Gamma \cap x_i ZK x^{-1}_i)Z/Z$
, and the finite group
![]() $x_i^{-1}\widetilde {\Gamma }_i x_i\subset KZ/Z$
acts on
$x_i^{-1}\widetilde {\Gamma }_i x_i\subset KZ/Z$
acts on
![]() $W(\ell )$
from the left by multiplication. The action induces the orbit decomposition
$W(\ell )$
from the left by multiplication. The action induces the orbit decomposition
for some subset
![]() $T'\subset T$
.
$T'\subset T$
.
Lemma 2.10 Keep the notation being as above. For each
![]() $i\in \{1,\ldots ,h\}$
and
$i\in \{1,\ldots ,h\}$
and
![]() $t\in T'$
, if
$t\in T'$
, if
![]() $ \Gamma x_i g_t ZK=\Gamma x_j ZK$
for some
$ \Gamma x_i g_t ZK=\Gamma x_j ZK$
for some
![]() $j\in \{1,\ldots ,h\}$
, the stabilizer
$j\in \{1,\ldots ,h\}$
, the stabilizer
![]() $\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_tKZ)$
is isomorphic to a subgroup
$\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_tKZ)$
is isomorphic to a subgroup
![]() $S_i$
of
$S_i$
of
![]() $\widetilde {\Gamma }_j$
.
$\widetilde {\Gamma }_j$
.
Proof By assumption,
![]() $x_j=\gamma x_i g_t z k$
for some
$x_j=\gamma x_i g_t z k$
for some
![]() $\gamma \in \Gamma ,\ z\in Z$
, and
$\gamma \in \Gamma ,\ z\in Z$
, and
![]() $k\in K$
. For each
$k\in K$
. For each
![]() $\alpha Z\in x_i^{-1}\widetilde {\Gamma }_i x_i=(x^{-1}_i\Gamma x_i\cap K)Z/Z$
, let us consider the element
$\alpha Z\in x_i^{-1}\widetilde {\Gamma }_i x_i=(x^{-1}_i\Gamma x_i\cap K)Z/Z$
, let us consider the element
![]() $kg^{-1}_t \alpha g_t k^{-1}Z$
in
$kg^{-1}_t \alpha g_t k^{-1}Z$
in
![]() $G/Z$
. By using
$G/Z$
. By using
![]() $x_j=\gamma x_i g_t z k$
, we see that the element belongs to
$x_j=\gamma x_i g_t z k$
, we see that the element belongs to
![]() $x^{-1}_j \Gamma x_j Z/Z$
. Further, if
$x^{-1}_j \Gamma x_j Z/Z$
. Further, if
![]() $\alpha Z$
is an element of
$\alpha Z$
is an element of
![]() $\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)$
,
$\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)$
,
![]() $kg^{-1}_t \alpha g_t k^{-1}Z$
also belongs to K. Therefore, we have a group homomorphism
$kg^{-1}_t \alpha g_t k^{-1}Z$
also belongs to K. Therefore, we have a group homomorphism
Clearly, this map is injective and we have the claim.
We also study the converse of the correspondence from
![]() $\Gamma x_i g_t ZK$
to
$\Gamma x_i g_t ZK$
to
![]() $\Gamma x_i ZK$
for each
$\Gamma x_i ZK$
for each
![]() $i\in \{1,\ldots ,h\}$
. Clearly,
$i\in \{1,\ldots ,h\}$
. Clearly,
![]() $g^{-1}_tZK\in W(\ell )$
.
$g^{-1}_tZK\in W(\ell )$
.
Lemma 2.11 For each
![]() $i\in \{1,\ldots ,h\}$
and
$i\in \{1,\ldots ,h\}$
and
![]() $t\in T'$
, if
$t\in T'$
, if
![]() $ \Gamma x_i g_t ZK=\Gamma x_j ZK$
for some
$ \Gamma x_i g_t ZK=\Gamma x_j ZK$
for some
![]() ${j\in \{1,\ldots ,h\}}$
, then
${j\in \{1,\ldots ,h\}}$
, then
![]() $|\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)|= |\mathrm {Stab}_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_t KZ)|$
. In particular, it holds
$|\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)|= |\mathrm {Stab}_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_t KZ)|$
. In particular, it holds
Proof As in the proof of the previous lemma, if we write
![]() $x_j=\gamma x_i g_t z k$
, then the conjugation by
$x_j=\gamma x_i g_t z k$
, then the conjugation by
![]() $g_t k^{-1}$
yields the isomorphism from
$g_t k^{-1}$
yields the isomorphism from
![]() $\mathrm {Stab}_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_t KZ)$
to
$\mathrm {Stab}_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_t KZ)$
to
![]() $\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)$
. The claim follows from this.
$\mathrm {Stab}_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_t KZ)$
. The claim follows from this.
Finally, we study the corresponding results in
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
under the identification
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
under the identification
given by Theorem 2.6. We write
Let us fix
![]() $i\in \{1,\ldots ,h\}$
, and we denote by
$i\in \{1,\ldots ,h\}$
, and we denote by
![]() $\mathrm {LG}_i(\ell )=\{C_t\}_{t\in T}$
the set of all totally maximal isotropic subspace of
$\mathrm {LG}_i(\ell )=\{C_t\}_{t\in T}$
the set of all totally maximal isotropic subspace of
![]() $A_i[\ell ]$
with respect to the Weil pairing associated with
$A_i[\ell ]$
with respect to the Weil pairing associated with
![]() $\mathcal {L}_i$
. Here, we use the same index T as
$\mathcal {L}_i$
. Here, we use the same index T as
![]() $W(\ell )$
defined before. Then the group
$W(\ell )$
defined before. Then the group
![]() $\mathrm {RA}_i:=\mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
acts on
$\mathrm {RA}_i:=\mathrm {Aut}((A_i,\mathcal {L}_i))/\{\pm 1\}$
acts on
![]() $\mathrm {LG}(\ell )$
since each element there preserves the polarization. As in (2.16), we also have the decomposition
$\mathrm {LG}(\ell )$
since each element there preserves the polarization. As in (2.16), we also have the decomposition
Suppose
![]() $\Gamma x_i ZK$
corresponds to
$\Gamma x_i ZK$
corresponds to
![]() $w_i=[(A_i,\mathcal {L}_i,\phi _{A_i})]$
under (2.17).
$w_i=[(A_i,\mathcal {L}_i,\phi _{A_i})]$
under (2.17).
Proposition 2.12 Keep the notation being as above. The followings holds.
-
(1) The pullback of
 $\phi _{A_i}$
induces an identification between
$\phi _{A_i}$
induces an identification between
 $\mathrm {LG}_i(\ell )$
and
$\mathrm {LG}_i(\ell )$
and
 $W(\ell )$
.
$W(\ell )$
. -
(2) Suppose
 $C_t\in \mathrm {LG}_i(\ell )$
corresponds to
$C_t\in \mathrm {LG}_i(\ell )$
corresponds to
 $g_tZK\in W(\ell )$
for
$g_tZK\in W(\ell )$
for
 $t\in T$
under the above identification. Let
$t\in T$
under the above identification. Let
 $f_{C_t}:(A_i,\mathcal {L}_{A_i})\longrightarrow (A_{i,C_t},\mathcal {L}_{A_{i,C_t}})$
be the
$f_{C_t}:(A_i,\mathcal {L}_{A_i})\longrightarrow (A_{i,C_t},\mathcal {L}_{A_{i,C_t}})$
be the
 $(\ell )^g$
-isogeny defined by
$(\ell )^g$
-isogeny defined by
 $C_t$
and suppose
$C_t$
and suppose
 $[(A_{i,C_t},\mathcal {L}_{(A_{i,C_t}},f_{C_t}\circ \phi _{A_i})]=w_j$
for some
$[(A_{i,C_t},\mathcal {L}_{(A_{i,C_t}},f_{C_t}\circ \phi _{A_i})]=w_j$
for some
 $j\in \{1,\ldots ,h\}$
and thus
$j\in \{1,\ldots ,h\}$
and thus
 $f_{C_t}$
is regarded as an
$f_{C_t}$
is regarded as an
 $(\ell )^g$
-isogeny from
$(\ell )^g$
-isogeny from
 $(A_i,\mathcal {L}_{A_i})$
to
$(A_i,\mathcal {L}_{A_i})$
to
 $(A_i,\mathcal {L}_{A_j})$
. Let
$(A_i,\mathcal {L}_{A_j})$
. Let
 $\widetilde {f}_{C_t}:(A_i,\mathcal {L}_{A_j})\longrightarrow (A_i,\mathcal {L}_{A_i})$
the
$\widetilde {f}_{C_t}:(A_i,\mathcal {L}_{A_j})\longrightarrow (A_i,\mathcal {L}_{A_i})$
the
 $(\ell )^g$
-isogeny obtained in Proposition 2.2 for
$(\ell )^g$
-isogeny obtained in Proposition 2.2 for
 $f_{C_t}$
. Then it holds:
$f_{C_t}$
. Then it holds:-
• the kernel of
 $\widetilde {f}$
corresponds to
$\widetilde {f}$
corresponds to
 $g^{-1}_tZK$
under the above identification,
$g^{-1}_tZK$
under the above identification, -
•
 $|\mathrm {RA}_i|=|\widetilde {\Gamma }_i|$
,
$|\mathrm {RA}_i|=|\widetilde {\Gamma }_i|$
, -
•
 $|O_{\mathrm {RA}_i}(C_t)|= |O_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_tKZ)|$
,
$|O_{\mathrm {RA}_i}(C_t)|= |O_{x_i^{-1}\widetilde {\Gamma }_i x_i}(g_tKZ)|$
,
 $|O_{\mathrm {RA}_j}(\mathrm {Ker}\widetilde {f}_{C_t})|= |O_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_tKZ)|$
, and
$|O_{\mathrm {RA}_j}(\mathrm {Ker}\widetilde {f}_{C_t})|= |O_{x_j^{-1}\widetilde {\Gamma }_j x_j}(g^{-1}_tKZ)|$
, and -
•
 $|\mathrm {RA}_j|\cdot |O_{\mathrm {RA}_i}(C_t)|= |\mathrm {RA}_i|\cdot |O_{\mathrm {RA}_j}(\mathrm {Ker}\widetilde {f}_{C_t})|$
.
$|\mathrm {RA}_j|\cdot |O_{\mathrm {RA}_i}(C_t)|= |\mathrm {RA}_i|\cdot |O_{\mathrm {RA}_j}(\mathrm {Ker}\widetilde {f}_{C_t})|$
.
-
We remark that the fourth claim of (2) in the above proposition was proved in Lemma 3.2 of [Reference Florit and SmithFS22].
3 A comparison between two graphs
In this section we check, by passing to
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
, that the graph defined by the special 1-complex
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
, that the graph defined by the special 1-complex
![]() $G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell )GSp_g({\mathbb Z}_\ell )$
is naturally identified with Jordan–Zaytman’s big isogeny graph in [Reference Jordan and ZaytmanJZ21].
$G_g({\mathbb Z}[1/\ell ])\backslash GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell )GSp_g({\mathbb Z}_\ell )$
is naturally identified with Jordan–Zaytman’s big isogeny graph in [Reference Jordan and ZaytmanJZ21].
3.1 Jordan–Zaytman’s big isogeny graph
We basically follow the notation in Sections 7.1 and 5.3 of [Reference Jordan and ZaytmanJZ21]. The
![]() $(\ell )^g$
-isogeny (big) graph
$(\ell )^g$
-isogeny (big) graph
![]() $Gr_g(\ell ,p)$
due to Jordan–Zaytman for
$Gr_g(\ell ,p)$
due to Jordan–Zaytman for
![]() $SS_g(p)$
is defined as a directed (regular) graph where:
$SS_g(p)$
is defined as a directed (regular) graph where:
-
• the set of vertices
 $V(Gr_g(\ell ,p))$
is
$V(Gr_g(\ell ,p))$
is
 $SS_g(p)$
and
$SS_g(p)$
and -
• the set of directed edges between two vertices
 $v_1=[(A_1,\mathcal {L}_1)]$
and
$v_1=[(A_1,\mathcal {L}_1)]$
and
 $v_2=[(A_2,\mathcal {L}_2)]$
is the set of equivalence classes of
$v_2=[(A_2,\mathcal {L}_2)]$
is the set of equivalence classes of
 $(\ell )^g$
-isogenies between
$(\ell )^g$
-isogenies between
 $(A_1,\mathcal {L}_1)$
and
$(A_1,\mathcal {L}_1)$
and
 $(A_2,\mathcal {L}_2)$
. Here, two isogenies
$(A_2,\mathcal {L}_2)$
. Here, two isogenies
 $f,h:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
are said to be equivalent if there exist automorphisms
$f,h:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
are said to be equivalent if there exist automorphisms
 $\phi \in \mathrm {Aut}(A_1,\mathcal {L}_1)$
and
$\phi \in \mathrm {Aut}(A_1,\mathcal {L}_1)$
and
 $\psi \in \mathrm {Aut}(A_2,\mathcal {L}_2)$
such that
$\psi \in \mathrm {Aut}(A_2,\mathcal {L}_2)$
such that
 $\psi \circ h=f\circ \phi $
.
$\psi \circ h=f\circ \phi $
.
The case when
![]() $g=1$
is nothing but Pizer’s graph
$g=1$
is nothing but Pizer’s graph
![]() $G(1,p;\ell )$
handled in [Reference PizerPiz90].
$G(1,p;\ell )$
handled in [Reference PizerPiz90].
3.2 The (
 $\ell $
-marked)
$\ell $
-marked)
 $(\ell )^g$
-isogeny graph
$(\ell )^g$
-isogeny graph
Similarly, the (
![]() $\ell $
-marked)
$\ell $
-marked)
![]() $(\ell )^g$
-isogeny graph
$(\ell )^g$
-isogeny graph
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
for
${\mathcal G}^{SS}_{g}(\ell ,p)$
for
![]() $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
is defined as a directed (regular) graph where:
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
is defined as a directed (regular) graph where:
-
• the set of vertices
 $V({\mathcal G}^{SS}_{g}(\ell ,p))$
is
$V({\mathcal G}^{SS}_{g}(\ell ,p))$
is
 $SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and
$SS_g(p,\ell ,A_0,\mathcal {L}_0)$
and -
• the set of edges between two vertices
 $v_1$
and
$v_1$
and
 $v_2$
is the set of equivalence classes of
$v_2$
is the set of equivalence classes of
 $(\ell )^g$
-isogenies between corresponding principally polarized superspecial abelian varieties commuting with marking isogenies representing
$(\ell )^g$
-isogenies between corresponding principally polarized superspecial abelian varieties commuting with marking isogenies representing
 $v_1$
and
$v_1$
and
 $v_2$
under the identification. In other words, if
$v_2$
under the identification. In other words, if
 $v_1$
and
$v_1$
and
 $v_2$
correspond to
$v_2$
correspond to
 $[(A_1,\mathcal {L}_1,\phi _{A_1})]$
and
$[(A_1,\mathcal {L}_1,\phi _{A_1})]$
and
 $[(A_2,\mathcal {L}_2,\phi _{A_2})]$
with
$[(A_2,\mathcal {L}_2,\phi _{A_2})]$
with
 $\ell $
-markings
$\ell $
-markings
 $\phi _{A_1}:(A_0,\mathcal {L}_0)\longrightarrow (A_1,\mathcal {L}_1)$
and
$\phi _{A_1}:(A_0,\mathcal {L}_0)\longrightarrow (A_1,\mathcal {L}_1)$
and
 $\phi _{A_2}:(A_0,\mathcal {L}_0)\longrightarrow (A_2,\mathcal {L}_2)$
respectively, then an edge from
$\phi _{A_2}:(A_0,\mathcal {L}_0)\longrightarrow (A_2,\mathcal {L}_2)$
respectively, then an edge from
 $v_1$
to
$v_1$
to
 $v_2$
is an
$v_2$
is an
 $(\ell )^g$
-isogeny
$(\ell )^g$
-isogeny
 $f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
.
$f:(A_1,\mathcal {L}_1)\longrightarrow (A_2,\mathcal {L}_2)$
.
3.3 The graph defined by the special 1-complex
Put
![]() $\Gamma =G_g({\mathbb Z}[1/\ell ]),\ G=GSp_g({\mathbb Q}_\ell )$
,
$\Gamma =G_g({\mathbb Z}[1/\ell ]),\ G=GSp_g({\mathbb Q}_\ell )$
,
![]() $Z=Z_{GSp_g}({\mathbb Q}_\ell )$
, and
$Z=Z_{GSp_g}({\mathbb Q}_\ell )$
, and
![]() $K=GSp_g({\mathbb Z}_\ell )$
for simplicity. We consider the graph associated with the quotient
$K=GSp_g({\mathbb Z}_\ell )$
for simplicity. We consider the graph associated with the quotient
![]() $\Gamma \backslash \mathcal {S}_g$
where
$\Gamma \backslash \mathcal {S}_g$
where
![]() $\Gamma =G_g({\mathbb Z}[1/\ell ])$
and
$\Gamma =G_g({\mathbb Z}[1/\ell ])$
and
![]() $\mathcal {S}_g=GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell )GSp_g({\mathbb Z}_\ell )$
.
$\mathcal {S}_g=GSp_g({\mathbb Q}_\ell )/Z_{GSp_g}({\mathbb Q}_\ell )GSp_g({\mathbb Z}_\ell )$
.
Two elements
![]() $v_1=\Gamma g_1 ZK$
and
$v_1=\Gamma g_1 ZK$
and
![]() $v_2=\Gamma g_2 ZK$
in
$v_2=\Gamma g_2 ZK$
in
![]() $\Gamma \backslash G/ZK$
said to be adjacent if
$\Gamma \backslash G/ZK$
said to be adjacent if
![]() ${v_2=\Gamma g_1 g_t ZK}$
for some
${v_2=\Gamma g_1 g_t ZK}$
for some
![]() $t \in T$
where
$t \in T$
where
![]() $\{g_t\}_{t\in T}$
is defined in (2.14).
$\{g_t\}_{t\in T}$
is defined in (2.14).
The graph in question, say
![]() $\mathrm {BTQ}^1_g(\ell ,p)$
, is a directed (regular) graph where:
$\mathrm {BTQ}^1_g(\ell ,p)$
, is a directed (regular) graph where:
-
• the set of vertices
 $V(\mathrm {BTQ}^1_g(\ell ,p))$
is
$V(\mathrm {BTQ}^1_g(\ell ,p))$
is
 $\Gamma \backslash G/ZK$
and
$\Gamma \backslash G/ZK$
and -
• the set of directed edges between two vertices
 $v_1=\Gamma g_1 ZK$
and
$v_1=\Gamma g_1 ZK$
and
 $v_2=\Gamma g_2 ZK$
is defined by the adjacency condition in the above sense. Namely, an edge from
$v_2=\Gamma g_2 ZK$
is defined by the adjacency condition in the above sense. Namely, an edge from
 $v_1$
from
$v_1$
from
 $v_2$
is
$v_2$
is
 $g_t$
with
$g_t$
with
 $t\in T$
such that
$t\in T$
such that
 $v_2=\Gamma g_1 g_t ZK$
.
$v_2=\Gamma g_1 g_t ZK$
.
3.4 Comparison theorem
Let us keep the notation in this section. We define
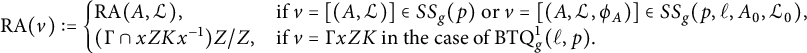 $$ \begin{align*}\mathrm{RA}(v):= \left\{\begin{array}{@{}ll} \mathrm{RA}(A,\mathcal{L}), & \text{if }v=[(A,\mathcal{L})]\in SS_g(p)\text{ or }v=[(A,\mathcal{L},\phi_A)]\in SS_g(p,\ell,A_0,\mathcal{L}_0),\\ (\Gamma\cap x ZK x^{-1})Z/Z, & \text{if }v=\Gamma x ZK\text{ in the case of }\mathrm{BTQ}^1_g(\ell,p). \end{array} \right.\end{align*} $$
$$ \begin{align*}\mathrm{RA}(v):= \left\{\begin{array}{@{}ll} \mathrm{RA}(A,\mathcal{L}), & \text{if }v=[(A,\mathcal{L})]\in SS_g(p)\text{ or }v=[(A,\mathcal{L},\phi_A)]\in SS_g(p,\ell,A_0,\mathcal{L}_0),\\ (\Gamma\cap x ZK x^{-1})Z/Z, & \text{if }v=\Gamma x ZK\text{ in the case of }\mathrm{BTQ}^1_g(\ell,p). \end{array} \right.\end{align*} $$
Further, we also define
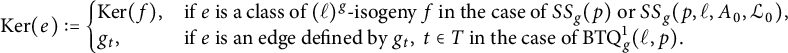 $$ \begin{align*}\mathrm{Ker}(e):= \left\{\begin{array}{@{}ll} \mathrm{Ker}(f), & \text{if }e\text{ is a class of }(\ell)^g\text{-isogeny }f\text{ in the case of }SS_g(p)\text{ or }SS_g(p,\ell,A_0,\mathcal{L}_0),\\ g_t, & \text{if }e\text{ is an edge defined by }g_t,\ t\in T\text{ in the case of }\mathrm{BTQ}^1_g(\ell,p). \end{array} \right.\end{align*} $$
$$ \begin{align*}\mathrm{Ker}(e):= \left\{\begin{array}{@{}ll} \mathrm{Ker}(f), & \text{if }e\text{ is a class of }(\ell)^g\text{-isogeny }f\text{ in the case of }SS_g(p)\text{ or }SS_g(p,\ell,A_0,\mathcal{L}_0),\\ g_t, & \text{if }e\text{ is an edge defined by }g_t,\ t\in T\text{ in the case of }\mathrm{BTQ}^1_g(\ell,p). \end{array} \right.\end{align*} $$
We will prove the following comparison theorem which plays an important role in our study.
Theorem 3.1 The identifications (2.12) and (2.13) induce the following graph isomorphisms:
Further, the following properties are preserved under the isomorphisms:
-
• The Hecke action of
 $T(\ell )^{\mathrm {geo}},\ T(\ell )^{\mathrm {geo}}_{(A_0,\mathcal {L}_0)}$
, or
$T(\ell )^{\mathrm {geo}},\ T(\ell )^{\mathrm {geo}}_{(A_0,\mathcal {L}_0)}$
, or
 $T(\ell )$
on each set of the vertices defines
$T(\ell )$
on each set of the vertices defines
 $N_g(\ell )$
-neighbors of a given vertex.
$N_g(\ell )$
-neighbors of a given vertex. -
• Each edge e from
 $v_1$
to
$v_1$
to
 $v_2$
has an opposite
$v_2$
has an opposite
 $\widehat {e}$
such that
$\widehat {e}$
such that  $$ \begin{align*}|\mathrm{RA}(v_2)|\cdot |O_{\mathrm{RA}(v_1)}(\mathrm{Ker}(e))|=|\mathrm{RA}(v_1)|\cdot |O_{\mathrm{RA}(v_2)}(\mathrm{Ker}(\widehat{e}))|.\end{align*} $$
$$ \begin{align*}|\mathrm{RA}(v_2)|\cdot |O_{\mathrm{RA}(v_1)}(\mathrm{Ker}(e))|=|\mathrm{RA}(v_1)|\cdot |O_{\mathrm{RA}(v_2)}(\mathrm{Ker}(\widehat{e}))|.\end{align*} $$
Proof As in the claim already, the identifications between the sets of vertices are given by (2.12) and (2.13). The compatibility of the Hecke operators follows from Theorem 2.8, and this yields the first property in the latter claim. The remaining formula follows from Proposition 2.12.
Corollary 3.2 Keep the notation being as above. The random walk matrices for
![]() $Gr_g(\ell ,p),\ {\mathcal G}^{SS}_{g}(\ell ,p)$
, and
$Gr_g(\ell ,p),\ {\mathcal G}^{SS}_{g}(\ell ,p)$
, and
![]() $\mathrm {BTQ}^1_g(\ell ,p)$
coincide each other.
$\mathrm {BTQ}^1_g(\ell ,p)$
coincide each other.
We remark that Theorem 2.8 is insufficient to prove the above corollary, while Theorem 3.1 tells us more finer information for the relation of the reduced automorphisms and the multiplicity of each edge.
Remark 3.3 As shown in Theorem 3.1 or Section 3 of [Reference Florit and SmithFS22], the group of reduced automorphisms gives a finer structure of its orbit of a given Lagrangian subspace defining an
![]() $(\ell )^g$
-isogeny. The edges in Figure 1 can be more precise as in the figure in 7A, page 297 of [Reference Katsura, Takashima and GalbraithKT20].
$(\ell )^g$
-isogeny. The edges in Figure 1 can be more precise as in the figure in 7A, page 297 of [Reference Katsura, Takashima and GalbraithKT20].
4 Bruhat–Tits buildings for symplectic groups
In this and the following chapter, we introduce a more general framework than the case to which we apply. The purpose is to simplify the notations and to indicate that the methods we use are applicable in a wider context. The reader may assume that
![]() $F={\mathbb Q}_\ell $
and
$F={\mathbb Q}_\ell $
and
![]() $\varpi =\ell $
in the following discussion.
$\varpi =\ell $
in the following discussion.
4.1 Symplectic groups revisited for the buildings
Let F be a non-archimedean local field of characteristic different from
![]() $2$
, and let
$2$
, and let
![]() $\mathit {O}$
be the ring of integers. We fix a uniformizer
$\mathit {O}$
be the ring of integers. We fix a uniformizer
![]() $\varpi $
and identify the residue field
$\varpi $
and identify the residue field
![]() $\mathit {O}/\varpi \mathit {O}$
with a finite field
$\mathit {O}/\varpi \mathit {O}$
with a finite field
![]() ${\mathbb F}_q$
of order q. Further, we denote by
${\mathbb F}_q$
of order q. Further, we denote by
![]() $F^\times $
and
$F^\times $
and
![]() $\mathit {O}^\times $
the multiplicative groups in F and
$\mathit {O}^\times $
the multiplicative groups in F and
![]() $\mathit {O}$
, respectively. Let
$\mathit {O}$
, respectively. Let
![]() $\mathrm {ord}_\varpi $
be a discrete valuation in F, normalized so that
$\mathrm {ord}_\varpi $
be a discrete valuation in F, normalized so that
![]() $\mathrm {ord}_\varpi (F^\times )={\mathbb Z}$
. For example, we consider the
$\mathrm {ord}_\varpi (F^\times )={\mathbb Z}$
. For example, we consider the
![]() $\ell $
-adic field
$\ell $
-adic field
![]() ${\mathbb Q}_\ell $
for a prime
${\mathbb Q}_\ell $
for a prime
![]() $\ell $
with the ring of integers
$\ell $
with the ring of integers
![]() ${\mathbb Z}_\ell $
, where
${\mathbb Z}_\ell $
, where
![]() $\ell $
is a uniformizer and the residue field is
$\ell $
is a uniformizer and the residue field is
![]() ${\mathbb F}_\ell ={\mathbb Z}/\ell {\mathbb Z}$
.
${\mathbb F}_\ell ={\mathbb Z}/\ell {\mathbb Z}$
.
For a positive integer n, let
![]() $V:=F^{2n}$
be the symplectic space over F equipped with the standard symplectic pairing
$V:=F^{2n}$
be the symplectic space over F equipped with the standard symplectic pairing
![]() $\langle \ast , \ast \rangle $
defined by
$\langle \ast , \ast \rangle $
defined by
![]() $\langle v, w\rangle =\,{}^{t}v J_n w$
for
$\langle v, w\rangle =\,{}^{t}v J_n w$
for
![]() $v, w \in F^{2n}$
. For V, there exists a basis
$v, w \in F^{2n}$
. For V, there exists a basis
![]() $\{v_1, \dots , v_n, w_1, \dots , w_n\}$
such that
$\{v_1, \dots , v_n, w_1, \dots , w_n\}$
such that
![]() $\langle v_i, w_j\rangle =\delta _{i j}$
and
$\langle v_i, w_j\rangle =\delta _{i j}$
and
![]() $\langle v_i, v_j\rangle =\langle w_i, w_j\rangle =0$
for all
$\langle v_i, v_j\rangle =\langle w_i, w_j\rangle =0$
for all
![]() $i, j=1, \dots , n$
, where
$i, j=1, \dots , n$
, where
![]() $\delta _{ij}$
equals
$\delta _{ij}$
equals
![]() $1$
if
$1$
if
![]() $i=j$
and
$i=j$
and
![]() $0$
if
$0$
if
![]() $i \neq j$
, and we call it a symplectic basis of
$i \neq j$
, and we call it a symplectic basis of
![]() $(V, \langle \ast , \ast \rangle )$
. Each choice of a symplectic basis yields an isomorphism between the isometry group and
$(V, \langle \ast , \ast \rangle )$
. Each choice of a symplectic basis yields an isomorphism between the isometry group and
![]() $Sp_n(F)$
.
$Sp_n(F)$
.
Note that the following elements are in
![]() $GSp_n(F)$
:
$GSp_n(F)$
:
 $$\begin{align*}t_\lambda:=\mathrm{diag}(1, \dots, 1, \lambda, \dots, \lambda)= \left( \begin{array}{cc} I_n & 0\\ 0 & \lambda I_n \end{array} \right) \quad \text{for }\lambda \in F^\times. \end{align*}$$
$$\begin{align*}t_\lambda:=\mathrm{diag}(1, \dots, 1, \lambda, \dots, \lambda)= \left( \begin{array}{cc} I_n & 0\\ 0 & \lambda I_n \end{array} \right) \quad \text{for }\lambda \in F^\times. \end{align*}$$
In the subsequent sections, we consider the projectivized groups: let
![]() $PSp_n(F)$
and
$PSp_n(F)$
and
![]() $PGSp_n(F)$
be the groups
$PGSp_n(F)$
be the groups
![]() $Sp_n(F)$
and
$Sp_n(F)$
and
![]() $GSp_n(F)$
modulo the centers, respectively. If we naturally identify
$GSp_n(F)$
modulo the centers, respectively. If we naturally identify
![]() $PSp_n(F)$
with a normal subgroup of
$PSp_n(F)$
with a normal subgroup of
![]() $PGSp_n(F)$
, then the quotient group
$PGSp_n(F)$
, then the quotient group
![]() $PGSp_n(F)/PSp_n(F)$
is isomorphic to
$PGSp_n(F)/PSp_n(F)$
is isomorphic to
![]() $({\mathbb Z}/2{\mathbb Z})\times \mathit {O}^\times $
, which is generated by the images of
$({\mathbb Z}/2{\mathbb Z})\times \mathit {O}^\times $
, which is generated by the images of
![]() $t_\lambda =\mathrm {diag}(1, \dots , 1, \lambda , \dots , \lambda )$
for
$t_\lambda =\mathrm {diag}(1, \dots , 1, \lambda , \dots , \lambda )$
for
![]() $\lambda \in \varpi \mathit { O}^\times $
. Similarly, letting
$\lambda \in \varpi \mathit { O}^\times $
. Similarly, letting
![]() $PSp_n(\mathit {O})$
and
$PSp_n(\mathit {O})$
and
![]() $PGSp_n(\mathit {O})$
be the groups
$PGSp_n(\mathit {O})$
be the groups
![]() $Sp_n(\mathit {O})$
and
$Sp_n(\mathit {O})$
and
![]() $GSp_n(\mathit {O})$
modulo the centers, respectively, we consider
$GSp_n(\mathit {O})$
modulo the centers, respectively, we consider
![]() $PSp_n(\mathit {O})$
as a subgroup in
$PSp_n(\mathit {O})$
as a subgroup in
![]() $PGSp_n(\mathit {O})$
.
$PGSp_n(\mathit {O})$
.
4.2 Bruhat–Tits building: the construction
Let
![]() $(V, \langle \ast , \ast \rangle )$
be a symplectic space over F of dimension
$(V, \langle \ast , \ast \rangle )$
be a symplectic space over F of dimension
![]() $2n$
. We define a lattice
$2n$
. We define a lattice
![]() $\Lambda $
in V as a free
$\Lambda $
in V as a free
![]() $\mathit {O}$
-module of rank
$\mathit {O}$
-module of rank
![]() $2n$
. Note that if
$2n$
. Note that if
![]() $\Lambda $
is a lattice, then
$\Lambda $
is a lattice, then
![]() $\Lambda /\varpi \Lambda $
is a vector space over
$\Lambda /\varpi \Lambda $
is a vector space over
![]() ${\mathbb F}_q$
of dimension
${\mathbb F}_q$
of dimension
![]() $2n$
. We say that a lattice
$2n$
. We say that a lattice
![]() $\Lambda $
is primitive if
$\Lambda $
is primitive if
![]() $\langle \Lambda , \Lambda \rangle \subseteq \mathit {O}$
where
$\langle \Lambda , \Lambda \rangle \subseteq \mathit {O}$
where
![]() $\langle \Lambda , \Lambda \rangle :=\{\langle v, w\rangle \mid v, w \in \Lambda \}$
, and
$\langle \Lambda , \Lambda \rangle :=\{\langle v, w\rangle \mid v, w \in \Lambda \}$
, and
![]() $\langle \ast , \ast \rangle $
induces a non-degenerate alternating form on
$\langle \ast , \ast \rangle $
induces a non-degenerate alternating form on
![]() $\Lambda /\varpi \Lambda $
over
$\Lambda /\varpi \Lambda $
over
![]() ${\mathbb F}_q$
.
${\mathbb F}_q$
.
Let
![]() $\Lambda _i$
for
$\Lambda _i$
for
![]() $i=1, 2$
be lattices in V, and we say that they are homothetic if
$i=1, 2$
be lattices in V, and we say that they are homothetic if
![]() ${\Lambda _1 =\alpha \Lambda _2}$
for some
${\Lambda _1 =\alpha \Lambda _2}$
for some
![]() $\alpha \in F^\times $
. This defines an equivalence relation in the set of lattices in V. We denote the homothety class of a lattice
$\alpha \in F^\times $
. This defines an equivalence relation in the set of lattices in V. We denote the homothety class of a lattice
![]() $\Lambda $
by
$\Lambda $
by
![]() $[\Lambda ]$
. Let us define the set
$[\Lambda ]$
. Let us define the set
![]() ${\mathbb L}_n$
of homothety classes
${\mathbb L}_n$
of homothety classes
![]() $[\Lambda ]$
of lattices such that there exist a representative
$[\Lambda ]$
of lattices such that there exist a representative
![]() $\Lambda $
of
$\Lambda $
of
![]() $[\Lambda ]$
and a primitive lattice
$[\Lambda ]$
and a primitive lattice
![]() $\Lambda _0$
satisfying that
$\Lambda _0$
satisfying that
![]() $\varpi \Lambda _0 \subseteq \Lambda \subseteq \Lambda _0$
and
$\varpi \Lambda _0 \subseteq \Lambda \subseteq \Lambda _0$
and
![]() $\langle \Lambda , \Lambda \rangle \subseteq \varpi \mathit {O}$
. By the definition, if
$\langle \Lambda , \Lambda \rangle \subseteq \varpi \mathit {O}$
. By the definition, if
![]() $[\Lambda ] \in {\mathbb L}_n$
, then a representative
$[\Lambda ] \in {\mathbb L}_n$
, then a representative
![]() $\Lambda $
yields a subspace
$\Lambda $
yields a subspace
![]() $\Lambda /\varpi \Lambda _0$
of
$\Lambda /\varpi \Lambda _0$
of
![]() $\Lambda _0/\varpi \Lambda _0$
with some primitive lattice
$\Lambda _0/\varpi \Lambda _0$
with some primitive lattice
![]() $\Lambda _0$
such that it is totally isotropic, i.e., the induced non-degenerate alternating form
$\Lambda _0$
such that it is totally isotropic, i.e., the induced non-degenerate alternating form
![]() $\langle \ast , \ast \rangle $
vanishes on
$\langle \ast , \ast \rangle $
vanishes on
![]() $\Lambda /\varpi \Lambda _0$
in
$\Lambda /\varpi \Lambda _0$
in
![]() $\Lambda _0/\varpi \Lambda _0$
. Further, we define the incidence relation in
$\Lambda _0/\varpi \Lambda _0$
. Further, we define the incidence relation in
![]() ${\mathbb L}_n$
and denote by
${\mathbb L}_n$
and denote by
![]() $[\Lambda _1] \sim [\Lambda _2]$
for two distinct homothety classes if there exist representatives
$[\Lambda _1] \sim [\Lambda _2]$
for two distinct homothety classes if there exist representatives
![]() $\Lambda _i$
of
$\Lambda _i$
of
![]() $[\Lambda _i]$
for
$[\Lambda _i]$
for
![]() $i=1, 2$
and a primitive lattice
$i=1, 2$
and a primitive lattice
![]() $\Lambda _0$
such that
$\Lambda _0$
such that
![]() $\varpi \Lambda _0 \subseteq \Lambda _i \subseteq \Lambda _0$
for
$\varpi \Lambda _0 \subseteq \Lambda _i \subseteq \Lambda _0$
for
![]() $i=1, 2$
, and either
$i=1, 2$
, and either
![]() $\Lambda _1 \subseteq \Lambda _2$
or
$\Lambda _1 \subseteq \Lambda _2$
or
![]() $\Lambda _2 \subseteq \Lambda _1$
holds.
$\Lambda _2 \subseteq \Lambda _1$
holds.
The Bruhat–Tits building
![]() ${\mathcal B}_n$
(in short, building) for the group
${\mathcal B}_n$
(in short, building) for the group
![]() $PGSp_n(F)$
(or
$PGSp_n(F)$
(or
![]() $Sp_n(F)$
) is the clique complex whose set of vertices
$Sp_n(F)$
) is the clique complex whose set of vertices
![]() $\mathrm {Ver}({\mathcal B}_n)$
is
$\mathrm {Ver}({\mathcal B}_n)$
is
![]() ${\mathbb L}_n$
, i.e.,
${\mathbb L}_n$
, i.e.,
![]() $\sigma \subset \mathrm {Ver}({\mathcal B}_n)$
defines a simplex if any distinct vertices in
$\sigma \subset \mathrm {Ver}({\mathcal B}_n)$
defines a simplex if any distinct vertices in
![]() $\sigma $
are incident. The building
$\sigma $
are incident. The building
![]() ${\mathcal B}_n$
is a simplicial complex of dimension n; note that each chamber (i.e., a simplex of maximal dimension)
${\mathcal B}_n$
is a simplicial complex of dimension n; note that each chamber (i.e., a simplex of maximal dimension)
![]() $[\Lambda _0], [\Lambda _1], \dots , [\Lambda _n]$
corresponds to a sequence of lattices
$[\Lambda _0], [\Lambda _1], \dots , [\Lambda _n]$
corresponds to a sequence of lattices
![]() $\Lambda _0 \subseteq \Lambda _1 \subseteq \cdots \subseteq \Lambda _n \subseteq \varpi ^{-1}\Lambda _0$
, where
$\Lambda _0 \subseteq \Lambda _1 \subseteq \cdots \subseteq \Lambda _n \subseteq \varpi ^{-1}\Lambda _0$
, where
![]() $\varpi ^{-1}\Lambda _0$
is primitive, such that
$\varpi ^{-1}\Lambda _0$
is primitive, such that
forms a complete flag of a maximal totally isotropic subspace
![]() $\Lambda _n/\Lambda _0$
in
$\Lambda _n/\Lambda _0$
in
![]() $\varpi ^{-1}\Lambda _0/\Lambda _0$
over
$\varpi ^{-1}\Lambda _0/\Lambda _0$
over
![]() ${\mathbb F}_q$
.
${\mathbb F}_q$
.
The group
![]() $Sp_n(F)$
acts on
$Sp_n(F)$
acts on
![]() ${\mathcal B}_n$
as simplicial automorphisms: let us fix a symplectic basis
${\mathcal B}_n$
as simplicial automorphisms: let us fix a symplectic basis
![]() $\{v_1, \dots , v_n, w_1, \dots , w_n\}$
of
$\{v_1, \dots , v_n, w_1, \dots , w_n\}$
of
![]() $(V, \langle \ast , \ast \rangle )$
, which we identify with the standard symplectic space over F. Then the action is defined by
$(V, \langle \ast , \ast \rangle )$
, which we identify with the standard symplectic space over F. Then the action is defined by
![]() $[\Lambda ] \mapsto [M \Lambda ]$
for
$[\Lambda ] \mapsto [M \Lambda ]$
for
![]() $[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
and
$[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
and
![]() $M \in Sp_n(F)$
, and this action is simplicial since it preserves the incidence relation. Moreover, this yields the action of the projectivized group
$M \in Sp_n(F)$
, and this action is simplicial since it preserves the incidence relation. Moreover, this yields the action of the projectivized group
![]() $PSp_n(F)$
on
$PSp_n(F)$
on
![]() ${\mathcal B}_n$
.
${\mathcal B}_n$
.
We define the label (or, color) on the set of vertices
![]() $\mathrm {Ver}({\mathcal B}_n)$
. For any lattice
$\mathrm {Ver}({\mathcal B}_n)$
. For any lattice
![]() $\Lambda $
, there exists some
$\Lambda $
, there exists some
![]() $\gamma \in GL_{2n}(F)$
such that
$\gamma \in GL_{2n}(F)$
such that
![]() $\gamma u_1, \dots , \gamma w_n$
form an
$\gamma u_1, \dots , \gamma w_n$
form an
![]() $\mathit {O}$
-basis of
$\mathit {O}$
-basis of
![]() $\Lambda $
. Let
$\Lambda $
. Let
Note that this depends only on the homothety class of
![]() $\Lambda $
since
$\Lambda $
since
![]() $\det (\alpha \gamma )=\alpha ^{2n}\det (\gamma )$
for
$\det (\alpha \gamma )=\alpha ^{2n}\det (\gamma )$
for
![]() $\alpha \in F^\times $
and for
$\alpha \in F^\times $
and for
![]() $\gamma \in GL_{2n}(F)$
, and
$\gamma \in GL_{2n}(F)$
, and
![]() $\det \gamma \in \mathit {O}^\times $
for
$\det \gamma \in \mathit {O}^\times $
for
![]() $\gamma \in GL_{2n}(\mathit {O})$
. Hence, the function
$\gamma \in GL_{2n}(\mathit {O})$
. Hence, the function
![]() $\mathbf {lab}_n:\mathrm {Ver}({\mathcal B}_n) \to {\mathbb Z}/2n{\mathbb Z}$
is well defined and we call
$\mathbf {lab}_n:\mathrm {Ver}({\mathcal B}_n) \to {\mathbb Z}/2n{\mathbb Z}$
is well defined and we call
![]() $\mathbf {lab}_n[\Lambda ]$
the label of a vertex
$\mathbf {lab}_n[\Lambda ]$
the label of a vertex
![]() $[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
. For example, let us consider a sequence of lattices
$[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
. For example, let us consider a sequence of lattices
![]() $\Lambda _0, \dots , \Lambda _n$
, where
$\Lambda _0, \dots , \Lambda _n$
, where
and
![]() $\Lambda _n:=\mathit {O} u_1\oplus \cdots \oplus \mathit {O} u_n \oplus \mathit {O} \varpi w_1\oplus \cdots \oplus \mathit {O} \varpi w_n$
. Then
$\Lambda _n:=\mathit {O} u_1\oplus \cdots \oplus \mathit {O} u_n \oplus \mathit {O} \varpi w_1\oplus \cdots \oplus \mathit {O} \varpi w_n$
. Then
![]() $\Lambda _0 \subseteq \cdots \subseteq \Lambda _n \subseteq \varpi ^{-1}\Lambda _0$
and
$\Lambda _0 \subseteq \cdots \subseteq \Lambda _n \subseteq \varpi ^{-1}\Lambda _0$
and
![]() $\varpi ^{-1}\Lambda _0$
is primitive, and since the chain
$\varpi ^{-1}\Lambda _0$
is primitive, and since the chain
![]() $\Lambda _1/\Lambda _0 \subseteq \cdots \subseteq \Lambda _n/\Lambda _0$
forms a maximal totally isotropic flag in
$\Lambda _1/\Lambda _0 \subseteq \cdots \subseteq \Lambda _n/\Lambda _0$
forms a maximal totally isotropic flag in
![]() $\varpi ^{-1}\Lambda _0/\Lambda _0$
over
$\varpi ^{-1}\Lambda _0/\Lambda _0$
over
![]() ${\mathbb F}_q$
, the corresponding homothety classes
${\mathbb F}_q$
, the corresponding homothety classes
![]() $[\Lambda _0], \dots , [\Lambda _n]$
define a chamber in
$[\Lambda _0], \dots , [\Lambda _n]$
define a chamber in
![]() ${\mathcal B}_n$
. In this case, we have that
${\mathcal B}_n$
. In this case, we have that
![]() $\mathbf {lab}_n[\Lambda _k]=2n-k \mod 2n$
for
$\mathbf {lab}_n[\Lambda _k]=2n-k \mod 2n$
for
![]() $0 \le k \le n$
. We call the chamber determined by
$0 \le k \le n$
. We call the chamber determined by
![]() $[\Lambda _0], \dots , [\Lambda _n]$
the fundamental chamber
$[\Lambda _0], \dots , [\Lambda _n]$
the fundamental chamber
![]() ${\mathcal C}_0$
. Here, we note that
${\mathcal C}_0$
. Here, we note that
![]() $\mathbf {lab}_n$
misses the values
$\mathbf {lab}_n$
misses the values
![]() $1, \dots , n-1$
in
$1, \dots , n-1$
in
![]() ${\mathbb Z}/2n {\mathbb Z}$
. It is known that
${\mathbb Z}/2n {\mathbb Z}$
. It is known that
![]() $Sp_n(F)$
acts transitively on the set of chambers [Reference GarrettGar97, Section 20.5], i.e., every chamber is of the form
$Sp_n(F)$
acts transitively on the set of chambers [Reference GarrettGar97, Section 20.5], i.e., every chamber is of the form
![]() $\gamma {\mathcal C}_0$
for
$\gamma {\mathcal C}_0$
for
![]() $\gamma \in Sp_n(F)$
. By definition, the action of
$\gamma \in Sp_n(F)$
. By definition, the action of
![]() $Sp_n(F)$
preserves the labels on
$Sp_n(F)$
preserves the labels on
![]() $\mathrm {Ver}({\mathcal B}_n)$
. It thus implies that the action is not vertex-transitive for any
$\mathrm {Ver}({\mathcal B}_n)$
. It thus implies that the action is not vertex-transitive for any
![]() $n \ge 1$
.
$n \ge 1$
.
4.3 Apartments
Let us introduce a system of apartments in the building
![]() ${\mathcal B}_n$
. See [Reference GarrettGar97, Chapter 20] and [Reference ShemanskeShe07] for basics and more details. A frame is an unordered n-tuple:
${\mathcal B}_n$
. See [Reference GarrettGar97, Chapter 20] and [Reference ShemanskeShe07] for basics and more details. A frame is an unordered n-tuple:
![]() $\{\lambda _1^1, \lambda _1^2\}$
,
$\{\lambda _1^1, \lambda _1^2\}$
,
![]() $\dots $
,
$\dots $
,
![]() $\{\lambda _n^1, \lambda _n^2\}$
, such that each
$\{\lambda _n^1, \lambda _n^2\}$
, such that each
![]() $\{\lambda _i^1, \lambda _i^2\}$
is an unordered pair of lines which span a two-dimensional symplectic subspace with the induced alternating form for
$\{\lambda _i^1, \lambda _i^2\}$
is an unordered pair of lines which span a two-dimensional symplectic subspace with the induced alternating form for
![]() $i=1, \dots , n$
, and
$i=1, \dots , n$
, and
i.e.,
![]() $\langle v, v'\rangle =0$
for all
$\langle v, v'\rangle =0$
for all
![]() $v \in V_i$
and all
$v \in V_i$
and all
![]() $v' \in V_j$
if
$v' \in V_j$
if
![]() $i \neq j$
. An apartment defined by a frame
$i \neq j$
. An apartment defined by a frame
![]() $\{\lambda _i^1, \lambda _i^2\}$
for
$\{\lambda _i^1, \lambda _i^2\}$
for
![]() $i=1, \dots , n$
is a maximal subcomplex of
$i=1, \dots , n$
is a maximal subcomplex of
![]() ${\mathcal B}_n$
on the set of vertices
${\mathcal B}_n$
on the set of vertices
![]() $[\Lambda ]$
such that
$[\Lambda ]$
such that
for some (equivalently, every) representative
![]() $\Lambda $
in the homothety class. We define a system of apartments as a maximal set of apartments.
$\Lambda $
in the homothety class. We define a system of apartments as a maximal set of apartments.
Following [Reference ShemanskeShe07], we fix a symplectic basis
![]() $\{u_1, \dots , u_n, w_1, \dots , w_n\}$
of V and a uniformizer
$\{u_1, \dots , u_n, w_1, \dots , w_n\}$
of V and a uniformizer
![]() $\varpi $
in F and lighten the notation: we denote a lattice
$\varpi $
in F and lighten the notation: we denote a lattice
by
![]() $\Lambda =(a_1, \dots , a_n; b_1, \dots , b_n)$
, and the homothety class by
$\Lambda =(a_1, \dots , a_n; b_1, \dots , b_n)$
, and the homothety class by
![]() $[\Lambda ]=[a_1, \dots , a_n; b_1, \dots , b_n]$
. For
$[\Lambda ]=[a_1, \dots , a_n; b_1, \dots , b_n]$
. For
![]() $\Lambda $
, we have
$\Lambda $
, we have
![]() $\langle \Lambda , \Lambda \rangle \subset \mathit {O}$
if and only if
$\langle \Lambda , \Lambda \rangle \subset \mathit {O}$
if and only if
![]() $\langle \varpi ^{a_i}u_i, \varpi ^{b_i}w_i\rangle =\varpi ^{a_i+b_i} \in \mathit {O}$
for all
$\langle \varpi ^{a_i}u_i, \varpi ^{b_i}w_i\rangle =\varpi ^{a_i+b_i} \in \mathit {O}$
for all
![]() $i=1, \dots , n$
. This is equivalent to that
$i=1, \dots , n$
. This is equivalent to that
![]() $a_i+b_i\ge 0$
for all
$a_i+b_i\ge 0$
for all
![]() $i=1, \dots , n$
, in which case,
$i=1, \dots , n$
, in which case,
![]() $\Lambda /\varpi \Lambda $
is a non-degenerate alternating space with the induced form over the residue field
$\Lambda /\varpi \Lambda $
is a non-degenerate alternating space with the induced form over the residue field
![]() $\mathit {O}/\varpi \mathit {O}$
if and only if
$\mathit {O}/\varpi \mathit {O}$
if and only if
![]() $a_i+b_i=0$
for all
$a_i+b_i=0$
for all
![]() $i=1, \dots , n$
.
$i=1, \dots , n$
.
For the fixed basis, let
![]() $\lambda _i^1:=F u_i$
and
$\lambda _i^1:=F u_i$
and
![]() $\lambda _i^2:=F w_i$
for
$\lambda _i^2:=F w_i$
for
![]() $i=1, \dots , n$
. The frame
$i=1, \dots , n$
. The frame
![]() $\{\lambda _i^1, \lambda _i^2\}_{i=1, \dots , n}$
determines an apartment
$\{\lambda _i^1, \lambda _i^2\}_{i=1, \dots , n}$
determines an apartment
![]() $\Sigma _0$
in the building
$\Sigma _0$
in the building
![]() ${\mathcal B}_n$
for
${\mathcal B}_n$
for
![]() $Sp_n(F)$
. We call
$Sp_n(F)$
. We call
![]() $\Sigma _0$
the fundamental apartment. The chain of lattice
$\Sigma _0$
the fundamental apartment. The chain of lattice
![]() $\Lambda _0 \subseteq \cdots \subseteq \Lambda _n$
in (4.1) defines a chamber
$\Lambda _0 \subseteq \cdots \subseteq \Lambda _n$
in (4.1) defines a chamber
![]() ${\mathcal C}_0$
in
${\mathcal C}_0$
in
![]() $\Sigma _0$
containing
$\Sigma _0$
containing
![]() $[\Lambda _0]$
. The rest of chambers in the apartment
$[\Lambda _0]$
. The rest of chambers in the apartment
![]() $\Sigma _0$
are obtained by the action of the affine Weyl group (of type
$\Sigma _0$
are obtained by the action of the affine Weyl group (of type
![]() $\widetilde C_n$
) attached to the building.
$\widetilde C_n$
) attached to the building.
Example 4.1 If
![]() $n=2$
, then we have eight chambers containing vertex
$n=2$
, then we have eight chambers containing vertex
![]() $[\Lambda _0]=[1,1;1,1]$
in a fixed apartment, where the fundamental chamber
$[\Lambda _0]=[1,1;1,1]$
in a fixed apartment, where the fundamental chamber
![]() ${\mathcal C}_0$
is defined by the chain
${\mathcal C}_0$
is defined by the chain
4.4 Special vertices and the special
 $1$
-complex
$1$
-complex
For any lattice
![]() $\Lambda $
in a symplectic space
$\Lambda $
in a symplectic space
![]() $(V, \langle \ast , \ast \rangle )$
, let us define the dual by
$(V, \langle \ast , \ast \rangle )$
, let us define the dual by
![]() $\Lambda ^\ast :=\{v \in V \mid \langle v, w\rangle \in \mathit {O} \ \text {for all }w \in \Lambda \}$
. Note that
$\Lambda ^\ast :=\{v \in V \mid \langle v, w\rangle \in \mathit {O} \ \text {for all }w \in \Lambda \}$
. Note that
![]() $\Lambda ^\ast $
is also a lattice in V. For every
$\Lambda ^\ast $
is also a lattice in V. For every
![]() $\alpha \in F^\times $
, we have that
$\alpha \in F^\times $
, we have that
![]() $(\alpha \Lambda )^\ast =\alpha ^{-1}\Lambda ^\ast $
, whence the homothety class
$(\alpha \Lambda )^\ast =\alpha ^{-1}\Lambda ^\ast $
, whence the homothety class
![]() $[\Lambda ^\ast ]$
depends only on
$[\Lambda ^\ast ]$
depends only on
![]() $[\Lambda ]$
. Let us call a vertex
$[\Lambda ]$
. Let us call a vertex
![]() $[\Lambda ]$
in the building
$[\Lambda ]$
in the building
![]() ${\mathcal B}_n$
self-dual if
${\mathcal B}_n$
self-dual if
![]() $[\Lambda ^\ast ]=[\Lambda ]$
. Below we characterize self-dual vertices in terms of labels – it is essentially proved in [Reference ShemanskeShe07, Proposition 3.1]; so we omit the proof.
$[\Lambda ^\ast ]=[\Lambda ]$
. Below we characterize self-dual vertices in terms of labels – it is essentially proved in [Reference ShemanskeShe07, Proposition 3.1]; so we omit the proof.
Lemma 4.2 Fix an integer
![]() $n \ge 1$
. For
$n \ge 1$
. For
![]() $[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
, we have that
$[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
, we have that
![]() $[\Lambda ^\ast ]=[\Lambda ]$
if and only if
$[\Lambda ^\ast ]=[\Lambda ]$
if and only if
![]() $\mathbf {lab}_n[\Lambda ]=0$
or
$\mathbf {lab}_n[\Lambda ]=0$
or
![]() $n\ \ \mod 2n$
.
$n\ \ \mod 2n$
.
For
![]() $[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
, let us call
$[\Lambda ] \in \mathrm {Ver}({\mathcal B}_n)$
, let us call
![]() $[\Lambda ]$
a special vertex if
$[\Lambda ]$
a special vertex if
![]() $[\Lambda ^\ast ]=[\Lambda ]$
. We define the special 1-complex
$[\Lambda ^\ast ]=[\Lambda ]$
. We define the special 1-complex
![]() ${\mathcal S}_n$
as a one-dimensional subcomplex of
${\mathcal S}_n$
as a one-dimensional subcomplex of
![]() ${\mathcal B}_n$
based on the set of special vertices
${\mathcal B}_n$
based on the set of special vertices
and
![]() $1$
-simplices (edges) are defined between two incident vertices in
$1$
-simplices (edges) are defined between two incident vertices in
![]() ${\mathcal B}_n$
(cf. Section 4.1): for
${\mathcal B}_n$
(cf. Section 4.1): for
![]() $[\Lambda _1]$
,
$[\Lambda _1]$
,
![]() $[\Lambda _2]$
in
$[\Lambda _2]$
in
![]() $\mathrm {Ver}({\mathcal S}_n)$
, we have
$\mathrm {Ver}({\mathcal S}_n)$
, we have
![]() $[\Lambda _1] \sim [\Lambda _2]$
if and only if there exist representatives
$[\Lambda _1] \sim [\Lambda _2]$
if and only if there exist representatives
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
from
$\Lambda _2$
from
![]() $[\Lambda _1]$
and
$[\Lambda _1]$
and
![]() $[\Lambda _2]$
, respectively, such that either
$[\Lambda _2]$
, respectively, such that either
![]() $\varpi ^{-1}\Lambda _1$
is primitive and
$\varpi ^{-1}\Lambda _1$
is primitive and
![]() $\Lambda _1 \subseteq \Lambda _2 \subseteq \varpi ^{-1}\Lambda _1$
, or the analogous relation where the roles of
$\Lambda _1 \subseteq \Lambda _2 \subseteq \varpi ^{-1}\Lambda _1$
, or the analogous relation where the roles of
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are interchanged holds. Note that since special vertices are those that are self-dual, if
$\Lambda _2$
are interchanged holds. Note that since special vertices are those that are self-dual, if
![]() $\varpi ^{-1}\Lambda _1$
is primitive, then
$\varpi ^{-1}\Lambda _1$
is primitive, then
![]() $\Lambda _2/\Lambda _1$
is a maximal totally isotropic subspace of
$\Lambda _2/\Lambda _1$
is a maximal totally isotropic subspace of
![]() $\varpi ^{-1}\Lambda _1/\Lambda _1$
over
$\varpi ^{-1}\Lambda _1/\Lambda _1$
over
![]() ${\mathbb F}_q$
. Lemma 4.2 shows that
${\mathbb F}_q$
. Lemma 4.2 shows that
![]() $[\Lambda ] \in \mathrm {Ver}({\mathcal S}_n)$
if and only if
$[\Lambda ] \in \mathrm {Ver}({\mathcal S}_n)$
if and only if
![]() $\mathbf {lab}_n[\Lambda ]=0$
or
$\mathbf {lab}_n[\Lambda ]=0$
or
![]() $n\ \ \mod 2n$
. The following proposition has been shown in [Reference ShemanskeShe07, Proposition 3.6].
$n\ \ \mod 2n$
. The following proposition has been shown in [Reference ShemanskeShe07, Proposition 3.6].
Proposition 4.3 For every integer
![]() $n \ge 1$
, the special
$n \ge 1$
, the special
![]() $1$
-complex
$1$
-complex
![]() ${\mathcal S}_n$
is connected.
${\mathcal S}_n$
is connected.
We note that
![]() $GSp_n(F)$
does not act on
$GSp_n(F)$
does not act on
![]() ${\mathcal B}_n$
through the linear transformation of lattices. Indeed, a vertex of label
${\mathcal B}_n$
through the linear transformation of lattices. Indeed, a vertex of label
![]() $2n-1\ \ \mod 2n$
in the fundamental chamber
$2n-1\ \ \mod 2n$
in the fundamental chamber
![]() ${\mathcal C}_0$
is sent by
${\mathcal C}_0$
is sent by
![]() $t_\varpi \in GSp_n(F)$
to a vertex of label
$t_\varpi \in GSp_n(F)$
to a vertex of label
![]() $n-1\ \ \mod 2n$
, which does not belong to
$n-1\ \ \mod 2n$
, which does not belong to
![]() $\mathrm {Ver}({\mathcal B}_n)$
. However, restricted on
$\mathrm {Ver}({\mathcal B}_n)$
. However, restricted on
![]() ${\mathcal S}_n$
, the group
${\mathcal S}_n$
, the group
![]() $GSp_n(F)$
acts on
$GSp_n(F)$
acts on
![]() ${\mathcal S}_n$
. Moreover, the action of
${\mathcal S}_n$
. Moreover, the action of
![]() $GSp_n(F)$
on
$GSp_n(F)$
on
![]() ${\mathcal S}_n$
is vertex-transitive since for
${\mathcal S}_n$
is vertex-transitive since for
![]() $t_\varpi =\mathrm {diag}(1, \dots , 1, \varpi , \dots , \varpi )$
in
$t_\varpi =\mathrm {diag}(1, \dots , 1, \varpi , \dots , \varpi )$
in
![]() $GSp_n(F)$
, we have that
$GSp_n(F)$
, we have that
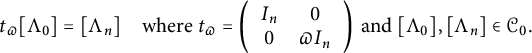 $$\begin{align*}t_\varpi[\Lambda_0]=[\Lambda_n] \quad \text{where } t_\varpi=\left( \begin{array}{cc} I_n & 0\\ 0 & \varpi I_n \end{array} \right)\ \text{and }[\Lambda_0], [\Lambda_n] \in {\mathcal C}_0. \end{align*}$$
$$\begin{align*}t_\varpi[\Lambda_0]=[\Lambda_n] \quad \text{where } t_\varpi=\left( \begin{array}{cc} I_n & 0\\ 0 & \varpi I_n \end{array} \right)\ \text{and }[\Lambda_0], [\Lambda_n] \in {\mathcal C}_0. \end{align*}$$
Note that
![]() $t_\varpi $
permutes the labels on
$t_\varpi $
permutes the labels on
![]() $\mathrm {Ver}({\mathcal S}_n)$
. This defines the action of
$\mathrm {Ver}({\mathcal S}_n)$
. This defines the action of
![]() $PGSp_n(F)$
on
$PGSp_n(F)$
on
![]() ${\mathcal S}_n$
.
${\mathcal S}_n$
.
5 Property (T) and spectral gaps
5.1 Property (T)
Let G be a topological group, and let
![]() $(\pi , {\mathcal H})$
be a unitary representation of G, where we assume that any Hilbert space
$(\pi , {\mathcal H})$
be a unitary representation of G, where we assume that any Hilbert space
![]() ${\mathcal H}$
is complex. For any compact subset Q in G, let
${\mathcal H}$
is complex. For any compact subset Q in G, let
and further let
![]() $\kappa (G, Q):=\inf \kappa (G, Q, \pi )$
, where the above infimum is taken over all equivalence classes of unitary representations
$\kappa (G, Q):=\inf \kappa (G, Q, \pi )$
, where the above infimum is taken over all equivalence classes of unitary representations
![]() $(\pi , {\mathcal H})$
without nonzero invariant vectors. We call
$(\pi , {\mathcal H})$
without nonzero invariant vectors. We call
![]() $\kappa (G, Q)$
the optimal Kazhdan constant for the pair
$\kappa (G, Q)$
the optimal Kazhdan constant for the pair
![]() $(G, Q)$
. We say that G has Property (T) if there exists a compact set Q in G such that
$(G, Q)$
. We say that G has Property (T) if there exists a compact set Q in G such that
![]() $\kappa (G, Q)>0$
. It is known that for a local field F, if
$\kappa (G, Q)>0$
. It is known that for a local field F, if
![]() $n \ge 2$
, then
$n \ge 2$
, then
![]() $Sp_n(F)$
has Property (T), while if
$Sp_n(F)$
has Property (T), while if
![]() $n=1$
, then
$n=1$
, then
![]() $Sp_1(F)=SL_2(F)$
and it fails to have Property (T) [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.5.3 and Example 1.7.4].
$Sp_1(F)=SL_2(F)$
and it fails to have Property (T) [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.5.3 and Example 1.7.4].
For any
![]() $n \ge 2$
,
$n \ge 2$
,
![]() $PSp_n(F)$
has Property (T) since
$PSp_n(F)$
has Property (T) since
![]() $Sp_n(F)$
does [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.3.4]. Similarly, for any
$Sp_n(F)$
does [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.3.4]. Similarly, for any
![]() $n \ge 2$
, the group
$n \ge 2$
, the group
![]() $PGSp_n(F)$
has Property (T) since
$PGSp_n(F)$
has Property (T) since
![]() $PGSp_n(F)/PSp_n(F)$
admits a finite invariant Borel regular measure (see Section 4.1 and [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.7.1]). (We note that for any
$PGSp_n(F)/PSp_n(F)$
admits a finite invariant Borel regular measure (see Section 4.1 and [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.7.1]). (We note that for any
![]() $n \ge 1$
, the group
$n \ge 1$
, the group
![]() $GSp_n(F)$
does not have Property (T) because it admits a surjective homomorphism onto
$GSp_n(F)$
does not have Property (T) because it admits a surjective homomorphism onto
![]() ${\mathbb Z}$
[Reference Bekka, de la Harpe and ValetteBHV08, Corollary 1.3.5].)
${\mathbb Z}$
[Reference Bekka, de la Harpe and ValetteBHV08, Corollary 1.3.5].)
We say that a subset Q of G is generating if the sub-semigroup generated by Q coincides with G. If G has Property (T) and Q is an arbitrary compact generating set of G (provided that it exists), then
![]() $\kappa (G, Q)>0$
[Reference Bekka, de la Harpe and ValetteBHV08, Proposition 1.3.2]. We will construct an appropriate compact generating set in the following.
$\kappa (G, Q)>0$
[Reference Bekka, de la Harpe and ValetteBHV08, Proposition 1.3.2]. We will construct an appropriate compact generating set in the following.
5.2 A random walk operator
In this section, fix an integer
![]() $n \ge 1$
. Recall that
$n \ge 1$
. Recall that
![]() $K=PGSp_n(\mathit {O})$
, and letting
$K=PGSp_n(\mathit {O})$
, and letting
![]() $o:=[\Lambda _0]$
, we identify K with the stabilizer of o in
$o:=[\Lambda _0]$
, we identify K with the stabilizer of o in
![]() $PGSp_n(F)$
. Let
$PGSp_n(F)$
. Let
![]() $a:=[t_\varpi ] \in PGSp_n(F)$
, and let us choose
$a:=[t_\varpi ] \in PGSp_n(F)$
, and let us choose
![]() $\xi _i \in PSp_n(F) (\subset PGSp_n(F))$
for
$\xi _i \in PSp_n(F) (\subset PGSp_n(F))$
for
![]() $i=0, 1, \dots , n+1$
such that
$i=0, 1, \dots , n+1$
such that
![]() $\xi _0:=\mathrm {id}$
and for
$\xi _0:=\mathrm {id}$
and for
![]() $i=1. \dots , n+1$
each
$i=1. \dots , n+1$
each
![]() $\xi _i$
projects onto the reflection
$\xi _i$
projects onto the reflection
![]() $s_i$
in the affine Weyl group acting on the fundamental apartment
$s_i$
in the affine Weyl group acting on the fundamental apartment
![]() $\Sigma _0$
.
$\Sigma _0$
.
Let us define a subset
![]() $\Omega :=\{k \xi _i a k', k (\xi _i a)^{-1}k' \mid k, k' \in K, i=0, \dots , n+1\}$
in
$\Omega :=\{k \xi _i a k', k (\xi _i a)^{-1}k' \mid k, k' \in K, i=0, \dots , n+1\}$
in
![]() $PGSp_n(F)$
, where we simply write
$PGSp_n(F)$
, where we simply write
Note that
![]() $\Omega $
is compact and symmetric, i.e.,
$\Omega $
is compact and symmetric, i.e.,
![]() $x \in \Omega $
if and only if
$x \in \Omega $
if and only if
![]() $x^{-1} \in \Omega $
. Let
$x^{-1} \in \Omega $
. Let
![]() $\nu $
be a Haar measure on K normalized so that
$\nu $
be a Haar measure on K normalized so that
![]() $\nu (K)=1$
. Let us define the probability measure
$\nu (K)=1$
. Let us define the probability measure
![]() $\mu $
on
$\mu $
on
![]() $PGSp_n(F)$
as the distribution of
$PGSp_n(F)$
as the distribution of
![]() $k \zeta k'$
where
$k \zeta k'$
where
![]() $k, k'$
, and
$k, k'$
, and
![]() $\zeta $
are independent and
$\zeta $
are independent and
![]() $k, k'$
are distributed according to
$k, k'$
are distributed according to
![]() $\nu $
and
$\nu $
and
![]() $\zeta $
is uniformly distributed on
$\zeta $
is uniformly distributed on
![]() $\{\xi _i a, (\xi _i a)^{-1} \mid i=0, \dots , n+1\}$
. In other words,
$\{\xi _i a, (\xi _i a)^{-1} \mid i=0, \dots , n+1\}$
. In other words,
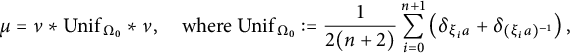 $$\begin{align*}\mu=\nu\ast \mathrm{Unif}_{\Omega_0}\ast \nu, \quad \text{where }\mathrm{Unif}_{\Omega_0}:=\frac{1}{2(n+2)}\sum_{i=0}^{n+1}\left(\delta_{\xi_i a}+\delta_{(\xi_i a)^{-1}}\right), \end{align*}$$
$$\begin{align*}\mu=\nu\ast \mathrm{Unif}_{\Omega_0}\ast \nu, \quad \text{where }\mathrm{Unif}_{\Omega_0}:=\frac{1}{2(n+2)}\sum_{i=0}^{n+1}\left(\delta_{\xi_i a}+\delta_{(\xi_i a)^{-1}}\right), \end{align*}$$
and
![]() $\delta _x$
denotes the Dirac distribution at x. We write the convolution
$\delta _x$
denotes the Dirac distribution at x. We write the convolution
![]() $\mu _1 \ast \mu _2$
for two probability measures
$\mu _1 \ast \mu _2$
for two probability measures
![]() $\mu _1, \mu _2$
on a group G. Note that the support of
$\mu _1, \mu _2$
on a group G. Note that the support of
![]() $\mu $
is
$\mu $
is
![]() $\Omega $
. If we define the probability measure
$\Omega $
. If we define the probability measure
![]() $\check \mu $
on
$\check \mu $
on
![]() $PGSp_n(F)$
as the distribution of
$PGSp_n(F)$
as the distribution of
![]() $x^{-1}$
where x has the law
$x^{-1}$
where x has the law
![]() $\mu $
, then the definition of
$\mu $
, then the definition of
![]() $\mu $
implies that
$\mu $
implies that
![]() $\check \mu =\mu $
.
$\check \mu =\mu $
.
Lemma 5.1 We have the following:
-
(1) The set
 $\Omega $
generates
$\Omega $
generates
 $PGSp_n(F)$
as a semigroup.
$PGSp_n(F)$
as a semigroup. -
(2) Fix an integer
 $n \ge 1$
. The double coset
$n \ge 1$
. The double coset
 $K \backslash \Omega /K$
is represented by a finite set
$K \backslash \Omega /K$
is represented by a finite set
 ${\Omega _0=\{\xi _i a, (\xi _i a)^{-1}, i=0, \dots , n+1\}}$
and Moreover, if
${\Omega _0=\{\xi _i a, (\xi _i a)^{-1}, i=0, \dots , n+1\}}$
and Moreover, if $$\begin{align*}\min_{K \gamma K \in K \backslash \Omega /K}\mu(K \gamma K)=\frac{1}{2(n+2)}. \end{align*}$$
$$\begin{align*}\min_{K \gamma K \in K \backslash \Omega /K}\mu(K \gamma K)=\frac{1}{2(n+2)}. \end{align*}$$
 $\gamma $
is distributed according to
$\gamma $
is distributed according to
 $\mu $
on
$\mu $
on
 $PGSp_n(F)$
, then
$PGSp_n(F)$
, then
 $\gamma o$
is uniformly distributed on the set of incident vertices to
$\gamma o$
is uniformly distributed on the set of incident vertices to
 $o=[\Lambda _0]$
in
$o=[\Lambda _0]$
in
 ${\mathcal S}_n$
.
${\mathcal S}_n$
.
Proof Let us show (1). If we let
![]() $K_0:=PSp_n(\mathit {O})$
and define
$K_0:=PSp_n(\mathit {O})$
and define
![]() $\Delta $
in
$\Delta $
in
![]() $K(=PGSp_n(\mathit {O}))$
as the image of
$K(=PGSp_n(\mathit {O}))$
as the image of
![]() $\{t_\lambda \mid \lambda \in \mathit {O}^\times \}$
, then since K contains
$\{t_\lambda \mid \lambda \in \mathit {O}^\times \}$
, then since K contains
![]() $K_0$
and
$K_0$
and
![]() $\Delta $
, and
$\Delta $
, and
![]() $\Omega $
contains
$\Omega $
contains
![]() $K\{a, a^{-1}\}K$
, the set
$K\{a, a^{-1}\}K$
, the set
![]() $\Omega \cdot \Omega $
contains
$\Omega \cdot \Omega $
contains
![]() $\bigcup _{i=1}^{n+1}K_0 \xi _i K_0$
as well as K (and thus
$\bigcup _{i=1}^{n+1}K_0 \xi _i K_0$
as well as K (and thus
![]() $K_0$
and
$K_0$
and
![]() $\Delta $
). The group
$\Delta $
). The group
![]() $K_0$
acts on the set of apartments containing
$K_0$
acts on the set of apartments containing
![]() $o=[\Lambda _0]$
transitively, and this implies that
$o=[\Lambda _0]$
transitively, and this implies that
![]() $\bigcup _{i=1}^{n+1}K_0 \xi _i K_0$
generates
$\bigcup _{i=1}^{n+1}K_0 \xi _i K_0$
generates
![]() $PSp_n(F)$
as a semigroup, which follows by looking at the induced action of reflections on apartments (cf. Section 4.3). Since the quotient
$PSp_n(F)$
as a semigroup, which follows by looking at the induced action of reflections on apartments (cf. Section 4.3). Since the quotient
![]() $PGSp_n(F)$
modulo
$PGSp_n(F)$
modulo
![]() $PSp_n(F)$
is generated by the images of
$PSp_n(F)$
is generated by the images of
![]() $\{a, a^{-1}\}$
and
$\{a, a^{-1}\}$
and
![]() $\Delta $
(cf. Section 4.1), we conclude that
$\Delta $
(cf. Section 4.1), we conclude that
![]() $\Omega $
generates
$\Omega $
generates
![]() $PGSp_n(F)$
as a semigroup.
$PGSp_n(F)$
as a semigroup.
Let us show (2). The first claim follows since
![]() $\Omega =K\Omega _0 K$
and the definition of
$\Omega =K\Omega _0 K$
and the definition of
![]() $\mu $
shows that
$\mu $
shows that
![]() $\mu $
yields the uniform distribution on
$\mu $
yields the uniform distribution on
![]() $K \backslash \Omega /K$
. Concerning the second claim, in the fundamental apartment
$K \backslash \Omega /K$
. Concerning the second claim, in the fundamental apartment
![]() $\Sigma _0$
, we note that
$\Sigma _0$
, we note that
![]() $\xi _i a o =t_\varpi o$
if
$\xi _i a o =t_\varpi o$
if
![]() $i \neq 1$
and
$i \neq 1$
and
![]() $\xi _1 a o=s_1 t_\varpi o$
, and
$\xi _1 a o=s_1 t_\varpi o$
, and
![]() $(\xi _i a)^{-1} o=t_\varpi ^{-1}o$
if
$(\xi _i a)^{-1} o=t_\varpi ^{-1}o$
if
![]() $i \neq n+1$
and
$i \neq n+1$
and
![]() $(\xi _{n+1} a)^{-1}o=s_\ast t_\varpi o$
where
$(\xi _{n+1} a)^{-1}o=s_\ast t_\varpi o$
where
![]() $s_\ast $
is a product of
$s_\ast $
is a product of
![]() $s_1, s_2, \dots , s_n$
with some repetitions; we note that such an element
$s_1, s_2, \dots , s_n$
with some repetitions; we note that such an element
![]() $s_\ast $
fixes o since it belongs to the spherical Weyl group. Furthermore,
$s_\ast $
fixes o since it belongs to the spherical Weyl group. Furthermore,
![]() $K_0(=PSp_n(\mathit {O}))$
acts on the set of apartments containing o and if we apply k whose distribution is the normalized Haar measure on
$K_0(=PSp_n(\mathit {O}))$
acts on the set of apartments containing o and if we apply k whose distribution is the normalized Haar measure on
![]() $K(=PGSp_n(\mathit {O}))$
to an incidence vertex v of o, then
$K(=PGSp_n(\mathit {O}))$
to an incidence vertex v of o, then
![]() $k v$
is uniformly distributed on the incident vertices of o. This implies the claim.
$k v$
is uniformly distributed on the incident vertices of o. This implies the claim.
For simplicity of notation, let
![]() $G:=PGSp_n(F)$
in the following discussion. Recall that
$G:=PGSp_n(F)$
in the following discussion. Recall that
![]() $\mathrm {Ver}({\mathcal S}_n)=Go$
(cf. Section 4.3). Let us denote by
$\mathrm {Ver}({\mathcal S}_n)=Go$
(cf. Section 4.3). Let us denote by
![]() $\ell ^2({\mathcal S}_n)$
the Hilbert space of square-summable complex-valued functions on
$\ell ^2({\mathcal S}_n)$
the Hilbert space of square-summable complex-valued functions on
![]() $\mathrm {Ver}({\mathcal S}_n)$
equipped with the inner product
$\mathrm {Ver}({\mathcal S}_n)$
equipped with the inner product
![]() $\langle \varphi , \psi \rangle :=\sum _{v \in \mathrm {Ver}({\mathcal S}_n)}\varphi (v)\overline {\psi (v)}$
for
$\langle \varphi , \psi \rangle :=\sum _{v \in \mathrm {Ver}({\mathcal S}_n)}\varphi (v)\overline {\psi (v)}$
for
![]() $\varphi , \psi \in \ell ^2({\mathcal S}_n)$
. Let us define an operator
$\varphi , \psi \in \ell ^2({\mathcal S}_n)$
. Let us define an operator
![]() ${\mathcal A}_\mu : \ell ^2({\mathcal S}_n) \to \ell ^2({\mathcal S}_n)$
by
${\mathcal A}_\mu : \ell ^2({\mathcal S}_n) \to \ell ^2({\mathcal S}_n)$
by
Note that
![]() ${\mathcal A}_\mu $
is well defined by the definition of
${\mathcal A}_\mu $
is well defined by the definition of
![]() $\mu $
since
$\mu $
since
![]() $\mathrm {Ver}({\mathcal S}_n)=G o$
and K is the stabilizer of o. Lemma 5.1(2) shows that
$\mathrm {Ver}({\mathcal S}_n)=G o$
and K is the stabilizer of o. Lemma 5.1(2) shows that
![]() ${\mathcal A}_\mu $
is the normalized adjacency operator on
${\mathcal A}_\mu $
is the normalized adjacency operator on
![]() ${\mathcal S}_n$
. Since
${\mathcal S}_n$
. Since
![]() $\check \mu =\mu $
, the operator
$\check \mu =\mu $
, the operator
![]() ${\mathcal A}_\mu $
is self-adjoint on
${\mathcal A}_\mu $
is self-adjoint on
![]() $\ell ^2({\mathcal S}_n)$
. Similarly, if we define
$\ell ^2({\mathcal S}_n)$
. Similarly, if we define
![]() ${\mathcal A}_{\mu ^{\ast t}}: \ell ^2({\mathcal S}_n) \to \ell ^2({\mathcal S}_n)$
in the same way with respect to the tth convolution power
${\mathcal A}_{\mu ^{\ast t}}: \ell ^2({\mathcal S}_n) \to \ell ^2({\mathcal S}_n)$
in the same way with respect to the tth convolution power
![]() $\mu ^{\ast t}$
of
$\mu ^{\ast t}$
of
![]() $\mu $
, then we have that by induction
$\mu $
, then we have that by induction
![]() ${\mathcal A}_{\mu }^t={\mathcal A}_{\mu ^{\ast t}}$
for all positive integer
${\mathcal A}_{\mu }^t={\mathcal A}_{\mu ^{\ast t}}$
for all positive integer
![]() $t \ge 1$
.
$t \ge 1$
.
Let us consider any closed subgroup
![]() $\Gamma $
of G such that
$\Gamma $
of G such that
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() ${\mathcal S}_n$
from left with a compact quotient space
${\mathcal S}_n$
from left with a compact quotient space
![]() $\Gamma \backslash {\mathcal S}_n$
, where the action is given by
$\Gamma \backslash {\mathcal S}_n$
, where the action is given by
![]() $(\gamma , v) \mapsto \gamma v$
for
$(\gamma , v) \mapsto \gamma v$
for
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $v \in {\mathcal S}_n$
. Since
$v \in {\mathcal S}_n$
. Since
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() ${\mathcal S}_n$
by simplicial automorphisms (as
${\mathcal S}_n$
by simplicial automorphisms (as
![]() $PGSp_n(F)$
does), the quotient
$PGSp_n(F)$
does), the quotient
![]() $\Gamma \backslash {\mathcal S}_n$
naturally admits a finite (unoriented) graph structure induced from
$\Gamma \backslash {\mathcal S}_n$
naturally admits a finite (unoriented) graph structure induced from
![]() ${\mathcal S}_n$
. Let us denote the finite graph by the same symbol
${\mathcal S}_n$
. Let us denote the finite graph by the same symbol
![]() $\Gamma \backslash {\mathcal S}_n$
. Note that since
$\Gamma \backslash {\mathcal S}_n$
. Note that since
![]() ${\mathcal S}_n$
is connected by Proposition 4.3, the graph
${\mathcal S}_n$
is connected by Proposition 4.3, the graph
![]() $\Gamma \backslash {\mathcal S}_n$
is connected for any such
$\Gamma \backslash {\mathcal S}_n$
is connected for any such
![]() $\Gamma $
. Here, however, we do not assume that
$\Gamma $
. Here, however, we do not assume that
![]() $\Gamma $
is torsion-free; thus, the graph
$\Gamma $
is torsion-free; thus, the graph
![]() $\Gamma \backslash {\mathcal S}_n$
may have loops and not regular. Although
$\Gamma \backslash {\mathcal S}_n$
may have loops and not regular. Although
![]() ${\mathcal S}_n$
admits a bipartite graph structure,
${\mathcal S}_n$
admits a bipartite graph structure,
![]() $\Gamma \backslash {\mathcal S}_n$
is not necessarily bipartite unless
$\Gamma \backslash {\mathcal S}_n$
is not necessarily bipartite unless
![]() $\Gamma $
factors through
$\Gamma $
factors through
![]() $PSp_n(F)$
.
$PSp_n(F)$
.
For each
![]() $v \in {\mathcal S}_n$
, let
$v \in {\mathcal S}_n$
, let
![]() $\Gamma _v:=\{\gamma \in \Gamma \mid \gamma v=v\}$
. Note that
$\Gamma _v:=\{\gamma \in \Gamma \mid \gamma v=v\}$
. Note that
![]() $\Gamma _v$
is finite and
$\Gamma _v$
is finite and
![]() $|\Gamma _v|$
is independent of the choice of representatives for
$|\Gamma _v|$
is independent of the choice of representatives for
![]() $v \in \Gamma \backslash {\mathcal S}_n$
. Let us define
$v \in \Gamma \backslash {\mathcal S}_n$
. Let us define
![]() $\ell ^2(\Gamma \backslash {\mathcal S}_n)$
the space of complex-valued functions on
$\ell ^2(\Gamma \backslash {\mathcal S}_n)$
the space of complex-valued functions on
![]() $\Gamma \backslash {\mathcal S}_n$
equipped with the inner product defined by
$\Gamma \backslash {\mathcal S}_n$
equipped with the inner product defined by
 $$\begin{align*}\langle \varphi, \psi\rangle:=\sum_{v \in \Gamma \backslash {\mathcal S}_n} \varphi(v)\overline{\psi(v)}\frac{1}{|\Gamma_{v}|} \quad \text{for }\varphi, \psi \in \ell^2(\Gamma \backslash {\mathcal S}_n). \end{align*}$$
$$\begin{align*}\langle \varphi, \psi\rangle:=\sum_{v \in \Gamma \backslash {\mathcal S}_n} \varphi(v)\overline{\psi(v)}\frac{1}{|\Gamma_{v}|} \quad \text{for }\varphi, \psi \in \ell^2(\Gamma \backslash {\mathcal S}_n). \end{align*}$$
The group
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\ell ^2({\mathcal S}_n)$
by
$\ell ^2({\mathcal S}_n)$
by
![]() $\varphi \mapsto \varphi \circ \gamma ^{-1}$
for
$\varphi \mapsto \varphi \circ \gamma ^{-1}$
for
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\varphi \in \ell ^2({\mathcal S}_n)$
, and since this
$\varphi \in \ell ^2({\mathcal S}_n)$
, and since this
![]() $\Gamma $
-action and
$\Gamma $
-action and
![]() ${\mathcal A}_\mu $
on
${\mathcal A}_\mu $
on
![]() $\ell ^2({\mathcal S}_n)$
commute, the following operator
$\ell ^2({\mathcal S}_n)$
commute, the following operator
![]() ${\mathcal A}_{\Gamma , \mu ^{\ast t}}$
on
${\mathcal A}_{\Gamma , \mu ^{\ast t}}$
on
![]() $\ell ^2(\Gamma \backslash {\mathcal S}_n)$
is well defined for all positive integer t:
$\ell ^2(\Gamma \backslash {\mathcal S}_n)$
is well defined for all positive integer t:
We have that
![]() ${\mathcal A}_{\Gamma , \mu }^t={\mathcal A}_{\Gamma , \mu ^{\ast t}}$
for all integer
${\mathcal A}_{\Gamma , \mu }^t={\mathcal A}_{\Gamma , \mu ^{\ast t}}$
for all integer
![]() $t \ge 1$
, and
$t \ge 1$
, and
![]() ${\mathcal A}_{\Gamma , \mu }$
is self-adjoint, i.e.,
${\mathcal A}_{\Gamma , \mu }$
is self-adjoint, i.e.,
![]() $\langle {\mathcal A}_{\Gamma , \mu }\varphi , \psi \rangle =\langle \varphi , {\mathcal A}_{\Gamma , \mu }\psi \rangle $
for
$\langle {\mathcal A}_{\Gamma , \mu }\varphi , \psi \rangle =\langle \varphi , {\mathcal A}_{\Gamma , \mu }\psi \rangle $
for
![]() $\varphi , \psi \in \ell ^2(\Gamma \backslash {\mathcal S}_n)$
. In other words, the operator
$\varphi , \psi \in \ell ^2(\Gamma \backslash {\mathcal S}_n)$
. In other words, the operator
![]() ${\mathcal A}_{\Gamma , \mu }$
defines a Markov chain on
${\mathcal A}_{\Gamma , \mu }$
defines a Markov chain on
![]() $\Gamma \backslash {\mathcal S}_n$
reversible with respect to the measure
$\Gamma \backslash {\mathcal S}_n$
reversible with respect to the measure
![]() $1/|\Gamma _v|$
for each vertex v.
$1/|\Gamma _v|$
for each vertex v.
5.3 Spectral gap
We normalize the Haar measure on G in such a way that K has the unit mass. Let
![]() $L^2(\Gamma \backslash G)$
denote the complex
$L^2(\Gamma \backslash G)$
denote the complex
![]() $L^2$
-space with respect to the (right) Haar measure for which each double coset
$L^2$
-space with respect to the (right) Haar measure for which each double coset
![]() $\Gamma \xi K$
has the mass
$\Gamma \xi K$
has the mass
![]() $1/|\xi ^{-1}\Gamma \xi \cap K|$
. Note that the mass coincides with
$1/|\xi ^{-1}\Gamma \xi \cap K|$
. Note that the mass coincides with
![]() $1/|\Gamma _{\xi o}|$
since
$1/|\Gamma _{\xi o}|$
since
![]() $\Gamma _{\xi o}=\Gamma \cap \xi K \xi ^{-1}$
. We consider
$\Gamma _{\xi o}=\Gamma \cap \xi K \xi ^{-1}$
. We consider
![]() $L^2(\Gamma \backslash G)^K$
the subspace of K-fixed vectors in
$L^2(\Gamma \backslash G)^K$
the subspace of K-fixed vectors in
![]() $L^2(\Gamma \backslash G)$
and naturally identify it with
$L^2(\Gamma \backslash G)$
and naturally identify it with
![]() $\ell ^2(\Gamma \backslash {\mathcal S}_n)$
(including the inner product). Let us define the unitary representation
$\ell ^2(\Gamma \backslash {\mathcal S}_n)$
(including the inner product). Let us define the unitary representation
![]() $\pi $
of G on
$\pi $
of G on
![]() $L^2(\Gamma \backslash G)$
by
$L^2(\Gamma \backslash G)$
by
Note that
![]() $\varphi \in L^2(\Gamma \backslash G)^K$
if and only if
$\varphi \in L^2(\Gamma \backslash G)^K$
if and only if
![]() $\pi (k)\varphi =\varphi $
for all
$\pi (k)\varphi =\varphi $
for all
![]() $k \in K$
.
$k \in K$
.
Let
where we recall that
![]() $\nu $
is the normalized Haar measure on K.
$\nu $
is the normalized Haar measure on K.
Lemma 5.2 For every
![]() $n \ge 1$
, and for all
$n \ge 1$
, and for all
![]() $\varphi \in L^2(\Gamma \backslash G)^K$
, we have that
$\varphi \in L^2(\Gamma \backslash G)^K$
, we have that
 $$ \begin{align*} {\mathcal A}_{\Gamma, \mu}\varphi=\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}T_\Gamma(\gamma)\varphi. \end{align*} $$
$$ \begin{align*} {\mathcal A}_{\Gamma, \mu}\varphi=\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}T_\Gamma(\gamma)\varphi. \end{align*} $$
Moreover, for all
![]() $\gamma \in \Gamma $
and for all
$\gamma \in \Gamma $
and for all
![]() $\varphi _1, \varphi _2 \in L^2(\Gamma \backslash G)^K$
, we have that
$\varphi _1, \varphi _2 \in L^2(\Gamma \backslash G)^K$
, we have that
![]() $\langle T_\Gamma (\gamma )\varphi _1, \varphi _2\rangle =\langle \pi (\gamma )\varphi _1, \varphi _2\rangle $
.
$\langle T_\Gamma (\gamma )\varphi _1, \varphi _2\rangle =\langle \pi (\gamma )\varphi _1, \varphi _2\rangle $
.
Proof Let us show the first claim. Recalling that
![]() $\mu =\nu \ast \mathrm {Unif}_{\Omega _0}\ast \nu $
, for
$\mu =\nu \ast \mathrm {Unif}_{\Omega _0}\ast \nu $
, for
![]() ${\varphi \in L^2(\Gamma \backslash G)^K}$
and
${\varphi \in L^2(\Gamma \backslash G)^K}$
and
![]() $\xi , \gamma \in G$
, we have that
$\xi , \gamma \in G$
, we have that
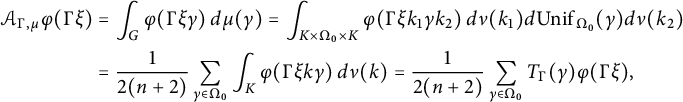 $$ \begin{align*} {\mathcal A}_{\Gamma, \mu}\varphi(\Gamma \xi) &=\int_G \varphi(\Gamma \xi\gamma)\,d\mu(\gamma) =\int_{K \times \Omega_0 \times K}\varphi(\Gamma \xi k_1 \gamma k_2)\,d\nu(k_1)d\mathrm{Unif}_{\Omega_0}(\gamma)d\nu(k_2)\\ &=\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}\int_K \varphi(\Gamma \xi k\gamma)\,d\nu(k) =\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}T_\Gamma(\gamma)\varphi(\Gamma \xi), \end{align*} $$
$$ \begin{align*} {\mathcal A}_{\Gamma, \mu}\varphi(\Gamma \xi) &=\int_G \varphi(\Gamma \xi\gamma)\,d\mu(\gamma) =\int_{K \times \Omega_0 \times K}\varphi(\Gamma \xi k_1 \gamma k_2)\,d\nu(k_1)d\mathrm{Unif}_{\Omega_0}(\gamma)d\nu(k_2)\\ &=\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}\int_K \varphi(\Gamma \xi k\gamma)\,d\nu(k) =\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}T_\Gamma(\gamma)\varphi(\Gamma \xi), \end{align*} $$
where the third equality follows since
![]() $\varphi $
is a K-fixed vector and the last identity follows from the definition of
$\varphi $
is a K-fixed vector and the last identity follows from the definition of
![]() $T_\Gamma (\gamma )$
. Hence, the first claim holds. The second claim follows from a formal computation based on the right-invariance of the Haar measure on
$T_\Gamma (\gamma )$
. Hence, the first claim holds. The second claim follows from a formal computation based on the right-invariance of the Haar measure on
![]() $\Gamma \backslash G$
, so we omit the details.
$\Gamma \backslash G$
, so we omit the details.
Let us denote by
![]() $\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
the orthogonal complement to the space of constant functions in
$\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
the orthogonal complement to the space of constant functions in
![]() $\ell ^2(\Gamma \backslash {\mathcal S}_n)$
. Note that
$\ell ^2(\Gamma \backslash {\mathcal S}_n)$
. Note that
![]() ${\mathcal A}_{\Gamma , \mu }$
acts on
${\mathcal A}_{\Gamma , \mu }$
acts on
![]() $\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
since the operator is self-adjoint. Given the right representation
$\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
since the operator is self-adjoint. Given the right representation
![]() $(\pi , L^2(\Gamma \backslash G))$
, letting
$(\pi , L^2(\Gamma \backslash G))$
, letting
![]() $L_0^2(\Gamma \backslash G)$
be the orthogonal complement to constant functions in
$L_0^2(\Gamma \backslash G)$
be the orthogonal complement to constant functions in
![]() $L^2(\Gamma \backslash G)$
, we define
$L^2(\Gamma \backslash G)$
, we define
![]() $(\pi _0, L_0^2(\Gamma \backslash G))$
by restricting
$(\pi _0, L_0^2(\Gamma \backslash G))$
by restricting
![]() $\pi $
to
$\pi $
to
![]() $L_0^2(\Gamma \backslash G)$
. The space
$L_0^2(\Gamma \backslash G)$
. The space
![]() $\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
is identified with the space of K-fixed vectors in
$\ell _0^2(\Gamma \backslash {\mathcal S}_n)$
is identified with the space of K-fixed vectors in
![]() $L_0^2(\Gamma \backslash G)$
under the identification between
$L_0^2(\Gamma \backslash G)$
under the identification between
![]() $\ell ^2(\Gamma \backslash {\mathcal S}_n)$
and
$\ell ^2(\Gamma \backslash {\mathcal S}_n)$
and
![]() $L^2(\Gamma \backslash G)^K$
. It is crucial that
$L^2(\Gamma \backslash G)^K$
. It is crucial that
![]() $\pi _0$
has no nonzero invariant vector.
$\pi _0$
has no nonzero invariant vector.
Proposition 5.3 For every
![]() $n \ge 1$
, let
$n \ge 1$
, let
![]() $\Gamma $
be a closed subgroup of
$\Gamma $
be a closed subgroup of
![]() $G=PGSp_n(F)$
such that
$G=PGSp_n(F)$
such that
![]() $\Gamma \backslash {\mathcal S}_n$
is finite. For all
$\Gamma \backslash {\mathcal S}_n$
is finite. For all
![]() $\varphi \in \ell _0^2(\Gamma \backslash {\mathcal S}_n)$
with
$\varphi \in \ell _0^2(\Gamma \backslash {\mathcal S}_n)$
with
![]() $\|\varphi \|=1$
, we have that
$\|\varphi \|=1$
, we have that
where
![]() $\kappa (G, \Omega )$
is the optimal Kazhdan constant for the pair
$\kappa (G, \Omega )$
is the optimal Kazhdan constant for the pair
![]() $(G, \Omega )$
.
$(G, \Omega )$
.
Proof For
![]() $\varphi \in \ell _0^2(\Gamma \backslash {\mathcal S}_n)$
, it follows that
$\varphi \in \ell _0^2(\Gamma \backslash {\mathcal S}_n)$
, it follows that
![]() $ \langle (I-{\mathcal A}_{\Gamma , \mu })\varphi , \varphi \rangle $
equals
$ \langle (I-{\mathcal A}_{\Gamma , \mu })\varphi , \varphi \rangle $
equals
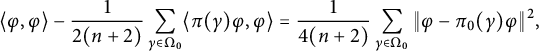 $$ \begin{align*} \langle \varphi, \varphi \rangle -\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}\langle \pi(\gamma)\varphi, \varphi\rangle =\frac{1}{4(n+2)}\sum_{\gamma \in \Omega_0}\|\varphi-\pi_0(\gamma)\varphi\|^2, \end{align*} $$
$$ \begin{align*} \langle \varphi, \varphi \rangle -\frac{1}{2(n+2)}\sum_{\gamma \in \Omega_0}\langle \pi(\gamma)\varphi, \varphi\rangle =\frac{1}{4(n+2)}\sum_{\gamma \in \Omega_0}\|\varphi-\pi_0(\gamma)\varphi\|^2, \end{align*} $$
where identifying
![]() $\varphi $
with a K-fixed vector, we have used Lemma 5.2, and the equality follows since
$\varphi $
with a K-fixed vector, we have used Lemma 5.2, and the equality follows since
![]() $\pi _0$
is the restriction of
$\pi _0$
is the restriction of
![]() $\pi $
and
$\pi $
and
and
![]() $\pi _0(\gamma )$
is unitary, and furthermore
$\pi _0(\gamma )$
is unitary, and furthermore
![]() $\gamma \in \Omega _0$
if and only if
$\gamma \in \Omega _0$
if and only if
![]() $\gamma ^{-1} \in \Omega _0$
. Moreover, we have that
$\gamma ^{-1} \in \Omega _0$
. Moreover, we have that
which follows from the first claim of Lemma 5.1(2) and since
![]() $\varphi $
is a K-fixed vector and
$\varphi $
is a K-fixed vector and
![]() $\pi _0$
is a unitary representation. Therefore, we obtain
$\pi _0$
is a unitary representation. Therefore, we obtain
Since
![]() $\pi _0$
has no nonzero invariant vector, we conclude the claim.
$\pi _0$
has no nonzero invariant vector, we conclude the claim.
Theorem 5.4 If we fix an integer
![]() $n \ge 2$
, then there exists a positive constant
$n \ge 2$
, then there exists a positive constant
![]() $c_n>0$
such that for any closed subgroup
$c_n>0$
such that for any closed subgroup
![]() $\Gamma $
in
$\Gamma $
in
![]() $PGSp_n(F)$
with finite quotient
$PGSp_n(F)$
with finite quotient
![]() $\Gamma \backslash {\mathcal S}_n$
, we have
$\Gamma \backslash {\mathcal S}_n$
, we have
![]() $\lambda _2(\Delta _{\Gamma ,\mu }) \ge c_n$
, where
$\lambda _2(\Delta _{\Gamma ,\mu }) \ge c_n$
, where
![]() $\Delta _{\Gamma , \mu }=I-{\mathcal A}_{\Gamma , \mu }$
.
$\Delta _{\Gamma , \mu }=I-{\mathcal A}_{\Gamma , \mu }$
.
Proof Since we have that
![]() $\lambda _2(\Delta _{\Gamma , \mu })=\inf _{\varphi \in \ell ^2_0(\Gamma \backslash {\mathcal S}_n), \ \|\varphi \|=1}\langle (I-{\mathcal A}_{\Gamma , \mu })\varphi , \varphi \rangle $
, Proposition 5.3 implies that
$\lambda _2(\Delta _{\Gamma , \mu })=\inf _{\varphi \in \ell ^2_0(\Gamma \backslash {\mathcal S}_n), \ \|\varphi \|=1}\langle (I-{\mathcal A}_{\Gamma , \mu })\varphi , \varphi \rangle $
, Proposition 5.3 implies that
![]() $\lambda _2(\Delta _{\Gamma , \mu }) \ge (4(n+2))^{-1}\kappa (G, \Omega )^2$
. Furthermore,
$\lambda _2(\Delta _{\Gamma , \mu }) \ge (4(n+2))^{-1}\kappa (G, \Omega )^2$
. Furthermore,
![]() $\kappa (G, \Omega )>0$
since
$\kappa (G, \Omega )>0$
since
![]() $G=PGSp_n(F)$
has Property (T) if
$G=PGSp_n(F)$
has Property (T) if
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $\Omega $
is a compact generating set of G by Lemma 5.1(1) (cf. Section 5.1). Letting
$\Omega $
is a compact generating set of G by Lemma 5.1(1) (cf. Section 5.1). Letting
![]() $c_n:=(4(n+2))^{-1}\kappa (G, \Omega )^2$
, we obtain the claim.
$c_n:=(4(n+2))^{-1}\kappa (G, \Omega )^2$
, we obtain the claim.
The proof of Theorem 1.1 now follows from Theorem 5.4 with
![]() $\Gamma $
applied to
$\Gamma $
applied to
![]() $G_g({\mathbb Z}[1/\ell ])$
modulo the center and Corollary 3.2.
$G_g({\mathbb Z}[1/\ell ])$
modulo the center and Corollary 3.2.
5.4 An explicit lower bound for the spectral gap
Appealing to the results by Oh [Reference OhOh02], we obtain explicit lower bounds for the second smallest eigenvalues of Laplacians on the graphs
![]() ${\mathcal G}^{SS}_{g}(\ell ,p)$
for
${\mathcal G}^{SS}_{g}(\ell ,p)$
for
![]() $g \ge 2$
.
$g \ge 2$
.
Corollary 5.5 For every integer
![]() $g \ge 2$
, for all primes
$g \ge 2$
, for all primes
![]() $\ell $
and p with
$\ell $
and p with
![]() $p \neq \ell $
,
$p \neq \ell $
,
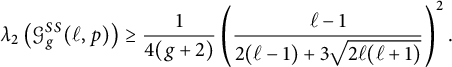 $$\begin{align*}\lambda_2\left({\mathcal G}^{SS}_{g}(\ell,p)\right) \ge \frac{1}{4(g+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2. \end{align*}$$
$$\begin{align*}\lambda_2\left({\mathcal G}^{SS}_{g}(\ell,p)\right) \ge \frac{1}{4(g+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2. \end{align*}$$
Proof We keep the notations in the preceding subsections and put
![]() $n=g$
. Let
$n=g$
. Let
![]() $F:={\mathbb Q}_\ell $
. Note that
$F:={\mathbb Q}_\ell $
. Note that
![]() $\Omega ^2$
contains K and
$\Omega ^2$
contains K and
![]() $a^2$
. The definition of the optimal Kazhdan constant shows that
$a^2$
. The definition of the optimal Kazhdan constant shows that
Furthermore, the right-hand side is at least
![]() $\kappa \left (Sp_n({\mathbb Q}_\ell ), \Omega _\ast \right )$
, where
$\kappa \left (Sp_n({\mathbb Q}_\ell ), \Omega _\ast \right )$
, where
Applying [Reference OhOh02, Theorem 8.4] to
![]() $Sp_n({\mathbb Q}_\ell )$
for
$Sp_n({\mathbb Q}_\ell )$
for
![]() $n\ge 2$
with a maximal strongly orthogonal system
$n\ge 2$
with a maximal strongly orthogonal system
![]() $\mathrm {L}$
in the case of
$\mathrm {L}$
in the case of
![]() $C_n (n \ge 2)$
[Reference OhOh02, Appendix], we have that
$C_n (n \ge 2)$
[Reference OhOh02, Appendix], we have that
 $$\begin{align*}\kappa\left(Sp_n({\mathbb Q}_\ell), \Omega_\ast\right) \ge \chi_{\mathrm{L}}(s)=\frac{\sqrt{2(1-\xi_{\mathrm{L}}(s))}}{\sqrt{2(1-\xi_{\mathrm{L}}(s))}+3}, \end{align*}$$
$$\begin{align*}\kappa\left(Sp_n({\mathbb Q}_\ell), \Omega_\ast\right) \ge \chi_{\mathrm{L}}(s)=\frac{\sqrt{2(1-\xi_{\mathrm{L}}(s))}}{\sqrt{2(1-\xi_{\mathrm{L}}(s))}+3}, \end{align*}$$
where
 $$\begin{align*}\xi_{\mathrm{L}}(s) \le \frac{2(\ell-1)+(\ell+1)}{\ell(\ell+1)}=\frac{3\ell-1}{\ell(\ell+1)}. \end{align*}$$
$$\begin{align*}\xi_{\mathrm{L}}(s) \le \frac{2(\ell-1)+(\ell+1)}{\ell(\ell+1)}=\frac{3\ell-1}{\ell(\ell+1)}. \end{align*}$$
Hence, we have for all
![]() $n \ge 2$
and all prime
$n \ge 2$
and all prime
![]() $\ell $
,
$\ell $
,
 $$\begin{align*}\kappa\left(Sp_n({\mathbb Q}_\ell), \Omega_\ast\right) \ge \frac{\sqrt{2}(\ell-1)}{\sqrt{2}(\ell-1)+3\sqrt{\ell(\ell+1)}}, \end{align*}$$
$$\begin{align*}\kappa\left(Sp_n({\mathbb Q}_\ell), \Omega_\ast\right) \ge \frac{\sqrt{2}(\ell-1)}{\sqrt{2}(\ell-1)+3\sqrt{\ell(\ell+1)}}, \end{align*}$$
and since
![]() $\kappa (G, \Omega ) \ge (1/2)\kappa (G, \Omega ^2)$
, we obtain
$\kappa (G, \Omega ) \ge (1/2)\kappa (G, \Omega ^2)$
, we obtain
 $$\begin{align*}\kappa(G, \Omega) \ge \frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}. \end{align*}$$
$$\begin{align*}\kappa(G, \Omega) \ge \frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}. \end{align*}$$
Combining the above inequality with
![]() $c_n=(4(n+2))^{-1}\kappa (G, \Omega )^2$
in the proof of Theorem 5.4, we conclude that for all
$c_n=(4(n+2))^{-1}\kappa (G, \Omega )^2$
in the proof of Theorem 5.4, we conclude that for all
![]() $n \ge 2$
and all prime
$n \ge 2$
and all prime
![]() $\ell $
,
$\ell $
,
 $$\begin{align*}\lambda_2(\Delta_{\Gamma, \mu}) \ge \frac{1}{4(n+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2. \end{align*}$$
$$\begin{align*}\lambda_2(\Delta_{\Gamma, \mu}) \ge \frac{1}{4(n+2)}\left(\frac{\ell-1}{2(\ell-1)+3\sqrt{2\ell (\ell+1)}}\right)^2. \end{align*}$$
Applying to the case when
![]() $\Gamma $
is
$\Gamma $
is
![]() $G_g({\mathbb Z}[1/\ell ])$
modulo the center together with Corollary 3.2 yields the claim.
$G_g({\mathbb Z}[1/\ell ])$
modulo the center together with Corollary 3.2 yields the claim.
Acknowledgment
We would like to thank Professors Yevgeny Zaytman and Bruce Jordan for informing us of issues in the first version of this paper and correcting references; the current version has been revised substantially since then – we greatly acknowledge them for their comments. We would also like to thank Professor Tsuyoshi Takagi for many helpful discussions and encouragement, and Professor Ken-ichi Kawarabayashi for fostering an ideal environment which made this collaboration possible.